含恒功率负载的直流微网稳定性分析

2022-06-05刘海涛徐旖旎

电力系统及其自动化学报 2022年5期

刘海涛，熊雄，徐旖旎，张海，邵瑶

（1.国网上海能源互联网研究院有限公司，上海 201210；2.中国电力科学研究院有限公司，北京 100192）

随着可再生能源和电力电子负载的发展，直流微网以其转换次数少、控制结构简单、不需要对电压的相位和频率进行跟踪等优点，成为未来家庭、楼宇和社区的主要供电架构[1]。然而，直流微网中包含恒功率负荷CPL（constant power load），电压变化时呈现负阻抗特性，极易引起母线电压振荡甚至崩溃，因此稳定性分析是直流微网研究中的核心问题之一[2]。

直流微网系统稳定性分析主要涉及静态稳定分析、小扰动稳定分析和大扰动稳定分析3个方面。静态稳定分析主要研究系统是否存在稳态工作点，是小扰动和大扰动稳定分析的基础。小扰动稳定分析则通过建立直流微网系统的小信号模型，利用Middlebrook阻抗比判据或特征值分析法对直流微网系统的局部稳定性进行分析[3-6]。前者是通过设定不同的稳定裕度和禁止区，基于阻抗比对直流微网进行小扰动稳定性分析的，其缺点是它规定了功率流向，但实际直流微电网中，有些微源如并网变换器或储能单元既可以作为电源运行也可以作为负载运行，无法明确区分电源输出阻抗和负载输入阻抗[5]。特征值分析法通过判断系统雅克比矩阵的特征值来判断系统的小扰动稳定性，其对于功率流向没有限制。文献[6]运用该方法对直流微网系统的小扰动稳定性进行了分析，得到了系统小扰动稳定的判据，并探究了系统参数对稳定性的影响，但得到的稳定判据不仅与系统参数有关，还与由系统参数决定的系统的工作点有关，因而该稳定判据不能很好的指导直流微网系统的设计。

小扰动稳定分析只能研究直流微网系统的局部稳定性，但实际直流微网中，负载突变或母线电压跌落等大扰动不可避免，因而对直流微网进行大扰动稳定分析，从全局角度评估系统稳定性十分有必要[4]。目前，较为成熟的非线性系统稳定性分析方法是李雅普诺夫直接法[7-10]。应用该方法的难点在于建立李雅普诺夫函数LF（Lyapunov function），目前已取得一些研究成果。文献[8]提出Takagi-Sugeno（TS）模糊模型的稳定性分析工具，但利用该方法需要求解线性矩阵不等式，且其个数与非线性的数目满足指数关系，因而计算比较复杂；文献[9]提出通过平方和SOS（sum-of-square）规划法构造系统的李雅普诺夫函数，但该方法是数值方法，当利用该方法分析参数对系统估计吸引域EDA（estimated domain of attraction）的影响时，参数每改变一次，就需要重新进行数值计算构造系统的LF，因而较难分析参数对EDA的影响；文献[10]提出二次对角化LF（BDQLF）法，该方法利用非线性系统的线性化矩阵构造LF，并运用遗传算法确定系统的EDA，但是遗传算法编程实现复杂，且搜索速度慢，另外遗传算法容易收敛到局部最优解，因而该方法计算复杂，EDA的保守性较强。

针对上述问题，本文从静态稳定、小扰动稳定及大扰动稳定3个方面对含CPL的直流微网系统的稳定性进行了系统性分析，主要工作包括4个方面：①建立了直流微网系统的等效降阶数学模型，并通过仿真软件Matlab/Simulink对该等效降阶模型的有效性进行了验证；②分析了直流微网系统存在静态工作点的条件，得到系统静态稳定的判据，并在此基础上，利用李雅普诺夫稳定性第一定理，得到了直流微网系统的小扰动稳定判据，为直流微电网系统的设计提供参考依据；③利用混合势函数理论并结合LaSalle不变集定理得到了系统小扰动稳定平衡点的EDA；④对所得稳定性判据和EDA进行仿真验证，证明了其正确性。

1 直流微网结构与数学模型

1.1 直流微网结构

直流微网系统通常包含储能单元ES（energy storage）、分布式发电单元DGs（distributed generations）、并网变换器单元和负载单元等[5]。其中：储能单元具有平衡功率的作用，可作为恒功率单元或电源运行，作为电源运行时源变换器采用电压-电流下垂控制方式平衡母线电压；DGs通常由再生能源构成，为最大限度利用可再生能源并考虑其波动性和间歇性，DGs常采用最大功率跟踪控制策略，可看作CPL；并网变换器单元作为直流微电网与电网的接口可作为CPL运行或电源运行；负载单元包括直接接入母线的负载和通过变换器接入母线的负载，后者可看作CPL。本文选择储能单元作为电源，通过源变换器接入母线；恒功率单元由荷变换器连接可变电阻来表示，系统的具体结构如图1所示，详细系统参数见表1。

图1 直流微网系统的拓扑结构Fig.1 Topological structure of DC microgrid system

表1 直流微网系统的参数Tab.1 Parameters of DC microgrid system

1.2 直流微网的等效降阶模型和模型验证

忽略图1中源、荷变换器的电压电流控制动态，则图1左侧可等效为理想电压源串电阻电路，右侧可等效为CPL。因而图1中的系统结构可以简化为如图2所示的等效电路模型，图中：P为DGs、并网变换器单元和负载单元中CPL的功率之和；RL和Ld分别是线路电阻和电感，C是母线电容，R是负荷电阻，I是电感电流，V是电容电压，Rk和Vref是源变换器电压-电流下垂控制的下垂系数和参考电压。

图2 直流微网系统等效电路模型Fig.2 Equivalent circuit model of DC microgrid system

根据图2所示，以I和V为状态变量，系统的非线性降阶数学模型可表示为

式中，Rd=Rk+RL。

式（1）即为本文分析的直流微网系统的等效降阶数学模型。为验证其正确性，在Matlab/Simulink中分别搭建如图1所示的开关模型和等效降阶数学模型，并做仿真验证。

运行工况：t=3 s时功率P由300 W阶跃到500 W，仿真结果如图3所示。由图3可见，暂态过程中，开关模型和本文所提的降阶数学模型具有较好的拟合度，说明该降阶数学模型可以较好地反映系统的暂态特性，验证了降阶数学模型的正确性。

图3 基于开关模型和数值模型的仿真结果对比Fig.3 Comparison of simulation result between switch model and numerical model

2 稳定性分析

直流微网系统的稳定性分析可分为3个步骤。

步骤1 静态稳定分析。分析系统是否存在平衡点。

步骤2 小扰动稳定分析。分析系统的平衡点是否为小扰动稳定平衡点SEP（stable equilibrium point）。

步骤3 大扰动稳定分析。分析系统经受大扰动后的暂态过程的稳定性。

需要强调的是，上述步骤中，系统静态稳定是进行步骤2的前提，系统小扰动稳定是进行步骤3的前提。

2.1 静态稳定分析

系统的平衡点满足系统状态变量的导数等于0，故令式（1）左边等于0，得系统的平衡点ei=[Ii,Vi]，其中Ii是系统第i个平衡点的电感电流分量，Vi是系统第i个平衡点的电容电压分量。则有

基于式（2）可知，系统静态稳定的充要条件为

将式（3）中小于号右侧式子记作P1。

由上述分析可知，功率P小于P1时系统存在2个平衡点，系统静态稳定。

2.2 小扰动稳定分析

由李亚普诺夫稳定性第一法可知，如果系统平衡点的雅克比矩阵特征值的实部皆小于0，则该平衡点是小扰动稳定的[3]。本文利用该定理分析直流微网系统的平衡点e1和e1是否为SEP，或者在什么条件下是SEP，即系统小扰动稳定的判据。

对式（1）线性化，各平衡点的雅可比矩阵为

对于式（4），矩阵J(ei)的特征特征值λ1、λ2的实部小于0与λ1+λ2＜0且λ1λ2＞0等价。而λ1+λ2等于J(ei)的迹tr(J(ei))，λ1λ2等于J(ei)的行列式。因而可得

2.2.1 平衡点e1的小扰动稳定性

将式（2）的e1代入式（4）可得J(e1)，求其行列式得

2.2.2 平衡点e2的小扰动稳定性

将式（2）的e2代入式（4）可得J(e2)，求其行列式得

电容C取不同值所对应的2种情况讨论tr(J(e2))与0的大小关系。

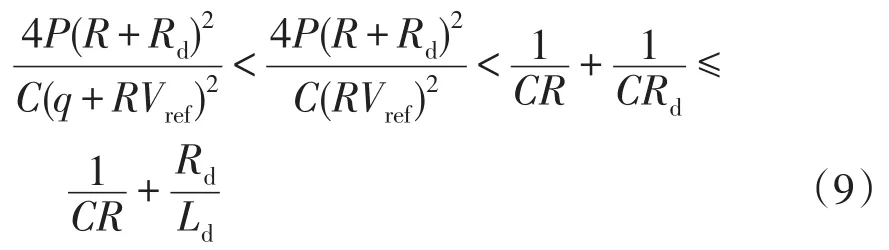
将式（10）小于号右侧式子记作P2。

图4 小扰动稳定分析示意Fig.4 Schematic of small disturbance stability analysis

2.3 基于混合势函数法的大扰动稳定分析

本文将在系统小扰动稳定的基础上，利用混合势函数理论并结合LaSalle不变集定理给出直流微网系统小扰动稳定平衡点的估计EDA。

2.3.1 混合势函数理论

Brayton和Moser基于基尔霍夫定律证明了对于非线性电路可以描述[11-12]为

式中：I为电感电流；V为电容电压；L和C分别为电路中电感和电容组成的对角矩阵；P(x)为混合势函数MPF（mixed potential function）的标量函数。文献[11]给出MPF的一般形式为

结合式（1）可得MPT对时间的导数为

由式（13）可知，如果电路中只有电感或电容，则-P（x）或P（x）对时间的导数小于0。这种情况可以运用李雅普诺夫稳定性定理判断系统的稳定性。但通常情况下，电路中电感和电容是同时存在的，故P（x）对时间的导数不定[11]。为了解决这一问题，Brayton和Moser在R和LC中至少存在1类线性元件的假设下，给出了3种构造李雅普诺夫型能量函数LEF（Lyapunov-type energy function）的方法和3条相应的稳定性定理。其中第1、2条稳定性定理要求R线性，第3条稳定性定理则要求LC线性。本文分析系统的电感和电容是线性的，满足第3条稳定性定理的假设条件，故本文运用该条定理分析直流微网系统的大扰动稳定性，为方便下文应用，现重述如下[11]。

2.3.2 直流微网系统的MPF和LEF

选择Γ的起始点和终点分别为图2系统的稳态工作点(Ie,Ve)和任意点(I,V)。由于MPF与积分路径无关，因而本文选取电流的方向作为积分路径，因而直流微网系统的MPF为

式中：Ipe为CPL的稳态电流；等号右侧各项依次为Rd、R、CPL和等效电压源的电流势函数以及电容支路的电压和电流的乘积。化简式（15）可得

结合式（14）和式（16）可得直流微网系统的LEF为

由μ1+μ2＞0可得到

将式（18）大于号右边的式子记作Vmin。

由MPT理论的第3条稳定性定理可知，当μ1+μ2＞0时，dF(I,V)/dt＜0成立。结合式（18）可知，当V＞Vmin时，dF(I,V)/dt＜0成立。

2.3.3 直流微网系统的估计吸引域

由上文分析可知，当V＞Vmin时，dF(I,V)/dt＜0成立，但F(I,V)的正定性仍不确定。不过LaSalle不变集定理并不要求F(I,V)正定，故本文运用该定理刻画直流微网系统的EDA。LaSalle不变集定理介绍如下[13]。

（2）在Ωl内，所有x满足dV(x)/dt＜0。则Ωl内所有使得dV(x)/dt=0的点的集合叫做K，M是K内的最大不变集。如果系统的初始点位于Ωl内，那么随着t→∞，系统一定收敛于M中的点。

图5 LEF的三维图和二维等高线图Fig.5 Three-dimensional plot and two-dimensional contour of LEF

根据图5中LEF的等高线在状态空间中围成的区域随LEF值的变化趋势，结合LaSalle不变集定理可得直流微电网系统的EDA为

根据式（19），可得直流微网系统的EDA如图6所示。EDA的含义是：如果系统的初始点在其内，则随着t→∞系统一定收敛于xe。此外，为验证该EDA的正确性，本文利用文献[4]中的逆轨迹法，直流微网系统的真实吸引域边界如图6所示。由图可见，该EDA在系统真实的吸引域边界内，这说明本文所刻画的EDA是正确的。此外图6中灰色区域为利用MPT理论刻画的EDA的保守性对应的区域。

图6 直流微网系统的吸引域和EDAFig.6 Domain of attraction and EDA of DC microgrid system

3 仿真分析

为验证本文分析得到的静态稳定判据（3），小扰动稳定判据式（9）和式（10）以及系统EDA式（18）的正确性，借助Matlab/Simulink对工况1～3进行仿真，如无特殊说明系统参数与表1保持一致。

图7 工况1的仿真结果Fig.7 Simulation results under working condition 1

图8 工况2的仿真结果Fig.8 Simulation results under working condition 2

图9 工况3的仿真结果Fig.9 Simulation results under working condition 3

对于工况1，从图7（b）和7（c）所示的仿真结果中可以看出，当P小幅阶跃但小于P1时，系统稳定。但是P小幅阶跃超过P1时，系统失稳。该仿真结果验证了判据（3）和判据（9）的正确性。

对于工况2，由图8（b）和8（c）可以看出，当P小于P2时，功率小幅阶跃，系统都是稳定的。此外，t=34 s时P阶跃到890 W，此时P与P2非常接近，系统等幅振荡。当t=42 s时，P小幅阶跃超过P2，系统振荡失稳。该仿真结果验证了判据式（10）的正确性。

对于工况3，由图9（b）和9（c）中的实线可知，P由8.0 kW阶跃到8.7 kW然后再阶跃到8.9 kW时，系统稳定。说明P为8.0、8.7和8.9 kW时，系统都是小扰动稳定的。但是，功率P直接由8.0 kW阶跃到8.9 kW，如图虚线所示，系统失稳，因此图9（b）和9（c）呈现的失稳现象无法通过小扰动稳定分析解释。然而，通过构建系统平衡点的EDA能够很好地解释该失稳现象，为便于下述分析，定义P=8.0、8.7和8.9 kW时，系统的SEP分别为xs1、xs2和xs3。

图10展示了P=8.7 kW与P=8.9 kW对应的SEP的EDA（Ω2与Ω3）和工况3对应的系统相轨迹。由图10可见，P=8.0 kW对应的SEP(xs1)在Ω2内、P=8.7 kW对应的SEP(xs2)在Ω3内，因而由李雅普诺夫稳定性定理可知，P由8.0 kW阶跃到8.7 kW然后再阶跃到8.9 kW对应的暂态过程必然暂态稳定，这与图9（b）和9（c）的仿真结果一致。此外，由图10可见，xs1在Ω3外，这说明P直接由8.0 kW阶跃到8.9 kW时，系统有可能暂态失稳，这也解释了图9（b）和9（c）中P直接由 8.0 kW 阶跃到8.9 kW时，系统失稳的原因。