基于回归学习与特征挖掘的运行风险评估

王天昊 ，马世乾 ，宋海涛 ，赵士朗 ，于光耀

（1.国网天津市电力公司电力科学研究院，天津 300384；2.天津市电力物联网企业重点实验室，天津 300384；3.国网天津市电力公司，天津 300010）

现代电力系统集成了监控和数据采集SCADA（supervisory control and data acquisition）以及相量测量单元PMU（phasor measurement unit）等设备数据采集系统。在给电力系统的运行与控制提供更多电力系统信息的同时，这些海量数据也对电力系统数据处理的实时性与数据挖掘能力提出了更高要求。现代电力系统的规模和复杂度逐渐升高，传统基于模型的方法的建模难度与求解模型难度也随之提升；现代电力系统更多运行在接近极限的情况下[1]，系统在扰动和异动的运行状况下面临更高的风险。鉴于现代电力系统的以上表现，有必要寻求一种充分利用电力系统数据信息来快速精准地建立实时风险评估与提供超前风险预警的方法[2]。

机器学习与数据挖掘相比于建立系统模型的求解方式，将更具计算快速性、计算鲁棒性以及对于噪声数据的相对不敏感性[3]。

运行风险评估基于对预想事故状态下系统的状态分析，重点关注威胁系统稳定安全运行的电压越限、线路过载等不安全因素，从而采取切削负荷的方式来保证安全运行。因此，风险评估需要对电力系统N在N-1N-2系统条件的大量非线性潮流方程进行逐一离线求解，计算量很大。而对于现代电力系统，特别是考虑可再生能源具有的高度随机性，系统的运行状态在短时间内可能经历多种运行状态的变化，这就对系统运行风险的评估速度提出了更高要求。

当前，对于电网风险评估的思路可以分为两大类，即基于模型驱动的风险评估和基于数据驱动的风险评估。模型驱动的风险评估方法通常包括系统状态生成、系统状态评估、可靠性指标计算等主要步骤，其中，系统状态生成通常采用蒙特卡洛模拟法和状态枚举法[4]，但无论是状态枚举法还是蒙特卡洛法，均需要对大量系统故障状态进行分析计算，才能得到满足精度要求的风险指标，其计算效率偏低，很难满足在线要求。系统状态生成之后，需要对每一个系统状态进行迭代式的最优潮流分析；最后，在风险指标计算环节，通过定量计算失负荷风险指标以准确度量系统的实际运行风险水平。但是，由于系统的复杂性和庞大性，风险指标目前无法由单一指标进行表征，如何准确建立反映系统或元件的各类风险指标，以及在多个侧面建立科学且全面的风险指标体系，需要更加深入的探讨和研究。综上所述，模型驱动的风险评估方法是目前主流思路，国内外对模型驱动的电力系统风险评估技术已有了深入讨论，但现有方法难以快速处理风险评估所需的庞大系统状态集，难以满足在线应用的实时性要求。

Rocco教授等[5]首先进行了将机器学习运用到动态运行条件下的风险评估的尝试，结果表明仅利用状态空间的一小部分可以在允许的误差范围内实现对系统的风险评估。文献[6]采用自适应支持向量机法结合蒙特卡洛模拟对设备故障概率进行学习预测，文中提出一种依据信息性强弱顺序的自适应策略提高学习效率，对于非线性高维的风险水平计算有很大潜力。文献[7]全面讨论了贝叶斯网络BN（Bayesian network）在风险评估中的应用现状以及未来可能。从BN网络，到加入时间要素的动态贝叶斯网络DBN（dynamic Bayesian network）用以预测，以及面向对象的BN网络OOBN（object oriented Bayesian network）建立类和对象的关联，便于含相似组成的复杂网络分层重用简单模型以提升效率。因此，数据驱动的运行风险评估方法被提出，它通过采用机器学习等技术改善系统状态生成或加速系统状态评估环节，以提升运行可靠性评估的计算效率。

利用数据驱动可在一定程度上弥补状态生成阶段的建模缺陷。对于元件状态的建模以及对于系统供求不确定性的建模，传统上都是基于元件长时间内的平均概率，实时准确性差；在状态生成阶段使用数据驱动方法能够以生成的状态为基础借助机器学习进行启发式抽样。在系统状态生成阶段使用数据驱动有如下主要思路：提取典型故障数据完善故障模型、利用机器识别加快蒙特卡洛模拟的效率，提升状态生成环节的效果。

在对于元件/系统状态的更准确模拟方面，多采用机器学习机制分析历史数据提取故障概率模型[8]，评估对象包括输电线[9-10]、变压器[11]等关键设备以对整体系统进行风险评估。文献[12]基于气象、设备、地理多源异构信息建立适于台风天气下输电杆塔的风险评估。

在状态分类加速模拟过程方面，使用SVM与蒙特卡洛模拟相结合的方法进行风险评估的探索起步很早，研究成果相对丰富。文献[13]基于SVM方法并以雅可比切分量作为向量机学习的目标用于电压稳定性的表示与评估，但风险水平的考察方面较为单一，缺少对于线路等其他影响因素的考虑。更完整地，文献[11]利用最小二乘支持向量机LSSVM（least squares support vector machine）与拉丁超立方蒙特卡洛抽样法实现了较为完整的风险评估过程。而利用SVM可分类的特性可获得超平面将系统状态划分为运行态与故障态，而后只需针对故障态使用潮流分析进而计算系统风险情况便可省去样本中大量的成功运行样本的状态计算用时。普通SVM适合小样本训练，而LSSVM法进一步将问题线性化降低求解难度，从而取得大规模适用性，其实现系统风险评估的速度能克服系统规模的影响[11]。

使用数据驱动的评估不必像模型驱动那样对迭代寻优有极大依赖，而对于状态的最优潮流求解与迭代是导致风险评估耗时的一大主要原因，因此依靠机器训练来代替繁杂重复的寻优任务有望加速其进程。

在系统状态评估计算加速方面，文献[14]以元件可靠性参数为输入，使用改进的BP算法训练人工神经网路最终得到实际实现的负荷数据并以此确定负荷削减策略以完成对发输电组合系统的可靠性评估。依靠对人工神经网络的训练解决了传统可靠性评估中最为耗时的最优潮流确定环节；综合能源系统有融合新能源协同发展的势头，文献[15]提出了借助堆栈降噪自编码器建立了电-气综合能源系统的概率能流模型挖掘多能流高阶特征，为综合能源系统研究提供分析工具。

在数据需求方面，上述研究需要的电气量类型众多，涉及混合同步与非同步数据，故对PMU设备数量提出更高需求。另一方面，电力大数据中数据冗余[16]、数据异常[17]等问题威胁着数据驱动方法准确性与效率的来源。因此本文考虑PMU设备在主要站点布设与提供的特点，挖掘特征数据以避免冗余PMU的设备投入及数据关联性分析异常的问题。

本文在回归型支持向量机SVR（support vector regression）基础上提出一种挖掘运行状态数据与风险指标的关联分析方法，并借助智能算法完善参数配置提升效果，融合模型驱动法完善历史数据覆盖不足的缺陷，建立“离线建模-在线评估”的风险评估新模式。结果显示该方法在保证评估精度的前提下提升风险评估效率，满足实时要求。

1 基于数据特征挖掘的回归模型

1.1 回归型支持向量机模型

SVR是用于解决回归型学习任务问题的模型，其功能是将l维输入向量xi映射到实值的输出yi。为了拟合任意的函数关系，需要建立非线性的SVR模型，其数学关系可以表述为

式中：w和b分别为权值和偏置，可以基于现有的数据集进行最优化拟合来确定；h(xi)为非线性映射关系。对于ε-SV回归问题，学习目标是建立输入输出向量之间尽可能平滑的函数映射关系y=f(x)，使得实际输出y与目标输出ŷ的误差在误差边界ε的范围内。所建立函数的平滑性能够保证模型不会出现过拟合的问题，便对权重的欧几里得范数提出了最小化的要求，对于向上向下的偏差则分别建立松弛变量来考虑。因此，回归模型的学习目标可以转化为优化模型，即

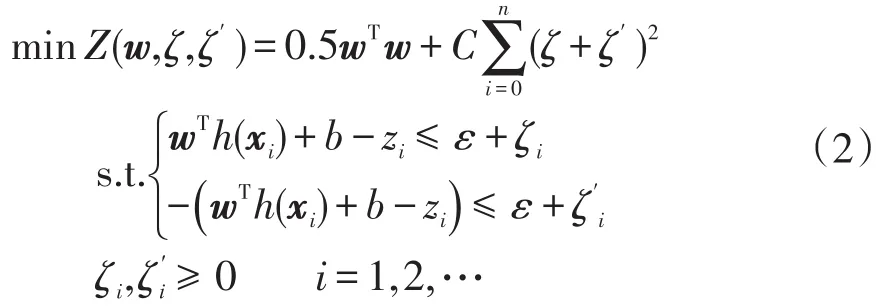
式中：C为与经验误差与泛化误差有关的罚系数；zi为每个样本对应的目标函数值；ε为误差容限；ζ、ζi为松弛变量。通过拉格朗日乘子建立对偶问题求解上述优化问题，得到的函数映射为

因此，决定回归效果的关键参数为核参数γ，误差容限ε以及罚因子C。对于这些参数的优选对于网络展现的效果极为关键，k(xi,xj)为指数部分对应的核函数，用于参数优选的蚁群算法。

1.2 特征选择模型

对于回归型学习任务，最为重要的是把握数据特征。对于电力系统而言，信息采集系统和潮流运算前后所涉及的电气量数目种类繁多，其中一部分电气量之间具有高度相关关系，还有一部分数据是冗余的。而过多数据组成的高维数据输入将降低数据挖掘的能力，也对神经网络的学习性能提出了更高要求，因此有必要采取特征提取技术首先对数据输入进行降维。特征提取虽然属于一种降维方式，但相比于其他降维方法，可通过选择现有特征的子集而非应用数据变换来实现。因此，对于具有n个特征的特征集，特征提取的方式是从中提取出规模为m的特征子集来使目标函数最小化。对于电力系统而言，不同维度特征的降维算法不适用于电力系统的风险评估，因为系统中的PMU装置通常安装在变电站和发电厂位置，一般的改变维度特征进行变化的降维法仍然需要在所有的n个节点设置信息采集装置，而特征提取的方法则只需要选取其中的m个节点来获取必要的特征信息。

因此，特征提取一方面要保证神经网络的表现效果，另一方面应提取出尽可能少的特征数量，属于双目标优化的问题，所以本文采用多目标粒子群优化来进行特征选择。

优化的目标函数为

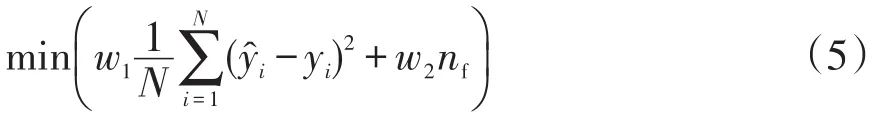
式中：N为样本数量；w1、w2为分配权重；̂为目标输出值，通过求解最优潮流方程得到；y为实际输出；函数括号内第一大项表示函数的均方误差；nf为特征集中的特征个数。同时待优化的函数也可以作为适应度函数来评判所提取的特征组合的结果。由于PMU装置安装在发电厂和主要变电站处，根据其能够提供的数据信息，选择的原始输入为发电机节点的有功出力、电压幅值、电压相角以及源于历史负荷曲线的用能需求。

1.3 基于改进蚁群算法的回归模型参数优化

本文提出了一种蚁群优化ACO（ant colony optimization）已经被用于调整超参数建立拟合问题，ACO能够处理寻找可变问题组件的最佳组合或排列，并被提议用于解决组合优化问题，从而服务于在线应用。使用蚁群算法的优化目标函数为

蚁群算法中，每个蚂蚁个体所在的位置坐标都对应一个参数取值组合，因此以上述目标函数作为个体的适应度函数。

蚁群的历史位置将影响后续蚂蚁个体对于位置的选择，这种影响方式可以理解为蚂蚁之间传递信息的“信息素”。蚂蚁在其所在坐标上留下信息，信息素浓度更高的地点将更吸引后续的蚂蚁，因此具有影响个体选择的更高权重wi。传统蚁群算法用于解决离散点路径寻优，构建的解也是离散解，概率分布是离散型的，因而不适用于本文参数寻优问题。参数对应的蚂蚁位置坐标可以在一个连续立方空间内任何处，所以选用连续高斯核函数来表示蚁群的概率分布。高斯核函数能够表示成为n个蚂蚁个体的一维高斯概率密度函数gi(x)的加权和，即

对于本文的参数优化问题，有3个参数有待搜索，所以问题维度为3，对于每个维度都对应一个不同的高斯核函数，即G1、G2、G3。权重wi可以按照高斯函数计算为

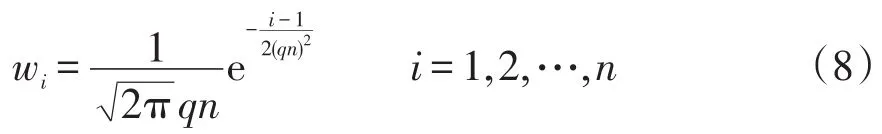
式中：i为蚂蚁在蚁群中个体适应度的排名；n为种群规模，对同一蚁群来说，n为定值；q为强化因子；qn表示高斯函数的标准差，随着其数值增大，蚁群位置的选择将从集中于当前最优解向逐渐更均匀的分布状态变化。由式（8）可见，排名靠前的蚂蚁按照高斯密度求得的被选择概率更高，因此权重wi随排名位次i的增加而递减，q则直接影响着蚁群中蚂蚁个体的权重wi离散情况。

本文提出了将权重与历史最优位置相关联的方法，也就是在所有出现过的适应度排序中具有最佳适应度位置处设置一只静止的虚拟蚂蚁，即0号蚂蚁，在种群中虚拟蚂蚁始终保持最高的适应度，因此其他蚂蚁名次则顺延一位。按照本文改进的蚁群规则，历史最优能够被保留而不会损失，权重便能够与历史最优建立关联，而不再是与当前个体中最优值关联，这种修改能够进一步加快对于最优参数选择的求解速度。

因此，改进的蚁群算法需要考虑0号蚂蚁，高斯概率函数的权表示为

蚂蚁将在一定的概率下选择新的位置。原始方法中，产生的新解用于修改信息素表，但在本文连续空间的寻优计算中，则用于动态地生成概率密度函数。因此，新蚁群的产生规则为

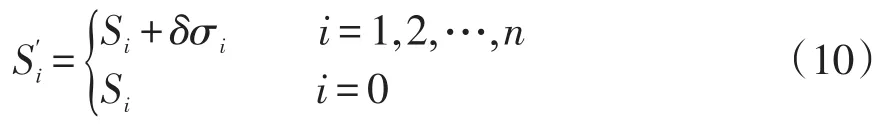
式中：Si和Sj分别为蚂蚁个体i与个体j的位置系数；η为信息素的损失。经过多次更新后，蚂蚁的信息素会逐渐吸引彼此相互靠近，蚁群分布将缩减在一定的小范围之内，对应参数的最优取值范围；而所产生的历史最优个体将作为参数的最优取值。应用蚁群算法优选参数的步骤如下。

步骤1 首先对蚁群进行随机初始化，即随机确定参数的取值。确定蚁群算法所使用的相关参数，包括信息素损失系数、蚁群规模等。

步骤2 根据每一个蚂蚁个体的坐标建立使用相应参数的回归模型，并计算固定训练次数后的误差，从而对当前蚁群进行适应度评估，记录历史最优适应度个体。

步骤3 判断蚁群历史最优适应度是否达到允许的拟合误差限。若不满足，则按照高斯概率模型更新蚁群，回到步骤2；若满足，则蚁群算法停止，以历史最优适应度个体作为参数的最优取值。

2 支持向量回归挖掘系统风险特征

电力系统风险评估需要考虑各种可能出现的系统状态。由于现代电力系统的高可靠性特点，系统的历史运行数据中难以涵盖众多小概率的运行状况，而这些小概率事件却可能对系统运行有极高的风险与隐患，对于风险评估环节不可或缺，因此本文提出了一种基于离线建模仿真的方法用以提供给必要的训练数据。为了进一步降低数据采集的硬件成本，节省PMU单元与数据内存，提高训练过程对于数据特征的敏感度，预先采用多目标粒子群算法对于系统数据进行了数据特征挖掘。同时，本文的混合方法还采用了改进的蚁群算法对回归学习模型进行参数调优，从而加快模型训练并使得运行状态到系统风险的关联映射更准确，提升表现精度。离线-在线混合运行风险评估算法流程如图1所示，步骤如下。

图1 离线-在线混合运行风险评估算法流程Fig.1 Flow chart of offline-online assessment algorithm for operation risk

步骤1 输入系统设备停运等参数，建立系统不确定因素概率模型，依据概率模型进行系统状态抽样。

步骤2 对系统状态逐一进行最优潮流计算，以负荷损失作为风险评价指标，存储为对应状态的数据标签。

步骤3 依据系统风险水平将数据分为有风险、无风险的两类，并从每一类中提取等量的数据，再按照7：3的比例重新分配为测试数据集与训练数据集，从而使得每个数据集中的有风险状态数量与无风险状态数量大致相当。

步骤4 以拟合误差和特征数量最小为目标，建立多目标粒子群法对输入特征进行选择。根据原始特征维度建立超立方体空间，粒子在立方体顶点之间移动。

步骤5 为每一个粒子建立使用相同参数和训练次数的回归模型，以拟合误差和粒子与原点距离评价粒子和群的适应度。

步骤6 计算单个粒子的个体最优位置和群体最优位置，计算相应权重，并更新粒子群，直到迭代次数达到上限。取最优粒子的坐标输出，由于坐标向量中元素取值为0或者1，所以坐标对应了决定特征选择与否的状态向量。

步骤7 特征选择的输出向量与数据集输入向量作向量点乘运算，形成特征测试集与特征训练集备用。

步骤8 以最小化拟合误差为目标，通过改进蚁群算法为回归向量机选择参数γ、C、ε最适取值组合，首先设定蚁群算法的种群规模、信息素损失系数等。

步骤9 在连续的立方体空间内随机生成蚁群，蚂蚁的坐标对应参数的连续取值，为每个蚂蚁建立回归训练模型，使用特征数据集进行训练，并以拟合误差评价蚁群适应度，计算选择权重决定选择概率并更新蚁群位置，更新历史最优个体，优势个体取代等量劣势个体，保证蚁群规模不变。直到群体的拟合误差达到设定标准，此时蚁群因为彼此的信息素相互吸引而分布范围缩小，形成了参数取值的较优范围。

步骤10 结合训练模型的关键参数建立回归向量机模型，使用特征筛选后的模型驱动获取的数据输入回归模型进行一次离线训练，即可快速建立系统运行状态与风险的关联关系。

步骤11 在线应用阶段，对系统运行状态进行特征筛选并输入复用网络即可获取相应状态下的风险水平。

3 算例分析

在IEEE-RTS79系统上进行测试，考虑了发电机故障对系统电能出力的影响以及用户用能特性随时间的变化，因此形成了系统的大量场景。该系统包括了24个节点、32台发电机组、38条支路，峰值负荷为2 850 MW。其中，38条支路包括5台变压器支路、1条电缆支路和32条输电支路组成。

通过改进蚁群算法计算所得的最优的核参数与学习率分别为1.34与0.132，使用多目标粒子群算法选出的特征向量为57，约占输入数据的46%，年负荷损失量（MW·h/a）和负载损失概率被用作衡量电力系统可靠性的指标。表1给出了第2节所提混合方法在IEEE-RTS-79系统上的应用结果，并与传统基于蒙特卡洛抽样的模型驱动方法进行对比，以MCS传统方法作为数据基准衡量所提方法的精度。

表1 计及源荷不确定性的算例系统运行风险评估结果Tab.1 Assessment result of operation risk of the example system considering uncertainties in source and load

表1展示了本文计及电力系统时变运行状态的算例系统运行风险计算方法的实现效果。结果显示负荷损失指标与失负荷概率指标相比于MCS计算所得的标准结果，相对误差均小于3%。表示该方法能保持计算精度，同时相比传统只有离线建模分析的风险评估方法，其计算时间降低了3个数量级，能够对电力系统实时变化的运行状态提供即时的风险信息反馈。图2和图3分别是该系统的节点年负荷削减期望水平和全系统在不同场景下的年负荷削减期望水平（MW·h/a），表明本文所提出的方法不仅可以提供当前运行状态下全系统的风险指标，而且能反映每个用能节点的风险水平。

图2 算例系统负荷节点运行风险评估结果Fig.2 Assessment result of operation risk of load buses in the example system

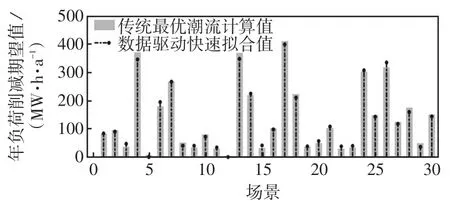
图3 算例系统运行风险评估结果Fig.3 Assessment result of operation risk of the example system

4 结 语

本文提出一种基于数据特征挖掘与回归型机器学习的离线建模-在线驱动的电力系统运行风险评估方法。测试结果显示，该方法在保持原有计算精度的基础上，相比传统的风险评估方法的计算时间从24 min缩减到不足2 s，适于对电力系统实时运行状态提供风险反馈；本文提出的数据特征挖掘方法，不仅降低系统对PMU量测设备的数量要求，同时节省训练时间；本文以降低拟合误差为优化目标，特别提出改进蚁群算法，来进行SVR模型的参数优选，改善对风险关联函数的拟合效果。基于离线训练，该方法建立的风险关联函数适用于电力系统当前结构下存在电能供需变化的相关运行情景，尚不包括运行时线路故障导致的电力系统拓扑结构变化情况，未来将进一步解决数据驱动运行风险评估相关的拓扑感知问题。