基于VMD-PSO-多核极限学习机的短期负荷预测

2022-06-05吴松梅蒋建东燕跃豪

电力系统及其自动化学报 2022年5期

吴松梅，蒋建东，燕跃豪，鲍薇

（1.郑州大学电气工程学院，郑州 450000；2.国网河南省电力公司郑州供电公司，郑州 450000）

负荷预测是电力系统的运行调度的关键环节，也是实现电网安全经济运行和科学管理的重要依据[1]。因此，提高负荷预测的精度对电力系统具有重大意义。

目前，用于电力系统短期负荷预测的方法主要有传统方法和现代方法两类，其中：传统方法主要有卡尔曼滤波法、回归分析法、趋势外推法和时间序列法等[2-4]，传统预测方法对历史数据要求严格，无法在处理大量数据的情况下建立变量之间良好的非线性关系，因此，难以得到准确的预测结果；现代预测方法主要有人工神经网络和支持向量机等[5-8]，随着人工神经网络的普及，越来越多的研究人员使用人工神经网络进行负荷预测。文献[9]提出了一种极限学习机ELM（extreme learning machine）算法；文献[10]将该算法应用于负荷预测证实了该算法的有效性。但ELM网络的输入权值和隐含层的阈值是随机设定的，且合适的隐含层数量难以确定。针对上述问题，文献[11]将核极限学习机KELM（kernel extreme learning machine）应用于风功率预测，由于KELM引入核函数，从而无需设定隐含层数量和输入权值参数，有效解决了随机映射对建模的影响，大大提高了预测精度。但是KELM在应用的过程中通常采用单一核函数，难以适应多种数据特征的样本[12]。近年来，为提高负荷预测的精度，大量学者将目光集中在组合预测模型上。文献[13]通过经验模态分解EMD（empirical mode decom-position）技术将用户侧微电网负荷分解为多个模态分量，然后对不同的模态分量进行预测；文献[14]对负荷进行小波分解WD（wavelet decomposition），并采用不同的模型对分解后的分量进行预测。这两种技术的使用均提高了负荷预测的精度，但WD对阈值选择敏感，EMD存在模态混叠问题。文献[15]采用的变分模态分解VMD（variational modal decomposition）技术对噪声具有良好的鲁棒性，在设置合理的收敛条件下，相对于EMD分解的模态函数个数较少，降低了建模的复杂度。

针对KELM单一核函数难以适应样本多数据特征的问题，本文通过将多种核函数加权构成多核极限学习机MKELM（multi-kernel extreme learning machine）从而加强模型的回归精度。并通过组合模型，将原始的负荷序列采用VMD分解为规律性更好的子序列，对模型中混合核函数的众多参数采用PSO算法寻优得到最优参数。采用Matlab仿真实验验证了本文所提出的组合算法模型具有更好的回归精度和泛化能力。

1 变分模态分解

VMD技术是Dragomiretskiy等在2014年提出的一种信号分解方法，相对于WMD和WD，VMD能够更好地还原原始信号，具有更好的噪声鲁棒性。使用该方法可以将波动信号分解为K个不同频段的本征模态函数的子信号。

（1）使用VMD进行K阶分解时，可以将其看作约束变分问题，则有

（2）引入增广拉格朗日函数，求解上述约束变分问题的最优解，得

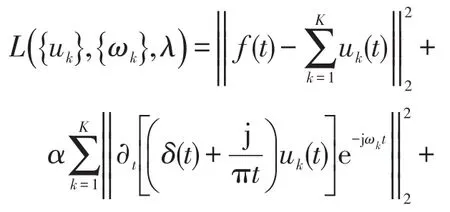
式中：α为二次惩罚因子，用于降低高斯噪声的干扰；λ为拉格朗日乘子。使用乘子交替方向法来求解上述增广拉格朗日函数及式（1）约束变分问题最优解。

（3）最终得VMD的更新过程为

对于给定的判别精度ε＞0，若满足

则VMD收敛，停止更新。

2 多核极限学习机

KELM模型在ELM模型的基础上，以核映射代替随机映射，将低纬度空间的问题转化到完备的内积空间解决，大大降低了网络的复杂度，使得回归问题的预测能力更强，泛化能力更好[16]。但是不同核函数的预测性能在相同的样本上都存在较大的差异[17]，这意味着标准KELM算法中的单一核函数难以适应多样性的负荷样本，为此，本文将KELM进行改进，提出一种多核函数的核极限学习机，得到MKELM模型，以克服核极限学习机的缺陷，解决回归能力不足的问题。

对于样本集(xi,ti),i=1,2,…,n，标准的KELM的输出为

式中：K(x,xi)核函数；KELM为核矩阵；I和T分别为对角矩阵和目标向量矩阵；C为正则化系数，C越大模型精度越高，C越小泛化能力越强，合适的C值对模型而言至关重要。

由式（7）知，当核函数K(x,xi)确定时，即可得到预测结果，因此，K(x,xi)的选取是模型预测精度的关键。核函数的类型可分为全局核和局部核，常见的核函数有Poly核、RBF核、Lin核[17-18]，其核函数形式分别为

式中：σ、c1为RBF核的核参数；d为Poly核的核参数。

将上述核函数相加，构成混合核函数，即

式中，c2、c3、c4为各个核函数的加权系数，其取值范围为[0，1]，且满足的约束条件为

将式（8）～式10）和式（12）代入式（11），得

将式（13）代入式（7）即可得到MKELM模型。该模型中的混合核函数结合了全局核和局部核的优点，使其在不同参数下不仅有良好的局部搜索能力，同时也加强了全局搜索能力。由于多核函数参数较多，人工确定参数效率低下，采用PSO算法对MKELM中的6个参数c1、c2、c3、σ、d、C进行优化。

3 基于VMD-PSO-MKELM的短期负荷预测

电力负荷由于人类活动、天气等众多因素，呈现出非线性和不确定性的特点，但人类的生产生活是有规律性的，所以负荷也存在显著的周期性。为准确分析负荷的特性，采用VMD将负荷分解为具有更高规律性的IMF模态，为每个模态建立MKELM模型，并采用PSO算法为每个模型进行优化处理得到最优解，最后将每个IMF模态的预测结果进行加权求和得到最终的预测结果。

基于VMD-PSO-MKELM模型算法具体可分为数据预处理及初始化阶段、PSO阶段和MKELM预测阶段，各个阶段具体的工作流程如图1所示。

图1 VMD-PSO-MKELM预测模型流程Fig.1 Flow chart of VMD-PSO-MKELM prediction model

3.1 数据预处理及初始化

（1）将原始负荷代入上述VMD过程，将天气、日类型以及分解后的负荷序列构成若干的输入样本，有

式中：1≤k≤K；Pk为分解后的第k个负荷序列；W代表天气；D为日类型。

（2）数据归一化。由于输入样本中包含负荷、温度和日类型，为避免各种输入数据的单位和大小不一样而影响预测结果，需要同时消除量纲，加速算法寻优过程，因此对数据采用归一化处理。归一化公式为

（3）将归一化数据划分为训练集和测试集。

3.2 PSO阶段

（1）初始化粒子群：设定种群大小为20，迭代次数为100，初始寻优时和寻优结束时的权重ωstart和ωend分别为0.9和0.4，粒子的速度及位置范围分别在[-1，1]和[-5，5]之间更新。

（2）采用PSO算法的MKELM相关参数，使用训练样本对MKELM进行训练并得到粒子的适应度，其计算公式为

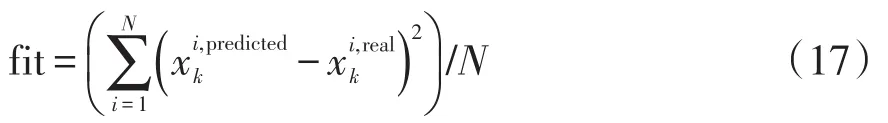
（3）更新MKELM参数，直至满足适应度或最大迭代次数，得到MKELM最优参数。

3.3 MKELM预测阶段

（1）将最优参数和数据预处理得到的测试样本代入MKELM模型，然后计算训练集核矩阵、输出权重和测试集核矩阵，进而将测试集核矩阵和输出权重求积得到每种模态的预测结果，最后对K种模态的结果加权求和，得到负荷预测结果为

（2）结果评估。为评估VMD-PSO-MKELM组合算法模型的性能，采用百分误差PE（percentage error）、平均绝对值百分误差MAPE（mean absolute percentage error）以及均方根误差RMSE（root mean squared error）3项指标，分别表示为

式中，xreal为负荷真实值。

4 算例分析

通过对某城市电网2012年负荷的预测，验证VMD-PSO-MKELM组合算法模型的有效性。将VMD分解后各种IMF模态分别建立PSO算法优化的MKELM算法模型，对1月1日—5月29日的数据进行模型训练，对5月30日的负荷进行预测。为了充分考虑负荷的周期性和相同类型日的相似性，将相同类型日同一时刻的负荷也作为模型的输入，因此本文模型的输入变量共9个，分别为：上周同一日类型和前一天相同时刻及上一时刻的负荷、最高最低温度以及类型日。本文中分别建立5种负荷预测模型：BP、ELM、KELM、MKELM以及VMDPSO-MKELM，其中KELM模型中的核函数采用RBF核函数，并对每种预测模型的性能进行分析。

4.1 VMD分解结果

实验样本为某城市2012年采集的负荷序列，数据采样间隔为15 min，选取其中1月1日—5月30日的样本进行负荷预测实验。采用VMD技术对原负荷序列进行分解，部分负荷分解结果如图2所示。其中VMD参数分别设置为：二次惩罚因子α=2 000、初始中心频率ω=0、收敛判据e=10-7、分解阶数经过反复试验最终选定为K=4。

图2 原始负荷序列及VMD分解结果Fig.2 Original load sequence and VMD decomposition results

从图2中可以看出，IMF1分量不具备周期性，平均振幅较大，变化缓慢。IMF2分量具备良好的周期性，容易掌握其规律性，IMF3和IMF4分量振幅较小，波动较大。

4.2 寻优结果

对上述的IMF1～IMF4分别建立PSO-MKELM算法模型，其适应度函数如图3所示，可以看出，IMF1和IMF2在前25代的寻优过程中，适应度急剧下降，在25代左右找到最佳适应度，之后的适应度基本保持不变；相对于IMF3和IMF4在80代和60代以后适应度保持不变，IMF1和IMF2的寻优过程更迅速，这是由于分解的子序列中IMF2相对于IMF3和IMF4的规律性更好，而IMF1的波动性较小。

图3 各子序列适应度变化过程Fig.3 Changing process of fitness of each subsequence

对不同模态的负荷子序列分别建立PSOMKELM模型，经PSO优化后各子序列的MKELM参数如表1所示。

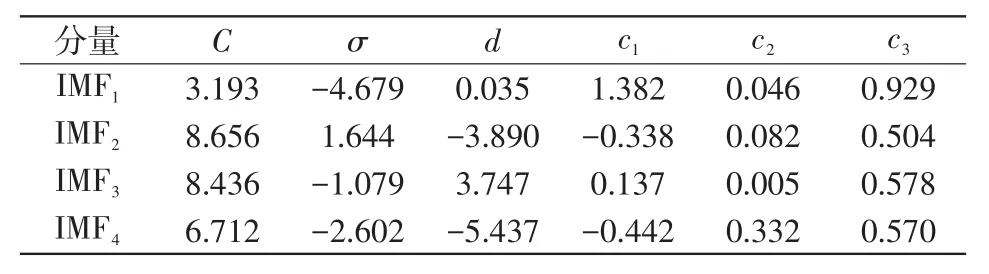
表1 各子序列模型参数Tab.1 Model parameters of each subsequence

4.3 结果对比

分别建立BP网络、ELM、KELM和MKELM预测模型，设定BP网络隐含层数量为15、目标误差为0.001、学习效率为0.01、迭代次数为2 000。ELM模型相对于BP网络具有更好的学习速率和泛化能力且收敛速度更快，设定其隐含层数量为25。KELM模型参数正则化系数为10、RBF核函数参数σ为2。MKELM模型参数正则化系数为10、混合核函数的系数分别为0.4、0.4、0.2，混合核函数的参数c1、σ和d均设置为2。不同模型的预测结果及误差如图4和图5所示。

由图4可见，本文所提VMD-PSO-MKELM组合算法模型的预测结果更贴近真实值，具有更好的预测精度。相对于单核极限学习机，多核极限学习机的预测结果更准确，因此MKELM模型将KELM模型中的核函数混合之后，不仅有良好的局部搜索能力，同时也加强了全局搜索能力，从而能够取得更精确的预测结果。

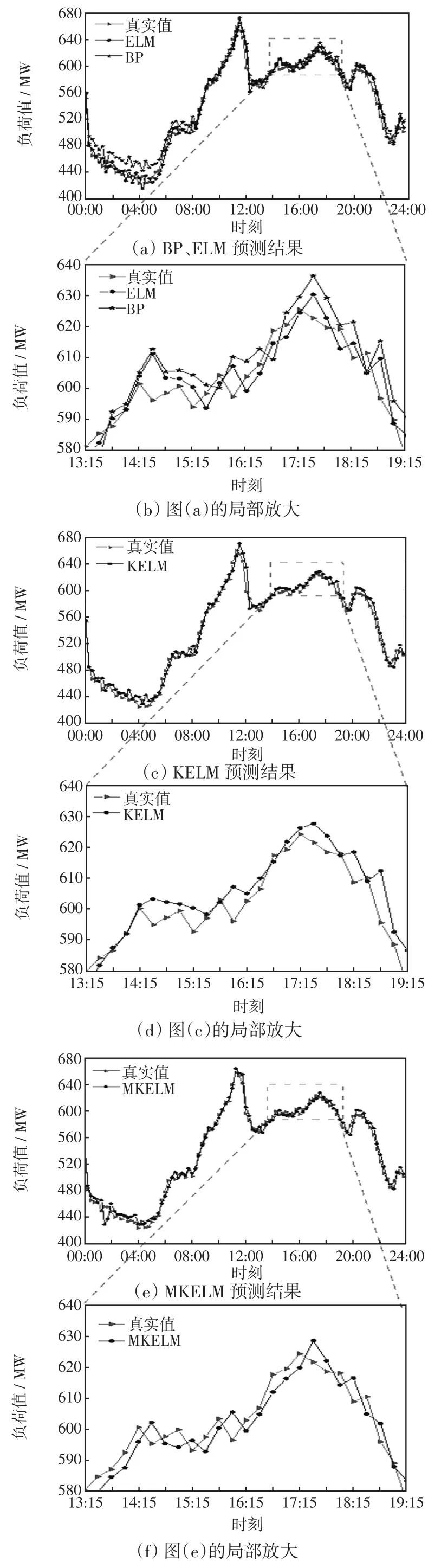
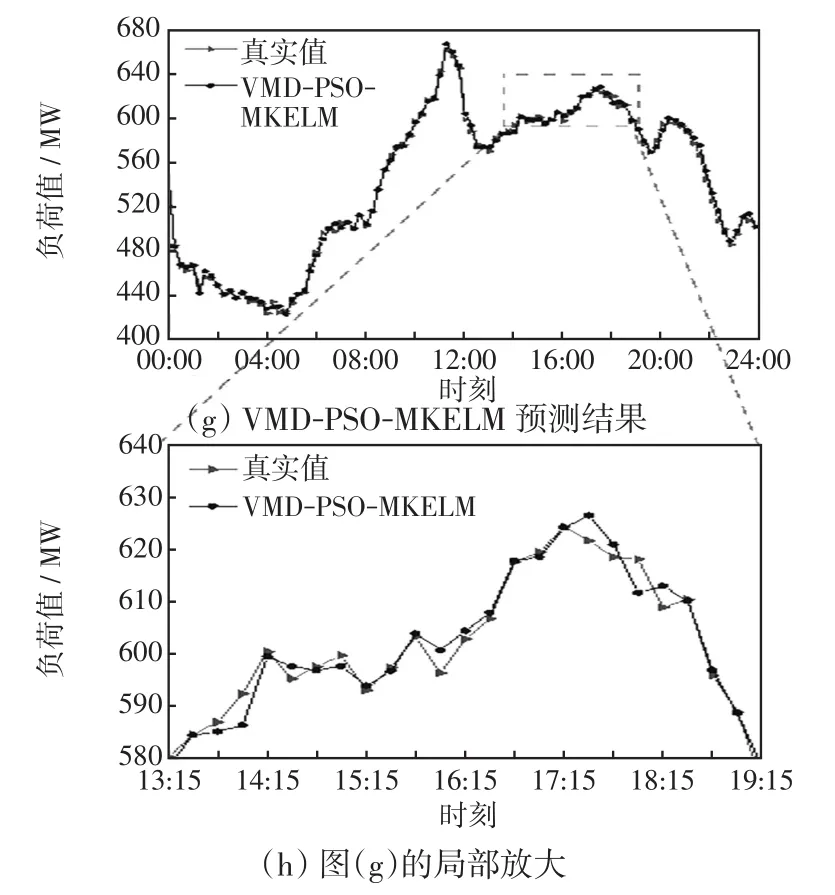
图4 不同模型预测结果对比Fig.4 Comparison of prediction results among different models

由图5可见，负荷在尖峰处容易出现误差较大的情况，在最大值处尤为显著，预测效果不够理想，而使用VMD技术将负荷分解后，上述情况得到有效改善。经VMD分解后的IMF模态大部分具有明显的规律性，而剩下部分的振幅较小。此时对不同的IMF模态训练，得到的模型能够更好地适应各个模态，得到更加准确的预测结果。

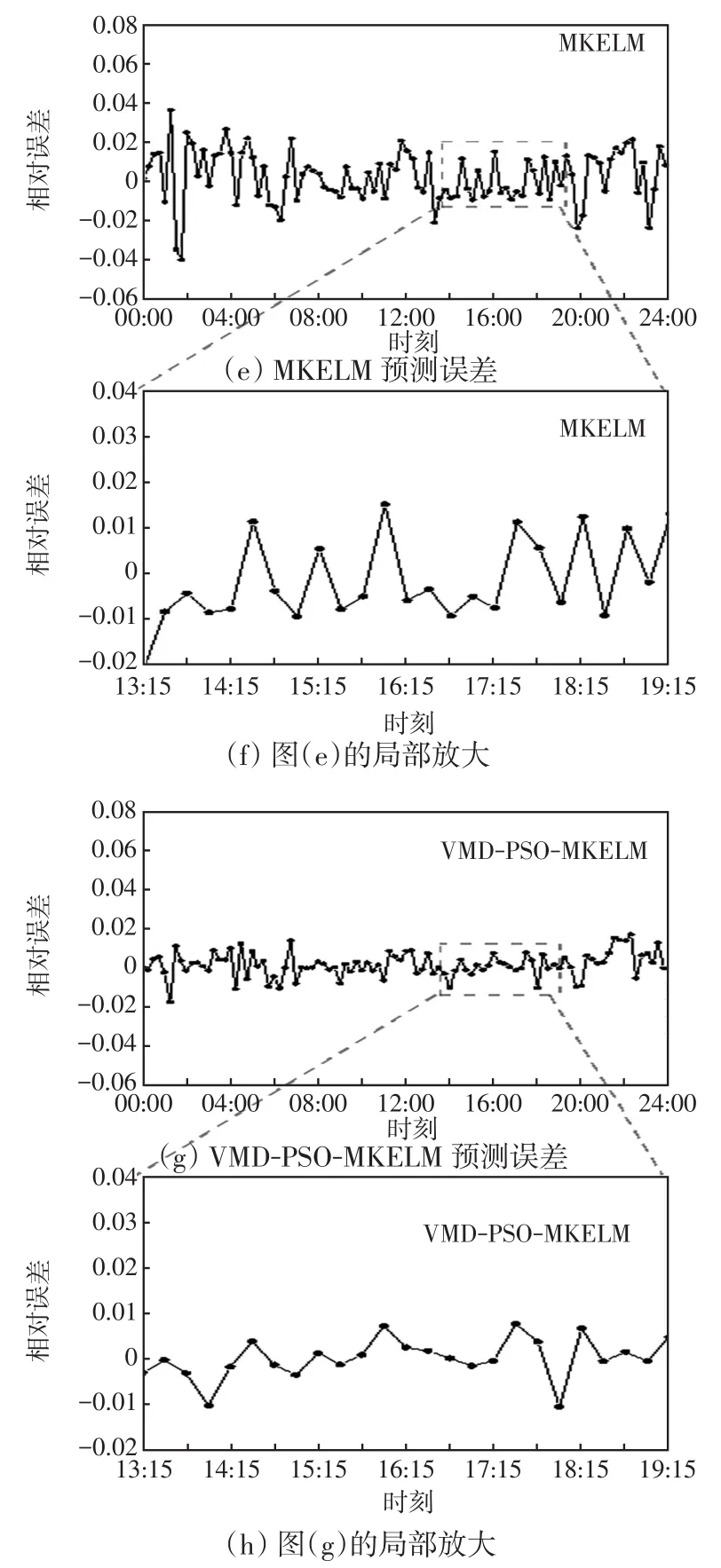
图5 不同模型误差对比Fig.5 Comparison of error among different models

为了验证本模型的适应能力，采用VMD-PSOMKELM组合算法模型，分别对6月1日和7月1日进行负荷预测，误差结果如图6所示，可见其误差范围在±3%，满足电力调度对负荷预测精度的要求。其中6月1日和7月1日的MAPE和RMSE参数分别为0.749 6%、6.127 5 MW和1.283 3%、8.446 9 MW。观察7月1日的预测误差，其中2%～3%的误差占比为3.125%，±1%～±2%的误差占比为23.958%，-1%～1%的误差占比为72.917%，再次证明本模型不仅有良好的预测能力，同时也具有较强的适应能力，能够针对不同日期的数据做出准确的预测。

图6 6月1日和7月1日负荷预测误差Fig.6 Load forecasting errors on June 1 and July 1

为验证VMD技术对预测精度的影响，分别构建VMD-BP、VMD-ELM和VMD-KELM组合模型进行电力负荷的预测。分别与BP、ELM和KELM模型对比，每种模型均进行10次预测，并采用式（20）和式（21）对上述预测结果进行评价，结果如表2所示。相对于单一的BP、ELM、KELM模型，组合模型的预测精度均有不同程度的提高，MAPE指标分别提高了14.24%、15.26%和16.67%，RMSE指标分别提高了12.87%、13.84%和15.93%。

表2 预测效果对比Tab.2 Comparison of prediction effect

由表2中各种模型的对比结果可知，MKELM算法模型明显优于KELM、ELM和BP算法模型，其MAPE指标相对于KELM、ELM和BP算法模型分别提高了6.50%、7.32%、26.03%，而RMSE指标分别提高了5.19%、6.57%、20.93%。而经过VMD分解和PSO算法优化后的MKELM组合算法模型各项指标均为最优，相对于MKELM算法，MAPE指标和RMSE指标分别提高了17.58%和16.96%，说明VMD-PSO-MKELM组合算法模型的预测精度更好。