基于热力传导的Cartogram算法研究

胡碧菡 李连营

1武汉大学资源与环境科学学院，湖北武汉，430079

地理信息可视化分为点数据可视化、线数据可视化、区域数据可视化［1］。传统方法中，每个地图区域显示一个与实际陆地面积成比例的区域，有时可能严重歪曲人口统计数据，在人口专题地图中，人口密集的城市应该比人口稀少的大城市得到更多关注度。Cartogram解决了这个问题，它按照属性数据的比例重新分配区域面积，对地图进行适当扭曲变形，同时保持各个区域单元的邻接关系。虽然会在一定程度上改变实际区域的面积和轮廓，但是能更加直观地表达该区域的属性数据信息。

在过去，数学、计算机科学和物理领域的GIS科学家和研究人员在用计算机制作Cartogram时，开发出了一系列高效的Cartogram地图绘制算法。为了减少角度的变形，Tobler［2，3］开始了计算机自动绘制Cartogram的第一步，但是这种方法在某些情况下可能会产生地图的重叠，从而破坏地图的拓扑结构。为了提高计算速度，Dougenik等［4］引入了一种“细胞”算法，该算法比Tobler算法快，但仍然不能排除拓扑错误。Gusein⁃Zade等［5］完全去除了单元格，使用一个连续的“位移场”来测量地图上每个点的位移。Dorling［6］提出了基于细胞自动机的方法，该方法在每次迭代中识别接近区域边界的细胞，并进行重新分配。此算法十分简单，但是生成的Cartogram十分扭曲，不易阅读。现在最常用、最权威的方法是基于扩散密度均衡的算法［7］，该算法能保留原来区域间的拓扑关系，但计算效率不高。针对此问题，本文提出一种基于热力传导的Cartogram算法。

1 传统基于扩散密度均衡的Cartogram生成算法

根据特定人口密度绘制地图的方法允许人口以某种方式从高密度地区流动到低密度地区，直到各地的人口密度均衡。即基础物理学的线性扩散过程［8］是传统基于扩散方法的基础。

从概念上讲，这种基于扩散密度均衡的算法在进行不同分辨率转换时，会产生不同的格网尺寸、扩散格网尺寸、迭代次数及生成时间，转换质量越高，生成Cartogram所需的时间越长。为此，需要优化算法。

2 基于热力传导的Cartogram生成算法

在基于热力传导的Cartogram算法中，人口密度ρ不仅是位置r(x，y)的函数，也是时间t的函数。在一个密度均衡的投影中，时间趋于无穷时，人口密度必须接近均值，即所有的x、y必须满足：

式中，为时间趋于无穷时的均衡密度。即粒子必须以热力扩散的方式传导，不同密度区域中的所有初始密度差异随着时间推移而完全消除，然而仅通过这种基于热力扩散的方式还不能定义投影T，必须要知道每个点(x，y)在t时刻被热流拖动的速率v(x，y，t)。因为在流动过程中没有热力源，所以v必须满足质量守恒方程，即连续方程：

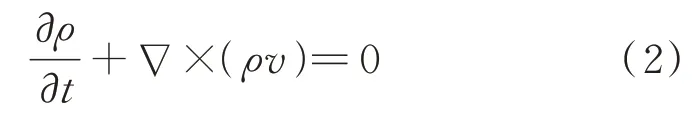
式中，∇为拉普拉斯算子。

如果已知所有的(x，y，t)对应的v(x，y，t)，就可以通过r(0)计算出r(t)：

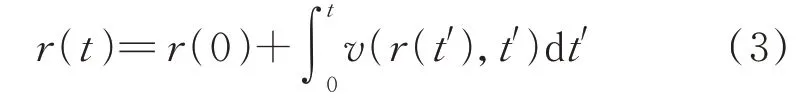
投影T是将r(0)移动到t趋于无穷的r(t)的函数。

扩散方程需要同时满足菲克定律和连续方程，将菲克定律代入连续方程后，由式（2）可知，密度ρ由扩散方程控制，这是基于扩散的Cartogram生成算法背后的关键因素，菲克扩散的一个优点是不会产生可能导致投影T严重变形的涡流。菲克扩散并不是独一无二的能保持质量守恒且无涡流产生的扩散过程，本文为了探寻其他无涡流且能保持质量守恒的制图算法，使用密度区域平均的线型均衡的方法来代替之前的扩散方程。

对所有坐标进行仿射变换后，把地图区域置于一 个边界为xmin=0，xmax=Lx，ymin=0，ymax=Ly（Lx、Ly表示矩形框边界坐标）的矩形框中，规定粒子不能流出矩形框范围内，t≤1内的速度可以用正弦和余弦的傅里叶变换来表示。

用Lx Ly的矩形网格覆盖地图，在计算开始时，使用快速傅里叶变换算法来对地图上的各坐标点进行变换［9］。这个过程在总运算时间中所占的比例可以忽略不计，将Lx Ly傅里叶变换储存在存储器中，用基本微分算法在每个网格点r处得到v(r，t)。在此基础上，求出方程中的被积函数。使用预测校正法数值逼近积分，自动适应下一个时间步长的大小，在每个步骤中，将每个Lx Ly集成体直接分配给不同的处理单元。因此，可以通过多核处理器并行计算。

与传统基于扩散密度均衡的Cartogram生成算法相比，该方法有以下特点：①多线程处理。多个处理单元同时工作，从而大大减少计算时间。②积分与时间t无关。傅里叶变换只需要在计算开始时进行一次，并且后续只需要简单的加减乘除运算，大大提高了运算速度。③传统基于扩散的算法需要连续迭代计算直至t趋于无穷大，而本文算法只需要计算到t=1的时刻，这样就不需要再检查积分是否收敛，并可以从不同起点开始积分，大大减少计算时间。

该方法的计算效率和图形精度在理论上都有很大提高。为了检验该结论，本文用经典的美国总统大选数据和印度国内生产总值数据来进行实验与分析。

3 实验与分析

本文实验环境为Mac Book Air，配置为Intel Core i5处理器，1.6 GHz双核，8 GB运行内存，256 GB固态盘（solid state disk，SSD），采用C语言实现Cartogram算法。

本文用2016年美国选举投票结果及2015年印度国内生产总值（gross domestic product，GDP）数据进行实验分析。图1（a）、图1（b）分别是2016年美国选举投票结果基于传统扩散方法和基于热力传导的算法生成的Cartogram。两者宏观上无可识别性差别，但是生成图1（b）所需要的时间仅为生成图1（a）所需时间的1/10。

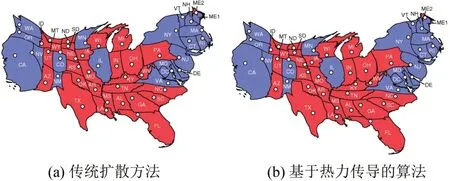
图1 2016美国选举投票结果CartogramFig.1 Cartogram of Election Results of America in 2006

由图2可以看出，按照行政区划分的最大的两个州拉贾斯坦邦（RJ）和中央邦（MP）在Cartogram上缩小，因为它们的GDP排名分别为第七和第十。GDP最高的马哈拉施特拉邦（MH）在Cartogram上略微增长，最明显的是德里（DL）的增长，虽然行政区划面积很小，但是其GDP比很多大州的都要高，而阿鲁纳恰尔邦（AR）和其他几个东北部州，虽然行政区划面积很大，但是由于GDP值落后，情况则正好相反。利用基于扩散密度均衡方法构建Cartogram需要130.6 s，而使用本文算法只要5.2 s。具体运算时间见表1。

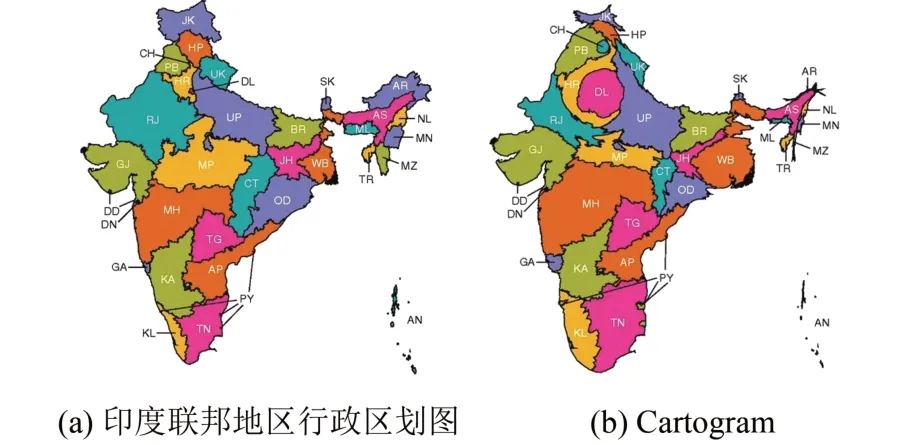
图2 2015印度联邦地区行政区划及GDP数据生成的CartogramFig.2 Administrative Divisions and Cartogram Generated by GDP Data in India

表1 基于扩散和基于热力传导的Cartogram算法的运算时间Tab.1 Calculation Time of Diffusion⁃Based Algorithm and Cartogram Based on Heat Conduction

在实验中，首先使用Albers等面积圆锥投影将地域边界的经度和纬度投影到2D空间上，将图1（a）、图2（a）嵌入一个Lx Ly的矩形框中，将其边界作为热力流动的反射边界。矩形框大小的选择需要综合考虑，在保证Cartogram与边界条件无关的条件下要尽量减少计算目标区域投影T的时间。综合考虑后，矩形框的边长等于各国南北和东西范围最大值的1.5倍。制图区域和矩形框边缘之间的空间填充有平均密度ρˉ，这样在整个矩形边框内进行变形时，边缘地区就不会对制图区域产生影响。对于离散傅里叶变换，将大矩形框划分为较小的正方形网格，使每个小正方形网格足够覆盖每张地图上的地理区域。

式（3）在数值上积分，时间步长的选择决定了估计r(1)的准确度。实现高精度制图的一种可能策略是采取大量的小步长。通过实验，本文决定采用一种不同的策略来减少运算时间：在初始积分期间，仅使用适度数量的自适应时间步长。在开始积分前，将中等宽度的高斯模糊应用于初始密度来加速收敛。算法的关键点在于使用第一次积分的输出作为下一次积分的输入，这样会更加接近客观区域。通过足够多次的积分，可以得到比较精确的结果。对于美国的48个州，进行了5次迭代后，即使是华盛顿特区的极端情况，目标区域和生成Cartogram区域的差异仅为0.31%。在印度，进行12次迭代后，安达曼和尼科巴群岛目标区域和Cartogram区域之间的最大差异为0.72%。这些细小差异是眼睛无法识别出来de，通常将最大面积误差设置为<1%。

该算法的运算速度非常快，仅用3.7 s就生成了美国选举的Cartogram，仅用5.2 s就生成了印度GDP的Cartogram。与传统扩散方法相比，该算法大大节省了时间，面积误差也较小。

4 结束语

本文算法比传统的扩散算法计算效率高，但是也存在一些问题需要改进，比如其运算不是基于shp格式的，而是通过原始数据坐标来进行的运算，虽然会加快运算速度，但是缺乏操作的简便性，后期需要在数据转换、运算方面开展进一步研究。未来还可以结合大数据来对Cartogram进行进一步创新，从多个维度进行分析，从而推动地图学的发展［10］。