基于人工神经网络的东部藏区对流层湿延迟模型

许双安 武瑞宏 刘 晨 许超钤 吕 菲

1 中铁第一勘察设计院集团有限公司，陕西西安，710043

2 轨道交通工程信息化国家重点实验室，陕西 西安，710043

3 武汉大学测绘学院，湖北 武汉，430079

4 桂林理工大学广西空间信息与测绘重点实验室，广西桂林，541004

5 川藏铁路技术创新中心有限公司，四川成都，610200

川藏铁路连续运行基准站（Sichuan⁃Tibet Rail⁃way Continuously Operating Reference Station，STR⁃CORS）综合服务系统［1］是中国首个部署于高海拔、大高差环境（青藏高原）下的网络实时动态（network real⁃time kinematic，NRTK）定位服务平台［2］，旨在为川藏铁路勘察设计、施工建造及运营维护全生命周期提供高精度的三维基准。STRCORS已在东部藏区波密至林芝段投入使用。该区域属于高原山地地貌，山高谷深，为高原温暖半湿润气候，水汽丰沛。这些特点给NRTK的作业带来了挑战。平原区的CORS系统多借助Saastamoninen（SA）经验模型［3］提供的先验对流层延迟来加快精密单点定位（precise point positioning，PPP）的收敛速度［4，5］。SA模型将对流层分为两部分进行估计：①静力学延迟分量［6］，即天顶干延迟（zenith hydrostatic delay，ZHD），该分量可由SA模型根据地表气象参数精确模拟；②湿分量［7，8］，即天顶湿延迟（zenith wet delay，ZWD），与ZHD不同的是，SA模型在高原区域无法提供高精度的ZWD估值。因此，STRCORS可利用SA模型获取ZHD，但亟需更新适用于东部藏区的湿延迟模型。

为了进一步提升STRCORS的服务质量，加快基站PPP的收敛速度，本文采用东部藏区3个探空站2017—2018年的历史观测数据，结合全球导航卫星系统（global navigation satellite system，GNSS）气象学领域应用广泛的反向传播（backpropagation，BP）神经网络［9］，建立了适用于东部藏区的湿延迟模型，将其命名为TI；并利用2019年的探空ZWD来检验TI模型的预测性能。

1 ZWD的计算方式

1.1 获取探空ZWD

探空数据是当前精度最佳的ZWD数据源［10，11］。ZWD可表示为湿折射率在地表至对流层顶的积分：

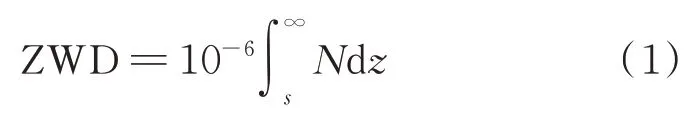
式中，s表示地表高度；N表示大气湿折射率；z表示对流层顶高度。

离散式（1）可得：

式中，Nk和Hk分别为第k层大气的湿折射率和厚度。

N计算公式如下：

式中，e表示水汽压；T表示温度；k2和k3是大气折射率常数，其取值参见Rüeger经验值［12，13］。基于探空记录，即可根据式（2）和式（3）获取探空ZWD。

1.2 利用SA模型计算ZWD

SA模型是大量CORS中控系统和高精度基线解算软件默认的对流层延迟模型［14］，该模型可根据实测或模拟地面气象参数实时估计测站处的ZWD，可表示为：

式中，Ts和es分别表示地表温度和地表水汽压；φ和h分别表示测站纬度和高程。SA模型在高原区性能不佳，无法为CORS系统提供精确的ZWD先验信息，不适合继续作为STRCORS的默认ZWD模型。因此，为了满足STRCORS的需要，本文开发了TI模型。

2 TI模型的建立

STRCORS部署在西藏自治区东部，此区域目前存在3座探空站，分别是拉萨站（代号55591）、那曲站（代号55299）和昌都站（代号56137）。上述探空站历史数据保存完备，可为TI模型的建立提供高质量的ZWD源数据。因此，本文收集了以上3座探空站2017—2018年的探空记录，用于TI湿延迟模型建模。

2.1 数据预处理

本文将得到的探空ZWD作为唯一的输出参数参与TI模型的建立。根据式（4），ZWD与Ts和es高度相关。Ts、es又与气压P存在显著的相关关系。因此，将上述3个气象变量作为输入。另外，采用两个时间变量，即年和年积日（day of year，DOY）来表征ZWD的时间变异性。故年和DOY联合3个气象参数共同组成输入参数。输入和输出参数确定后，本文制备了相应的建模（输入和输出）数据集，用以生成TI模型。

2.2 确定BP神经网络的结构

BP神经网络是强大高效的建模工具［15，16］，可拟合复杂非线性关系。本文采用BP神经网络来构建TI模型。采用的人工神经网络由5节点的输入层、4节点的隐藏层和单节点的输出层构成。双曲正切函数为隐藏层各节点间的激活函数，线性函数为输出层的激活函数［9，15］。确定神经网络的结构后，输入5参数输入数据集和单参数输出数据集，基于Leven⁃berg⁃Marquardt算 法［9］训练，即可训练并生成TI模型。

3 模型测试

本文以那曲站、昌都站、拉萨站为例，对比了2019年的探空ZWD（真值）、SA模型获取的ZWD（SA⁃ZWD）与TI模型获取的ZWD（TI⁃ZWD），结果见图1。SA模型虽然可在一定程度上反映ZWD随DOY的变化趋势，但存在明显的估计不足问题；TI⁃ZWD与探空ZWD贴合较优。图2展示了利用SA模型和TI模型获取的ZWD在3个探空站处的偏差随DOY的分布情况。可以看出，SA模型的性能在夏秋季节（DOY150~290）最差，偏差高达20 cm，而TI模型的性能稳定，全年维持在0 cm上下。

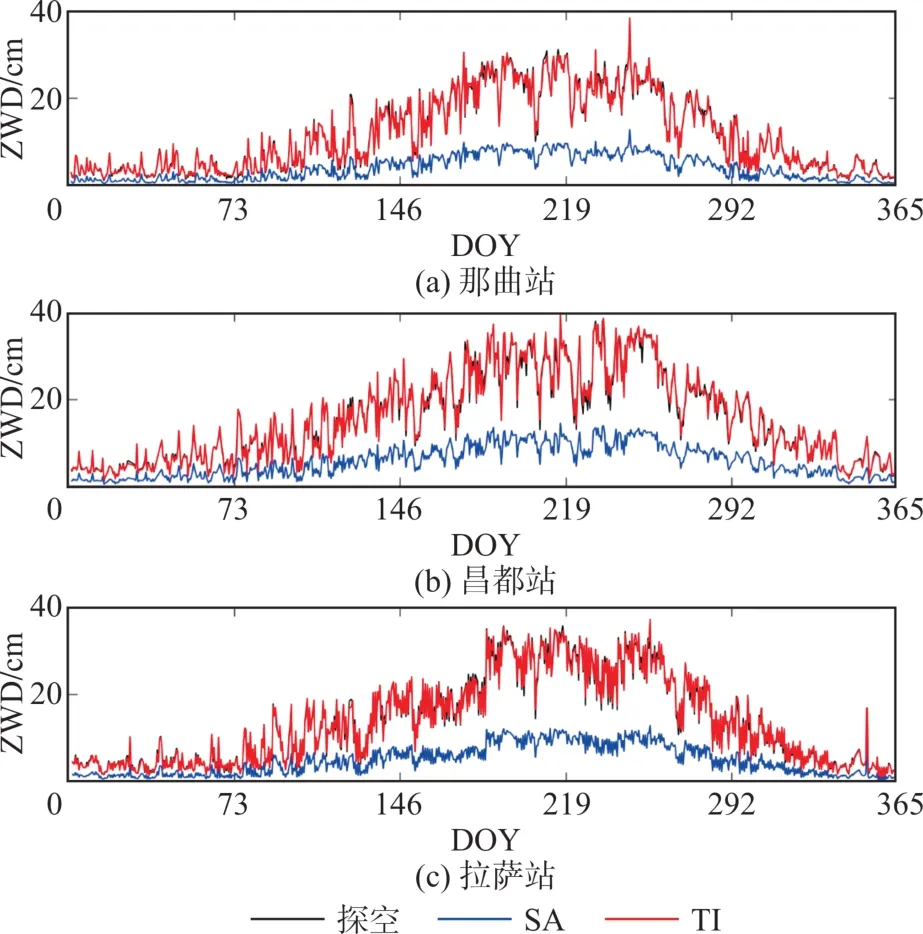
图1 3座探空站处的探空ZWD、SA‐ZWD、TI‐ZWDFig.1 Radiosonde ZWD，SA⁃ZWD and TI⁃ZWD at Three Radiosonde Stations

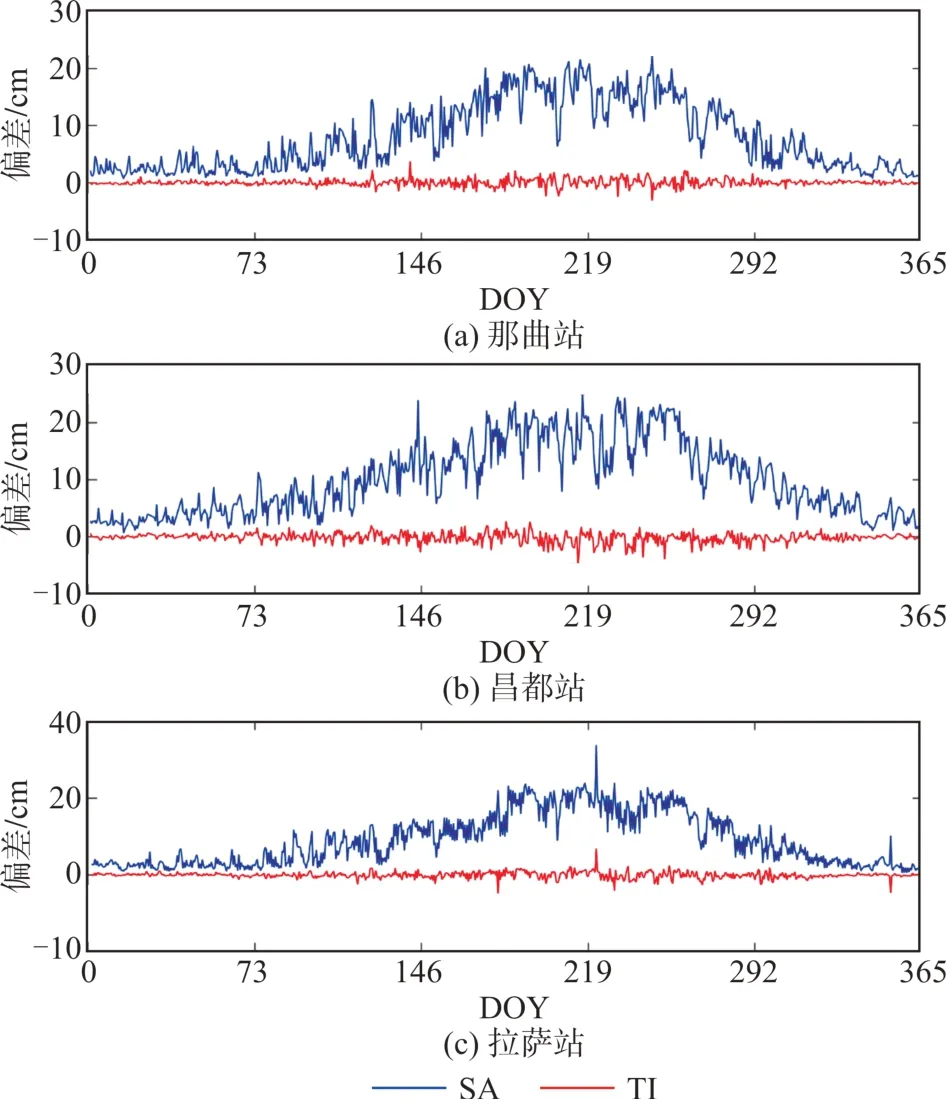
图2 SA‐ZWD、TI‐ZWD在3座探空站处的偏差随DOY的分布情况Fig.2 Distribution of Bias of SA⁃ZWD and TI⁃ZWD at Three Radiosonde Stations with DOY

图3和图4分别展示了SA模型和TI模型在3座探空站处的精度表现。可以看出，SA⁃ZWD、TI⁃ZWD均与探空ZWD高度相关，相关系数均为0.99。但是，TI模型的偏差和均方根误差（root mean square error，RMSE）在3个探空站处均明显优于SA模型。另外，表1列出了SA模型和TI模型在实验中的平均偏差和RMSE。SA模型的平均偏差和RMSE分别为9.1 cm和11.1 cm；TI模型的平均偏差和RMSE分别为0.0 cm和0.8 cm。综上，在东部藏区，利用SA模型估计湿延迟存在估计不足的缺陷，而TI模型的ZWD估值具有无偏性，且各项指标都证明TI模型的性能显著优于SA模型。

表1 SA模型和TI模型的平均偏差和RMSE/cm Tab.1 Bias and RMSE Values of SA and TI Models/cm

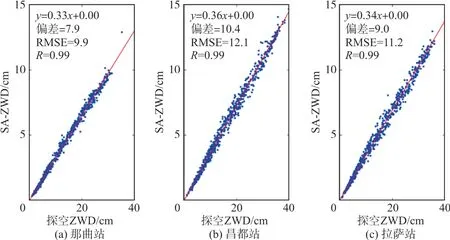
图3 SA‐ZWD与探空ZWD在3座探空站处的拟合情况Fig.3 Fitting of SA⁃ZWD and Radiosonde ZWD at Three Radiosonde Stations

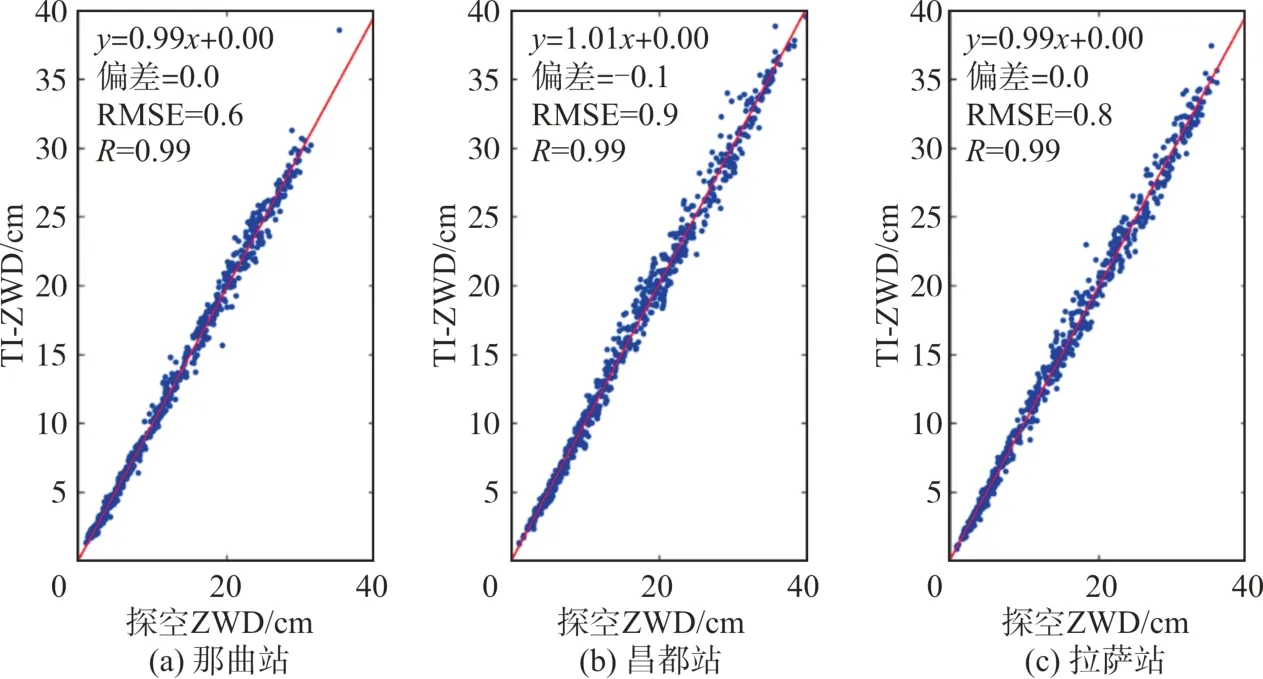
图4 TI‐ZWD与探空ZWD在3座探空站处的拟合情况Fig.4 Fitting of TI⁃ZWD and Radiosonde ZWD at Three Radiosonde Stations

4 结束语

为了满足STRCORS对高精度ZWD先验信息的需要，本文基于BP神经网络，采用那曲站、昌都站和拉萨站2017—2018年的探空数据建立了适用于东部藏区的ZWD模型——TI模型。并采用上述3个探空站2019年的探空ZWD测试了TI模型的预测性能。测试结果表明，在STRCORS所在的东部藏区，TI模型的预测精度显著优于广泛使用的SA模型。未来TI模型将上线STRCORS，提升波密至林芝段的NRTK服务质量。