拓扑材料BaMnSb2 的红外光谱学研究

邱子阳 陈岩 邱祥冈

1) (南京电子器件研究所,南京 210016)

2) (中国科学院物理研究所,北京凝聚态物理国家研究中心,北京 100190)

3) (中国科学院大学物理学院,北京 100049)

4) (量子物质科学协同创新中心,北京 100084)

对于新型拓扑材料BaMnSb2,研究了从7 K 到常温下温度依赖的宽频红外光谱特性.随着温度的降低,绝对反射谱中等离子体极小值有着明显的蓝移,表明载流子浓度存在随温度变化的行为.在光电导谱的实部中存在两段随着频率线性增加的响应,它们的线性外延不经过原点,表明BaMnSb2 的费米能级附近有打开能隙的Dirac 型色散.此外,在低温下还发现了一段不随频率变化的光电导,且无法用传统的Drude-Lorentz模型拟合.因此本文引入了一个恒定的光电导分量,得到了满意的拟合结果.通过计算和分析,我们认为恒定光电导分量可能来自于拓扑材料BaMnSb2 的表面态响应.

1 摘 要

近几年,拓扑材料因其丰富的物理性质,在量子材料和凝聚态物理领域引起了广泛的关注.根据动量空间中的能带是否存在能隙以及简并的情况,可将拓扑材料大致分为拓扑绝缘体[1,2]、Dirac 半金属[3-6]和Weyl 半金属[7,8].对于拓扑绝缘体,体态在费米能级附近存在能隙,表现为绝缘态,而表面态在费米能级上是能带交叉的,表现出金属态.对于Dirac 半金属,费米能级附近的导带和价带具有线性色散并且交叉形成Dirac 点,在三维动量空间中形成Dirac 锥状的分布.当Dirac 半金属的时间反演或者空间反演被破坏时,Dirac 点会劈裂成一对具有相反手性的Weyl 点,材料演变成Weyl 半金属.由于拓扑材料有着丰富的量子特性[9-11],研究这类材料有助于进一步理解拓扑相变以及拓扑相理论.

研究发现,在三维动量空间的电子态分布中,Bi 和Sb 与Mn 的化合物在费米能级附近容易形成各向异性的线性色散.由于Mn 元素具有反铁磁序,科学家们对新型磁性拓扑材料AMnBi2和AMnSb2(A=Ca,Sr,Ba,Eu 和Yb)进行了大量研究[12-26],希望能在其中发现新奇的拓扑特性.文献[27]通过理论计算预言在AMnSb2系列中,只有当晶体空间群为I4/mmm时,材料才会表现出Dirac 费米子行为.对于满足I4/mmm晶体群的BaMnSb2材料,戎洪涛等[28]报道了通过ARPES观测到了宽能量范围的连续Dirac 费米子行为,但理论计算Dirac 点在费米能级附近有能隙打开,与实验观测不同.为了解决这一矛盾,我们对拓扑材料BaMnSb2进行了细致的红外光谱研究.由于BaMnSb2与YbMnSb2结构相同,利用红外光谱技术也将帮助我们判断在BaMnSb2中是否也存在Dirac nodal-line 的行为.

不同的拓扑特性在红外光谱学中有不同的光学响应.对于拓扑材料,由于费米能级附近的特殊电子态分布,会使得光电导的实部σ1(ω)在低频波段随着频率ω出现特殊的线性分布:

其中d表示拓扑系统的维度[29-31].对于二维拓扑材料(d=2),光电导的实部σ1会表现出不随频率ω变化的特性;对于三维拓扑材料(d=3),σ1(ω)会随着ω线性增加,且低频线性外延经过原点.而对于具有nodal-line 结构的Dirac 半金属,如ZrSi S[32-34],NbAs2[35]和YbMnSb2[25],由于具有特殊的Dirac 点分布,已经在红外光谱研究中发现了具有不随ω变化的恒定光电导分量.因此,利用红外光谱学可以非常有效地帮助我们判断BaMnSb1的拓扑特性:当线性外延通过原点时,证明存在连续的Dirac 费米子;当线性外延不经过原点,证明Dirac 型色散有打开的能隙.

本文通过对BaMnSb2进行详细的红外光谱学研究,发现在光电导的实部σ1(ω)中有两段随频率线性增加的σ1(ω),其线性外延均不经过原点,证明费米能级附近有打开能隙的Dirac 型色散.与文献[28]对比,发现两段线性光电导的起始频率与能带图中电子态的能隙大小一致,进一步证明了第一性理论计算的正确.此外,在低频波段发现了一段恒定的σ1(ω)分量,通过计算和分析,猜想这段恒定组分可能来自BaMnSb2的表面态.

2 实 验

利用自助熔的方法成功烧制出了高质量的层状单晶材料BaMnSb2[28].借助原位镀金的技术[36]和Bruker Vertex 80v 傅里叶红外光谱仪,测得了BaMnSb2在ab面上不同温度 下(7—295 K 共14 个温度点)连续的反射谱R(ω),频率从50 cm—1到15000 cm—1.对于可见光和紫外波段(15000—30000 cm—1),利用Avaspec 2048×14 光纤光谱仪测量室温下的绝对反射谱.通过Kramers—Kronig(KK)变换,由R(ω)可以计算出描述联合态密度的实部光电导谱σ1(ω).在计算过程中,对于ω <50 cm—1使用Hagen—Rubens 模型进行外推;30000 cm—1<ω<12.4 eV 部分假设为恒定分量;ω＞ 12.4 eV部分则认为是自由电子响应(ω−4).

3 结果

3.1 反射谱

图1 给出了BaMnSb2在5 个不同温度下频率0—3000 cm—1的绝对反射率R(ω).在ω=100200,和400 cm—1附近可以发现3 个非常明显的红外活性声子[37].当频率接近零频,R(ω)迅速升高并接近1;在ω=700 cm—1附近存在非常陡峭的等离子边,体现了材料的半金属特性.随着温度降低,等离子体边逐渐向高频移动.此外,在该波段R(ω)的最低点—等离子极小值随着温度的降低有明显的蓝移行为.对于ω大于3000 cm—1的高频波段,R(ω)几乎完全重合,且从图1 的插图中可以观察到多个明显的鼓包,表明BaMnSb2在高频存在带间跃迁.

图1 BaMnSb2 在5 个 温度点50—3000 cm—1 范围内 的反射率.插图为室温下到30000 cm—1 的反射谱Fig.1.Reflectivity of BaMnSb2 at five representative temperatures between 50—3000 cm—1.The inset displays the reflectivity up to 30000 cm—1 at room temperature.

3.2 光电导谱

基于KK 变换,可以算出图1 反射谱对应的光电导谱的实部σ1(ω),如图2 所示.可以看出,在低频σ1(ω)有非常明显 的Drude 峰,随着温度升高Drude 峰逐渐变宽.图2 中的插图展现了直到ω=30000 cm—1的σ1(ω),可以发现Drude 分量在整个光电导谱中占比很小,说明BaMnSb2的载流子浓度低,与R(ω)中观察到的半金属特性一致.

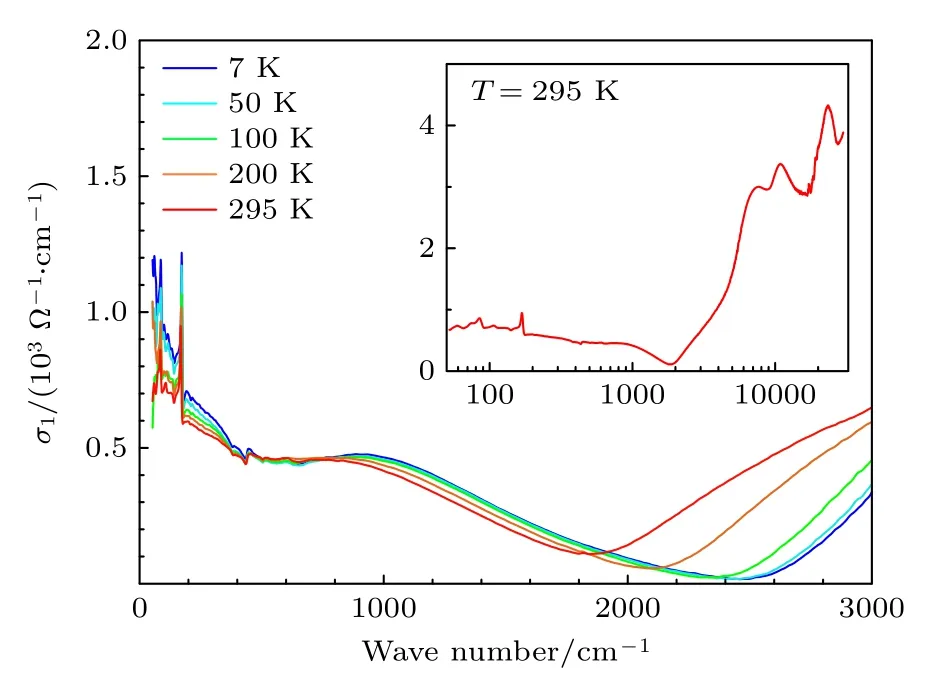
图2 通过Kramers-Kronig 计算得到相应的光电导的实部.插图为室温下到更高频率的光电导谱Fig.2.The corresponding real part of optical conductivity σ1(ω) is calculated through Kramers-Kronig transformation.The inset shows σ1(ω) over a broad frequency range at room temperature.

对于ω >2400 cm−1的高频波段,有两段非常明显的随频率线性增加的σ1(ω),分别是2650—3500 cm—1和3500—5000 cm—1,如图3 的虚线所示,说明电子态在费米能级附近存在Dirac 型的色散.对这两段线性光电导进行线性低频外延,发现均不过原点,证明BaMnSb2的Dirac 型色散存在能隙,与理论计算的结果相符[28].两段线性部分的起始频率2650 cm—1和3500 cm—1,分别对应0.33 eV 和0.434 eV 的带间跃迁.

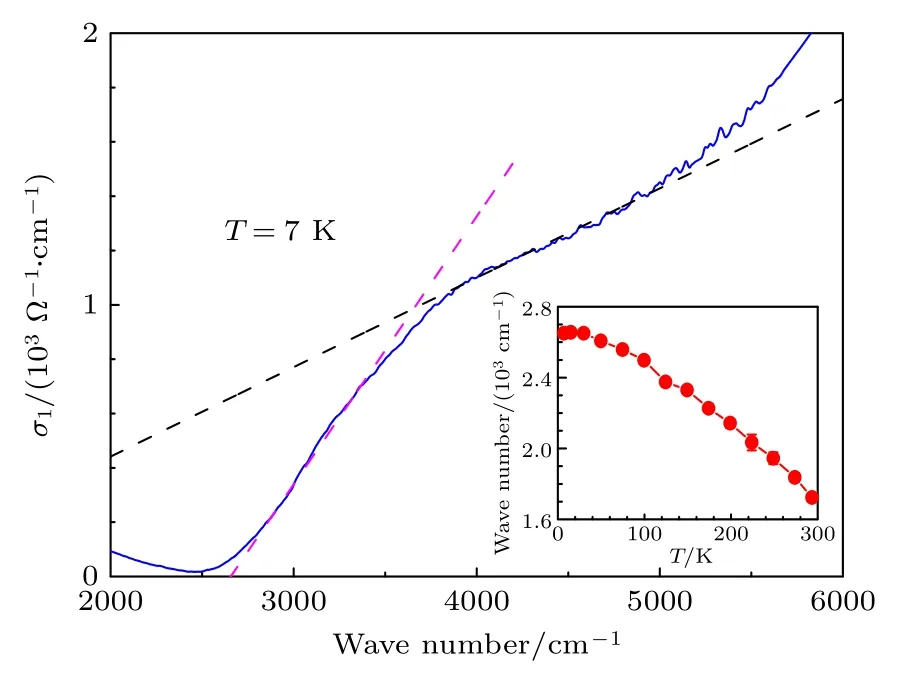
图3 蓝色实线为7 K 时BaMnSb2 在高频波段的光电导谱,粉色虚线和黑色虚线分别示意了两段线性增加的光电导.插图是不同温度下粉色虚线线性外延与横坐标的交点,对应了Dirac 能隙随温度变化的关系Fig.3.The blue solid curve is σ1(ω) for BaMnSb2 at 7 K in high-frequency range.The pink and dark dashed lines denote two range of linearly-increased σ1(ω).The inset exhibits extrapolation of the pink dashed line to zero conductivity at finite frequency,corresponding to the temperaturedependent Dirac gap.

在文献[28] 的理论计算中,M-Y的方向上存在一个打开能隙的Dirac 型电子态分布,能隙大小约为0.38 eV;而在Γ点处带隙的大小约为0.48 eV,由于Γ点附近导带和价带的分布是准线性的,其带间跃迁在σ1(ω)中同样会贡献一段线性分量.因此,在合理的误差范围内,σ1(ω) 中观测到的两段线性光电导与理论计算相符,即2650—3500 cm—1的线性光电导响应对应了M-Y的Dirac型带间跃迁,而3500—5000 cm—1的线性响应对应了Γ点附近的带间跃迁.通过线性外延粉色虚线与横坐标的交点,可以得到Dirac 能隙随温度变化的依赖关系,如图3 中的插图所示.

为进一步分析σ1(ω)的低频部分(0—2000 cm—1),引入经典的Drude-Lorentz 模型:

须知道,在利用Drude-Lorentz 模型分析σ1(ω)时应尽量少地引入模型个数.在拟合的过程中我们分别尝试了(i) 1 个Drude+2 个Lorentz分量;(ii) 2 个Drude+1 个Lorentz 分量,但都无法很好地拟合出低温时400—1200 cm—1的光电导谱.有趣的是,我们意识到在低频波段存在一段恒定的σ1(ω) ,其值大约为450Ω−1·cm−1,如图4 的虚线所示.计算7 K 温度时光电导的谱重S(ω)=,如图4 中的插图所示,很明显,在频率为350—1150 cm—1的范围内,σ1(ω)随着ω线性增加,这进一步证明了σ1(ω)在低频存在一段恒定的光电导,与YbMnSb2的红外光谱结果非常相似[25].

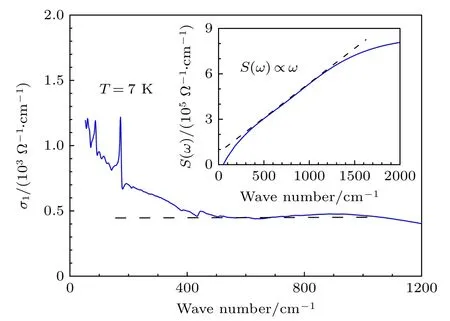
图4 BaMnSb2 在7 K 时的 σ1(ω) ,其中黑色虚线注明 了恒定光电导组分.插图为 σ1(ω) 的谱重随频率变化的关系,其中黑色虚线表明在350—1150 cm—1 范围内谱重随频率线性增加Fig.4.σ1(ω) for BaMnSb2 at 7 K.The dark dashed line denotes the frequency-independent component.The inset portrays the spectral weight S (ω) at 7 K,and the dark dashed line represents S (ω) follows an ω behavior in the range between 350—1150 cm—1.

根据以上的讨论,我们尝试在Drude-Lorentz模型中引入一个恒定光电导分量,并成功拟合出了所有温度下的σ1(ω).图5 给出了3 个温度下的拟合曲线,如蓝色虚线所示,证明了不同温度下σ1(ω)在300—1200 cm—1范围内,都有一段值为147 Ω−1·cm−1的恒定光电导分量.这种不寻常的光电导响应通常出现在二维狄拉克系统中,如石墨烯[38-40],但BaMnSb2是三维层状材料.因此合理猜想BaMnSb2在费米能级附近可能存在nodalline 的Dirac 分布,就像ZrSiS[32,41]和YbMnSb2[25].

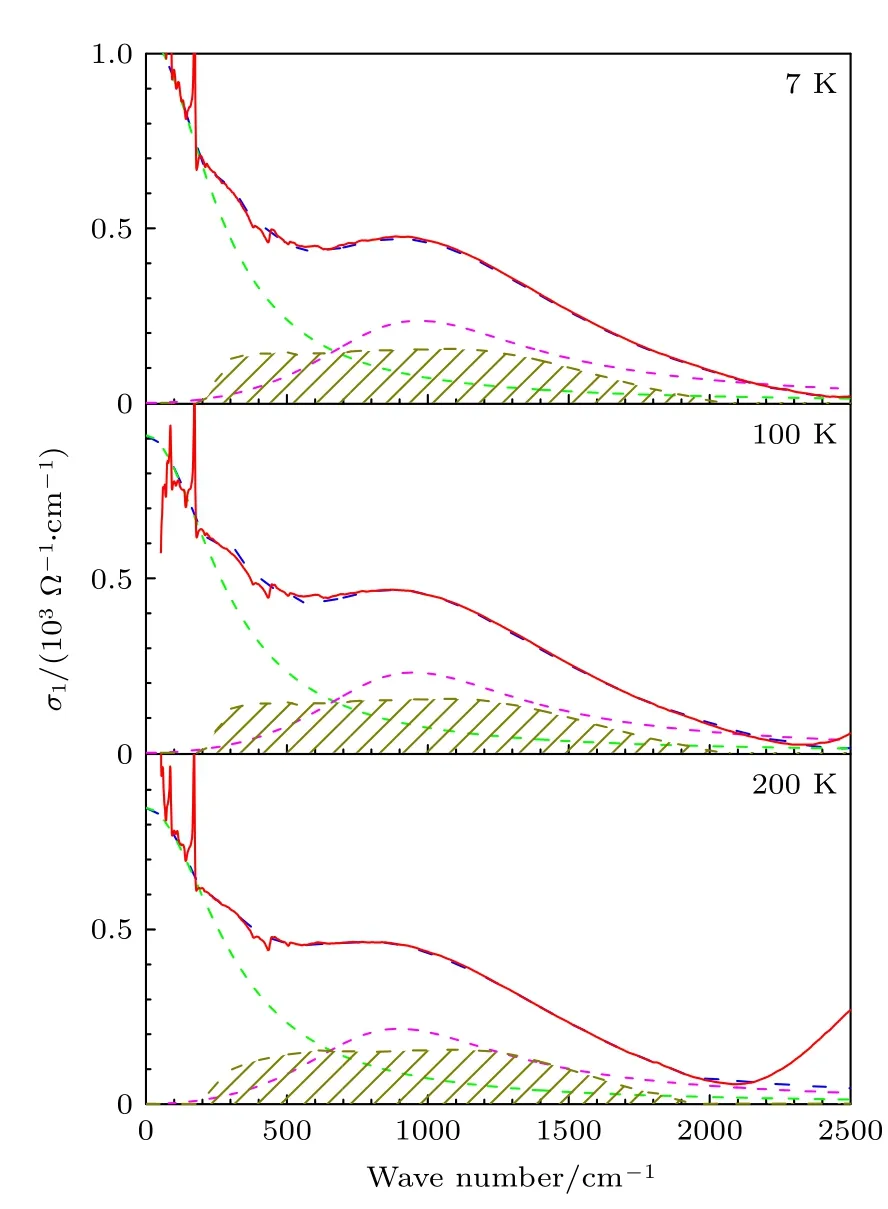
图5 σ1(ω) 在0—2500 cm—1 范围内的拟合结果,拟合的组分为一个绿色的Drude 分量,一个粉色的Lorentz 分量,和一个深黄色的恒定分量.对于100 和200 cm—1 附近的红外活性声子暂不讨论Fig.5.Fitting results for σ1(ω) in 0—2500 cm—1 frequency range,which is decomposed into one Drude term (green dashed line),one Lorentz term (pink dashed line),and a constant component (dark yellow dashed line).The infrared-active phonons near 100 and 200 cm—1 are ignored.

3.3 讨论

文献[28]通过角分辨光电子能谱和理论计算,细致讨论了三维Dirac 材料BaMnSb2.在根据第一性原理计算的能带结构中,只观察到在M-Y的方向上存在一个Dirac 型电子态分布.此外,恒定的光电导分量起始频率为300 cm—1,在能带结构中没有对应的带间跃迁.因此从能带结构中,没有发现BaMnSb2材料在费米能级附近存在nodalline 型的Dirac 分布.

关于产生恒定光电导分量的原因,排除了nodal-line 型Dirac 分布的可能性,另一个猜想是由BaMnSb2材料的表面态引入的.在YbMnSb2中恒定光电导的σ1(ω)≈340 Ω−1·cm−1[25],而BaMn Sb2中只有147Ω−1·cm−1,低于YbMnSb2中的值.分别计算两种材料的恒定光电导谱重S(ωconstant)与相应频率σ1(ω)的谱重S(ω)的比值,发现YbMn Sb2的恒定光电导分量占比为0.58,而BaMnSb2的占比只有0.3.由于BaMnSb2的恒定光电导分量非常小,且在体能带中没有对应的带间跃迁,所以我们猜想该分量代表的电子激发可能来自于表面态.我们知道三维Dirac 材料的表面态是拓扑非平庸态,在费米能级上具有二维Dirac 的电子态分布,表现在σ1(ω)中为一段随频率恒定不变的光电导.因此我们认为BaMnSb2的恒定光电导分量来自于表面态的二维Dirac 分布.

4 结论

本文从7 K 到室温对拓扑材料BaMnSb2进行了细致的红外光谱学研究.我们发现在反射谱中ω=700 cm−1附近有非常陡的等离子边,且其随着温度降低逐渐向高频转移.等离子体边极小值随着温度降低也明显蓝移.基于KK 关系,计算得到了对应的光电导谱的实部σ1(ω) ,发现在 2650—3500 cm−1和 3 500—5000 cm−1存在两段随频率线性增加的σ1(ω),证明电子态在费米能级附近存在Dirac 型色散;由于其线性外延均不经过原点,说明Dirac 型色散存在能隙;通过与理论计算对比,我们发现两段线性光电导的起始频率与能带结构中的能隙大小一致,进一步证明了第一性理论计算的正确.最后,在低频波段还发现了一段恒定的光电导分量,通过计算和分析,我们认为这段恒定光电导来自BaMnSb2的表面态.