径向磁场对霍尔推力器性能影响的数值模拟研究*

杨三祥 王倩楠 高俊 贾艳辉 耿海 郭宁 陈新伟 袁兴龙 张鹏

(兰州空间技术物理研究所 真空技术与物理重点实验室,兰州 730000)

霍尔推力器由于推力密度大、结构简单等特点,在商业航天领域具有广泛的应用前景.为了进一步提升小功率霍尔推力器的性能,克服低轨卫星用小功率霍尔推力器性能受限于输入功率和最大磁场强度的问题,本文利用数值模拟和理论分析方法研究了霍尔推力器放电通道中径向磁场分布对推力器性能的影响.在轴向磁场分布和最大径向磁场强度一定的情况下,通过改变径向磁场梯度实现径向磁场对推力器性能影响的研究.结果表明,在放电参数、推进剂流率以及轴向磁场不变的情况下,加速区的电势随着径向距离的增加而减小.因此,靠近推力器放电通道内壁侧的径向磁场梯度越大,离子沿着轴向漂移到达推力器出口的动能越大,推力器的推力越大.本文的研究结果为霍尔推力器的磁场设计,性能优化提供了理论支撑.

1 引言

霍尔推力器作为一种静电型电推力器,相较于离子推力器[1,2]具有推力密度大、推功比高、结构简单等特点[3].目前,霍尔推力器已广泛用于执行卫星的位置保持和轨道修正等任务,特别是在商业航天领域,如低轨互联网星座[3].

关于霍尔推力器的研究目前主要集中在以下几个方面:1)降低推力器壁面溅射腐蚀,提高推力器工作寿命[4].为了减少离子对壁面的溅射腐蚀,通常采用优化磁场拓扑结构的方法,使磁力线尽可能平行于放电通道壁面并深入通道底部,形成具有磁屏蔽效应的磁场位形[5].具有磁屏蔽效果的磁场位形一方面可以减少离子对壁面的轰击,另一方面可以有效减小阳极的热负载[6],从而有效延长推力器的工作寿命.2)提升推力器的性能[7,8].霍尔推力器性能的提升主要是通过优化物理设计来实现,特别是优化放电通道内的磁场位形[9,10,11].在满足电子磁化、离子非磁化这一基本要求的前提下,一方面使最大磁场强度所对应的轴向位置尽可能向推力器出口下游移动,另一方面使放电通道内的磁场具有较大的轴向磁场梯度[12].3)实现推力和比冲的独立调节[13].随着航天任务的复杂性增加,同一颗卫星在不同任务阶段会对推力器的工作模式提出不同的要求:在卫星轨道提升和轨道转移期间,需要大推力模式以缩短卫星变轨所需时间;在卫星位置保持期间,则要求高比冲模式以减少推进剂的消耗,增加推力器在轨工作时间[14].传统的霍尔推力器由于特殊的磁场位形使得位于放电通道内的电离区和加速区相互重叠[15],很难实现推力和比冲的独立调节.Perez 等人研究表明具有双峰磁场的附加电极霍尔推力器在一定程度上可以使推力器的电离和加速过程分离,从而有望实现推力和比冲的独立调节[14].4)削弱或抑制放电振荡,提高放电稳定性[16].霍尔推力器在工作过程中由于粒子间的碰撞、物理量梯度的存在,以及等离子体的固有振荡,导致推力器在放电过程中会出现频率介于kHz～GHz 范围的放电振荡[17].如由电离碰撞引起的频率介于10—30 kHz 的“呼吸”振荡[18,19];由羽流区的密度梯度和磁场梯度诱发的沿着E×B或者−E×B方向传播的“旋转辐条”不稳定性[20,21].霍尔推力器中的低频、大幅放电振荡一方面会使羽流发散角增加,加剧壁面的溅射腐蚀,缩短推力器的工作寿命,另一方面严重的放电振荡会导致推力器熄弧[22].

综上可知,霍尔推力器工作寿命、性能、工作模式、放电振荡等都与磁场特性有关[10].Mikellides等[5]利用二维轴对称模型研究了霍尔推力器在寿命初期和寿命末期平行于壁面的电场和鞘层电势降的变化,揭示了磁屏蔽设计延长霍尔推力器寿命的机理.Hofer 等[9]利用试验数据,采用唯象模型揭示了磁场对高比冲霍尔推力器的重要影响.Hara等[23]利用微扰分析方法研究了电子输运、电子温度及中性原子通量对“呼吸”振荡的影响,结果表明电子能量在壁面上的损耗对电离不稳定性有稳定作用.Brown 等[24]研究了等离子体与壁面相互作用导致的霍尔推力器的溅射腐蚀,结果表明壁材料的溅射腐蚀与材料的特性、磁场、放电电压等因素有关.康小录等[25]开展了磁场对高电压霍尔推力器影响的研究,结果表明在不固定磁场构型时,增加磁场强度推力器效率存在两个极大值;固定磁场构型时,增加磁场强度推力器效率只有一个最大值.丁永杰等[26]开展了磁场对霍尔推力器壁面侵蚀的研究,结果表明聚焦磁场相对于发散磁场能够有效降低离子对壁面的侵蚀,进而提高推力器工作寿命.于达仁等[27]研究了磁场位形对双级霍尔推力器中离子输运的影响,结果表明磁场位形通过影响电势分布实现对离子输运过程的调控.段萍等[28]研究了磁零点位置对霍尔推力器放电特性的影响,结果表明磁零点的位置影响推力器放电,以及离子对壁面的溅射腐蚀.需要说明的是,上述研究只关注了霍尔推力器轴向磁场分布或磁场强度大小对推力器性能、寿命等的作用,忽略了磁场径向分布的影响.事实上,应用于低轨卫星的小功率霍尔推力器,由于功率、最大磁场强度等受限,通过提升磁场强度和增加输入功率实现推力器性能提升的方法将不再适用,因此需要研究推力器性能提升的其他有效方法.

本文依托兰州空间技术物理研究所研制的LHT-70 霍尔推力器,采用二维混合模型和理论分析开展了径向磁场分布对霍尔推力器性能影响的研究.本文旨在通过研究不同径向磁场分布对推力器性能的影响,明确径向磁场与推力器性能的依赖关系,为霍尔推力器产品性能优化、磁场设计提供理论支撑.

2 模型方程

霍尔推力器中由于磁场对电子的约束作用,导致在磁场强度最大位置处(推力器出口附近)会形成一个局部的高密度电子区.电子的局部集中一方面会增加电子与中性原子的碰撞概率,使大量的原子在该区域被电离.另一方,电子的局部集中在放电通道内形成虚阴极,使空间电势在该位置处发生陡降,形成一个大的轴向电场,用于带电粒子的轴向加速.霍尔推力器放电通道中电势分布满足泊松方程

在式(3)中引入虚拟时间τn,上述方程变为如下形式[28]

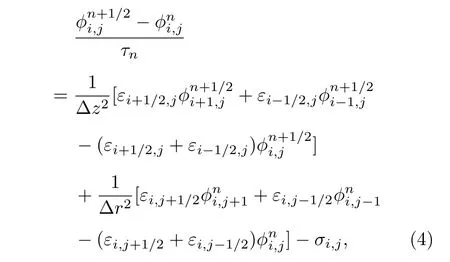
式中,Δz和 Δr分别代表z方向和r方向的空间步长,且满足 Δz=Δr.当τn →∞时,∂φ/∂τn=0,则φ为方程的解,由φ可以求出空间电场.

带电粒子运动满足方程

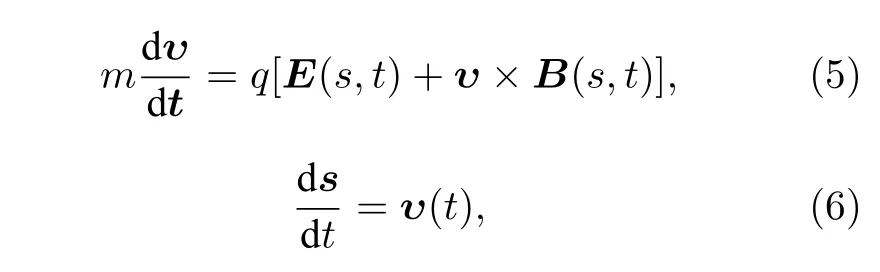
式中,s和υ分别表示位置和速度矢量,E和B表示电场强度和磁场强度,m和q分别表示带电粒子的质量和电荷.初始时刻从推力器气体分配环进入放电通道的中性原子位置由蒙特卡罗抽样方法确定.粒子位置在轴向和径向上的分布满足

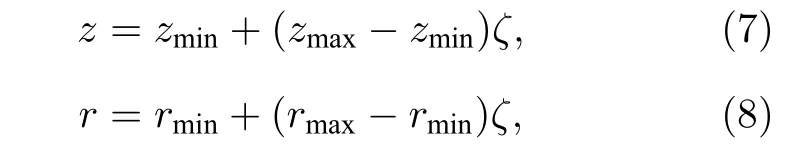
式中:zmax,zmin和rmax,rmin分别为计算区域在轴向和径向位置的最大和最小值;ζ表示介于0 和1 之间的随机数.假设中性原子以热速度从推力器阳极进入且速度满足Maxwell 分布,位置和速度按照定义的循环步长进行更新.当电子与原子发生弹性碰撞时,电子的动能εe保持不变;当电子与原子发生激发碰撞时,电子会有8.32 eV 的能量损失;当电子能量超过工质原子的第一电离能时,电子与原子发生电离碰撞形成离子,未被电离的中性原子的运动轨迹保持不变.

由于霍尔推力器中复杂的物理过程主要发生在放电通道中,因此在二维模拟研究中计算区域只包含霍尔推力器放电通道内部,如图1 所示.由于阳极和推力器出口处电势固定,所以采用第一类边界条件进行处理.推力器通道内、外壁面为绝缘壁面,电子撞击到壁面上会产生包括电子在壁面上沉积,二次电子发射、非弹性反射及弹性反射等物理过程,导致绝缘壁面上的电势会出现浮动.因此,绝缘壁面采用第二类边界条件,通过表面电荷密度σ可以求得垂直于壁面的电场.下标“wi”和“wo”分别表示内壁面和外壁面.为了避免求解泊松方程过程中引起的数值不稳定性,网格采用正方形均匀网格.采用Boris 蛙跳算法,通过求解粒子在电磁场中的运动方程对带电粒子位置和速度进行更新[26].为了保证计算结果的可靠性,时间步长 Δt需要同时满足ωpΔt<0.3 和ωcΔt<0.2的限制条件.其中为电子振荡频率,ωc=qB/me为电子回旋频率.在本文给定的计算条件下 Δt ≈3×10−12s.

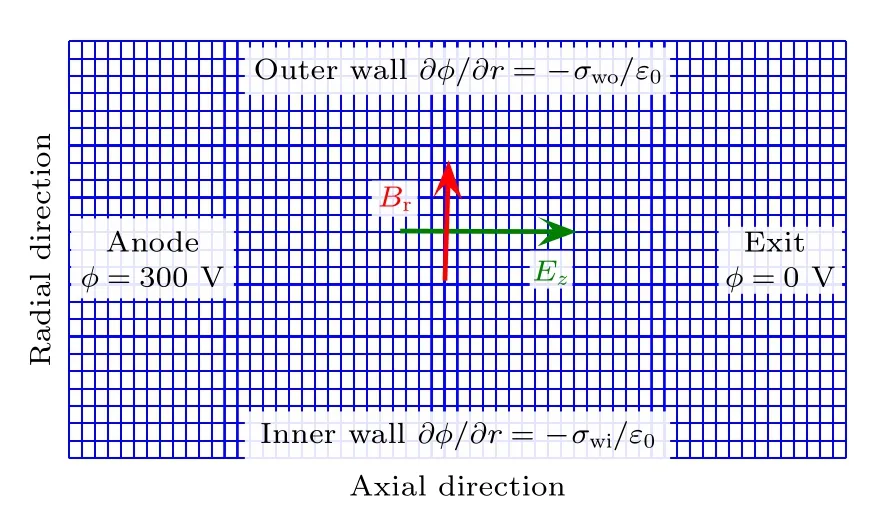
图1 计算区域和边界条件.Fig.1.Simulation region and boundary conditions.

3 数值计算结果

为了简单,通常在霍尔推力器的二维模拟中假设磁场沿着径向是均匀分布的.事实上,由励磁线圈产生的磁场其径向磁场强度Br满足Br∝1/r,r为距励磁线圈中心的径向距离.因此,霍尔推力器中由内、外励磁线圈嵌套产生的磁场在径向上并非均匀分布而是随径向距离r的增加先减小后增加,即磁场强度随径向距离的增加呈现“U”型.为了研究真实磁场位形对推力器性能的影响,本文比较了2种不同径向分布的磁场位形:B1(z,r)=B(z)·B1(r),B2(z,r)=B(z)·B2(r).B(z)表示磁场沿着轴向的分布,B(r)表示磁场沿着径向的分布,下标“1”、“2”分别表示2 种不同的径向磁场分布.其中B1(r)=B0,m ax(B2(r))=B0,B0为推力器放电通道出口处最大磁场强度.为了描述方便,定义Bei为推力器出口内壁侧的磁场强度,Beo为推力器出口外壁侧的磁场强度.对于磁场分布为B2(z,r)的情形,在计算中通过固定Bei=B0,改变径向最小磁场强度的大小及其位置实现不同径向磁场分布对推力器性能影响的研究.

3.1 径向磁场强度分布满足 B1(r)=B0

当推力器出口处径向磁场强度为常数B0=220 Gs时,位于推力器放电通道内的磁场强度分布如图2 所示.轴向和径向位置分别用推力器放电通道的长度和放电通道外半径进行归一化处理,磁场强度用B0进行归一化处理.需要说明的是,霍尔推力器中不存在径向磁场强度为常数的磁场分布,这里为了比较磁场的径向分布对推力器性能的影响,人为设计了径向磁场强度为常数的算例.LHT-70 霍尔推力器在放电电压Ud=300 V,阳极工质流率m˙=2.7 mg/s ,阴极工质流率为 0.1 mg/s,内外励磁线圈励磁电流分别为2.1 A 和2.5 A 时,试验测得的推力T=41 mN ,比冲Isp=1550 s.为了便于比较,在模拟中采用与试验相同的电气参数.

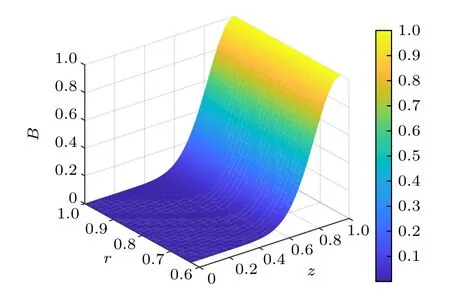
图2 放电通道内磁场分布Fig.2.Magnetic field distribution in discharge channel.

当推力器出口处的径向磁场强度为B0时,计算得到的推力和比冲如图3 所示.推力平均值=30.13 mN ,比冲的平均值为=1656 s.数值计算的推力小于试验值,一方面是计算区域只包含了推力器放电通道内部,忽略了推力器出口下游的羽流区.在霍尔推力器中由于加速区位于推力器出口附近,部分离子在离开放电通道后被位于推力器出口下游的羽流区电场进一步加速,离子速度进一步增加.另一个可能原因是径向磁场强度为常数.径向上相同大小的磁场强度使磁场对电子的约束能力完全相同,从空心阴极发射的电子被约束在推力器出口附近,由于能量太低而不能与中性原子发生有效电离碰撞,从而导致工质利用率低,离子数密度小,最终使得计算值小于试验值.模拟得到的比冲大于试验值是因为模拟中比冲由离开推力器出口处的离子速度计算得到,即Isp=vext/g.

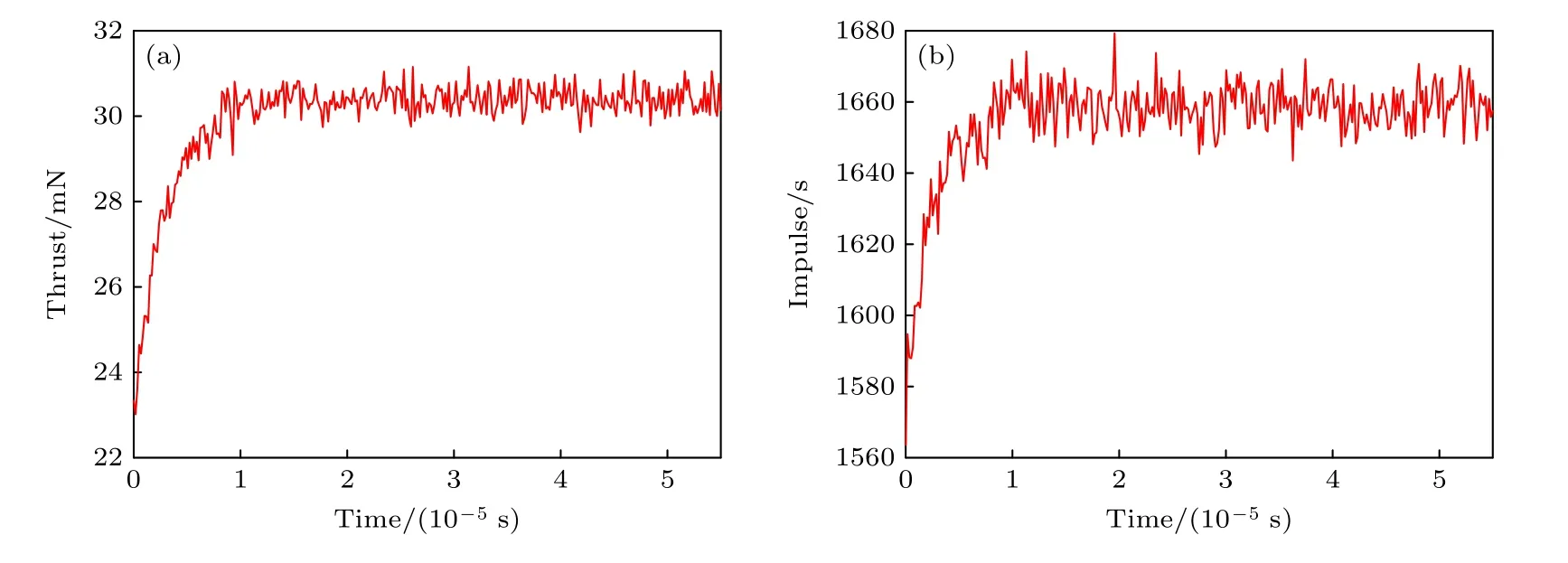
图3 (a)推力和(b)比冲Fig.3.The (a) thrust and (b) specific impulse.

3.2 径向磁场强度分布满足 max(B2(r))=B0

图4(a)为当 max(B2(r))=B0=Bei=220 Gs时放电通道内磁场的分布.由于磁场强度与径向距离成反比,因此在靠近推力器放电通道内、外壁面处的磁场相对较大,在通道中间磁场相对较小,如图4(b)所示.为了研究径向磁场分布对推力器性能的影响,在保证轴向磁场分布B(z)和Bei大小不变的情况下,比较了3 种径向磁场分布对推力器性能的影响.

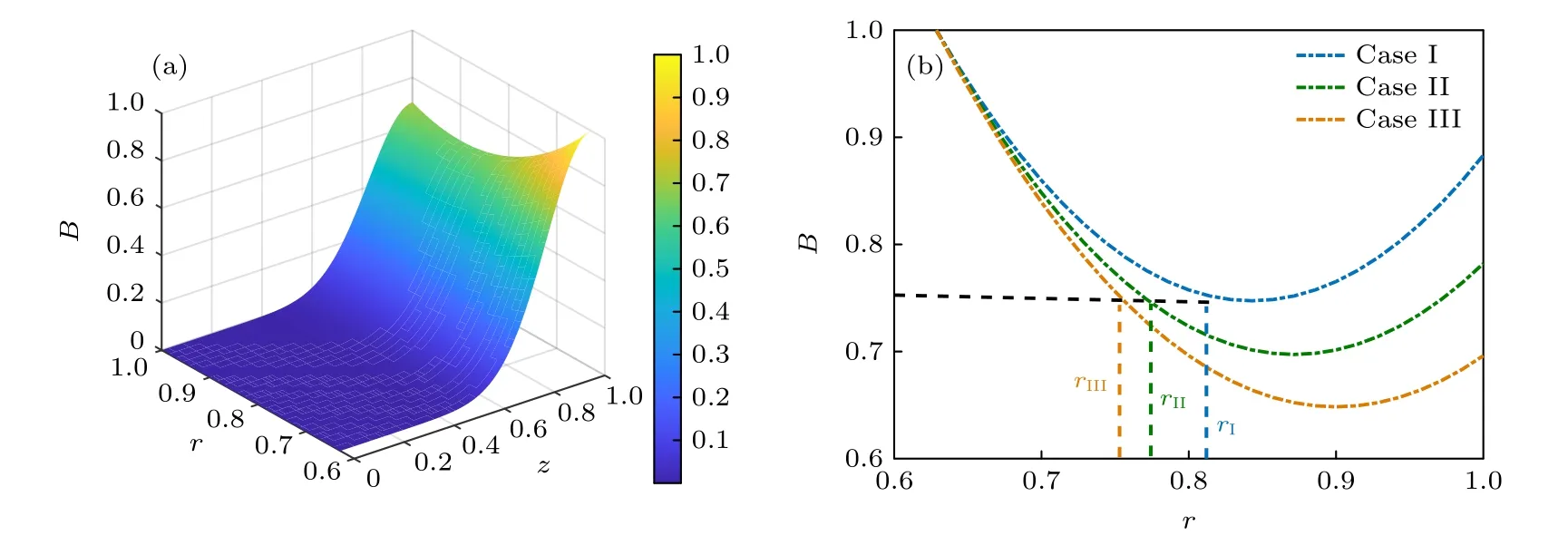
图4 (a)放电通道内磁场分布;(b)推力器出口处的径向磁场分布Fig.4.(a) The magnetic field distribution in discharge channel;(b) radial distribution of magnetic field at thruster exit.

当径向磁场不为常数时的推力和比冲如图5所示.结果表明,当Bei一定时,推力和比冲随着Beo减小而增加.当磁场剖面为“case I”时,推力平均值为=26.3 mN ,比冲平均值为=1604 s;当磁场剖面为“case II”时II=29.18 mN,=1638 s ;当磁场剖面为“case III”时III=33.5 mN,=1680 s.

图6 为磁场分布分别为“case I”、“case II”、“case III”时推力器放电通道内离子密度和电子温度的分布.当Bei=B0时,通道内离子数密度和通道出口附近的电子温度随着Beo减小单调增加,这意味着位于推力器出口附近的电场强度随着Beo的减小而增加.这是由于径向磁场分布从“case I”变到“case III”的过程中,靠近通道内壁侧的径向磁场梯度逐渐增加,即同一径向位置处的磁场强度依次减小(图4(b)所示).根据Harvey 等[29]的研究结果:磁场强度一定的情况下,加速区的电势随着径向距离的增加而减小.因此,在径向磁场从“case I”变化到“case III”的过程中,同一径向位置处的加速电势依次增加,从而使推力单调增加,如图5 所示.径向磁场改变引起推力变化的另一个可能原因是弯曲磁力线产生的磁镜效应发生了变化.霍尔推力器中弯曲的磁场会使磁力线在壁面附近汇聚,造成通道壁面处磁场强度大于通道中心的磁场强度,这将产生磁镜效应.磁镜效应能够有效约束等离子体.此外,由于环形通道效应,导致磁场强度沿半径增大的方向减小.这两个因素耦合在一起造成内壁面的磁镜效应远大于外壁面的磁镜效应.定义磁镜比ℑm=Bi/Bc,Bi和Bc分别为通道内壁面和通道中心的磁场强度.随着磁镜比的增加,磁镜效应对电子束缚能力增强,电子沿着轴向的迁移率减小,电子密度分布更加集中.在径向磁场分布从“case I”变化到“case III”的过程中,磁镜比逐渐增加,电子横越磁力线的迁移率逐渐减小,加速区长度变短,加速电场变大,离子沿着轴向漂移到达推力器出口的能量增加,推力器性能得到提升.

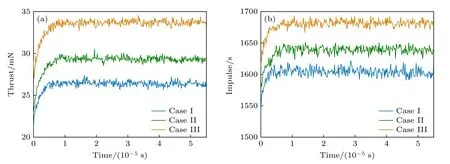
图5 (a)推力和(b)比冲Fig.5.The (a) thrust and (b) specific impulse.

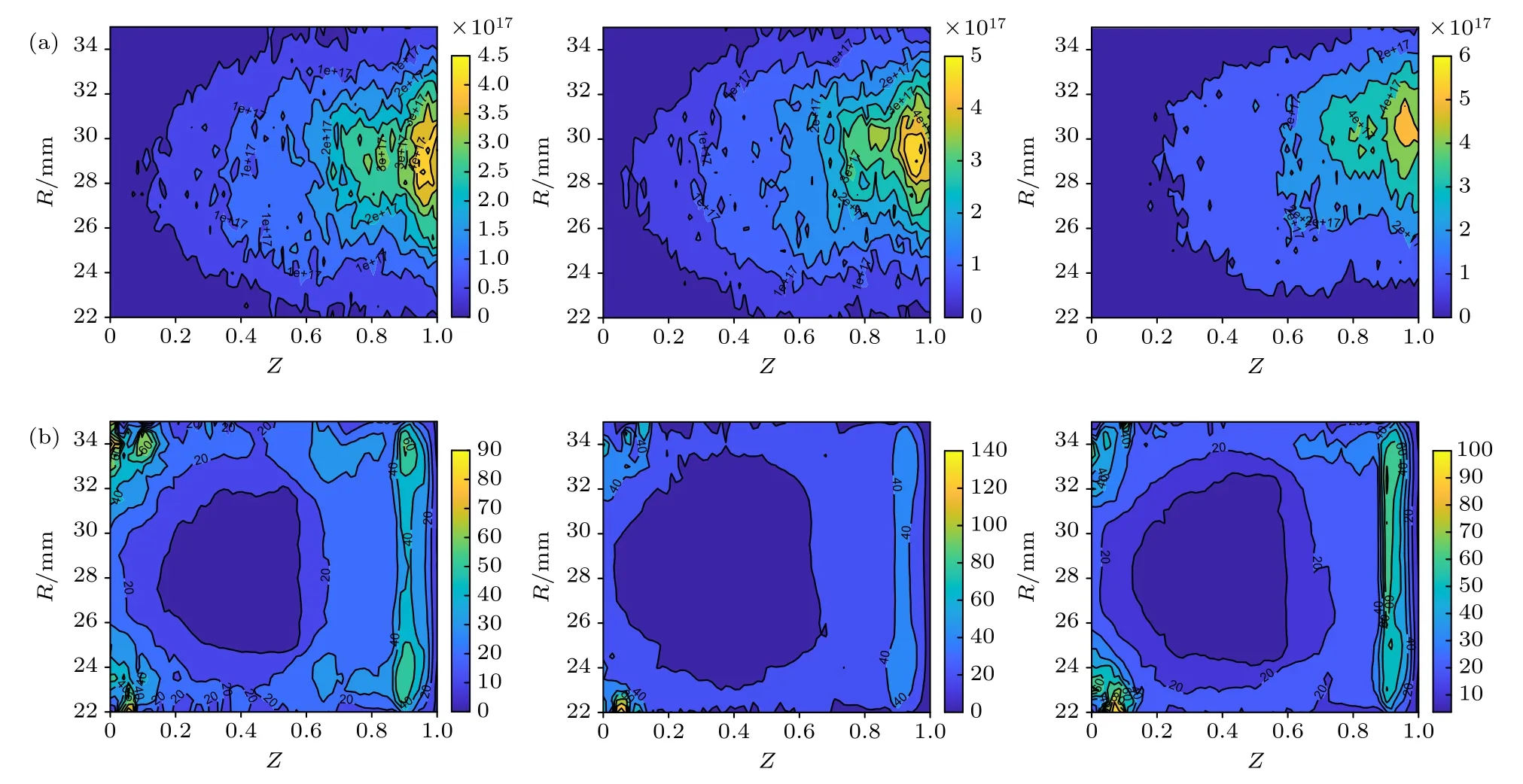
图6 (a)离子密度和(b)电子温度Fig.6.The (a) ion density and (b) electron temperature.

图7 是放电通道内中性原子密度和离子密度径向平均值沿着轴向的分布.为了比较不同径向磁场分布的影响,图中给出了径向磁场为常数时的结果(红色实线).在径向磁场分布从“case I”变化到“case III”的过程中,推力器出口处的离子数密度单调增加,原子数密度单调减小.此外,在径向磁场强度为常数B0时的离子密度和中性原子密度分布与磁场为“case II”的情况接近,因此对应的推力和比冲几乎一致.在工质流率和放电参数不变的情况下,出口处中性原子密度的减少意味着工质利用率的提高.径向磁场变化导致工质利用率提高的可能原因是:径向磁场的改变引起放电通道内加速区的电势沿着径向发生变化(磁场强度一定时,加速区的电势随着径向距离的增加而减小).径向磁场分布从“case I”变化到“case III”的过程中,同一磁场强度大小所对应的径向距离依次减小(图4(b)所示:rI>rII>rIII),加速区的电势依次增加,使得进入放电通道内的电子有足够的能量与中性原子发生有效电离碰撞.

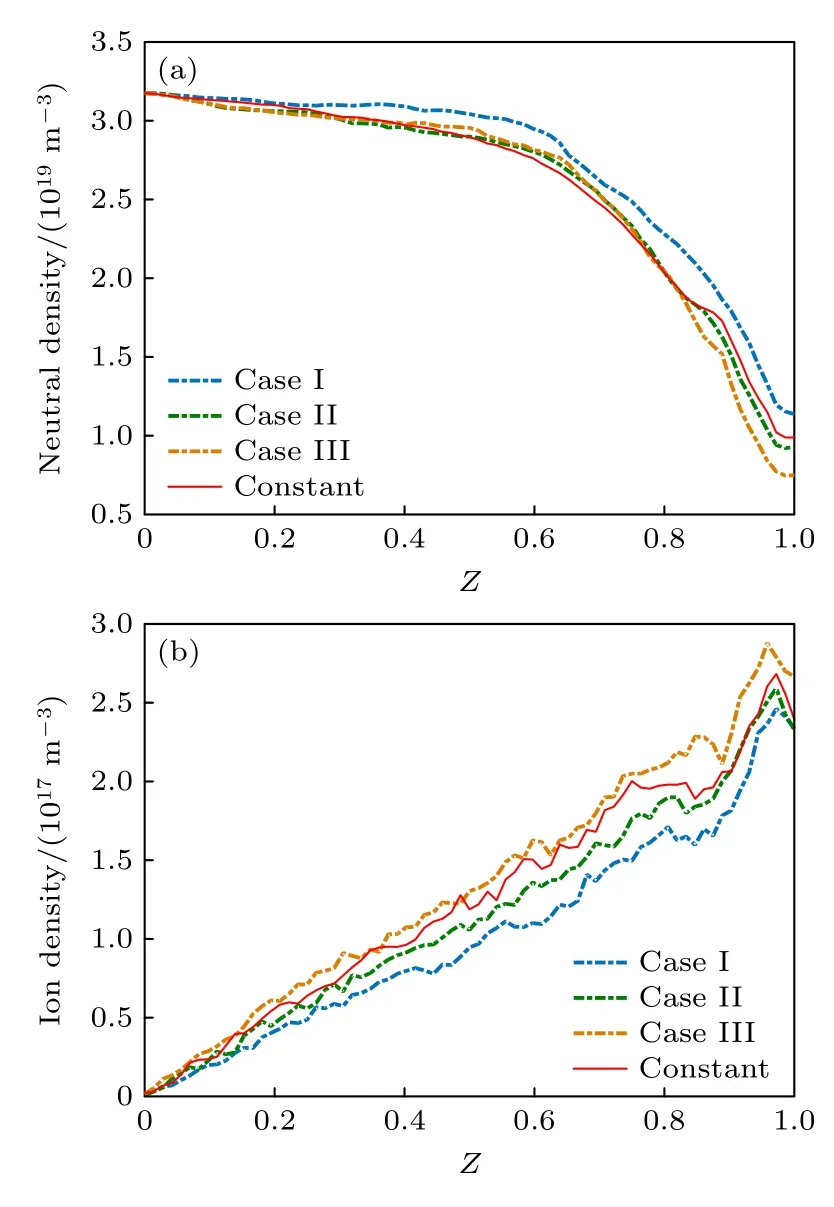
图7 (a)中性原子密度和(b)离子密度Fig.7.The (a) neutral atom density and (b) ion density.

4 结果和讨论

前面一节的结果表明,霍尔推力器中径向磁场分布对推力器性能有显著影响.本节通过理论分析进一步解释径向磁场对推力器性能影响的原因.在忽略电子沿E×B方向的惯性项后,沿霍尔推力器放电通道轴向的电子动量平衡方程可以写成如下的形式[30,31]

假设霍尔推力器中沿着E×B方向的电子电流为常数,且沿着磁场方向不存在电流,(12)式则可以写成如下的形式

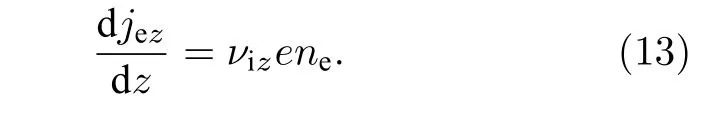
需要说明的是,这里只考虑径向磁场对放电通道内加速区等离子体的影响,因此上述方程中没有考虑电势满足的泊松方程.假定加速区的等离子体满足准中性条件,即ne=ni.在电子压强足够小,且离子电流超过电子电流时,则可以认为离子电流ji=nieυi为常数[30].用ji0表示推力器出口处的离子电流,则可得电子密度与离子电流之间的关系[30]

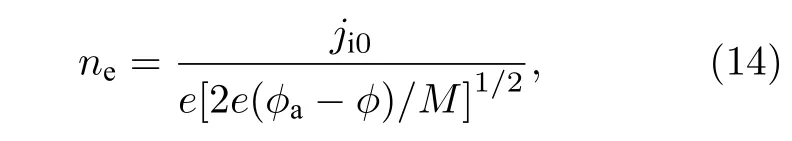
式中,φa为阳极电势,M为离子质量.假定电子从放电通道出口到阳极的过程中能量线性增加,即电子能量与电势之间满足如下关系

式中,β的变化范围为0 到1.对(11)式、(13)—(15)式进行整理并利用如下关系式做无量纲处理[31]

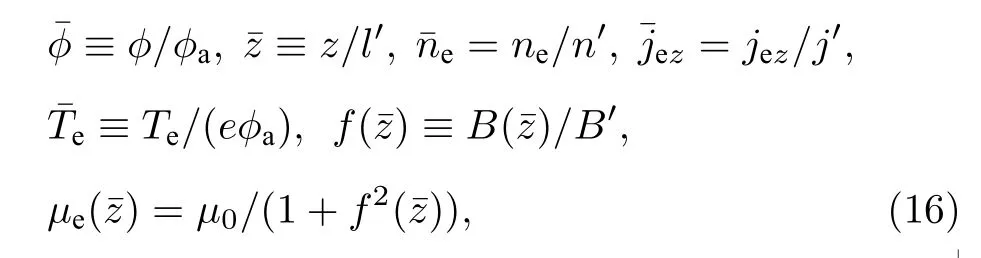
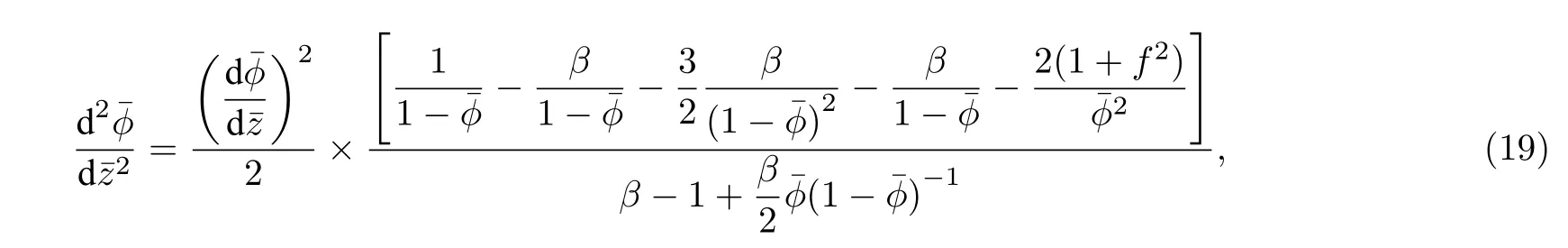
通过(19)式的求解可得加速区电势与磁场强度的关系.

图8 是不同磁场强度下加速区电势沿着轴向的变化.f表示经归一化处理后的磁场强度((16)式所示),f越大对应的磁场强度越大.横坐标表示沿着推力器出口到阳极的轴向位置.表示推力器出口的位置,表示放电通道内等离子体电势与阳极电势相等的位置,则加速区的长度可以表示为.从图中可以看到加速区电势在轴向上的变化趋势与磁场强度有很强的依赖关系:磁场强度越大,加速电势变化越急剧.对于霍尔推力器,在磁场强度B较大时,Pederson 电子迁移率µe反比于B2,加速区的长度LA∝1/B,即磁场强度越大,加速区越短[29].Kornberg[31]认为磁场的平均值影响加速区的长度,而加速区长度的改变又影响带电粒子的能量和动量.

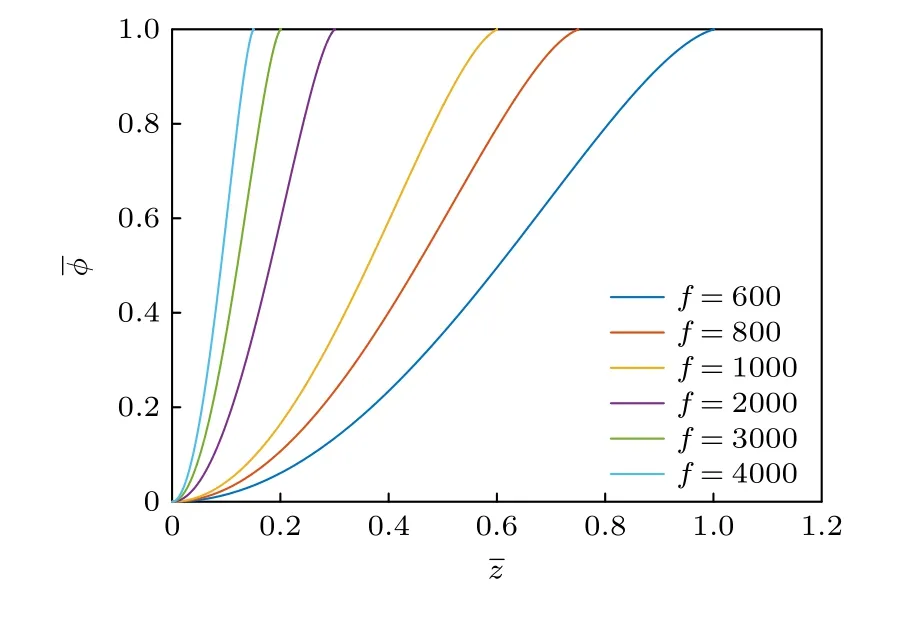
图8 不同磁场强度下的电势沿着轴向的变化Fig.8.Electric potential along the axial direction plotted for different magnetic strength.

图9 是磁场强度一定的情况下,不同径向位置r处,霍尔推力器放电通道内加速区电势沿着轴向的变化.R1为放电通道内半径,R2为放电通道外半径,从R1到R2的变化过程中,径向距离r逐渐增加.图中表明,在同一轴向位置处电势随着径向距离r的增加而减小.在磁场强度一定的情况下,假定轴向电势满足线性关系φ ≈zφa/L.在放电通道内壁R1处的磁场强度为B1,对应霍尔参数为Ω1,加速区长度为(ℓ为常数),加速区电势为φmax=φa时,则加速区的电势与径向距离满足关系[29]

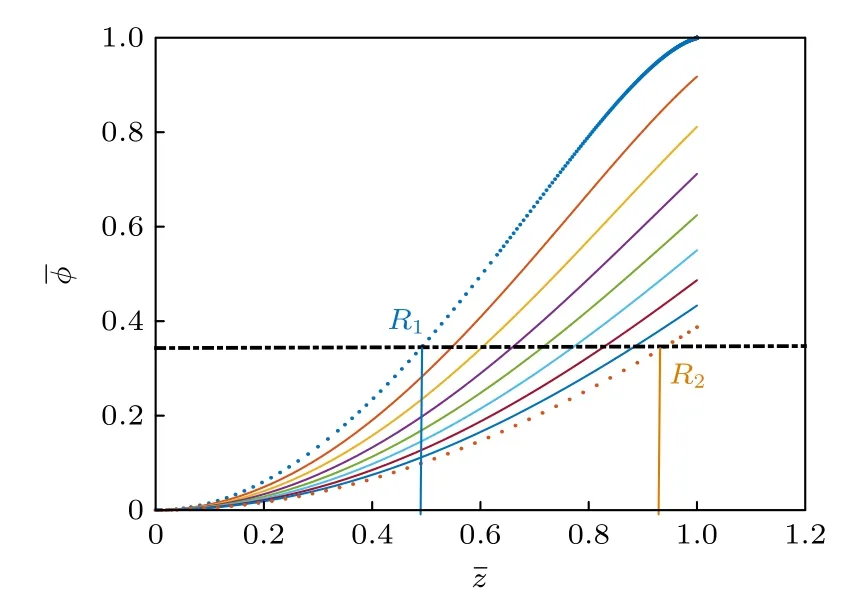
图9 不同径向位置处电势沿着轴向的变化Fig.9.Electric potential along the axial direction plotted at various radii.

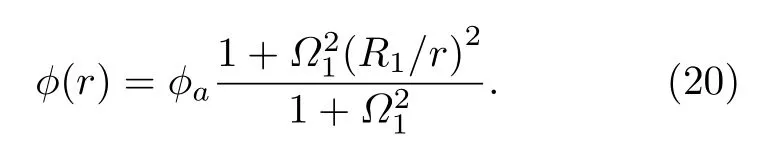
(20)式表明,随着径向距离r的增加加速区的电势逐渐减小.这意味着靠近放电通道内壁处沿轴向漂移的离子在到达推力器出口处的能量大于外壁处沿轴向漂移的离子能量[29],这一结论与数值模拟的结果定性一致.因此,在霍尔推力器中径向磁场强度相同的情况下,径向距离越小,对应的加速电势越大,离子沿着轴向漂移到达推力器出口处的能量越大,推力器的推力和比冲越高.

5 结论

本文利用粒子-流体二维混合程序数值研究了霍尔推力器中的径向磁场分布对推力器性能的影响,为了便于比较,文中同时给出了径向磁场为常数时的结果.数值结果表明,在轴向磁场不变的情况下,改变径向磁场分布将对推力器的性能产生重要的影响.具体而言,在径向磁场强度一定的情况下,推力器加速区的电势和沿着轴向漂移到达推力器出口的离子能量随着径向距离的增加而减小.因此,在径向磁场强度一定的情况下,靠近推力器放电通道内壁侧的磁场梯度越大,推力越大.本文的研究结论将为霍尔推力器磁场的设计和性能的优化提供理论支撑.