射电望远镜伺服系统的参数辨识与模型降阶∗

杨 垒，刘志勇，王 娜†，李 宁

(1.中国科学院 新疆天文台，新疆 乌鲁木齐 830011；2.中国科学院大学，北京 100049)

0 引言

大口径、高频段是现代射电望远镜的一个发展趋势.随着望远镜观测频段的提高，望远镜需要具有更高的指向精度来满足天文观测需求；随着天线口径的增大，天线的主谐振频率减小，降低了系统的响应速度，影响射电望远镜的跟踪速度.现有的射电望远镜伺服控制系统的控制算法主要是基于比例积分微分（Proportional Integral Derivative,PID）控制算法，其控制性能满足中小口径射电望远镜在中低频率的射电天文观测需求.然而，对于大口径、高频段的射电望远镜，其指向精度要求更高，而系统中的噪声（如传感器测量噪声）、外界干扰（如阵风）和天线柔性结构变形等会影响射电望远镜的跟踪性能和指向精度，使用现有PID控制算法难以满足高精度伺服控制需求.相比于PID控制算法，基于模型的控制算法，如线性二次型高斯（Linear Quadratic Gaussian,LQG）、H∞等，可以提高射电望远镜在复杂环境下的指向精度、跟踪精度和抗扰性能[1]，实现更高精度的控制.

系统建模是应用基于系统模型的先进控制算法的首要步骤.目前国内外学者对天线伺服系统模型的辨识方法开展了大量研究，并取得了很好的效果.Ranka等[2]采用扫频信号作为美国GBT（Green Bank Telescope）的输入信号，用观测器/卡尔曼滤波辨识算法得到系统位置开环模型和速度闭环模型，并用于鲁棒控制器设计；夏培培等[3]采用扫频信号作为2 m望远镜消旋K镜转台的输入信号，并运用基于Hankel矩阵奇异值的特征系统实现算法辨识出具有均衡代表性的参数模型；王昊等[4]把白噪声作为光电跟踪转台的输入信号，并利用特征系统实现算法得到其控制系统模型.然而，扫频信号作为激励信号时，辨识实验需要反复测量多个频率点，增加了系统的实验周期；由于白噪声为随机信号，系统重复测量的结果不一致，并且白噪声不易产生，其实际应用受到一定的限制[5].朱启昌[6]采用伪随机序列（Pseudo Random Binary Sequence,PRBS）作为天线伺服控制实验平台的输入信号，利用子空间辨识方法得到系统的模型；Wen等[7]采用PRBS作为车载雷达天线的输入信号，并运用相关分析法和最小实现方法得到其柔性结构的状态空间表达式.

特征系统实现算法具有详细的理论分析过程，辨识得到的是系统的模态参数，有利于简化模型降阶过程[8].本文在已有研究的基础上，采用伪随机序列（PRBS）作为系统的输入信号，运用由相关分析法和特征系统实现算法组成的辨识方法对系统输入、输出数据进行分析与处理，得到系统的模态参数，利用频域加权平衡截断法和零极点对消方法对传递函数进行降阶分析，最后通过新疆天文台南山26米射电望远镜平台开展建模实验并予以验证.

1 射电望远镜伺服系统结构

全可动射电望远镜伺服控制系统由控制器、伺服驱动系统、天线结构和量测装置四部分组成.其伺服控制系统包含方位轴和俯仰轴两个子系统，两个子系统使用多电机协调控制并且采用三环制，即电流环、速度环和位置环，其系统如图1所示.射电望远镜的结构复杂、转动惯量大、系统模态复杂、谐振频率低，并且望远镜伺服控制系统容易受到工作状况变动、天气等外部扰动[9]和内部结构的影响，基于机理分析得到的系统模型与望远镜在实际运行过程中的状态存在一定的差别，需要对望远镜进行现场模型辨识，得到能够准确描述望远镜动态特性的模型.

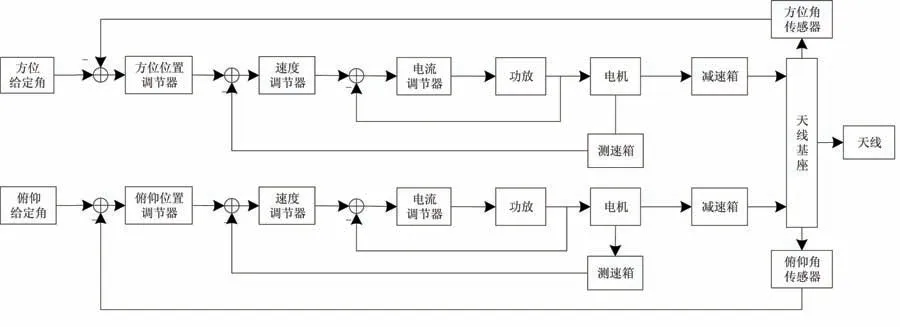
图1 射电望远镜伺服系统方框图

2 辨识算法与模型降阶方法

对射电望远镜伺服系统的现场辨识实验，可以得到天线伺服系统动态特性的数学模型，为基于系统模型的控制算法提供设计依据.通过模型降阶方法简化其数学模型，能够简化控制器的设计，有利于控制器的工程应用.下面首先介绍得到系统脉冲响应序列的方法，其次分析如何从脉冲响应序列组成的Hankel矩阵得到系统的状态空间模型，最后对模型降阶方法进行必要的描述.

2.1 脉冲响应序列与系统阶次

系统脉冲响应是指在脉冲信号作用下系统的输出响应.工程上输入理想脉冲信号并不可能，经常采用矩形脉冲进行代替，但会带来一定的误差.本文采用一种间接的方法来得到系统的脉冲响应序列.PRBS是具有近似白噪声性质的周期信号，因此采用PRBS作为输入信号激励天线系统的动态特性，并采集系统的输出信号，用x(k),y(k)分别表示输入、输出数据，其中k=0,1,2,···∞，并用g(k)表示离散系统的脉冲响应.输入信号即PRBS信号的自相关函数[10]为

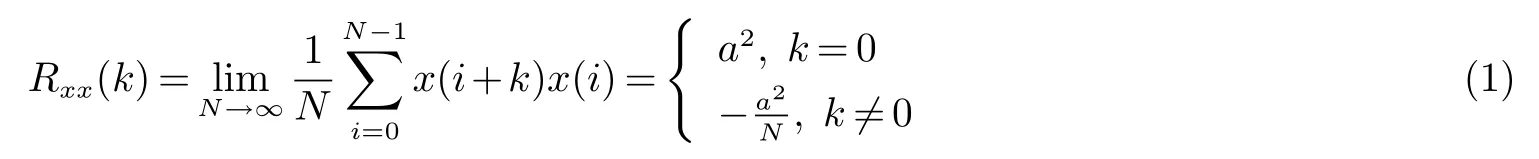
其中：a为信号的幅值，N为采集信号的长度，k为时刻.不考虑系统因果性，输出信号可由输入信号和脉冲响应表示为输入输出信号的互相关函数[11]为

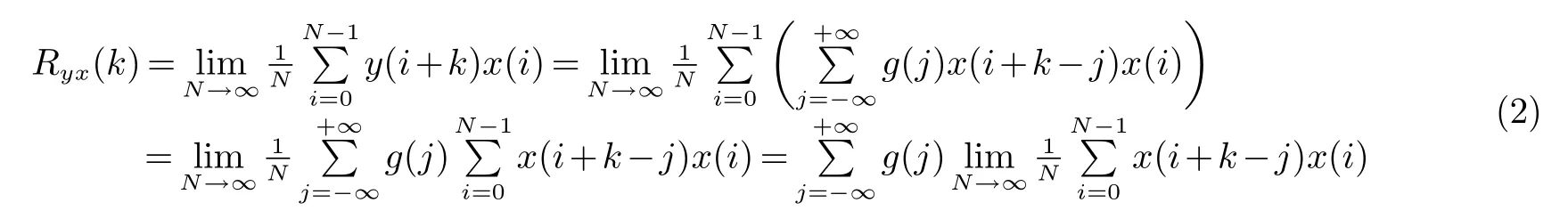
由式（1）、式（2）可知，式（2）右半部分为输入信号的自相关函数.由控制系统的因果性可知，在零时刻之前系统的脉冲响应为0，因此式（2）可转换为

由式（3）可得脉冲响应为

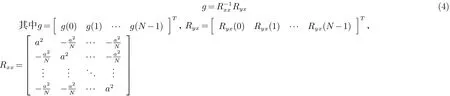
假设控制系统的离散传递函数为G(z)，g(k)为系统脉冲响应序列，则系统的传递函数和脉冲响应函数的关系为

设稳定的离散线性时不变系统的状态空间表达式为

其中：A为n×n的系统矩阵，B为n×p的输入矩阵，C为m×n的输出矩阵，D为m×p的直接输出矩阵，x(k)为n×1的状态向量，包含n个变量，y(k)为m×1的输出向量，包含m个变量，u(k)为p×1的输入向量，包含p个变量.则离散传递函数为

由泰勒公式展开式可知

则式（7）可转换为

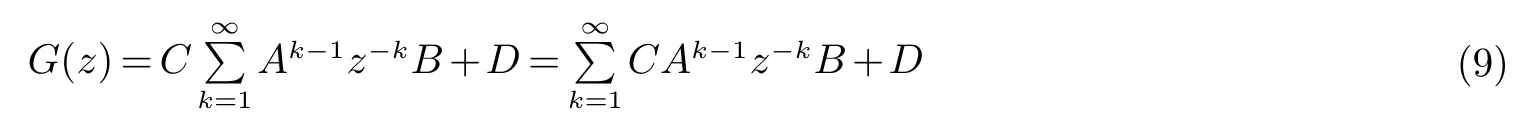
把式（9）与式（5）相比较，可得系统的脉冲响应为

由以上分析，得到系统脉冲响应序列与系统的状态空间表达式(A,B,C,D)之间的关系.利用脉冲响应序列构造广义Hankel矩阵

矩阵的奇异值代表了每一个相应模态的重要性，依据奇异值大小来选取对系统影响较大的模态，舍弃对系统影响较小的模态，以此来确定系统的阶次.

2.2 特征系统实现算法

特征系统实现算法是一种基于状态空间的时域模态参数识别方法，利用系统脉冲响应序列得到系统的最小实现[10,12].

由前文可得系统的Hankel矩阵与状态空间表达式之间的关系，并运用奇异值分解得到了系统的阶次，在此基础上基于特征系统实现算法得到系统的参数.

在式（12）的基础上设矩阵H+，使得QH+P=I，则

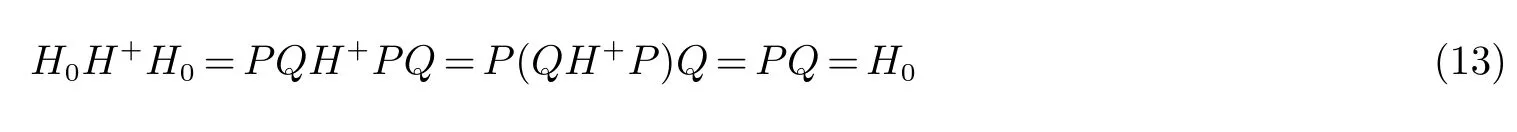
将式（15）与式（10）相比较，得到辨识模型的参数为

2.3 模型降阶方法分析

通过系统辨识得到的传递函数可以准确地描述射电望远镜伺服控制系统的动态特性，但该传递函数阶次过高，设计出的控制器阶次也会相对较高，不利于工程的应用，因此要通过模型降阶方法得到一个与原系统有近似响应特性的低阶模型.

模型降阶的方法有很多种，比较成熟的经典方法有Krylov子空间类方法、平衡截断法、多点拟合方法和正交分解降阶方法等，蒋耀林教授对此进行了详细的描述[13].本文采用频域加权平衡截断法与零极点简化法来对辨识模型进行降阶.

频域加权平衡截断法是指在一个特定频域内利用平衡截断法对原系统进行降阶[14].设n阶被控对象

是一个平衡实现，其中A1,B1,C1为被控对象相应的常数矩阵.m阶输入加权函数为

其中：Ai,Bi,Ci为加权函数相应的常数矩阵.则存在唯一矩阵Γ ∈Rn×m和对称矩阵P满足

基于输入加权函数的频域加权平衡截断法具体的设计步骤[15]：

（1）求解公式（19）得到矩阵Γ和P；

（2）得到能够满足公式（20）的转换矩阵T

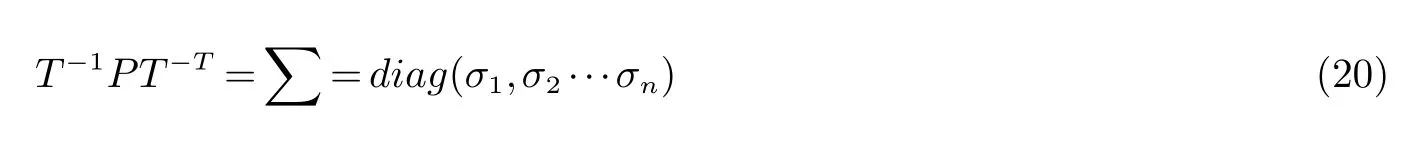
其中：σ1≥σ2≥···≥σn＞0；

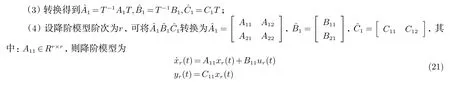
零极点简化是通过分析系统零极点分布情况，对消或近似对消零极点得到简化模型.

3 实验测试与分析

为了验证本文所提辨识方法的有效性，以南山26米射电望远镜为实验平台开展相应的辨识实验.由天线主谐振频率与天线口径的近似计算公式[16]可知，26米天线伺服系统的主谐振峰在2 Hz附近.南山26米射电望远镜伺服系统的采样频率为20 Hz，依据香农采样定理可知，采集的数据能够描述系统频域10 Hz以内的频率特性.

3.1 系统频域测试与数据分析

实验过程中首先断开26米射电望远镜伺服控制的位置环控制器，选择阶次为10阶、幅值为0.5的PRBS信号作为其速度输入信号.采集望远镜位置编码器信号，并对所采集信号做差分处理，得到系统的实际速度.然后对输入、输出信号进行离散傅里叶变换，得到望远镜伺服系统速度环的幅频特性.再用[0,5 Hz]的扫频信号作为激励信号，采集输入、输出数据，用于对比验证辨识实验的有效性.两者的幅频特性如图2所示，由图2可知两者在扫频信号频率范围内的频谱特性基本相似.在[5 Hz,10 Hz]频域范围内，扫频信号的幅值很小，而输出包含噪声和其他高频扰动信号，因此系统高频部分的幅值会变得很大.但PRBS频谱在全频段均有分布，能够得到扫频信号无法描述的高频信息.

图2 两种信号产生的输出的频域特性

在所采集的输入、输出数据中选取一个周期数据（即1 024个数据），依据公式（1）～（3）得到射电望远镜系统的脉冲响应序列.然后，选取脉冲响应序列的前50个值，根据公式（11）组成Hankel矩阵并对其进行奇异值分解，得到的奇异值大小如图3所示.由图3可知，其奇异值在第7个和第11个之后都有一个明显的变化，由此得到26米射电望远镜伺服系统模型的阶次.

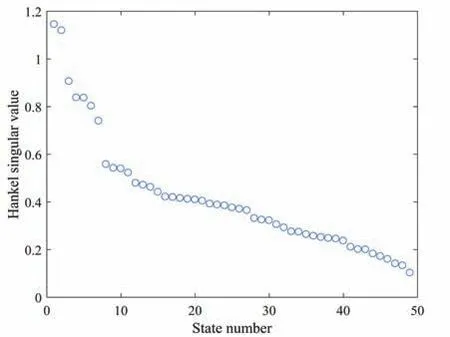
图3 Hankel矩阵奇异值

3.2 参数估计与实验方法对比分析

根据3.1节得到系统的脉冲响应序列、Hankel矩阵和模型阶次，由公式（16）得到26米射电望远镜伺服系统的7阶和11阶状态空间方程.为了对比，利用子空间辨识（Subspace Identification,SID）方法[17]对同一组数据进行了分析.

两种方法的7阶和11阶模型的伯德图与原始数据的频谱图如图4所示.由图4可知，选择7阶作为辨识模型的阶次时，本文所用辨识方法（I-H）得到的模型在低频能够准确地描述系统的前两个谐振点，而SID方法所得模型在低频只有一个谐振峰；当选择11阶时，两种辨识方法所得模型在整个频域范围内都能够与原始数据的频谱图近似拟合.为了验证本文所用方法的有效性，最终选择11阶作为系统的阶次.

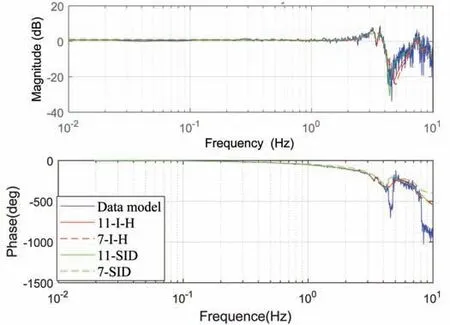
图4 I-H和SID比较

对两种辨识方法所得传递函数进行时域和频域的模型验证.在时域中，对天线自身和两种传递函数输入相同的信号，两种辨识模型输出与实际系统输出的残差平方和作为时域指标；频域指标为两种模型在幅频特性上同采样数据频谱图的残差平方和，其结果如表1所示.表1表明本文提出的辨识方法比子空间法对天线整体的动态特性的描述效果更好一些.将辨识得到的11阶状态空间方程转换成连续的传递函数如式（22）所示.

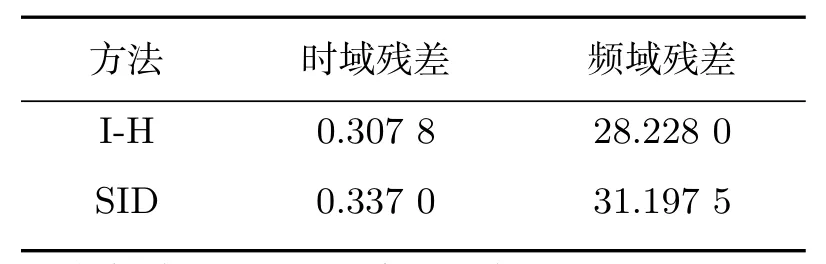
表1 两种算法的误差

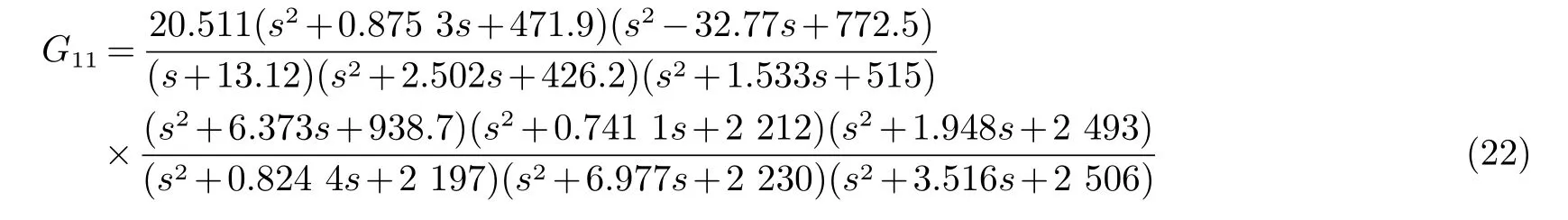
3.3 模型降阶分析

通过上述系统辨识实验得到的天线模型阶次为11阶，不利于控制器设计与应用，需要对系统模型进行简化.选取包含前两个主谐振峰的频率范围，并依据2.3节的频域加权平衡截断法对辨识模型进行简化，得到5阶模型.图5为11阶与5阶模型的阶跃响应，由图5可知，5阶模型与系统辨识的11阶传递函数的阶跃响应变化趋势基本一致，因此可把传递函数从11阶简化成5阶，其传递函数如式（23）所示.

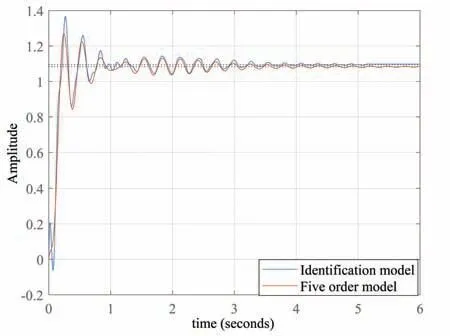
图5 阶跃响应分析

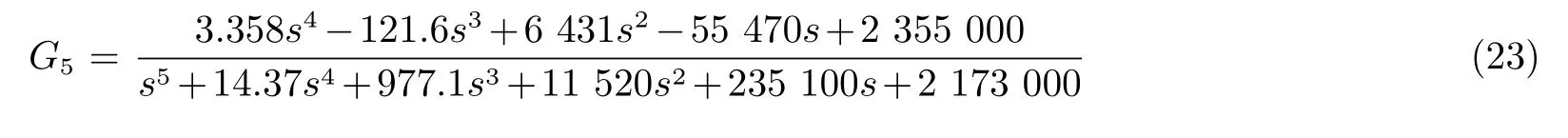
利用5阶模型设计的控制器是一个高阶控制器，不利于工程应用.根据文献[18]的简化思想，分析5阶模型的零极点分布范围，运用零极点简化方法，经过微调把5阶模型简化成2阶模型，其表达式为

三个模型的幅频特性如图6所示.由图6可知，最终简化得到的2阶模型的谐振峰包络着主谐振峰.

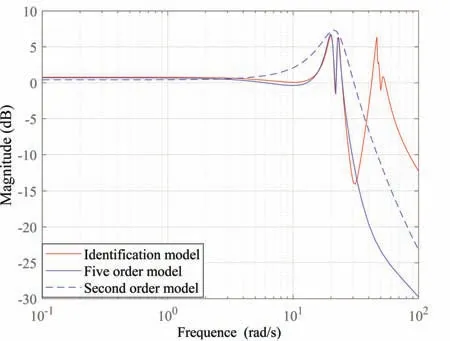
图6 三个模型幅频特性

4 结论

本文分析了一种基于相关分析法和特征系统实现算法的伺服系统辨识方法，并对南山26米射电望远镜进行了辨识实验.本文采用的辨识方法能够描述南山26米射电望远镜伺服控制系统动态特性的11阶模型.与子空间法得到的天线模型进行对比，结果显示，本文所采用的辨识方法得到的参数模型与实验数据在时域和频域中的误差更小.最后运用频域加权平衡截断法和零极点对消两种模型降阶方法，通过两次降阶将辨识得到的11阶模型简化为2阶模型.