小样本下分层双边数据相对风险比的精确检验∗

牟珂漪，李智明

(新疆大学 数学与系统科学学院，新疆 乌鲁木齐 830017)

0 引言

在临床医学实验中,当患者提供来自配对器官如眼睛、耳朵或胳膊等数据时,所有可能的结果分别为无、一个或两个响应,此类数据称为配对数据.文献[1]认为来自同一个个体的配对器官之间的响应是互相关联的,如果忽略其组内相关性,将会导致统计推断出现偏差.假定一个器官出现响应时,另一个器官也出现响应的概率是无条件概率的R倍,其中R为一个正常数,在这个假设条件下的模型称为Ronser模型.文献[2]指出Ronser模型的不足,认为一个器官出现响应的条件下,另一个器官也出现响应的概率并不依赖于无条件响应的概率.文献[3]提出Donner模型并假定每个组的相关系数是固定的.文献[4]证明Donner模型能充分利用来自单个或配对器官的数据以提高检验的功效.文献[5]将此模型用于分层的配对数据并假设各层中每一组的相关系数相同,不同层之间不同.Donner模型下更多研究结果可参阅文献[6-8].

近年来,一致性检验成为配对数据研究中的热点问题.文献[1]提出两个统计量检验独立或者非独立模型中比例差的一致性.基于此,文献[9]建立了适用于小样本或稀疏数据结构的精确和渐近方法.此外,文献[10]提出检验治愈率一致性的统计量,包括独立和非独立模型下的似然比、Score和Wald型检验等.在Rosner模型下,文献[11]提出Score和Wald型统计量检验分层双边设计中的比例差异.当样本量较大时,渐近方法下的检验具有良好表现,但当样本量相对较小时,渐近检验就难以保持良好的第一类错误率和功效.因此,除了利用渐近方法构造检验统计量外,小样本下的精确方法在配对数据上的分析同样值得关注.

在有关精确检验的研究中,文献[12]使用原假设下的极大似然估计值来替换讨厌参数,此方法被称为E方法.文献[13]通过最大化所有讨厌参数范围上的尾部概率来计算p值,称之为M方法.精确方法更多研究内容可参阅文献[14-17].然而,上述精确方法大多集中于单层多组情形,对多层两组的双边数据进行精确检验的研究较少.本文提出基于Score检验的E方法和M方法,对分层配对数据的各层相对风险比进行一致性检验,并通过拟合比较渐近方法与E方法、M方法在第一类错误率和功效下的表现.

1 Donner模型和参数估计

在配对相关数据的临床研究中,假设患者由于某种混杂因素(如年龄、性别、疾病严重程度等)被分为J层.设Mj为第j层的总人数(j=1,···,J),每层的患者被随机分入2个治疗组接受不同的治疗.令mlij为第j层第i组中带有l个响应的患者总数(l=0,1,2,i=1,2,j=1,···,J),plij分别表示第j层第i组中无、单边及双边响应的概率.对于任何固定的i和j,p0ij+p1ij+p2ij=1都成立.第j层第i组的患者总人数且各组总人数固定不变,Slj表示第j层中出现l个响应的患者总数.分层模型中第j层的数据结构如表1所示.

表1 分层配对相关数据第j层结构

记mij=(m0ij,m1ij,m2ij)T,pij=(p0ij,p1ij,p2ij)T.对于第j层,mij(i=1或2)服从三项分布.因此,mij的联合概率密度函数为

设Zhijk表示第j层第i组中第h(h=1,2,···,Nij)位患者的第k(k=1,2)只眼睛的响应变量.如果存在响应,Zhijk=1,否则为0.在Donner模型下,假设P(Zhijk=1)=πij,0 ＜πij＜1,以及Corr(Zhijk,Zhij(3−k))=ρj(0 ＜ρj＜1).故,p0ij=ρj(1-πij)+(1-ρj)(1-πij)2,p1ij=2πij(1-ρj)(1-πij),p2ij=ρjπij+(1-ρj)i=1,2,j=1,···,J.对于i=1,2,记πi=(πi1,···,πi2)T,ρ=(ρ1,···,ρJ)T.据观察数据mij(i=1,2,j=1,···,J),其对数似然函数为

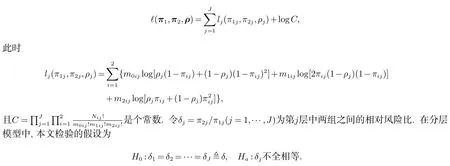
在假设H0下,π2j=π1jδ(j=1,···,J).因此其对数似然函数可以写为

其中：δ为兴趣参数,π1和ρ为讨厌参数,并有

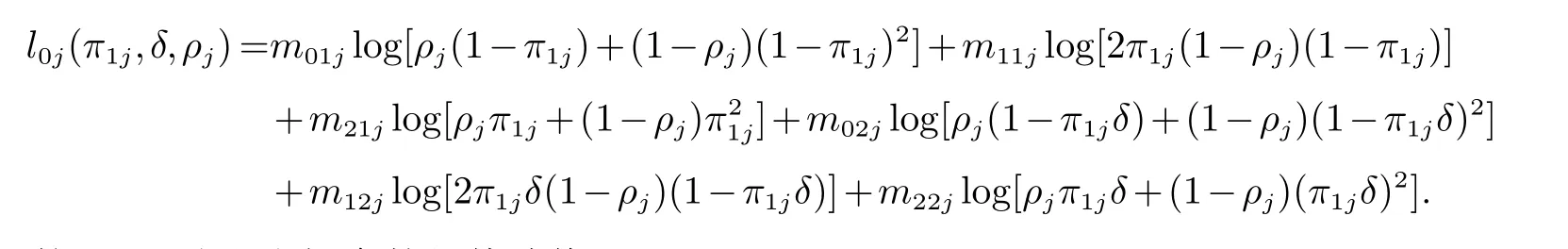
根据似然函数,下面给出未知参数的估计值.

然而,上式并不存在显式解,需要利用迭代算法如Fisher得分算法、牛顿法、Bootstrap方法等求得极大似然估计[18].针对多组配对相关数据的极大似然估计,文献[19]指出相比牛顿法和广义期望最大算法,Fisher得分算法在收敛方面具有一定优势.考虑到Bootstrap方法花费时间久,本文选择Fisher得分算法得到全局极大似然估计在Donner模型中,一共有3J个未知参数.对于第j层,πij,ρj(i=1,2)的初值设为

参数π1j,π2j以及ρj(j=1,···,J)的第t+1次迭代值可以通过Fisher得分算法求得

利用mlij(l=0,1,2,i=1,2,j=1,2,···,J)的期望可得Fisher信息矩阵中二阶偏导的期望.

在原假设H0:δ1=δ2=···=δJ≜δ下,π2j=π1jδ (j=1,···,J)成立,也就是说,所有层中的相对风险比都相等.此时,第j层中的一阶偏导式为

然而,该显式解并不存在.因此,采用Fisher得分算法获得限制性极大似然估计的初值在公式(1)中给定,且δ(0)=1.则δ,π1j和ρj(j=1,···,J)的第(t+1)次更新可以由Fisher得分算法计算得到

这里diag为对角矩阵符号.

2 检验统计量

基于Fisher得分算法得到的极大似然估计,可以构造渐近方法下的一致性检验.

2.1 Score检验

其中I2(δ,π1,ρ)是一个3J×3J信息阵.在Ha下,涉及到所有层参数的信息阵

在H0下,检验统计量TSC渐近服从自由度为J-1的卡方分布.由于该方法为渐近方法，简记为A方法.令是自由度为J-1的卡方分布的100(1-α)分位数.在显著性水平α下,如果检验统计量的值大于那么H0就应该被拒绝.

2.2 E方法

2.1节所提出的Score检验统计量当样本量较大时具有令人满意的结果,但是对于小样本量表现较差.因此,基于Score检验构造两种精确方法分别为E方法与M方法.计算精确方法下的p值,需要合适的方法确定尾部区域和处理讨厌参数.E方法由文献[20]提出,对于一个给定的样本矩阵M∗,固定各个组的总人数Nij(i=1,2,j=1,2,···,J),通过改变矩阵中各个元素的值,可以得到各组人数不变时所有可能的样本矩阵.所有统计量值大于M∗矩阵统计量值的对应矩阵组成了M∗的尾部区域:则p值为尾部区域的似然函数值总和.利用原假设H0下的极大似然估计来代替未知参数定义样本矩阵M∗对应的p值

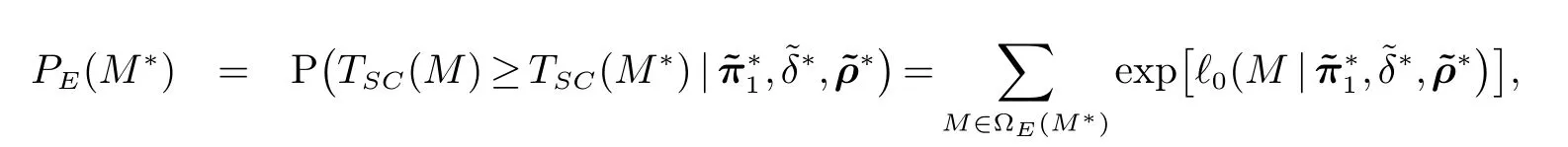
2.3 M方法

M方法由文献[21]提出,通过在定义域内任意选取参数π1,δ,ρ使得尾部区域的概率总和最大化.与E方法类似,M方法的尾部区域定义为M方法下的p值为

其中：π1=(π11,π12,···,π1J)T,ρ=(ρ1,ρ2,···,ρJ)T.

3 数值拟合

对给定参数下A方法、E方法与M方法的第一类错误率和功效进行比较.第一类错误率是当原假设为真时拒绝原假设的概率.根据文献[9],若显著性水平为0.05,第一类错误率在0.04与0.06之间时称检验为稳健的;当第一类错误率大于0.06时检验是冒进的;当第一类错误率小于0.04时检验是保守的.功效即当原假设错误时正确地拒绝原假设的概率.一个好的检验不仅要有稳健的第一类错误率,也应该有尽可能高的功效.渐近Score方法的第一类错误率和功效通过拟合得到,在原假设或备择假设下设置参数,然后在给定参数下随机生成10 000个样本.当显著性水平为0.05时,基于这10 000个样本统计p值小于0.05时拒绝原假设的次数,即可通过拒绝次数/10 000得出第一类错误率或功效.对于精确方法E方法和M方法,则需要计算每组样本量固定时所有可能样本的p值,将p值与0.05比较,统计拒绝的次数得到精确方法的第一类错误率和功效.

由于E方法和M方法需要计算每组样本量固定时所有样本矩阵所对应的p值,并将识别出的尾部区域对应似然函数值进行加总.考虑到精确方法求取第一类错误率和功效的计算量比较大,本文仅给出层数J=2时,每层中各组人数Nij=10(i=1,2)下三种方法的第一类错误率和功效.计算第一类错误率时,令πij在满足δ1=δ2=1,π11=π12的条件下随机生成,计算A、E和M方法的第一类错误率.A方法、E方法与M方法在给定参数下的第一类错误率如图1所示.图1的第一类错误率结果表明:在显著性水平α=0.05下,A方法的第一类错误率大都接近0.04,说明在小样本情形下该方法偏保守.M方法的第一类错误率比A方法低,三种方法中M方法较保守.E方法第一类错误率集中在0.04～0.06之间,且中心区域靠近0.05.说明在小样本的条件下,E方法的第一类错误率较为稳健.因此,当样本量较小时,E方法在第一类错误率方面的表现较好.

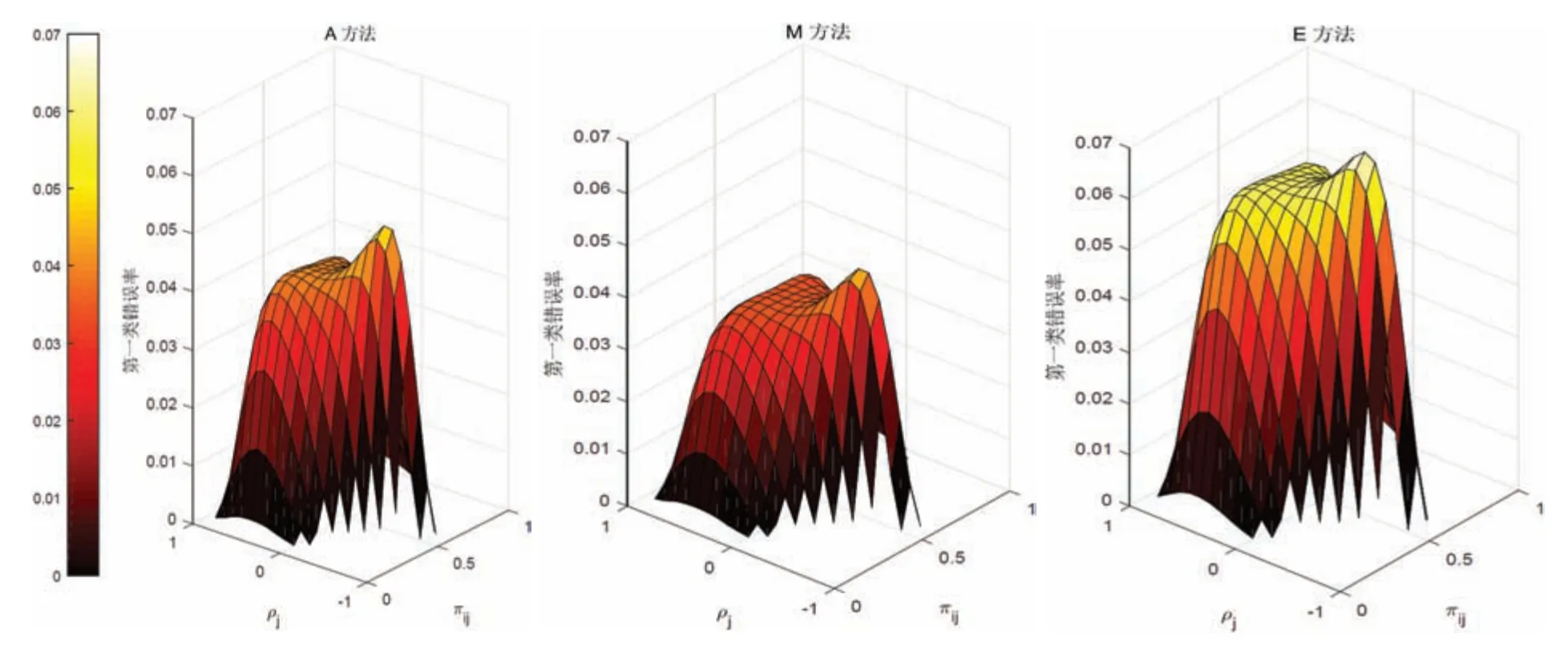
图1 A方法、M方法与E方法的第一类错误率

再比较A、E与M方法在不同参数下的功效.计算功效时,在假设Ha:δj不全相等下设置参数.对于两层的数据结构,令各层相关系数为ρ1=ρ2=0.2,0.5,0.8,且π11=π12=0.3,0.6,0.9,第一层的相对风险比为δ1=1,使第二层的相对风险比δ2以0.1为间隔,在0.1～0.9之间变动.表2显示了上述参数设置下A、M与E方法的功效,可以看出,在相同的参数设置下E方法的功效较高,M方法的功效较低.当δ1=1时,随着δ2减小,即δ2与δ1的差距增加时,三种方法的功效也会增大.中低度相关数据(ρj=0.2,0.5)下三种方法的功效往往比高度相关数据(ρj=0.8)要高.

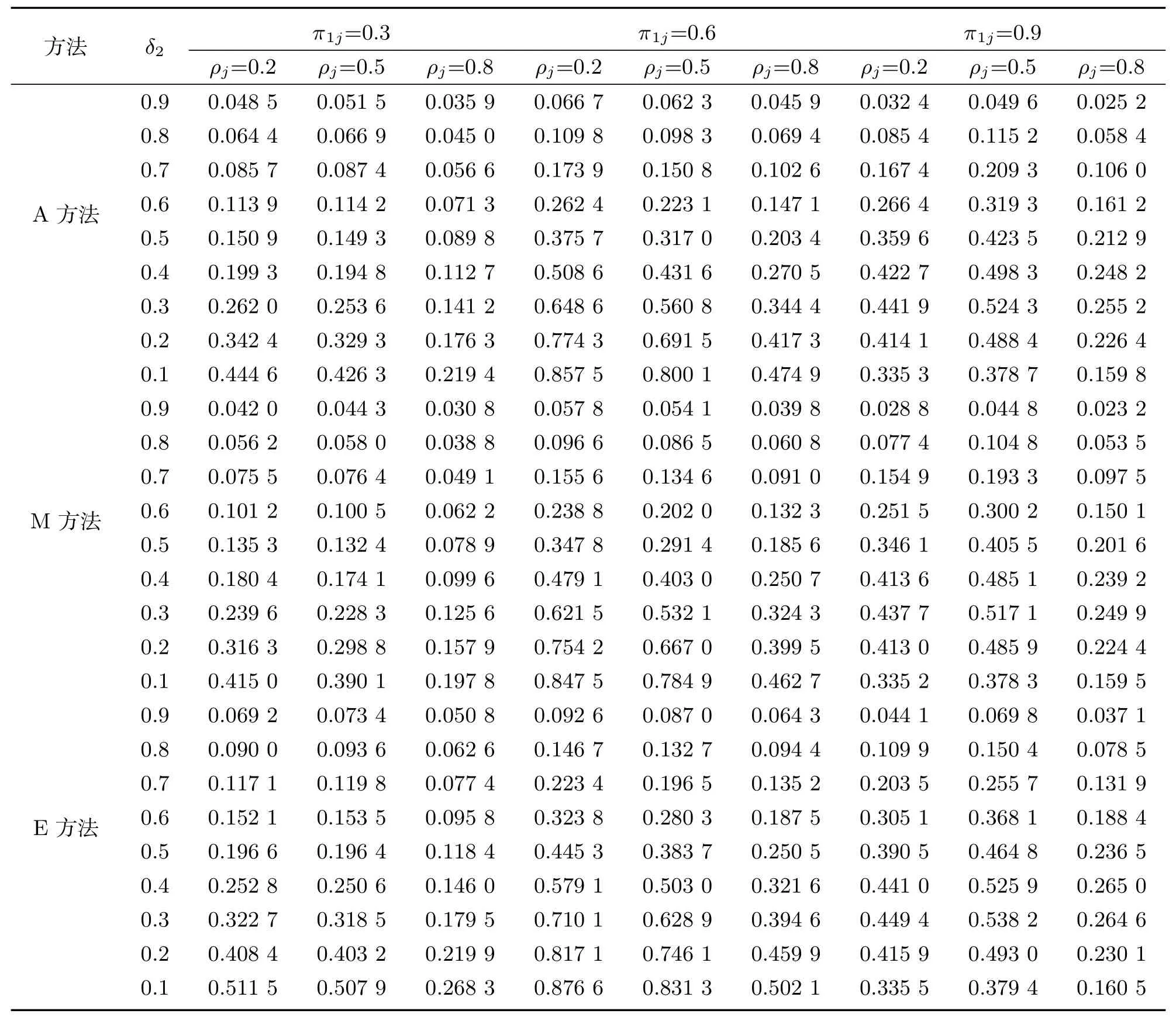
表2 A方法、M方法与E方法的功效

综合三种方法在第一类错误率和功效的表现来看,E方法较佳,因为E方法有较稳健的第一类错误率和较高的功效.因此,对于小样本下分层双边数据的相对风险比的一致性检验,推荐使用E方法.

4 结论与展望

在Donner模型下利用Score检验推导出两种适用于小样本分层双边数据相对风险比一致性检验的精确方法,分别为E方法和M方法.通过拟合比较渐近Score方法、E方法与M方法的第一类错误率和功效,表明E方法有较为稳健的第一类错误率,其他两种方法的第一类错误率偏保守.在功效方面,E方法的功效较高.综合来看,对于分层双边数据小样本下的一致性检验,推荐E方法.由于层数过多将带来巨大的计算量,本文仅提供了三种方法在两层设计中给定参数下的第一类错误率和功效,当层数大于两层时,精确方法的表现还值得进一步研究.