钢结构桥梁桥面负荷强度可靠性预测模型的构建及应用

王文建，王聪

（中国市政工程西南设计研究总院有限公司，成都 610000）

1 引言

随着城市建设速度的加快，对城市空间结构提出了较高要求。面对强大的地面交通压力，如何在有限的空间内设计一套高负荷强度桥面的桥梁方案，成为当前重点研究内容[1]。负荷强度可靠性预测作为桥梁方案成功的关键，其预测精度成为成功的关键。目前，钢结构桥梁是城市轨道交通的主要建设项目，如果负荷强度过大，可能导致轨道交通的线路平顺性能下降[2]。如果可以控制好负荷强度，便可以为桥面施工中的不均匀沉降控制提供可靠参考依据。由于当前关于钢结构桥梁的桥面负荷强度可靠性的预测研究较少，尚未形成完整的预测模型[3]。本文尝试引入双曲线算法、遗传算法，提出新的负荷强度预测模型研究。

2 钢结构桥梁桥面负荷强度可靠性预测原理

负荷强度可靠性预测采用“三点法”展开计算分析，以时间与负荷强度作为主要指标，对两项指标的关系组合表达式进行拟合，从中得出预测结果。

假设钢结构桥梁桥面施工产生的负荷强度为Qcc，瞬时施工负荷强度为Qd，施工实际测量数据拟合系数为α 和β。一般情况下，α=8/π。运用“三点法”构建负荷强度预测模型：

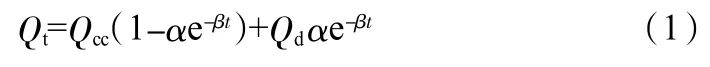
式中，Qt为时间点t 对应的负荷强度。

整理桥梁施工实际数据，生成荷载-时间（Q-t）曲线，选取施工加载操作后的3 个时间点，分别为t1、t2、t3，3 个时间的时间间隔相同，满足关系t2-t1=t3-t2。加载完成后，尽可能延长时间间隔。其中，Q-t 曲线末端选取时间t3。

依据太沙基固结理论，对上述模型中的各项参数进行整合，可以得到固结度Pt计算方法，公式如式（2）：

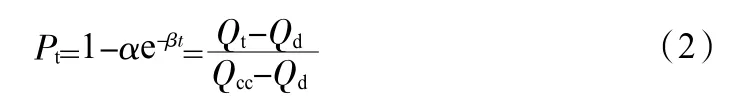
根据式（2），可以计算桥面施工期间产生的负荷强度数值，计算公式如式（3）：

式中，Q1代表时间点t1对应的负荷强度；Q2代表时间点t2对应的负荷强度；Q3代表时间点t3对应的负荷强度。

整理上述公式，计算参数Q1、Q2、Q1、α 和β，并将计算结果代入式（1）和式（3）中，得到瞬间负荷强度Qd，经过推理还可以得到最终负荷强度为Qcc。其中，参数β 的计算式如式（4）：

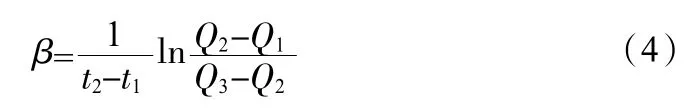
采用上述方法计算得到的最终负荷强度Qcc，作为桥面负荷预测结果。按照此计算原理，可以对桥面负荷强度可靠性展开全面预测，作为研究理论基础。

3 钢结构桥梁桥面负荷强度可靠性预测模型的构建

考虑到桥面沉降影响因素较多，为了得到较为可靠的负荷强度预测结果，从具备变异性的随机变量中挑选出性能较为特殊的变量作为重点研究对象。例如，支护参数、地层参数、注浆参数等。根据各个变量之间的关系，得到式（5）所示关系式：

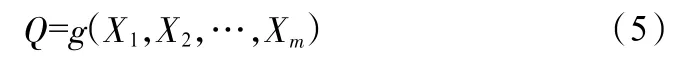
式中，Q 为负荷强度；g 为沉降影响因素系数；X=（X1，X2，…，Xm）为施工期间产生的负荷强度；m 为沉降影响因素数量。

利用式（5）可以得到差异沉降最大能力，从而掌握相关因素对桥梁结构抗力的影响，根据影响情况，描述沉降功能函数，计算公式如式（6）：

式中，Z 为沉降功能函数；R 为结构抗力。

利用公式（6）计算桥面负荷强度是否满足标准，从而判断当前桥面可靠性。如果计算结果Z 大于0，则认为桥面负荷强度可靠；如果Z 等于0，则当前桥面达到了极限状态；如果Z小于0，则当前桥面为失效状态，不可靠。

目前，关于桥面可靠性预测模型存在很多不足之处，预测结果存在较大提升空间。本文采用概率分析思想，引入双曲线算法、遗传算法，构建一种可靠性较高的负荷预测方法。

假设桥梁施工时间为t，在此时间范围内施工沉降总量为Wt，当t 为0 时，负荷强度最初值为W0，负荷强度固定条件下的回归系数为a 和b。利用双曲线模型预测负荷强度，式（8）和式（9）为计算公式：

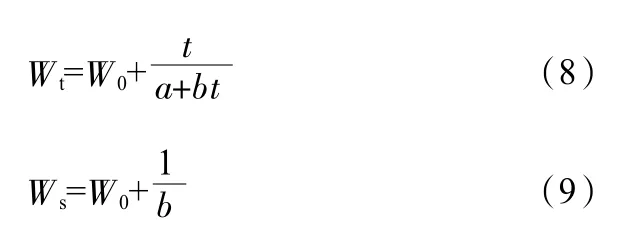
式中，Ws为桥面施工期间负荷强度最终数值。

为了提高计算灵活性，本研究引入遗传算法，随机抽取变量定义域来确定初始种群，而后与双曲线函数结合，共同描述负荷强度衰减规律。计算公式如式（10）和式（11）：

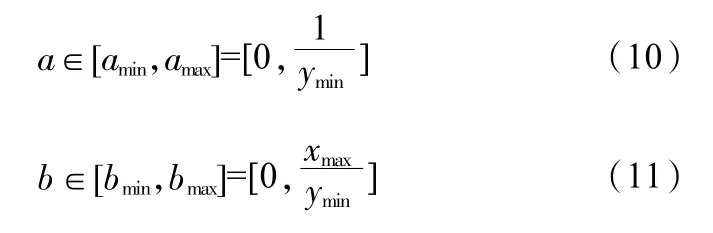
式中，xmax为时间相关自变量集合中的最大值；ymin为桥面施工期间产生的负荷强度相关因变量集合中的最小值。运用这两个公式计算所得结果，将作为负荷强度最佳系数确定参考依据。

按照上述求解思路，设计以下负荷强度目标函数的求解步骤：

第一步：初始化设置。确定函数相关参数，完成种群设置。例如，钢结构桥梁桥面种群规模，记为n；函数交叉概率，记为pc；染色体长度，记为L；函数变异概率，记为pm。在确定这些参数以后，构建负荷强度可控性预测模型，以函数S1来描述，式（12）为计算公式：

式中，si为负荷强度个体适应度函数。

第二步：按照交叉概率pc标准，分析施工期间桥面的负荷强度变化规律，确定交叉个体。通过大规模搜索分析，计算种群中的变异概率。为了得到负荷强度种群新个体，采用基因突变方法加以处理，最终得以获取新个体。

第三步：按照轮盘赌机制生成随机数，将其作为模型分析数据支撑。其中，随机数要求与适应度函数值比例保持一致，合理选取数值作为负荷强度个体，转入下一代个体，运用精英保留策略评价这些个体。经过计算分析，得到可靠性预测相关数据，作为评价分析参考依据。

第四步：从客观评价角度出发，对桥面种群进行评价分析。

第五步：按照遗传算法的父子体系结构，先对子代结构中的种群进行评价，将其作为父代评价研究，逐层评价后，得到最终负荷强度可靠性预测结果。

按照上述操作，对桥面负荷强度加以预测，可以得到较为可靠的预测结果。

4 钢结构桥梁桥面负荷强度可靠性预测模型应用分析

为了检测本文提出的预测模型在负荷强度预测中适用性，本文以3 个桥梁建设项目为例，分别对这3 个项目的预测指标进行计算，作为模型预测可靠性评价依据。其中，作为对照的预测模型为文献[4]和文献[5]中的预测模型，预测指标有4 个，分别是均方误差（记为MSE）、相关系数（记为M）、平均绝对百分比误差（记为MAPE）、平均绝对误差（记为MAE）。采用不同预测模型计算相关评价指标，结果如表1 所示。

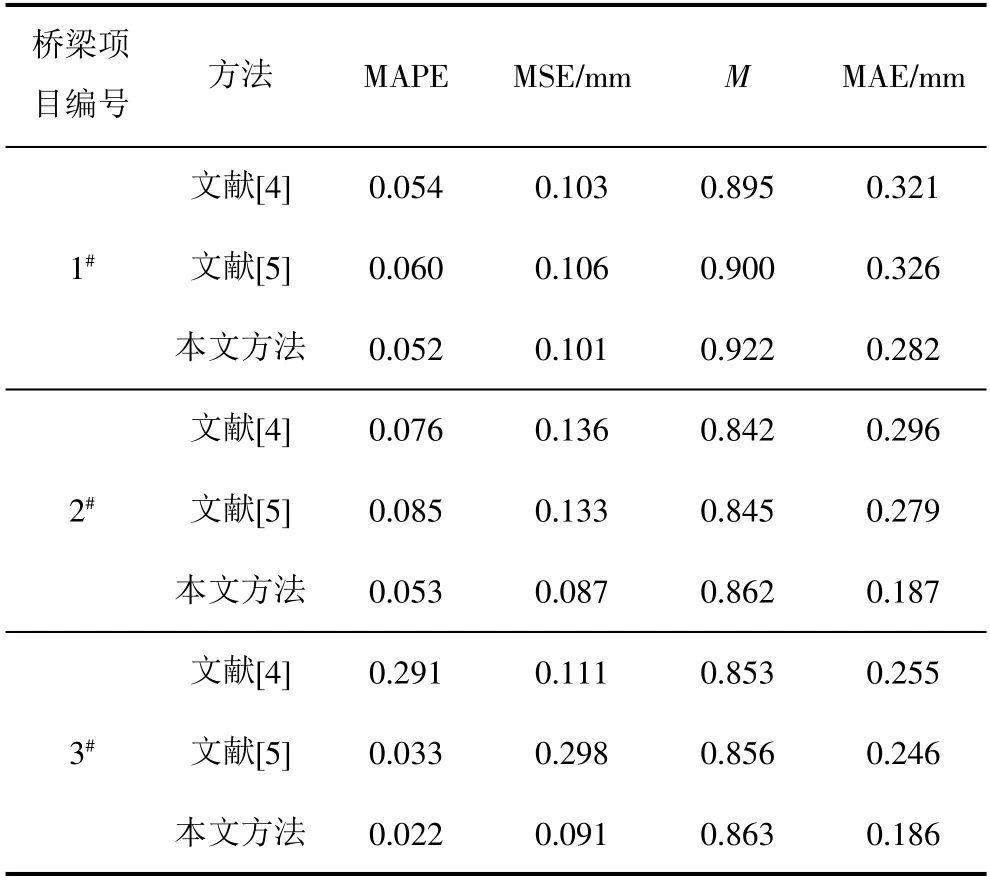
表1 不同预测模型应用下的负荷强度可靠性预测效果评价指标数值统计结果

表1 中统计结果显示，与其他两种预测模型相比，本预测模型的MAPE、MSE、MAE 数值较小，M 数值较大。由此看来，本文设计的预测模型中的系数与实际监测沉降量相关性较大，各项误差数值较小，大大提高了模型的预测结果精准度，使得负荷强度预测结果可靠性较高。按照评估技术指南，预测实验开展中，建议设定各项参数数值为：MAPE=0.08，MAE=0.48 mm，MSE=0.49 mm，M=0.78。

为了更为直观地检验本模型的预测可靠性，以1#项目为例，运用上述参数数值来拟合预测结果，同时也是对本文提出的负荷强度预测模型可靠性进行检验，通过与实际桥面监测沉降量进行对比，得出相应结论。其中，本文模型的预测结果以拟合曲线的形式呈现，结果如图1 所示。

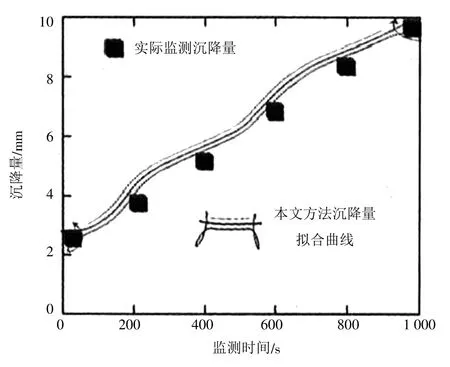
图1 钢结构桥梁桥面负荷强度可靠性预测结果

图1 中本预测模型形成的桥面沉降量拟合曲线与实际监测沉降量数值变化趋势保持一致，并且大部分实际数值与曲线重合。由此看来，本预测模型的拟合度较高，与实际监测数值相差较小，可以作为桥面沉降预测工具，通过预测负荷强度变化规律，从中得出一些可靠性较高的信息。

5 结语

本文围绕钢结构桥梁桥面负荷强度预测方法展开探究，针对以往设计的预测模型存在的不足，引入双曲线算法、遗传算法，展开新的预测模型研究。该模型建立在“三点法”预测模型基础上，通过设定种群，计算种群中的变异概率，对负荷强度加以预测。应用结果显示，与以往预测模型相比，本文提出的预测模型误差较小，拟合度较高，可以作为桥面施工可靠性分析工具。