类旗帜型滞回模型体系的近断层等损伤位移谱

胡进军，刘巴黎，谢礼立

(1. 中国地震局工程力学研究所，哈尔滨 150080；2. 中国地震局地震工程与工程振动重点实验室，哈尔滨 150080)

基于性态的抗震设计理念由于同时考虑地震中结构的安全以及结构的损伤而成为结构抗震设计的热点之一，基于位移的抗震设计是实现基于性态的抗震设计理念最成熟以及应用最广的方法，其中弹塑性位移反应谱的确定最为关键。弹塑性位移谱主要包括等强度的弹塑性位移谱[1-5]以及等延性的弹塑性位移谱[6-9]。等强度的弹塑性位移谱主要应用于既有结构的抗震性能评估，而等延性的弹塑性位移谱主要针对的是新建结构的设计。值得注意的是，等强度和等延性的弹塑性位移谱本质上都仅考虑位移响应对结构破坏的影响，不能同时考虑位移响应和地震动持时或者累积滞回耗能对结构破坏的耦合影响。Park-Ang[10-11]双参数损伤模型能综合考虑结构位移和滞回耗能，近似反映地震作用下结构位移首次超越及累积塑性损伤耦合作用的破坏机理，在结构地震损伤评估方面具有一定的先进性而被广泛采用。

近断层脉冲型地震动由于其复杂的特性以及对工程结构严重的破坏性而广受关注。李宇等[12]系统研究了近场地震动作用下梁式桥的弹塑性反应谱，同时建立了与规范相对应的近场地震动下的弹塑性反应谱。Iervolino 等[13]及Ruiz-García[14]研究了近断层脉冲型地震下等强度位移比谱，结果表明脉冲型地震动的高频分量对短周期段内的位移比谱谱值有放大效应。Wen 等[15]研究了近场脉冲型地震动下双折线弹塑性模型、修正Clough模型以及三线性退化模型的等损伤弹塑性位移谱，结果表明与普通地震动下弹塑性位移谱值相比，近场脉冲型地震动下弹塑性位移谱值在中等周期范围内增幅达到38%。此外，自复位结构因具有延性好、残余位移小及损伤小等特点而成为结构抗震设计的新方向。李爱群等[16]针对旗帜型滞回模型体系，建立了近断层脉冲型地震下滞回模型参数以及延性系数的周期标准化的等延性弹塑性位移谱。武大洋等[17]针对复合自复位结构，研究了近断层脉冲型地震动下该类体系的刚度需求谱。杨博雅等[18]建立了自复位体系等强度延性谱，研究了不同参数对自复位体系延性需求的影响。刘璐等[19]建立了基于自复位结构的改进型等强度位移谱。徐龙河等[20-22]针对钢筋混凝土框架结构、钢框架和斜拉桥，对设置预压弹簧自复位耗能支撑的结构抗震性能进行了研究。De Francesco[23]系统研究了自复位体系的等延性弹塑性位移谱，拓展了弹塑性位移谱的应用范围。Shi 等[24]和Qiu 等[25]研究了形状记忆合金(shape memory alloys, SMA)自复位支撑钢框架的抗震性能，结果表明SMA 能够有效的降低结构地震响应以及减小震后结构残余变形。Zhou 等[26-27]针对单自由度自复位体系分别建立了输入能量谱和滞回耗能谱，研究了延性系数、耗能系数等参数对输入能量谱和滞回耗能谱的影响。目前，自复位体系弹塑性位移反应谱的研究还局限于基于强度和基于延性的方法。鉴于自复位结构耗能强及损伤小的特性，有必要定量研究自复位体系基于损伤的位移谱。

针对上述问题，本文建立了近断层脉冲型地震动作用下自复位体系等损伤位移谱，探讨了类旗帜型滞回模型参数以及损伤指标评价模型参数对等损伤位移谱的影响，对比分析了自复位体系等损伤与等延性位移谱以及近断层脉冲型与无脉冲地震动作用下等损伤位移谱的差异，并通过非线性回归分析建立了近断层脉冲型地震下自复位体系等损伤位移谱预测方程，以期为自复位体系基于性态的抗震设计提供参考。

1 近断层脉冲型地震动

Baker[28]基于小波变换方法从来源于美国太平洋地震工程研究中心(PEER NGA-West2)强震数据库的3500 条地震动记录中识别出91 条垂直断层方向的脉冲型地震动。本文采用这91 条脉冲型地震动同时剔除Joyner-Boore 距离大于30 km 的10 条地震动[29]，基于81 条地震动来研究近断层脉冲型地震动作用下的位移谱。无脉冲地震动记录细分为远场地震动记录和近场无脉冲地震动记录，分别采用FEMA P695[30]建议的22 条远场地震动记录和14 条近场无脉冲地震动记录。部分近断层脉冲型与无脉冲地震动信息如表1 所示。其中，Tp为脉冲型地震动的脉冲周期，采用文献[28]建议的方法，提取小波分析中最大的小波基对应的周期作为脉冲型地震动的脉冲周期。Tg为地震动(脉冲型地震动和无脉冲地震动)速度反应谱峰值对应的周期，即卓越周期。

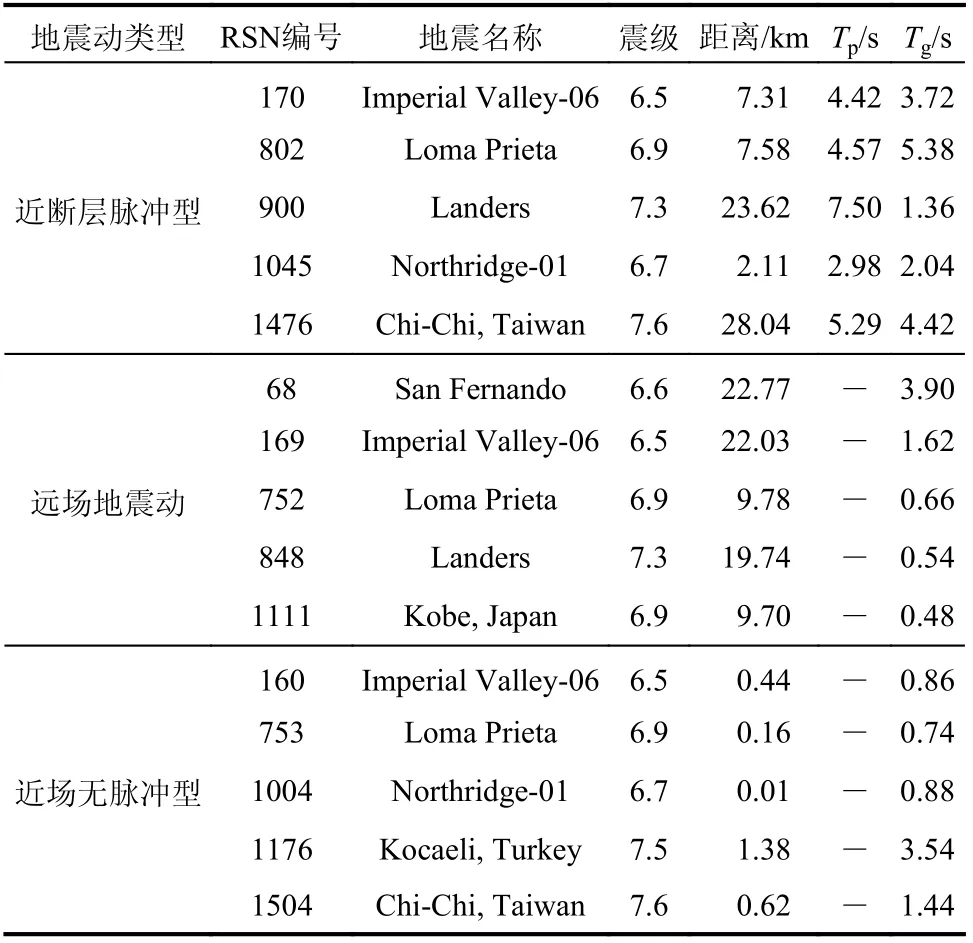
表1 部分近断层脉冲型与无脉冲地震动记录Table 1 List of part near-fault pulse-like records and no pulse-like records

2 等损伤位移谱

2.1 损伤指标评价模型

Park-Ang[10-11]损伤指标可综合考虑结构最大位移响应和累积滞回耗能的影响，被研究人员广泛采用。然而，Park-Ang 损伤模型存在单调加载破坏时损伤指标大于1 以及弹性阶段损伤指标不等于0 等不足。针对Park-Ang 损伤模型中存在的问题，Kunnath 等[31]提出了改进的Park-Ang 损伤指标，能较为精确地反映结构的累积损伤，改进的Park-Ang 损伤指标表达式为：

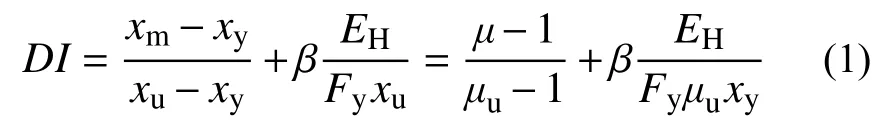
式中：xm为最大位移；xy为屈服位移；xu为极限位移；Fy为屈服力；EH为滞回耗能；μ为延性系数，为xm与xy的比值；μu为极限延性系数，是结构构件在单调加载下的破坏极限位移延性系数；β 为耗能因子，用来衡量循环加载对结构破坏的影响，对于延性差的结构构件β 应该取较大值，反之取较小值。Park 和Ang[10-11]指出不同类型结构具有不同的耗能因子。Cosenza 等[32]基于大量构件的试验分析，研究表明耗能因子具有统计意义上的中位值β = 0.15。Zhai 等[33]分析了耗能因子对等损伤位移谱的影响，研究表明，在短周期段内耗能因子对等损伤位移谱的影响达到28%。Park-Ang 损伤指标及其改进型对极限延性系数的变化较为敏感，结构的极限延性系数往往难以确定。Zhai 等[33]分析了极限延性系数对等损伤位移谱的影响，研究表明在短周期段内极限延性系数对等损伤位移谱的影响超过20%。Wen 等[34]分析了主余震地震下极限延性系数对等强度损伤谱的影响，研究表明在整个周期段内极限延性系数对损伤谱的影响超过70%。

不同损伤状态对应的损伤指标值没有严格的界限。Park 和Ang[10-11]给出了基本完好、轻微破坏、中等破坏、严重破坏及倒塌5 种损伤状态对应的4 个损伤指标限值分别为0.10、0.25、0.40及1.00，欧进萍等[35]给出的5 种损伤状态对应的4 个损伤指标限值分别为0.2、0.4、0.6 及0.9，牛荻涛等[36]给出的5 种损伤状态对应的4 个损伤指标限值分别为0.20、0.40、0.65 及0.90，王东升等[37]建议中等破坏和倒塌损伤状态损伤指数的限值为0.4 和0.8。综合上述研究人员给出的不同损伤状态对应的损伤指标限值，本文按照表2 所示的损伤指标限值对同损伤状态进行划分。

表2 不同损伤状态对应的损伤指标Table 2 Relationship among damage index ranges and degree of damage

2.2 类旗帜型滞回模型

本文采用类旗帜型滞回模型来表征自复位体系的基本特性。耗能系数η 决定类旗帜型滞回模型的滞回特性，其中耗能系数η 为双折线弹塑性模型和旗帜型滞回模型具有相同最大位移条件下的耗能比，取值范围为0～1。当η = 0 时，类旗帜型滞回模型退化为双折线弹性模型；当η = 1 时，类旗帜型滞回模型演化为双折线弹塑性模型。当0＜η＜1 时，类旗帜型模型即为常见的旗帜型模型。此三类滞回模型分别如图1 所示。根据De Francesco[23]的研究结果，取耗能系数η = 0.2 和η = 0.5，分别代表自复位体系较低和较高的耗能能力。屈服后刚度比α 为模型第二刚度与初始刚度的比值。徐龙河等[38]研究自复位耗能支撑时取α 为0.05～0.20，杨博雅等[18]研究自复位体系弹塑性反应谱时取α 为0.00～0.20。值得注意的是，本文所述的类旗帜型滞回模型为理想旗帜型滞回模型，应区别于文献[39]介绍的指向峰值旗帜型滞回模型和刚度退化旗帜型滞回模型。

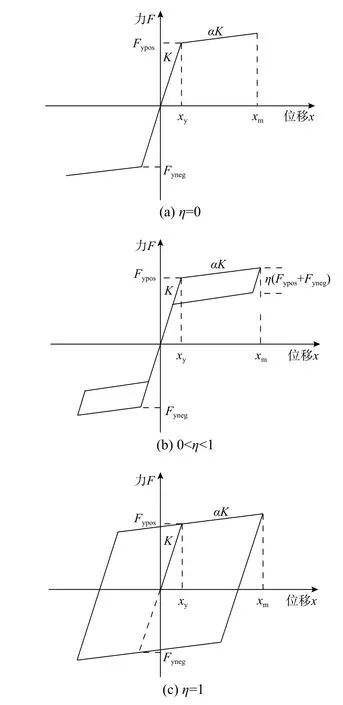
图1 类旗帜型滞回模型Fig. 1 The generalized flag-shaped hysteretic model

2.3 等损伤位移谱理论

单自由度弹性体系和弹塑性体系的运动方程分别如以下：

式中，EI、EK、ED及ES分别为体系的输入能量、动能、阻尼耗能以及弹性变形能。滞回耗能EH可表示为：

基于以上推导，可以建立单自由度体系的位移谱，在此基础上编制了弹塑性时程分析程序，通过时程分析建立等损伤位移谱。弹塑性时程分析程序的运行流程如图2 所示。位移比CDI为自复位体系弹塑性位移xm与具有相同初始刚度的体系弹性位移xe之比，通过求解单自由度弹性体系运动方程可求得弹性位移xe，通过求解单自由度弹塑性体系运动方程可求得弹塑性位移xm及滞回耗能EH。

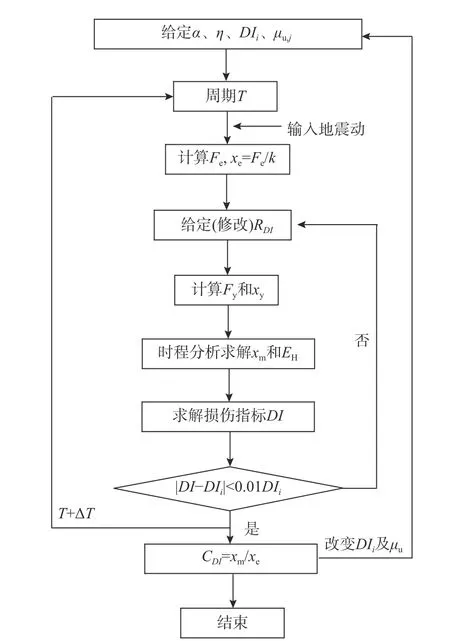
图2 CDI 谱计算流程Fig. 2 Procedure for calculation of constant-damage displacement spectra

2.4 地震动幅值的影响

本文对选取的近断层脉冲型地震动未进行调幅。值得注意的是，杨伟等[40]研究发现，对于给定的损伤指标DI，结构的强度折减系数R(最大弹性力Fe与屈服力Fy之比)不受地震动幅值的影响。刘璐等[41]证明了自复位体系的等强度弹塑性位移谱与地震动幅值无关。同理，对于给定损伤指标DI，自复位体系的CDI谱与地震动幅值无关。为了验证这一结论，以RSN615_WHITTIER地震动作为输入建立了加速度幅值分别为0.2g及2.0g的CDI谱。体系参数：损伤指标DI为0.4，极限延性系数μu为10，耗能因子β 为0.15，屈服后刚度比α 取为0，耗能系数η 为0.2。图3 表明地震动幅值对CDI谱没有影响。

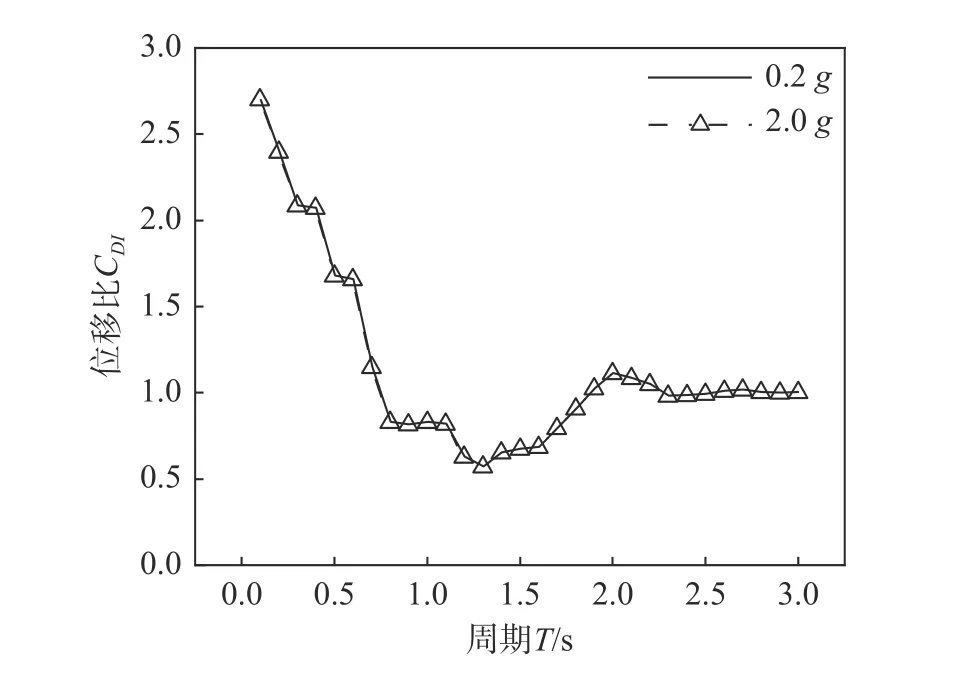
图3 地震动幅值对CDI 谱的影响Fig. 3 Effect of ground motion intensity on constant-damage displacement spectra

2.5 周期标准化

近断层脉冲型地震动和软土场地下的弹塑性反应谱通常采用周期标准化的形式，Iervolino 等[13]、Mavroeidis 等[42]以及Ruiz-García 等[14]研究弹塑性位移反应谱时都采用周期标准化的形式。反应谱的周期标准化，即将自振周期T除以地震动的“特征周期”。常用的周期标准化的“特征周期”主要有脉冲周期Tp和卓越周期Tg。周期标准化的目的主要是为了体现地震动的频谱特性差异对反应谱的影响以及减小反应谱的离散性。图4(a)、图4(b)及图4(c)分别为未进行周期标准化、采用Tg进行周期标准化及采用Tp进行周期标准化的CDI谱，图5(a)、图4(b)及图4(c)分别为对应的变异系数COV 谱。

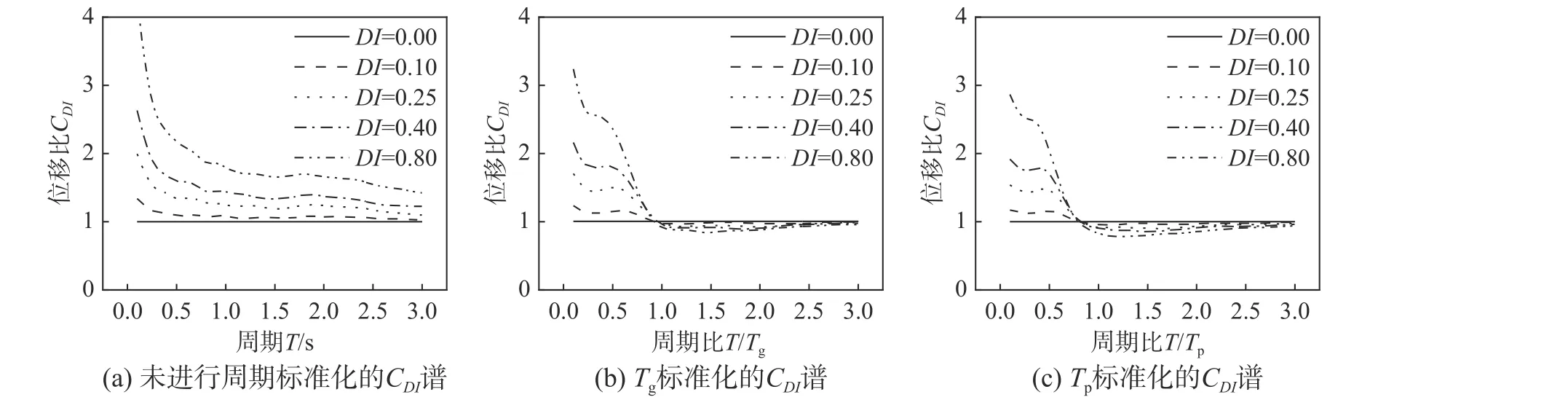
图4 周期标准化对CDI 谱的影响Fig. 4 Effect of period normalization on constant-damage displacement spectra

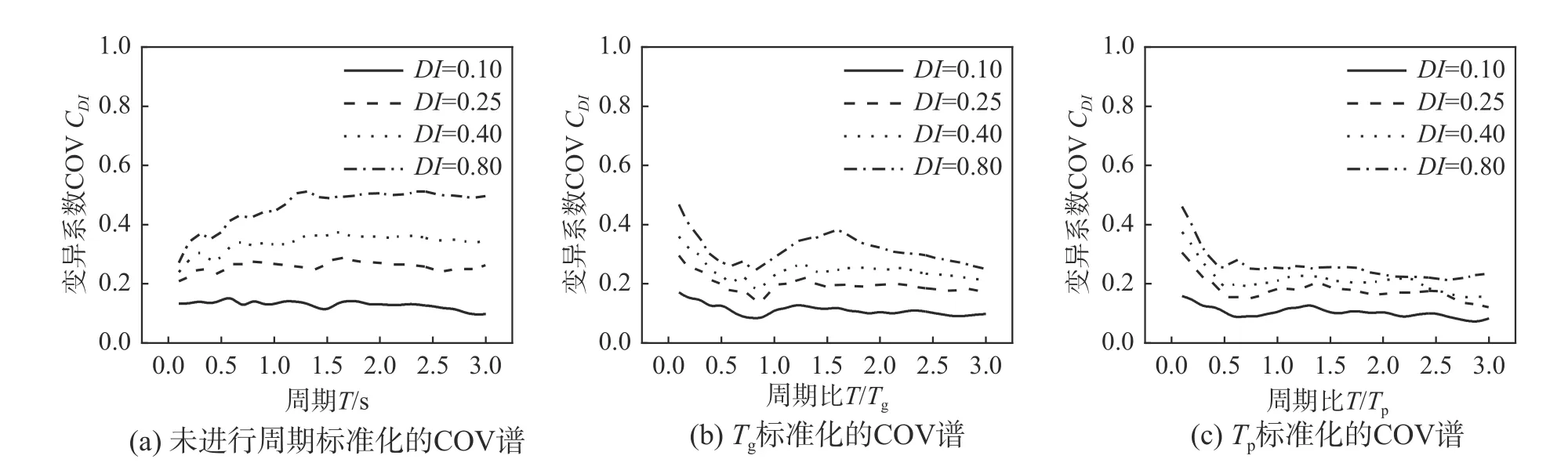
图5 周期标准化对CDI 谱离散性的影响Fig. 5 Effect of period normalization on the coefficient of variation of constant-damage displacement ratios

从平均值的角度分析，采用Tg和Tp进行周期标准化的CDI谱形很相似。不同损伤指标下的CDI谱曲线存在一个交点，CDI谱值在交点周期之前随周期减小以及损伤指标增大而增大。在此周期段内，CDI谱曲线出现“鼓包”，反映了近断层脉冲型地震动高频分量对CDI谱的局部放大效应。CDI谱值在交点周期之后随损伤指标增大有减小的趋势。CDI曲线的交点是弹塑性位移是否大于弹性位移的临界点，同时也是CDI谱是否满足“等位移准则”的临界点。未进行周期标准化的CDI谱值在整个周期段内随损伤指标增大而增大，且CDI谱曲线未出现“鼓包”，不能反映近断层脉冲型地震动对CDI谱的局部放大效应。从离散性的角度分析，除了较短周期段，采用Tg和Tp进行周期标准化CDI谱的离散性都小于未进行周期标准化CDI谱离散性。此外，对于较大损伤指标(DI= 0.8)的CDI谱来说，采用Tp进行周期标准化CDI谱离散性在中长周期段内小于采用Tg进行周期标准化CDI谱离散性。综合而言，采用Tp进行周期标准化来研究CDI谱更为合理，采用Tp进行周期标准化更能反映脉冲型地震动特性，本文后续关于CDI的谱分析均采用Tp进行周期标准化。

3 等损伤位移谱分析

3.1 分析变量

针对具有类旗帜型滞回模型的单自由度体系进行弹塑性时程分析，采用Newmark-β 法求解运动方程，按照2.3 节介绍的计算流程建立CDI谱，积分采用文献[43]建议的步长，即地震动记录采样时间间隔、自振周期的1/25 以及0.01 s 三者的最小值。分析中考虑的变量如下：

1)标准化周期T/Tp取为0.1～3.0，间隔为0.1；

2)损伤指标DI按照表2 取不同损伤状态对应损伤指标的界限值，即DI= 0.10、0.25、0.40 及0.80；

3)损伤模型参数：极限延性系数μu取为6、10及14，耗能因子β 取为0.05、0.15 及0.25；

4)滞回模型参数：耗能系数η 取为0.0、0.5及1.0，屈服后刚度比α 取为0.0、0.1 及0.2。

3.2 损伤指标评价模型的影响

图6 给出了考虑不同损伤模型参数(极限延性系数μu和耗能因子β)相互影响的CDI均值谱。总体而言，不同损伤指标下的CDI谱值随极限延性系数μu增大而增大，随耗能因子β 增大而减小。CDI均值谱大致可分为3 个谱域，CDI谱曲线簇交于一点且交点对应的标准化周期T/Tp为0.8。当T/Tp＜0.8 时，CDI谱值随T/Tp减小以及损伤指标增大而增大，且CDI谱值大于1。此时CDI谱曲线在T/Tp为0.5 左右时出现“鼓包”，反映了近断层脉冲型地震动高频分量对弹塑性位移谱的局部放大效应，脉冲效应容易激发结构的高阶振型；当0.8＜T/Tp＜2.0 时，CDI谱值随损伤指标增大略有减小且其值小于1。CDI谱值在T/Tp接近于1 时取最小值，结构自振周期T与脉冲周期Tp接近时，脉冲型地震动作用下结构进入大量非线性滞回循环，从而导致结构在第一次屈服后由于复位特性而产生较小塑性变形。当T/Tp＞2.0 时，不同损伤指标下的CDI谱值接近于1，此时CDI谱满足“等位移准则”。值得注意的是，当T/Tp＞0.8 时可认为CDI谱近似满足“等位移准则”，此时对结构弹塑性位移的估计趋于保守。

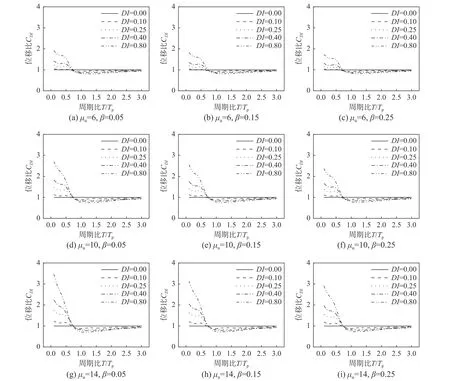
图6 损伤指标评价模型对CDI 谱的影响Fig. 6 Effect of damage model on constant-damage displacement spectra

图7(a)和图7(b)给出了单独考虑极限延性系数μu的CDI均值谱。可以看出：标准化周期T/Tp大于0.8 时，μu为6 和14 对应的CDI谱值与μu为10的CDI谱值之比小于10%，说明在此周期范围内极限延性系数μu对CDI均值谱的影响较小；标准化周期T/Tp小于0.8 时，μu为6 的CDI谱值与μu为10 的CDI谱值之比随损伤指标DI增大而减小，μu为14 的CDI谱值与μu为10 的CDI谱值之比随损伤指标DI增大而增大，μu为6 和14 对应的CDI谱值与μu为10 的CDI谱值之比超过20%，说明在此周期范围内极限延性系数μu对CDI均值谱的影响随损伤指标DI增大而增大。

图7(c)和图7(d)给出了单独考虑耗能因子β 的CDI均值谱。可以看出：在整个周期范围内(除少数几个周期点外)，β 为0.05 和0.25 对应的CDI谱值与β 为0.15 的CDI谱值之比小于5%，说明在整个周期范围内耗能因子β 对CDI均值谱的影响较小。综合而言，对自复位体系设计为有较小延性系数的结构在一定程度上可以减小其位移需求。

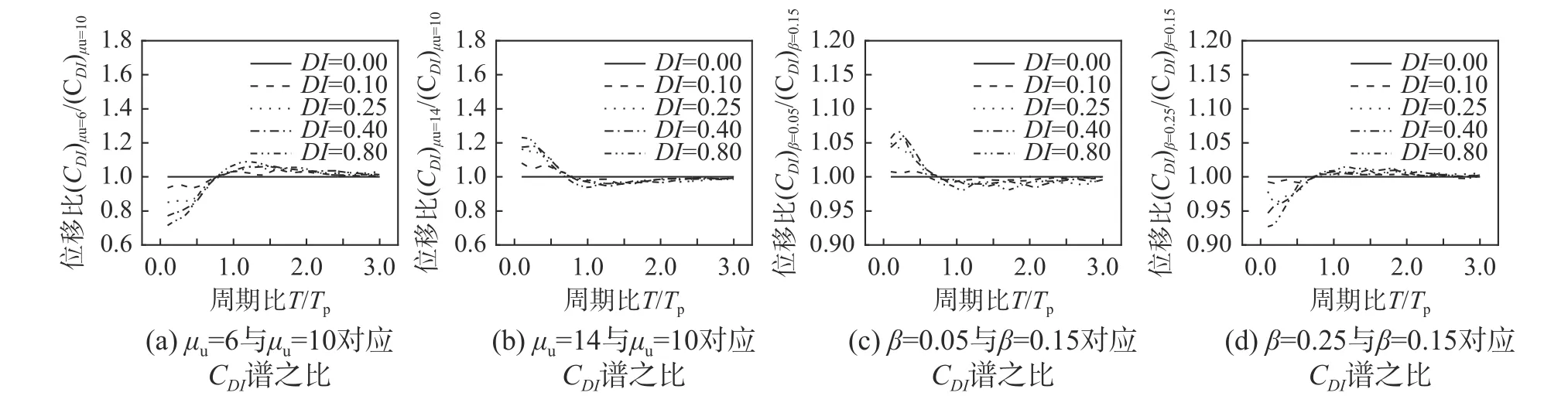
图7 极限延性系数μu 和耗能因子β 对CDI 谱的影响Fig. 7 Effect of ultimate ductility capacity and energy dissipation factor on constant-damage displacement spectra

3.3 滞回模型的影响

图8 给出了考虑不同滞回模型参数(屈服后刚度比α 和耗能系数η)相互影响的CDI均值谱。总体而言，不同滞回模型参数下的CDI谱形与3.2 节不同损伤模型参数下的CDI谱形一致，不同损伤指标下的CDI谱值随屈服后刚度比α 及耗能系数η增大而减小。

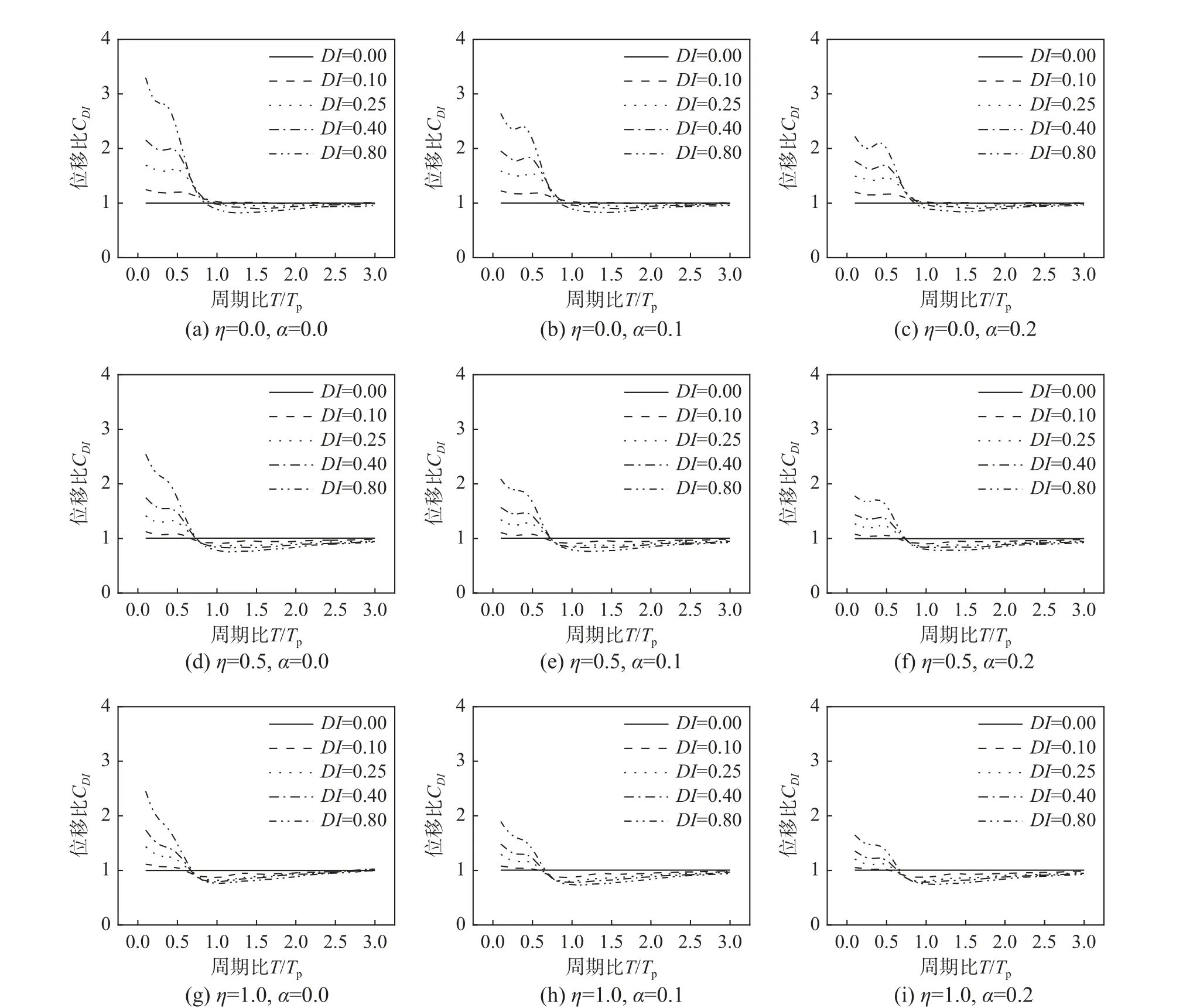
图8 滞回模型对CDI 谱的影响Fig. 8 Effect of hysteretic behavior on constant-damage displacement spectra

图9(a)和图9(b)给出了单独考虑耗能系数η 的CDI均值谱。可以看出：标准化周期T/Tp大于1.0时，不同η 对应的CDI谱差距较小，说明在此周期范围内耗能系数η 对CDI均值谱的影响较小；标准化周期T/Tp小于1.0 时，CDI谱值随η 增大而减小；在整个周期段内，η 为1.0(模型耗能能力强)的CDI谱与η 为0.5(模型耗能能力中等)的CDI谱差距较小，η 为0.0(模型耗能能力差)的CDI谱与η 为0.5(模型耗能能力中等)的CDI谱差距较大，说明自复位体系耗能能力对CDI谱的影响随耗能系数η 增大而变小。

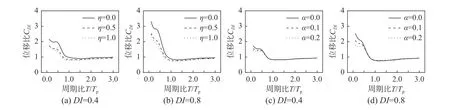
图9 耗能系数η 和屈服后刚度比α 对CDI 谱的影响Fig. 9 Effect of energy dissipation factor and post-yield stiffness ratio on constant-damage displacement spectra

图9(c)和图9(d)给出了单独考虑屈服后刚度比α 的CDI均值谱。可以看出：标准化周期T/Tp大于0.5 时，不同α 对应的CDI谱值几乎相等，说明在此周期范围内屈服后刚度比α 对CDI均值谱的影响可以忽略；标准化周期T/Tp小于0.5 时，CDI谱值随α 增大而减小。综合而言，对于自复位体系，在一定程度上增大屈服后刚度比α 及耗能系数η，可以减小其位移需求。

4 预测模型回归分析

弹塑性谱模型的确定是实现基于位移的抗震设计方法的关键，回归分析的目的是为了建立统一的弹塑性谱模型，以便于结构抗震设计使用。由图6 和图8 可以发现，不同损伤指标的CDI谱具有较为一致的谱形，CDI谱主要受损伤指标DI、极限延性系数μu、耗能系数η 以及屈服后刚度比α 的影响。本文只讨论耗能系数η 为0.5(中等耗能水平)及屈服后刚度比α 为0.0 的自复位体系CDI谱。同时，构造的函数式必需满足式(11)和式(12)所示物理边界条件，其中式(11)确保构造的函数式CDI在中长周期范围内满足“等位移准则”，式(12)确保结构在弹性状态下构造的函数式CDI恒等于1。

式中，a、b、c和d为回归参数。表3 给出了不同极限延性系数μu下的回归参数值以及拟合优度。从图10 中CDI谱统计值与拟合值的对比以及表3中拟合优度可以看出本文构建的CDI谱拟合公式能较为精确地预测自复位体系等损伤位移响应。

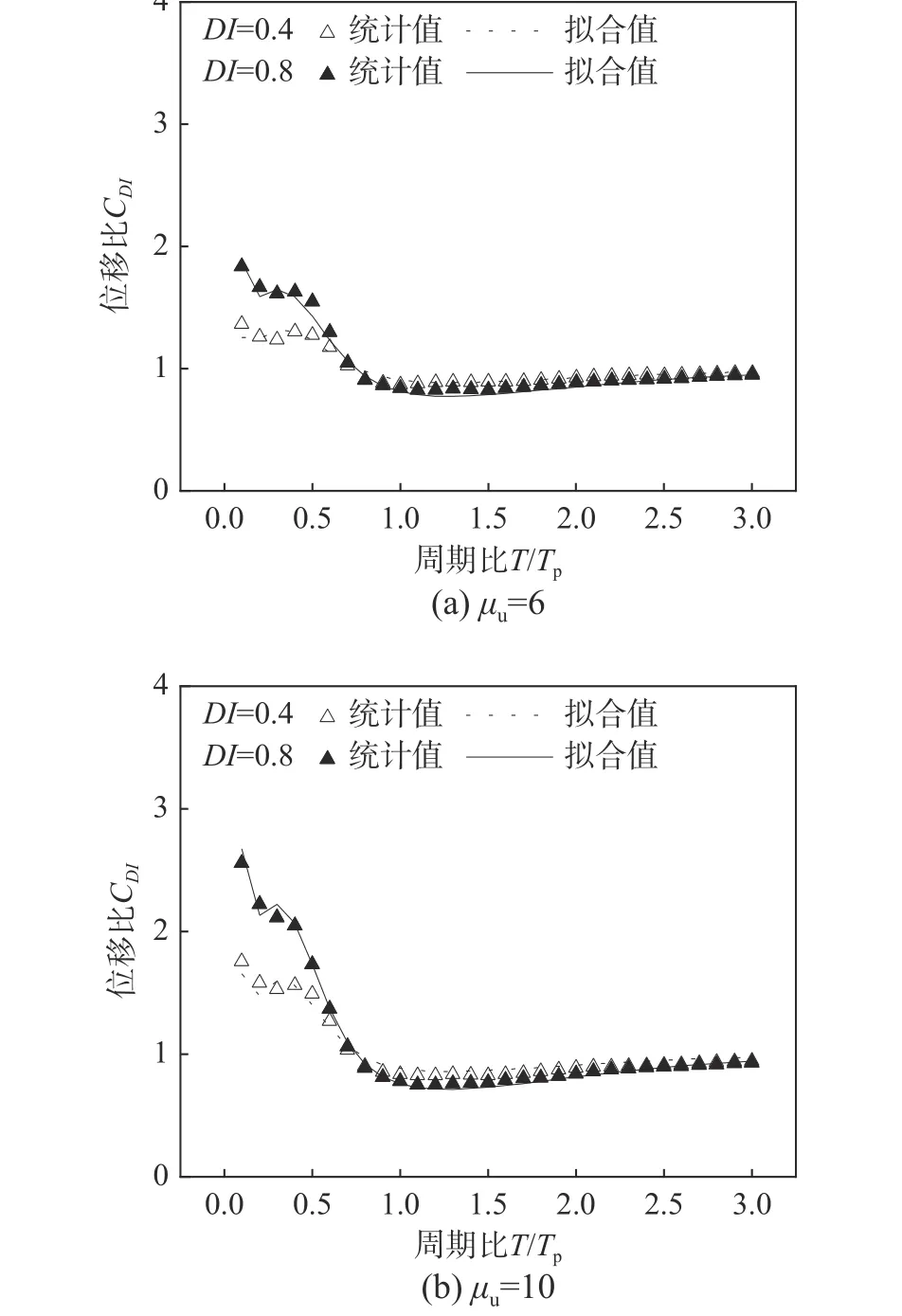
图10 CDI 谱统计值与拟合值对比Fig. 10 Comparisons between statistical results and prediction results of constant-damage displacement spectra

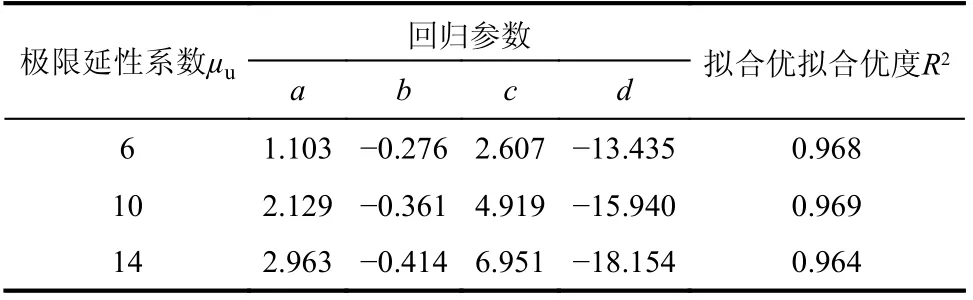
表3 回归参数Table 3 Parameters of regressive formulas

5 CDI 谱与Cμ谱对比分析

基于延性的弹塑性位移谱Cμ仅考虑位移响应对结构破坏的影响，不能同时考虑位移响应和累积滞回耗能对结构破坏的耦合影响。由于结构延性能力通常大于延性需求，则Cμ谱对延性的考虑也不是基于极限状态。这两点是Cμ谱与本文提出的CDI谱的最大区别之处。

图11 给出了μu分别为6、10 及14 对应的Cμ谱与CDI谱之比(损伤指标DI= 0.8)，可以看出：当T/Tp＜0.8 时，不同μu对应的谱比大于1.0，说明CDI谱值小于Cμ谱值；当0.8＜T/Tp＜2.0 时，不同μu对应的谱比小于1.0，此时CDI谱值大于Cμ谱值；当T/Tp＞2.0 时，不同μu对应的CDI谱值与Cμ谱值差距较小，此时CDI谱与Cμ谱均近似满足“等位移准则”。总体而言，累积滞回耗能对自复位体系位移需求的影响不能忽视。在短周期段(T/Tp＜0.8)内，与基于损伤理论相比，基于延性理论的结构弹塑性位移估计趋于保守；在中长周期段(0.8＜T/Tp＜2.0)内，与基于损伤理论相比，基于延性理论的结构弹塑性位移估计趋于不保守；在长周期段(T/Tp＞2.0)内，基于损伤理论和基于延性理论的位移谱均满足“等位移准则”。

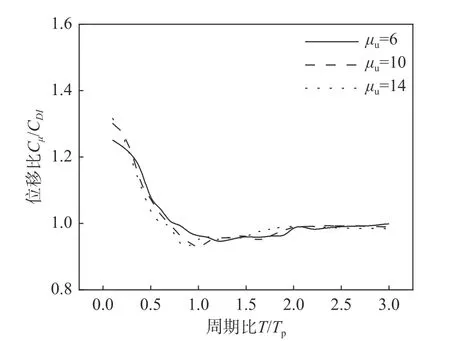
图11 CDI 谱和Cμ谱对比分析Fig. 11 Comparisons between constant-damage displacement spectra and constant-ductility displacement spectra

6 近断层脉冲型地震动CDI 谱与无脉冲地震动CDI 谱对比分析

图12 给出了近断层脉冲型地震动下CDI谱与无脉冲地震动下CDI谱之比。其中无脉冲地震动细分为远场地震动和近场无脉冲地震动。由于无脉冲地震动不存在明显的脉冲周期Tp，为了统一指标，此处横坐标采用了T/Tg。对比图12(a)和图12(b)可以发现，近断层脉冲型地震动下与近场无脉冲地震动下CDI谱比和近断层脉冲型地震动下与远场地震动下CDI谱比差别较小。

由图12 可知：T/Tg为0.5 左右时CDI谱比出现第一个峰值，反映了相较于无脉冲地震动，近断层脉冲型地震动高频分量对CDI谱存在局部放大效应。T/Tg为1.0 左右时，CDI谱比出现第二个峰值，其主要原因是：与近断层脉冲型地震动相比，无脉冲地震动有较小的峰值速度PGV 与峰值加速度PGA 比值，即PGV/PGA 值；而地震动卓越周期Tg与PGV/PGA 值正相关，此时无脉冲地震动有较小的Tg；当标准化周期T/Tg为1.0 左右时，脉冲型地震动对应的结构周期T大于无脉冲地震动对应的结构周期T，即相比于近断层脉冲型地震动CDI谱，无脉冲地震动CDI谱有右移的趋势，则近断层脉冲型地震动对应的结构刚度k小于无脉冲地震动对应的结构刚度k，所以结构在脉冲型地震动作用下将经历比无脉冲地震动下更大的位移。此外，T/Tg大于0.5 时CDI谱比相继出现峰值和谷值。此类现象的出现也与无脉冲地震动下结构CDI谱的右移趋势有关。总体而言，与无脉冲地震动CDI谱值相比，近断层脉冲型地震动CDI谱值在T/Tg为0.5 和1.0 时增大20%左右。

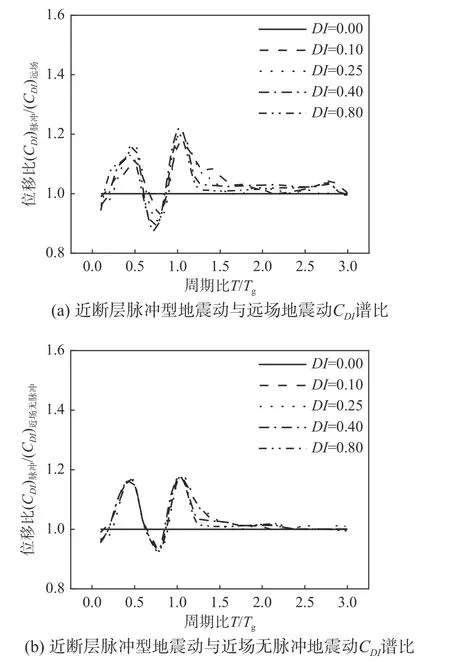
图12 近断层脉冲型地震动CDI 谱和无脉冲型地震动CDI 对比分析Fig. 12 Comparisons between constant-damage displacement spectra subjected to near-fault pulse-like ground motions and no pulse-like ground motions

7 结论

本文研究近断层脉冲型地震动作用下自复位体系的等损伤位移谱，探讨了损伤指标评价模型参数以及类旗帜型滞回模型参数对等损伤位移谱的影响，得出以下主要结论：

(1) 采用脉冲周期Tp进行标准化能够反映脉冲效应对短周期段内等损伤位移谱的局部放大作用，同时能降低等损伤位移谱在中长周期段内的离散性。

(2) 标准化周期T/Tp为0.5 左右时等损伤位移谱出现“鼓包”，反映了近断层脉冲效应对位移谱的局部放大作用；T/Tp为1 左右时等损伤位移谱值最小，此时结构自振周期T与脉冲周期Tp接近，结构进入大量非线性滞回循环后由于复位特性而产生较小塑性变形；T/Tp大于2.0 时，等损伤位移谱值接近于1，此时等损伤位移谱满足“等位移准则”。

(3) 在整个周期范围内，耗能因子β 对等损伤位移谱的影响不超过5%；标准化周期T/Tp小于0.8 时，极限延性系数μu对等损伤位移谱的影响超过20%。

(4) 标准化周期T/Tp大于0.5 时，屈服后刚度比对自复位体系等损伤位移谱的影响不明显，在此周期段内研究自复位体系等损伤位移谱时可以忽略屈服后刚度比的影响；在整个周期段内，自复位体系耗能能力对等损伤位移谱的影响随耗能系数η 增大而变小；在一定程度上增大屈服后刚度比α 或耗能系数η，可以减小自复位体系位移需求。

(5) 基于延性的位移谱与基于损伤的位移谱的对比分析，说明累积滞回耗能对自复位体系位移需求的影响不能忽视。与无脉冲地震动位移谱值相比，近断层脉冲型地震动位移谱值在标准化周期T/Tg为0.5 和1.0 时增大20%左右。通过回归分析建立了等损伤位移谱预测模型，结果可用于近断层区域自复位体系位移响应的预测。