多个地震台网相互融合测定震级的贝叶斯算法
2022-06-02司政亚庄建仓蒋长胜
司政亚, 庄建仓, 蒋长胜
1 中国地震局地球物理研究所, 北京 100081 2 北京市地震局, 北京 100080 3 日本统计数理研究所,东京 106-8569
0 引言
地震参数尤其是震级测定结果的一致性,是地震减灾和地球科学研究的重要基础,例如在非常规能源开采诱发地震监测中,当临时布设的流动地震台网测定的地方震震级ML作为风险管控系统的决策参量时,必须对震级测定公式进行校正以使得其与区域地震台网测定结果相一致(Edwards and Douglas, 2014; Mahani and Kao, 2020).近年来在以科学研究为目的临时布设的流动观测地震台网大量出现,例如美国圣安德烈斯断层带上的井下“高精度地震台网”(HRSN, Hickman et al., 2004)、德国/捷克边境布设的小孔径地震阵列(Hiemer et al., 2012)、美国加州长滩密集台阵(Lin et al., 2013)等.大地震发生后快速增设流动地震台网以弥补余震区监测能力不足,也是多数国家地震减灾机构的常规行动.由于流动观测地震台网的台站台基响应、人工拾取震相等数据处理方式与区域地震台网存在差异,且往往位于固定地震台站较为稀疏的地区,或位于地震记录匮乏的弱震区,难于事先进行震级测定的规范校准,给履行监测任务和服务科学研究带来极大困难(刘瑞丰等, 2005, 2006; Scordilis, 2006; Pechmann et al., 2007; Yadav et al., 2012; Anbazhagan and Balakumar, 2019).随着高密度流动测震台网的增多,用便捷可靠的方式获得高一致性的震级测定结果,实现流动观测地震台网与本地固定地震台网真正意义上的融合,成为一项重要的技术挑战.
观测区域重叠或部分重叠的地震台网,常采用3种方式处理共同记录的地震事件:第一种是对不同台网重复记录的地震事件直接删除,实现台网的相互融合,如Viveros等(2017)对跨墨西哥火山带的地震危险性的研究中,直接删除不同研究机构产出数据中重复的地震记录;Wollin等(2018)对马尔马拉地区多个地震台网地震目录的合并中,对发震时刻间隔小于30 s的记录对也直接删除.第二种则采用相同记录的简单合并,不考虑数据融合后的震级差异性问题,如Smith等(2004)基于日本气象厅(JMA)和日本大学台网地震目录(JUNEC)合并后的数据集对板内地震活动性的研究;Piccinini等(2009)基于意大利地区多个固定台网及临时观测台网合并后的数据,进行区域地震构造背景研究;Wetie等(2019)使用不同来源收集的地震目录评估喀麦隆火山区地震危险性问题;以及龙锋等(2018)针对中国不同区域独立运行的地震台网开展地震目录的合并工作.第三种则直接对不同台网产出的地震波形进行合并,重新进行地震定位及震级测定,但忽略不同台网的差异性问题,如Gök等(2009)合并不同台网的波形,研究震源参数的不同估计方法的差异性.前两种对地震目录参数融合问题的处理,本质上是消除其重叠部分数据的差异性,而非融合.通过合并不同台网的地震波形,重新计算地震参数虽然可实现真正的台网融合,但由于其波形获取、计算复杂性等,实际操作中往往十分困难.
为得到多个地震台网融合下科学、一致的地震目录,前人已开展多种尝试.例如,Wang等(2009)在整合加利福尼亚州的多个现有地震目录时,先基于事件的震级误差、震中位置误差为每个目录建立一个优先级列表(相对误差最小的优先级最高),然后将优先级最高的目录为首选,解决了将这些地震数据合并到一个目录中的问题.在震级误差的比较中,Wang等(2009)假定目录是独立的,目录之间的震级差异的方差等于这些目录的震级方差之和.Hiemer等(2012)在小孔径地震台阵的震级测定中,采用与本地固定地震台网相同的震级标度计算公式,基于地震台阵与固定台网震级数据的正交分析,得出二者的线性差异,将此差异常数叠加至震级计算公式中的台站校正项,以此达到了两种台网震级计算的统一.Rezaeifar和Kissling(2018)针对伊朗地区两个观测台网震级测定的差异性,以两个台网对所有共同记录事件的平均震级差为校正项,进而消除两个台网的震级差异.
不同类型台网的观测环境差异可能很大,会对震级测定带来差异性影响.目前对于多个地震台网融合的实际算法中,并未考虑本地固定地震台网与流动观测地震台网之间的震级差异性.Hiemer等(2012)虽考虑了测定震级差异性问题,但所用方法仅适用于采用相同的震级标度计算公式及规则相同,且不考虑不同台网震级测定误差的差异,普适性较低.为此,针对固定地震台网与流动观测地震台网的震级测定差异性问题,本文利用固定台网测定震级优于流动台网的特征,以不同台网的震级标准差为权重,结合震级偏差的概率密度函数,推导得出了基于贝叶斯原理的多地震台网融合下的震级矫正算法.该算法不仅适用于现有地震目录的震级矫正,当数据量足够大时,基于现有数据计算得到的矫正参数,还可直接对未来发生的地震事件进行震级矫正,为研究地震的时空发震模式以及包括地震危险性评估、峰值地面加速度估算、长期地震应变率确定等许多工程应用提供基础数据支持.
1 固定台网与西昌流动台阵标定的震级差异
西昌流动台阵为本文的流动台网研究提供了数据支持.西昌流动台阵是中国地震局地球物理研究所在石棉—冕宁—西昌一带布设的高密度流动观测地震台阵,观测点整体呈南北向分布,南北向展布约220 km,东西向近100 km.此流动台阵由32个宽频带地震台站组成,平均台间距16 km,在石棉地区,平均台间距小于10 km.在2013-01-13—2019-02-01期间,西昌流动观测台阵共计记录地震事件9336个,其中最小地震事件震级为ML-1.4,最大事件为ML4.7.本文计算中所用的地震事件资料及地震观测目录由“中国地震科学台阵数据中心”提供.
“十五期间”,通过实施“中国数字地震观测网络项目”,中国地震局建成了覆盖全国的地震监测台网,建设了统一的地震编目体系(刘瑞丰等, 2015).统一编目由国家测震台网中心,对省级测震台网中心和国家测震台网中心产出的观测报告进行综合处理,生成统一的地震目录和观测报告.国家测震台网中心编目人员下载全部国家台站报送的震相数据,通过震相组合、地震定位、震级测定,产出国家台网地震目录和观测报告,在一周后将结果统一汇入编目数据库,生成中国测震台网(以下简称固定台)统一正式的地震目录和观测报告(代光辉等, 2019).本文所使用的固定台网地震事件资料为中国地震台网中心“全国地震编目系统”提供的《全国统一正式编目》统一正式目录和地震观测报告,筛选时间范围为2013-01-01至2019-02-01,在此期间全国固定台网共记录到地震事件616572个.
为了对比西昌流动台阵和全国固定台网的记录差异,将西昌流动台阵(以下简称流动台网)记录到的地震与固定台网记录到的地震进行匹配,得到两个台网对同一个事件的地震记录,称为一个记录对.对于记录对的识别方式,通常基于这些地震是否在震中位置、发震时刻上局限于某一特定范围,该范围的选定基于一定的经验性.如,Solarino等(1997)在合并阿尔卑斯山区域附近的相邻台网地震数据时,采用发震时刻15 s内与震中距差异40 km内作为相同事件的判定标准.Wang等(2009)在整合加利福尼亚州不同的地震目录时,判别记录对的标准是时空阈值局限在16 s、100 km.龙锋等(2018)在对中国不同区域台网进行数据融合时,选用时空强阈值为5 s、20 km、0.5级.Rezaeifar和Kissling(2018)对伊朗的两个国家观测台网进行数据整合时,采用发震时刻之差小于60 s,各震中之间的距离小于100 km作为相同事件的判别标准.Abbasi(2019)对伊朗地区不同区域台网记录对的识别主要基于发震时刻小于1 s.由于本研究中研究区域较小(南北范围不超过200 km)、区域内流动观测台阵本身布设较密(台间距小于10 km),且固定台网和流动台网各自产出数据质量较高,因此本文中判断两个台网记录的地震为同一个地震的标准更为严格,即两者测定的发震时刻差小于2 s,震中位置的经度及纬度相差小于0.04°.固定台网与西昌流动台网匹配的记录对位置及震级差异情况如图1所示,记录对的数量为2336组.

图1 固定地震台网和流动地震台网匹配的记录对的位置和震级差异情况图(a)(b)(c)分别表示记录对的经度差异、纬度差异及震级差异,其中蓝色的点代表固定地震台网记录的地震事件信息,红色的点代表西昌流动地震台网记录的地震事件信息,图(c)中绿色的线为记录对的连线.图(d)(e)(f)分别为记录对的经度、纬度、震级不同差异情况的频次统计.Fig.1 Differences in the locations and the magnitudes for each matched pairs between the permanent (CN) and the temporary (XC) seismic networksFig.(a) to (c), respectively, show their differences in longitudes, latitudes, and magnitudes. The blue dots represent the events recorded by CN seismic network and the red dots represent the events recorded by XC seismic network. In (c), the green line segments connect each record pair. Fig.(d) to (f) are histograms of the differences corresponding to (a) to (c), respectively.
图2给出了固定台网和流动台网所测定震级之间的关系.从图2上可以看出,固定台网与流动台网记录到的震级整体上呈正相关.从记录对的分布情况上看,震级在0.8~2.0之间,可能存在一个拟合的拐点,拐点两侧的记录对有各自独立的拟合方式.为得到更好的拟合方式,寻找拟合的拐点,采用统计地震学中常用的赤池信息准则(Akaike information criterion),简称AIC准则.具体做法为,将数据分为两个部分,分别做最小二乘拟合,之后计算数据整体的AIC值,AIC值最小时,代表拟合的结果最好.线性拟合情况下的AIC值计算可以表示为(Sakamoto et al., 1986):
AIC(m)=nlog2π+nlogd(m)+n+2(m+2),
(1)
(2)
其中m表示拟合的阶数.在这里,我们认为拐点两侧的记录对满足一阶线性拟合,因此取m=1.
对数据拟合的AIC值分析的结果表明,对全部数据进行最小二乘拟合所得到的AIC值(341.06)大小与通过划分拐点分别拟合所得到的AIC值(339~347)基本一致.随着震级拐点的变化,在震级拐点两侧采用不同的线性拟合方式所得到的AIC值,虽然存在极小值(339.56),但是相对于AIC值本身,变化很小,可以忽略.由此可得,通过一阶线性拟合可以合理的描述固定台网与流动台网所测定的震级差异规律.
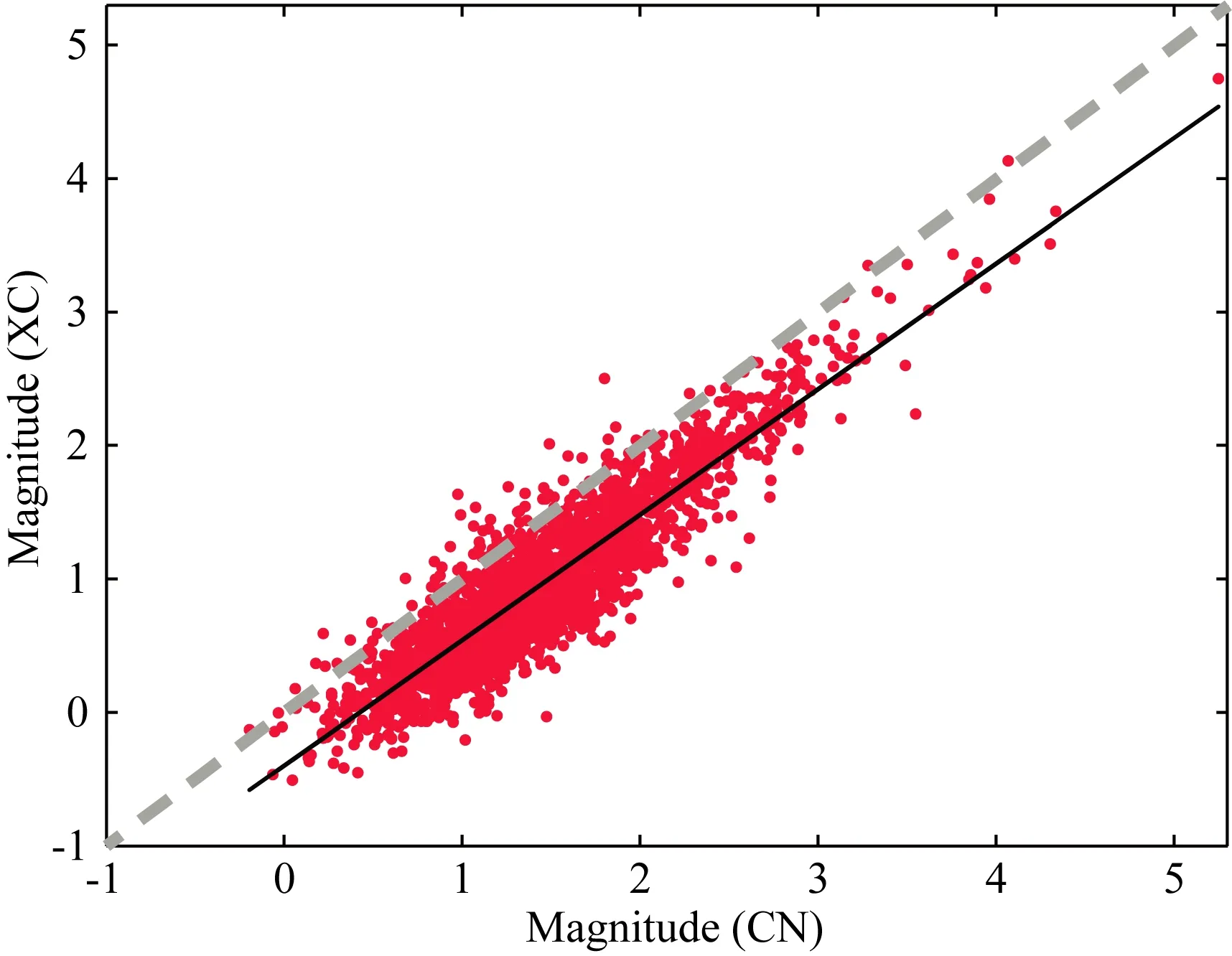
图2 固定地震台网和流动地震台网记录的记录对的震级比较图中浅色虚线为两个地震台网测量的震级相等时的位置,黑色实线为线性回归拟合结果.Fig.2 Magnitude comparison of the each matched pair between permanent and temporary seismic networksThe light dotted line shows the position when the magnitudes measured by the two seismic networks are equal. The black solid line shows the linear regression line.
2 基于统计学方法的震级矫正算法
无论是固定台网还是流动台网,台网本身对于地震震级的测定存在误差,且不同的地震台网震级误差不同.对于同一个地震事件,地震台网中记录到该事件的台站所测定的地震震级往往存在差异.为了较客观的反映地震能量的大小,通常将台网中所有记录到该地震的台站所测定的震级做平均,将得到的平均震级定为地震事件的震级,地震台网会同时给出地震震级所对应的标准差,即震级测定的误差.对于同一个地震台网,所使用的震级计算公式、量规函数及仪器类型通常是相同的,我们可以认为台网所给的震级误差包含了人工测定误差以及因台基状态不同导致的误差.由于震级误差直接影响了台网所测定震级的可靠性,综合固定台网和流动台网的地震记录得到真实地震震级大小时,须同时考虑震级大小和震级误差的差异,按照震级误差的大小对不同台网记录的地震合理分配权重,以此得到综合多种台网的震级记录下的真实震级.
2.1 固定地震台网与一个流动地震台网联合矫正震级
通过对西昌流动地震台网与全国固定台网测定的震级差异分析表明,两者所测定的震级大小存在线性关系,由此可以将流动地震台网与固定地震台网的震级及震级误差通过线性拟合建立联系,构建出新的震级分布关系,真实震级的大小及误差由固定台网和流动台网给定的震级和误差决定.

(3)

(4)
根据贝叶斯公式,在给定固定台网的测定震级m1与流动台网的测定震级m2的条件下,真实震级m的概率密度函数为



(5)


由于固定台网和流动台网的震级记录在给定真实震级m的条件下是相互独立的,即
f2|·1(m2|m,m1)=f2|·(m2|m).
(6)
根据全概率公式,给定固定台网震级m1条件下流动台网震级m2的条件概率密度函数为
(7)
将(6)和(7)式代入(5)式,则
显而易见,(8)式中的分布是一个正态分布,设其均值为μ,标准差为σ2,即
(9)
(10)
附录A给出了该式的详细推导过程.
而给定m1时m2的条件概率密度函数为
(11)
2.2 固定台网与多个流动地震台网联合矫正震级
(10)式可以推广到存在k个不同的台网记录的情形,设各个台网测定的某地震分别为(m1,m2,…,mk)时,其中m1是固定台网记录到的震级,而其他为流动台网记录的,则给定所有观测的情况下,真实震级服从的条件分布为
(12)

(13)
的正态分布.附录B给出了一个简略证明.
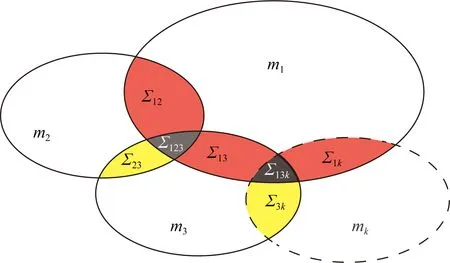
图3 存在多个地震监测台网时,矫正震级计算的数据选择关系椭圆形分别表示固定地震台网记录到的地震事件测定震级m1、流动地震台网记录到的地震事件测定震级m2,m3,…,mk.图中红色、黄色、深灰色区域代表同时被两个或三个地震台网所记录到的地震事件.Fig.3 Illustration of the relationship of data inclusion and exclusion when the records are recorded by multiple monitoring networksEllipse m1 represents the magnitudes recorded by the permanent seismic network, and ellipses m2,m3,…,mk represent magnitude recorded by different temporary seismic networks. The red, yellow, and dark gray areas represent the earthquake events are simultaneously recorded by two or three networks.
当地震事件被多个地震台网同时记录时,结合(12)式的结果,可以得到多个台网加权平均下得到的矫正震级.不同台网之间对于记录的地震事件存在交叉关系,但均可通过(12)式得到地震记录的矫正震级.如图3所示,红色区域Σ12、Σ13、Σ1k代表同时被固定台网及流动台网所记录到的地震事件,黄色区域Σ23、Σ3k代表同时被两个流动台网所记录到的地震事件,深灰色区域Σ123、Σ13k代表同时被固定台网及其他多个流动台网同时记录到的地震事件,这些被多个台网共同记录到的地震事件均可通过(12)式得到相应的矫正震级.实际工作中的地震记录交叉关系会比图3中所示复杂得多,但我们只需确定该地震事件被哪些台网所记录到,即落在图3中的哪个区域,结合(12)式,带入矫正参数,即可快速得到该地震事件所对应的矫正震级.对于被某些台网所单独记录到的地震事件,即图3中的白色区域,由台网与真实震级之间的关系(见(3)式和(4)式),带入矫正参数即可得到真实震级的大小.
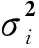
给定k个不同的台网对N个地震的测定结果:
其中缺失数据记为NA.此情况下的观测数据的联合概率密度函数,也就是似然函数为
(14)
而



(15)
式中,我们约定对所有的概率密度函数当NA出现在自变量中,其值为1,即f…(NA|…)=f…(…|NA)=1.
由k个不同的流动台网确定的“观测震级”其最大似然函数为:


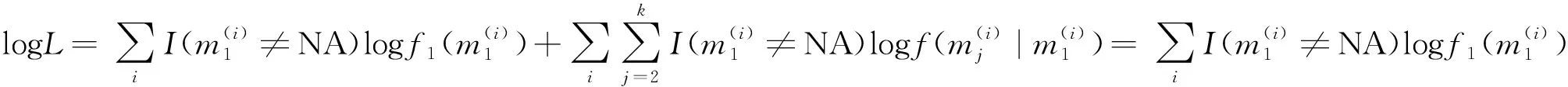
(16)


其中I(A)为逻辑函数,当论断A为真时取值1,否则取值0.
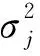

(17)
将这些估计值代入(12)及(13)式就可以分别得到真实震级的估计值(矫正震级)和标准差.
2.4 计算步骤和实现方式
应用到实际的算法上,主要分为两个步骤:

2)按照(12)式的结果,得到由k个台网所确定的矫正震级:
(18)

2.5 数据分析
将算法应用于西昌地区实际地震目录中,得到的结果如图4所示.西昌流动台网与固定台网融合后的矫正震级对两个台网的初始测定震级均存在一定的震级矫正量,矫正震级对固定台网初始测定震级的震级矫正量在M-0.3~M+0.3之间,其频次的分布形态大体呈标准正态分布.矫正震级与西昌流动台网的初始测定震级的震级矫正量范围则在M-0.3~M+1.2之间,震级矫正量集中趋近于M+0.5,离散程度相对较高.从两个台网的震级矫正量频次分布结果中可以看出,我们所发展的多台网震级矫正算法不仅仅是对流动台网的矫正,而是多台网融合后整体矫正.与此同时我们也得到了矫正震级计算所需的矫正参数(表1).矫正参数的值确定之后,结合流动台网与真实震级之间的关系(4),即可将流动台网所测定的地震震级矫正为真实的地震震级.同时,当流动台网的数据量足够多时,可认为其与固定台网所共同确定的矫正参数是稳定的,对于还未发生的地震来说,当地震发生时,通过矫正参数表及震级矫正公式(18)即可快速的对测定震级进行矫正,为地震活动参数的计算提供准确的震级参数.

表1 矫正参数的估计值Table 1 Estimates of correction parameters
3 讨论
不同地震台网共同记录的地震事件测定震级出现差异的本质原因,一方面,对在特定周期测量最大振幅的地方震震级ML和面波震级MS,受制于“单色”和“经典”意义上的震级定义本身,难于应对不同台网之间在传播路径、场地响应和介质衰减上的系统性差异(Mahani and Kao, 2020).另一方面即使对于矩震级MW和能量震级Me等“现代”意义上的震级测定,也难于将地震观测谱中相互耦合的传播路径、场地响应和介质衰减项精准地扣除(Trugman and Shearer, 2017; Picozzi et al., 2017),获得真实的震源谱.这些在物理上难于事先“校正”的震级测定难点,则为统计地震学上的后验的“矫正”提供了发挥空间.

图4 基于贝叶斯算法获得的矫正震级与初始测定震级的比较(a) 表示固定地震台网(蓝色的点)及流动地震台网(红色的点)初始测定震级(横轴)与矫正震级(纵轴)的对比; (b) 表示矫正震级与流动地震台网初始测定震级不同震级差的频次统计; (c) 表示矫正震级与固定地震台网初始测定震级不同震级差的频次统计.Fig.4 Comparison between the revised magnitudes that are calculated by the Bayesian algorithm and the original recorded magnitudes(a) shows a comparison between the revised magnitudes that are calculated by the Bayesian algorithm and the original recorded magnitudes by the CN (blue dots) and XC (red dots) seismic networks. (b) and (c) show histograms of the differences between the revised magnitudes and the original recorded magnitudes by the XC and the CN seismic networks, respectively.
本文提出的基于贝叶斯公式的震级矫正算法的应用不仅仅局限于流动台网的假设,实际上也可应用于如下三种情景:(1)针对固定地震台网测定震级存在缺陷、需要专门布设的流动地震台网进行标定震级的情况.这是由于稀疏分布的本地固定地震台网缺少发生在较浅深度、较近震中距离的地震数据记录,构建的震级测量公式难于获得这些地震事件的准确的震级测定结果(Ottemöller and Sargeant, 2013; Luckett et al., 2019).(2)增加布设的流动地震台网通过地方震震级(ML)与矩震级(MW)的统计分析矫正震级测定公式后,同样可利用本文的方法对固定地震台网的震级结果进行矫正,以及两者的联合矫正,这对水力压裂诱发地震和采矿诱发地震的震级测定具有重要的现实意义(Clarke et al., 2014; Butcher et al., 2017).(3)对于大地震余震区在震后快速布设的流动观测台网,未经过校准的流动观测台站数量远多于本地固定地震台站、记录的大量余震事件的震级几乎全部无法保证可靠性.而利用本文的算法,可将每个流动观测台站均作为等待矫正的“台网”、转变为多台网共同矫正的方式来获得更为可靠的震级测定结果.
对于震级矫正参数,利用本文新发展的算法以及先期计算得到的震级矫正参数,可对流动地震台网未来新发生地震进行快速的震级矫正,得到更为精确的真实震级估计值.震级矫正参数的稳定性将直接影响震级矫正的准确性,而流动地震台网与固定地震台网的布设区域、布设时间、最小完整性震级等的差异,为震级矫正参数稳定性的提高造成一定的阻碍.但当同一研究区域布设有多个流动地震台网时,采用多网融合下的震级矫正算法可有效解决这一问题.多网融合的震级矫正算法有助于显著提升震级矫正结果的稳定性,方法本身具有普适性和更高的应用潜力.
需注意的是,本文发展的基于贝叶斯公式的震级矫正算法,当固定台网的测定震级与事件的真实震级之间的误差并无特定规律、或流动台网测定震级与真实震级之间误差不满足线性分布时,本文所发展的震级融合算法将不适用,仅适用于震级测定的标准差已知的情况,如果需分析的数据不包含震级测定的标准差,则须发展新的算法.Castellaro等(2006)认为标准差未知时,最小二乘法拟合是震级转换最优的选择.对于固定地震台网与流动地震台网的震级标度不一致的情况,若想得到地震的真实震级,可先通过不同震级标度之间相互转换的经验公式获得相同类型的震级数据,再进行震级矫正计算.但不同震级标度转换公式的选择至关重要,错误的震级转换关系可能会导致较大的转换误差,这可能会对地震危险估计和震级-频度关系的确定造成严重影响(Castellaro and Bormann, 2007; Pandey et al., 2017).因此,如何进一步提高本文发展的算法在应用上的普适性,或可同时考虑不同震级标度下的真实震级的确定,这是未来需进一步探讨的问题.
4 结论
在稀疏的固定地震台网内增设的一个或多个流动地震台网时,受到地震记录信噪比低、难以获得准确的台基校正项等多种因素影响,使得分别用固定地震台网和流动地震台网测定的震级往往存在显著差异.为将固定地震台网与流动地震台网的地震记录融合利用,矫正并估计真实震级,本文基于固定地震台网测定震级误差小于流动地震台网的先验性假设,利用震级偏差的概率密度函数,并将不同地震台网测定震级的标准差作为权重,构建了固定地震台网分别与一个或多个流动地震台网进行融合和矫正震级的算法.将该算法应用于中国四川省西昌市布设的流动地震台网与当地稀疏分布的中国固定地震台网记录数据融合和获得真实震级的案例,验证了该方法的可行性.本文获得的主要认识如下:
(1)本文所发展的基于贝叶斯公式的震级矫正算法,是以地震台网测定的震级误差为基础,针对固定台网和流动台网的震级测定差异,可综合考虑震级的人工测定误差、台站台基状态、震级量规函数等因素,得到相对客观的矫正震级.通过矫正震级与原始测定震级的对比,还可得到地震台网测定震级的误差偏移情况,为实际的科学研究提供参考.
(2)本文所提出的基于贝叶斯公式的震级矫正方法可适用于同一区域布设多个流动地震台网、分别独立测定震级的情况.只需提前了解地震事件被哪些地震台网同时记录到,按照多地震台网的矫正震级计算公式,即可得到多台网布设情况下的矫正震级及矫正参数.对于只有一个台网记录的地震事件,则基于固定台网与流动台网的线性回归关系,带入矫正参数,直接进行单台网记录地震事件的震级矫正.随着参与震级矫正的地震台网的不断增多,多地震台网的震级矫正方法可得到更为科学合理的地震震级,应用潜力较大.
(3)由理论结果和数据分析可以看出,本文提出的方法并非简单地迁就标准的固定地震台网的测定震级结果.当流动地震台网的震级矫正参数有了稳定的估计值后,可以利用流动地震台网的测量结果,反过来能获得比固定地震台网测定精度更高的震级估计值.
(4)对西昌流动地震台网测定震级结果的分析表明,西昌流动地震台网测定震级整体偏小,固定地震台网测定震级与最终的矫正震级之间存在一定偏离度的线性关系.对于西昌地区,利用本文的震级矫正算法并结合获得的震级矫正参数表,可实现对未来新发生地震的快速震级矫正并得到矫正震级的大小.
致谢本文使用的西昌地震台阵的地震目录和地震观测报告由中国地震局地球物理研究所房立华研究员提供,本项研究主要的理论研究部分是第一作者在访问日本统计数理研究所(ISM)期间完成,ISM为本研究提供了计算和办公等条件支持,在此一并表示感谢.
附录A 真实震级概率密度函数的推导过程
由(8)式可得,给定m1和m2情况下的真实震级m所满足的概率密度函数正比于分子部分,因此可将(8)式的分子部分转化为真实震级m所满足的正态分布表达形式,即可对应的得到真实震级m的均值μ及标准差σ2.将(3)(5)式代入(8)式的分子部分,
(A1)
为了易于对(A1)式关于m进行积分以求解μ和σ2,令
(A2)
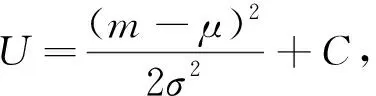
(A3)

(A4)
将(A4)式中的μ代入(A2)式的m,可得到U的极小值Umin.

(A5)
因此(A2)式可以写为

(A6)
由此可得到给定固定台网震级分布m1,及一个流动台网m2,最终所得到的真实震级概率密度函数的表达式为

(A7)


附录B 多台网观测时真实震级服从的条件分布的推导
当有k个台网时,即存在一个固定台网及k-1个流动台网,真实震级服从的条件分布表达形式推导过程如下:
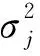
(B1)
真实震级m的概率密度函数为
(B2)
由于固定台网和流动台网的震级记录在给定真实震级m的条件下是相互独立的,且不同流动台网之间的震级记录相互独立,则当2≤j≤k时,
fj|·1…j-1(mj|m,m1,…,mj-1)=fj|·(mj|m),
(B3)
fj|1…j-1(mj|m1,…,mk-1)=fj|1(mj|m1).
(B4)
根据全概率公式,给定固定台网震级m1条件下流动台网震级mj的条件概率密度函数为
f2…k|1(m2,…,mk|m1)=
(B5)
将(B3)、(B4)和(B5)式代入(B2)式,则
f·|12…k(m|m1,m2,…,mk)=
(B6)
(B6)式中的分布为一个正态分布,设k个地震台网下,真实震级均值为μ,标准差为σ2,即
(B7)
将k个地震台网所满足的概率密度函数代入(B6)式的分子部分,
(B8)
为了易于对(B8)式关于m进行积分以求解μ和σ2,令

(B9)

(B10)

(B11)


(B12)
由此可得,存在一个固定台网及k-1个流动台网(j=k)时,真实震级服从的条件分布为均值为
(B13)
而方差为
(B14)
的正态分布.至此,正文部分(12)式、(13)式得证.
