基于Lanczos-模型降阶算法的三维频率域可控源电磁快速正演

刘寄仁， 汤井田,2,3,4*， 任政勇,2,3,4， 张继锋

1 中南大学地球科学与信息物理学院， 长沙 410083 2 中南大学有色金属成矿预测与地质环境监测教育部重点实验室， 长沙 410083 3 有色资源与地质灾害探查湖南省重点实验室， 长沙 410083 4 自然资源部覆盖区深部资源勘查工程技术创新中心， 合肥 230001 5 长安大学地质工程与测绘学院， 西安 710061

0 引言

陆地可控源电磁目前被广泛应用于矿产资源、天然气、煤田采空区富水性调查等环境与工程地球物理领域(汤井田和何继善, 2005).正演模拟可以为研究实际地质响应特征提供参照，因此需要开发快速的三维正演计算方法.

陆地可控源电磁的主流正演方法有积分方程法(Avdeev et al., 2002; Zhdanov et al., 2006; 任政勇等, 2017; 汤井田等, 2018)、有限差分法(Mackie et al., 1994; Newman and Alumbaugh, 2002; Streich, 2009; Malovichko et al., 2019)、有限体积法(Jahandari and Farquharson, 2014, 2015; Peng et al., 2018; Liu et al., 2019)、有限单元法(Mitsuhata and Uchida, 2004; Schwarzbach et al., 2011; Ren et al., 2013, 2014; Grayver and Kolev, 2015; Um et al., 2017; Liu et al., 2018).有限单元法近年来得到了广泛的应用，主要因为它具有理论体系成熟、网格剖分灵活等特点，结合非结构化网格可以模拟复杂地形及地质结构，便于在场源、测点及电性分界面处进行网格加密，从而提高数值计算的精度.有限单元法正演可以采用总场公式和二次场公式.总场公式需要对场源附近的电磁场做精细处理，并且在计算边界上需要施加精细的边界条件，但总场公式能够有效模拟任意起伏地形(李建慧等, 2016; 邱长凯等, 2018).二次场公式的模拟变量为散射场，散射场在源附近一般不再具有奇异性，因此具有模拟精度高的特点，但是二次场公式需要背景模型具有解析的一次场表达式(张林成等, 2017).一般来说, 地形背景模型不具备解析的一次场表达式，二次场公式处理地形存在困难.因此，本文选择总场公式作为开发可处理任意起伏地形情况的陆地可控源电磁快速正演方法.

陆地可控源电磁有限元正演最终形成一个大型的复系数方程组.该方程组和频率有关，各频点之间相互独立，可以使用基于频点的CPU并行求解技术来实现加速，但该加速方案受限于计算机硬件设备.另一种方案是对初始线性方程组的系数矩阵进行降阶，在保留系统性质的基础上，通过降阶手段，使用一个较小的系统来近似该矩阵，从而得到一个近似解.Krylov子空间投影算法是一类典型的模型降阶算法，通过构建Krylov子空间的正交基，将初始矩阵投影到子空间上，得到一个较小维度的降阶矩阵，使用该降阶矩阵来替代初始矩阵，便可以得到初始线性方程组的近似解.早期，基于m维多项式Krylov子空间的SLDM(spectral Lanczos decomposition method)方法被应用到计算电磁领域(Druskin and Knizhnerman, 1988, 1994)，但是这种多项式Krylov方法不稳定，收敛速度依赖于频率范围和模型的电导率反差，需要一个较大的m维子空间才能保证误差收敛到较小的水平，同时随着子空间维度m的增大，误差会进一步积累.为解决大型稀疏矩阵的特征值问题，Ruhe (1984,1994)提出了基于有理函数的Krylov子空间方法，与多项式Krylov子空间方法相比，该方法更加稳定，所需的子空间维度较小，能够减小计算量.

在地球物理领域中，Druskin等(2009)和Knizhnerman等(2009)通过误差分析理论，分别提出了时间域和频率域的有理Krylov子空间的多极点选择方案，其优点是收敛误差不依赖于模型的电导率反差，但对于m维的子空间，需要进行m次矩阵方程求解，如何高效的求解这些方程直接决定了有理Krylov子空间模型降阶算法的效率.为减少极点的个数，加快子空间的构建，Börner等(2008)通过选择较少的参考极点构建有理Krylov子空间，使用间接法求解时间域瞬变电磁问题，在一定精度条件下，大大提高了求解效率.Börner等(2015)提出了替代最优化算法，给出了一定时间范围内的极点选择方案，使用基于非结构化网格的矢量有限元方法实现了时间域瞬变电磁的快速正演求解.Qiu等(2019)对于宽时间范围的双极点选择方案进行了修正，使用块Krylov方法，实现了时间域海洋可控源电磁的快速正演计算，有效的提高了多源正演模拟的速度.为实现频率域可控源电磁法的快速正演求解，周建美等(2018)使用单极点模型降阶算法，结合拟态有限体积进行了三维海洋可控源电磁法的模拟.张继锋等(2020)使用单极点模型降阶算法，结合六面体节点有限元进行了陆地CSAMT的正演求解，但是误差较大，且六面体网格不适合模拟复杂地形和不规则地质体.此外，正交化算法也是影响计算效率的重要因素之一.在构建Krylov子空间的正交基时，常使用Arnoldi正交化算法(Börner et al., 2008, 2015;周建美等, 2018; 张继锋等, 2020)，虽然该算法较稳定，但是当子空间的维数增加时，需要进行大量的大型矩阵向量乘积运算，乘积运算的次数随着子空间的维度数呈平方增加，严重影响计算效率.而Lanczos算法的矩阵向量乘积的次数随着子空间维度呈线性增长，因此使用Lanczos算法能够更加快速的构建Krylov子空间的正交基.

为加快多频正演的求解速度，本文结合基于非结构化网格的矢量有限元方法和单极点模型降阶算法，使用Lanczos算法构建子空间的正交基，实现了三维陆地多频可控源电磁的快速正演.首先，采用非结构化网格进行空间离散，得到了有限元线性方程组.然后选择一定频率范围内的单个最优化极点，将大型稀疏复系数方程组的求解问题，转化为实数方程组求解，使用Lanczos算法高效的构建了有理Krylov子空间的正交基，求得初始矩阵在Krylov子空间上的正交投影.投影矩阵能适应所有频率的计算，其维数是远小于初始矩阵的，因此使用投影矩阵来替代初始矩阵，可以实现矩阵方程的快速求解.最后通过一维层状模型和三维块状体模型进行了加速比测试，给出了本文算法的精度对比，并且详细的给出了整个过程的运算时间对比和内存消耗对比，验证了本文算法具有计算资源占用率低的优势.

1 方法

1.1 CSEM有限元线性方程组

设时间谐变因子为eiω t，电场强度E的微分控制方程为：

(1)

为求解式(1)，Börner等(2008)使用基于非结构化网格的矢量有限元法结合有理Krylov子空间模型降阶算法得到了近似解，但该方法在高频和低频部分误差较大，这虽然可以通过调整极点的位置和个数来改善，但无疑会增加矩阵分解的次数，从而增加计算消耗.周建美等(2018)和张继锋等(2020)通过单极点模型降阶算法，分别使用拟态有限体积法和六面体节点有限元法实现了一定频率范围内的快速求解.本文使用基于非结构化网格的矢量有限元法和单极点模型降阶算法来对式(1)进行快速求解.

首先，采用开源的非结构化四面体网格剖分器Tetgen(Si, 2015)将计算区域剖分成多个互斥的四面体单元.然后,以图1所示的四面体单元为例，单元内部的电场值可以通过如下的线性插值公式表示:

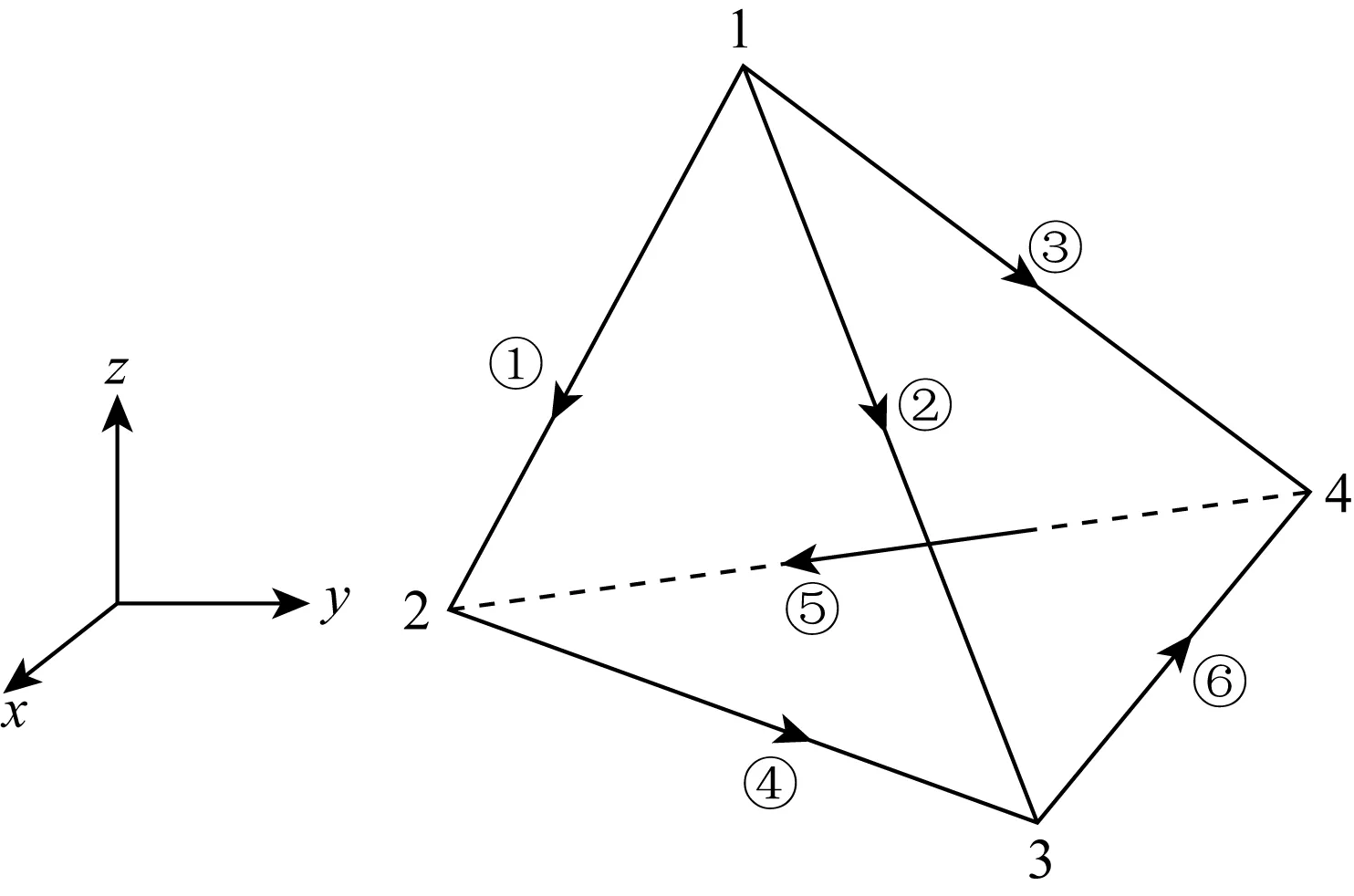
图1 四面体单元Fig.1 Tetrahedral element

(2)

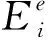
(3)

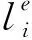
(4)

将(2)式代入(4)式，利用矢量恒等变换，并假设网格边界取得足够远，忽略边界积分项，可得：

(5)

对于任意单元e，可将式(5)写成矩阵的形式：

Re=(Ce+iωMe)Ee+iωbe,

(6)

(C+iωM)E=-iωb,

(7)

(7)式便是有限元分析最终得到的大型线性方程组，其系数矩阵为大型复数稀疏矩阵.对于多频点问题，必须进行多次矩阵方程的求解，需要消耗大量的计算内存和运算时间，严重影响正演计算的效率.

1.2 基于模型降阶的多频线性方程组加速

为了提高多频可控源电磁的正演效率，本文引入一种不依赖于频点个数的有理Krylov子空间模型降阶算法，在一定精度条件下，该算法只需要一次矩阵分解，便可对系统矩阵实现降阶，从而达到对方程组进行快速求解的目的(Güttel, 2010, 2013; Zhou et al., 2018b, 2020;周建美等, 2018; 张继锋等, 2020).对式(7)做一个简单的变形，令A=M-1C，X=M-1b，方程的解E可写为：

E=-iω(A+iωI)-1X=f(A)X.

(8)

为解决此类形如f(A)X的问题，构建有理Krylov子空间为：

(9)

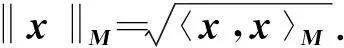
(10)

(11)

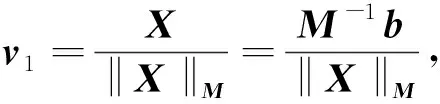
E≈‖X‖MVm+1f(Am+1)e1,

(12)

其中e1=[1,0,0,…,0]T∈m+1.可以发现，一旦求得降阶矩阵Am+1，那么f(Am+1)是容易求解的，对于多频问题，求解式(12)是快速的.

构建上述有理Krylov子空间的正交基的方法有两种，一种是Arnoldi正交化算法，该算法较稳定，但是每生成一个正交基向量需要和已生成的所有基向量进行正交，我们在式(10)中已经给出了构建正交基的递归表达式.另一种方法是Lanczos算法，虽然Lanczos算法可能会不稳定，但仍然会对初始矩阵形成有效的近似(Druskin and Remis, 2013)，每生成一个正交基向量只需利用已生成的两个基向量进行运算.其正交基的递归表达式为：

vj+1=((A-ξjI)-1vj-αjvj-βj-1vj-1)/βj

=((C-ξjM)-1Mvj-αjvj-βj-1vj-1)/βj,(13)

其中αj=(Mvj)T(C-ξjM)-1Mvj，β0v0=0，βj=‖(C-ξjM)-1Mvj-αjvj-βj-1vj-1‖M.利用M正交投影，同样可以得到式(8)的近似表达式(12).相对Arnoldi算法而言，Lanczos算法中大型矩阵向量的乘积运算次数大大减少，可以提高构建正交基的效率，因此本文选择Lanczos算法来构建正交基，算法的详细过程在表1中给出.

表1 基于M正交的Lanczos算法Table 1 Lanczos algorithm based on M-orthogonal

从表1可以看出，模型降阶算法将原来的复系数方程组求解转换为实系数方程组的求解，这显然可以提高运算效率和节省内存，但正交基的构建需要选择不同的实数极点ξj，这带来的一个问题便是需要进行多次矩阵方程的求解.位移求逆技术(Moret and Novati, 2004)是一种特殊的有理Krylov子空间模型降阶方法，其仅需选择一个重复极点满足：ξ0=ξj<0,ξ0∉Λ(A).这种单极点模型降阶算法只需要一次Cholesky分解，多次矩阵回代，便可快速构建子空间.因此本文选择单极点模型降阶算法来减少矩阵方程的求解次数，只需在表1中第03步j=1时做一次Cholesky分解，并将矩阵分解的结果保存，之后的循环只需调用即可.

(14)

2 数值实验

本文进行数值模拟的计算环境为：Ubuntu 18.04和Intel Visual Fortran 19.1,硬件为：Intel(R) Core(TM) i7-9750H CPU @2.60 GHz 2.59 GHz，16 GB个人PC机.

2.1 加速比测试

2.1.1 一维模型

为验证本文算法的正确性和高效性，首先构建一维层状模型，第一层电阻率为100 Ωm，厚度为1000 m，第二层电阻率为500 Ωm.场源的中心设置在坐标原点，沿着x轴放置，长度为100 m，电流大小为10 A.发射频率为1～10000 Hz对数等间隔分布的100个频点.使用Tetgen(Si, 2015)进行网格剖分，未知数为629370.

使用本文算法进行正演计算(3DMOR_Lanczos)，同一维解析解(1D solution)、常规有限元求解(3DFEM)、基于Arnoldi方法的模型降阶求解(3DMOR_Arnoldi)进行精度和时间对比.3DMOR_Lanczos和3DMOR_Arnoldi构建Krylov子空间的维数均为120.图2给出了测点为(0 m,-4000 m,0 m)处电场Ex的响应曲线及相对误差曲线.从图中可以看出，3DMOR_Lanczos同其他两种方法的Ex响应曲线均吻合较好，同一维解析解之间的最大误差不超过3%，验证了本文算法的正确性.3DMOR_Lanczos同3DFEM、3DMOR_Arnoldi之间的相对误差很小，说明3DMOR _Lanczos对3DFEM的近似效果较好，且与Arnoldi方法的结果吻合.在y轴上布置一条测线，起始位置为(0 m,-5000 m,0 m)，终止位置为(0 m,-100 m,0 m)，图3中呈现的是105 Hz时测线上的Ex响应的变化.从中可知，3DMOR_Lanczos同1D solution之间的最大误差小于3%，同3DFEM、3DMOR_Arnoldi之间的误差很小，进一步验证了本文算法的正确性.表2给出了计算资源消耗的对比.加速比定义为其他方法与本文算法(3DMOR_Lanczos)的运算时间的比值.本文算法将复数矩阵转变为实数矩阵求解，因此与3DFEM相比，3DMOR_Lanczos消耗的内存更少，且计算时间大幅减少，加速比达到了24.9.与3DMOR_Arnoldi相比，二者消耗的内存相近，但加速比达到了2.7，表明了本文算法的高效率.

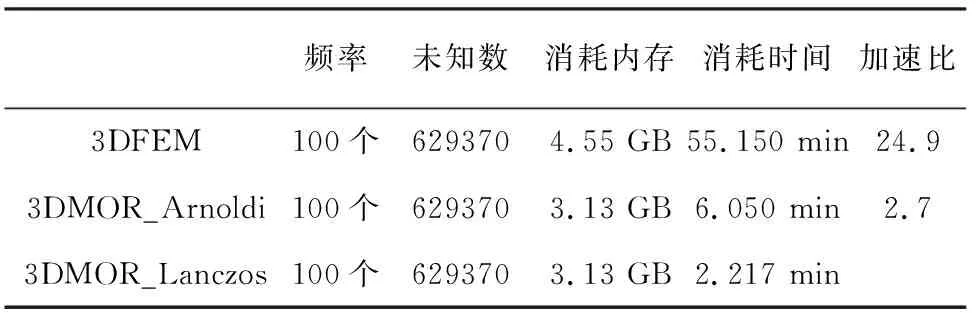
表2 运算时间对比Table 2 Comparison of calculation time

表3给出了3DMOR_Lanczos和3DMOR_Arnoldi的运行时间分布，由于矩阵的规模较小，结合Lanczos算法的高效性，Pardiso矩阵分解和构建正交基消耗的时间占比仅为40.6%，最终的频点运算消耗了大部分的运算时间.3DMOR_Lanczos和3DMOR_Arnoldi两种算法的唯一不同在于正交基的构建方法不一样，我们注意到，3DMOR_Arnoldi的正交基构建占据了整个过程的66.39%，这说明使用Lanczos算法构建正交基更加高效.为方便说明和阅读，后文将3DMOR_Lanczos缩写为3DMOR.

表3 3DMOR的运算时间分布Table 3 Calculation time distribution of 3DMOR

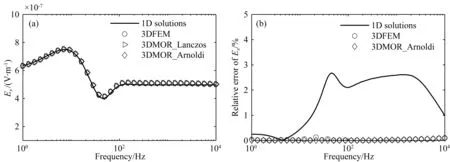
图2 3DMOR_Lanczos同1D solution、3DFEM、3DMOR_Arnoldi的测深曲线对比(a) 不同算法的Ex响应对比图; (b) 3DMOR_Lanczos同其他方法之间的相对误差.Fig.2 Comparison of sounding curves of 3DMOR_Lanczos with 1D solution, 3DFEM and 3DMOR_Arnoldi(a) Comparison of Ex responses of different algorithms; (b) The relative error between 3DMOR_Lanczos and other methods.

图3 频率为105 Hz时, 3DMOR_Lanczos同1D solution、3DFEM、3DMOR_Arnoldi对比(a) 不同算法的Ex响应对比图; (b) 3DMOR_Lanczos同其他方法之间的相对误差.Fig.3 Comparison of 3DMOR_Lanczos with 1D solution, 3DFEM and 3DMOR_Arnoldi at 105 Hz(a) Comparison of Ex responses of different algorithms; (b) The relative error between 3DMOR_Lancozs and other methods.

2.1.2 三维模型

为进一步说明本文算法的高效性和对三维模型的适应性，设计如图4所示的三维模型进行对比测试.图4a为模型的剖面图，图4b为模型的平面图，图中虚线为测线.在电阻率为50 Ωm的均匀半空间中嵌入一个大小为120 m×200 m×400 m的低阻异常体，其中心坐标为(1000 m,0 m,300 m)，电阻率为5 Ωm.100 m长的源沿着x轴放置，源的中心坐标为(50 m,0 m,0 m)，发射电流为1 A，发射频率为1～10000 Hz对数等间隔分布的32个频点.网格离散所形成的未知数为889023.

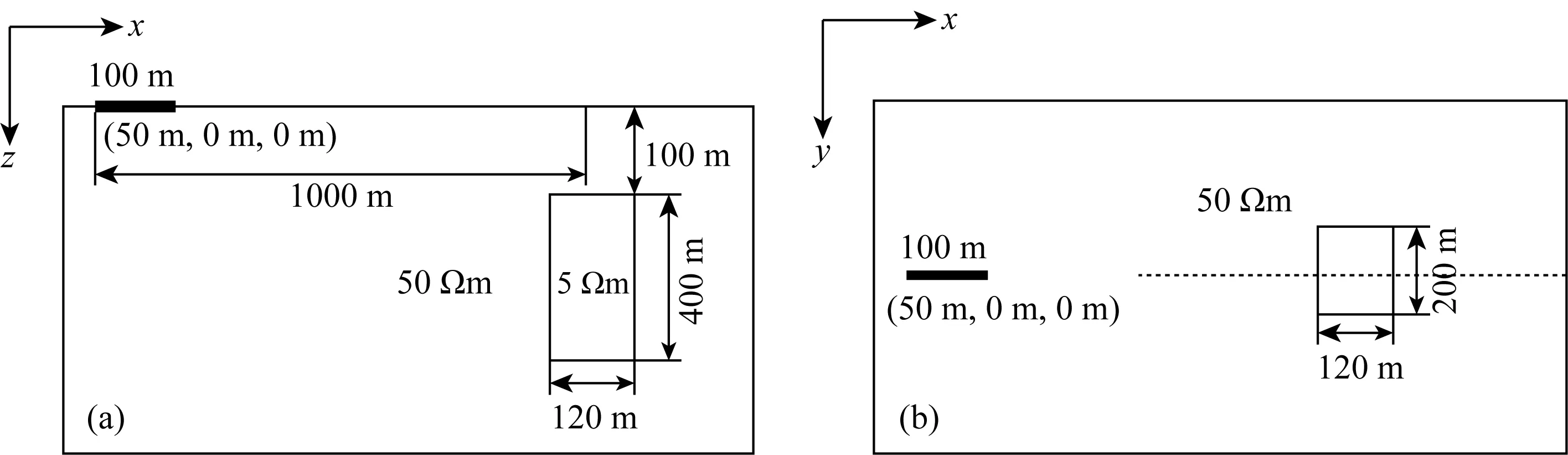
图4 三维低阻体模型示意图(a) 模型的剖面图; (b) 模型的平面图.Fig.4 Sketch of 3D low resistance body(a) Section view of the model; (b) Plan view of the model.

将本文数值解(3DMOR)与常规有限元方法(3DFEM)、基于磁矢势的有限元方法(FE)(Ansari and Farquharson, 2014)、积分方程法(IE)(Farquharson and Oldenburg, 2002; Zhou et al., 2018a)的数值解进行了Ex实部和虚部响应曲线的对比，正演计算频率为3 Hz，如图5a、图6a所示.从图中可知，由于地下低阻体的存在，地下电流被低阻体“吸引”，导致地表的电流密度降低，从而出现了电场Ex响应的实部和虚部曲线在x为900～1100 m范围内均呈现向下凹陷现象.图5b和图6b给出了Ex响应的相对误差曲线，除IE方法外，本文算法同其他两种方法之间的相对误差未超过3%，这说明利用本文算法进行三维模型的正演是可行的.

图5 频率为3 Hz时, 3DMOR同多种数值模拟方法的电场实部的对比(a) 不同算法的Ex实分量对比图; (b) 3DMOR同其他方法之间的相对误差.Fig.5 Comparison of the real part of electric field between 3DMOR and other numerical methods at 3 Hz(a) Comparison of the real part of Ex responses of different algorithms; (b) The relative error between 3DMOR and other methods.

图6 频率为3 Hz时, 3DMOR同多种数值模拟方法的电场虚部的对比(a) 不同算法的Ex虚分量对比图; (b) 3DMOR同其他方法之间的相对误差.Fig.6 Comparison of the imaginary part of electric field between 3DMOR and other numerical methods at 3 Hz(a) Comparison of the imaginary part of Ex responses of different algorithms; (b) The relative error between 3DMOR and other methods.

图7给出了测点(1000 m,0 m,0 m)处3DMOR和3DFEM的Ex响应曲线及相对误差曲线，可以看出3DMOR对3DFEM的近似效果较好.同样在表4给出了计算资源消耗的对比，从中可知加速比达到了17.6.与表2相比可知，随着未知数的增加，3DMOR更节省内存.通过表3我们可以发现，随着未知数的增加，矩阵分解和正交化过程将消耗大部分的运算时间，因此本文采用的高效的Lanczos正交化算法是可以提升正演计算效率的.

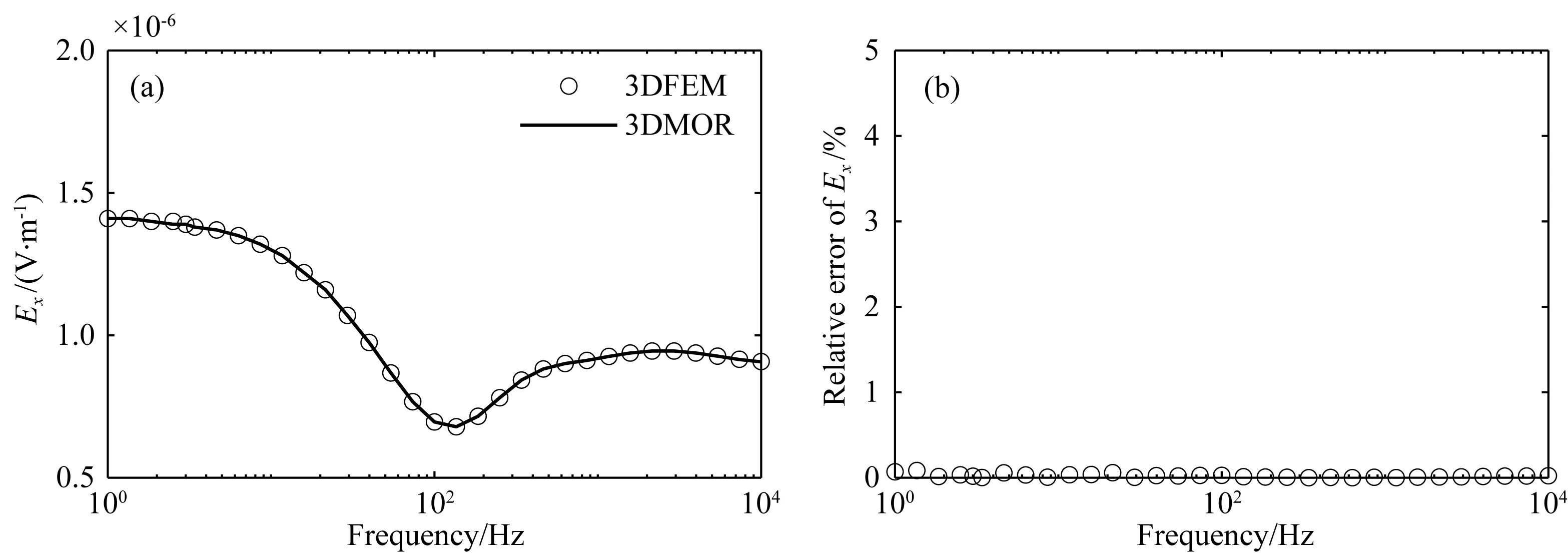
图7 中心测点的测深曲线，3DMOR同3DFEM的对比(a) 两种算法的Ex响应对比图; (b) 3DMOR同3DFEM之间的相对误差.Fig.7 Sounding curve of central measuring point, comparison between 3DMOR and 3DFEM(a) Comparison of Ex responses of two algorithms; (b) The relative error between 3DMOR and 3DFEM.

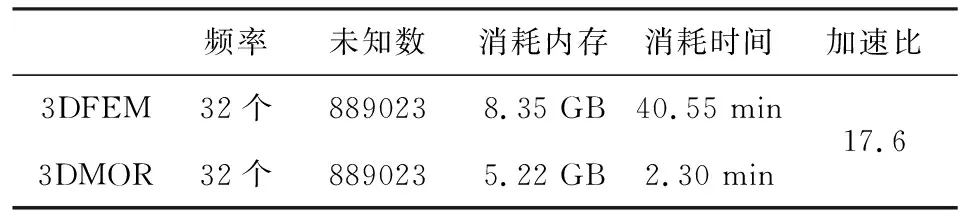
表4 运算时间对比Table 4 Comparison of calculation time

2.2 频率分段策略

为适应更宽频的可控源电磁的正演计算，首先需要探究频带宽度和Krylov子空间维度对求解精度和速度的影响.基于上文的1D层状模型，固定最高频率为10000 Hz，保持正演计算频率的数量不变，逐步改变频率的范围和Krylov子空间维度m，fmax表示最高频率，fmin表示最低频率，利用式(14)得到了图8所示的误差曲线和运算时间分布图.从图8a可以看出，当频带范围越小时，整体误差收敛的速度越快，只需要构建较小的Krylov子空间便能达到较高的精度.而从图8b所示的计算时间分布上也可以看出，由于只改变了Krylov子空间的维度，因此四条曲线的变化趋势是吻合的.随着Krylov子空间维度的增加，运行时间基本呈现线性增长，这是Lanczos算法的计算优势.

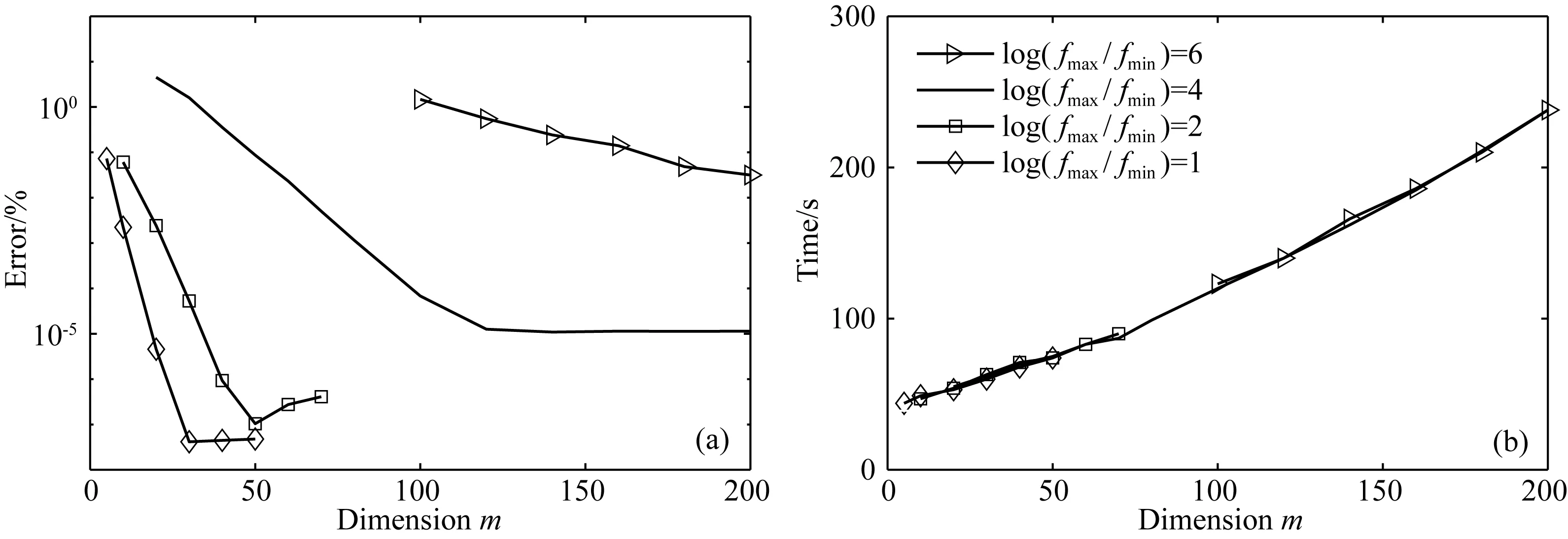
图8 不同频带宽度下，3DMOR的(a)整体误差和(b)运行时间随Krylov子空间维度的变化Fig.8 Under different bandwidth, (a) the overall error and (b) the running time of 3DMOR change with the dimension of Krylov subspace

在频率域可控源电磁的正演计算中，当发射频率的范围较大时，为控制高频和低频的精度，不仅要求浅部的网格剖分更精细，还要求网格边界取得足够远.特别是对于层状介质而言，网格单元数量增长很快，会浪费一定的计算资源.在使用3DMOR进行宽频正演计算时，基于Krylov子空间维度较大和网格单元较多这两个特征，本文提出频率分段策略：针对宽频问题(log(fmax/fmin)>4)，对频率进行分段，同时输入两套网格，使用并行算法进行3DMOR的运算.这不仅可以减小矩阵方程的规模，还可以减小Krylov子空间的维度，加快误差的收敛速度.

对于上述的1D层状模型，扩大频率计算范围为0.01～10000 Hz，正演计算100个频率，测点坐标为(0 m,-4000 m,0 m).改变Krylov子空间的维数m，其余参数保持不变.图9给出了四种不同的Krylov子空间维度下的Ex响应曲线.可以发现3DMOR在高频段的Ex响应出现了波动,m需要达到200才能和1D solution 曲线呈现较好的吻合，此时的运算时间为240 s.虽然随着Krylov子空间维度的增加，误差会逐步减小，但无论是选择式(10)所示的Arnoldi算法还是式(13)描述的Lanczos算法，过大的子空间需求都会增加构建正交基的计算量，影响计算效率.

图9 当频率计算范围为[0.01,10000]Hz时，3DMOR采取不同Krylov子空间维度的测深曲线同1D solution对比Fig.9 When the frequency calculation range is [0.01,10000] Hz, the sounding curves of 3DMOR with different Krylov subspace dimensions are compared with 1D solution

我们使用频率分段策略来解决这一问题.对于高频部分，设置网格边界为±20 km，方程未知数为356637，构建Krylov子空间的维度为80.对于低频部分，设置网格边界为±150 km，方程未知数为348119，同样构建Krylov子空间的维度为80.最终总内存消耗为3.33 GB，总运行时间为101 s.图10给出了进行频率分段之后的运行结果，黑色的虚线为频率分段的交界点，结果显示最大误差未超过3%，表明了本文提出的频率分段策略对于宽频可控源电磁的正演计算是可行的.

图10 当频率计算范围为[0.01,10000]Hz时，采取频率分段策略的计算结果(a) 3DMOR同1D solution的测深曲线对比; (b) 相对误差.Fig.10 Calculation results of frequency segmentation strategy when frequency calculation range is [0.01,10000]Hz(a) Comparison of sounding curve between 3DMOR and 1D solution; (b) Relative error.

2.3 三维地质体响应特征分析

设计如图11所示的三维低阻球体模型，图12为网格剖分示意图.球体的半径为200 m，中心埋深位于(0 m,5000 m,400 m)，电阻率为10 Ωm，围岩电阻率为100 Ωm.x方向的电流源放置在坐标原点，其长度为200 m，发射电流为10 A，发射频率为0.01～10000 Hz对数等间隔分布的100个频点.本例在地表布置了11条测线，线距为200 m，y坐标范围为-1000～1000 m.每条测线长度为2000 m，含11个测点，点距为200 m，x坐标范围为4000～6000 m.仍然采用上文的频率分段策略来进行正演求解.对于高频段，设置网格边界为±20 km，方程未知数为578603，构建Krylov子空间的维度为80.对于低频段，网格边界为±150 km，方程未知数为387979，构建Krylov子空间的维度为80.两套网格并行计算，最终消耗总内存为4.11 GB，总运行时间为148 s.

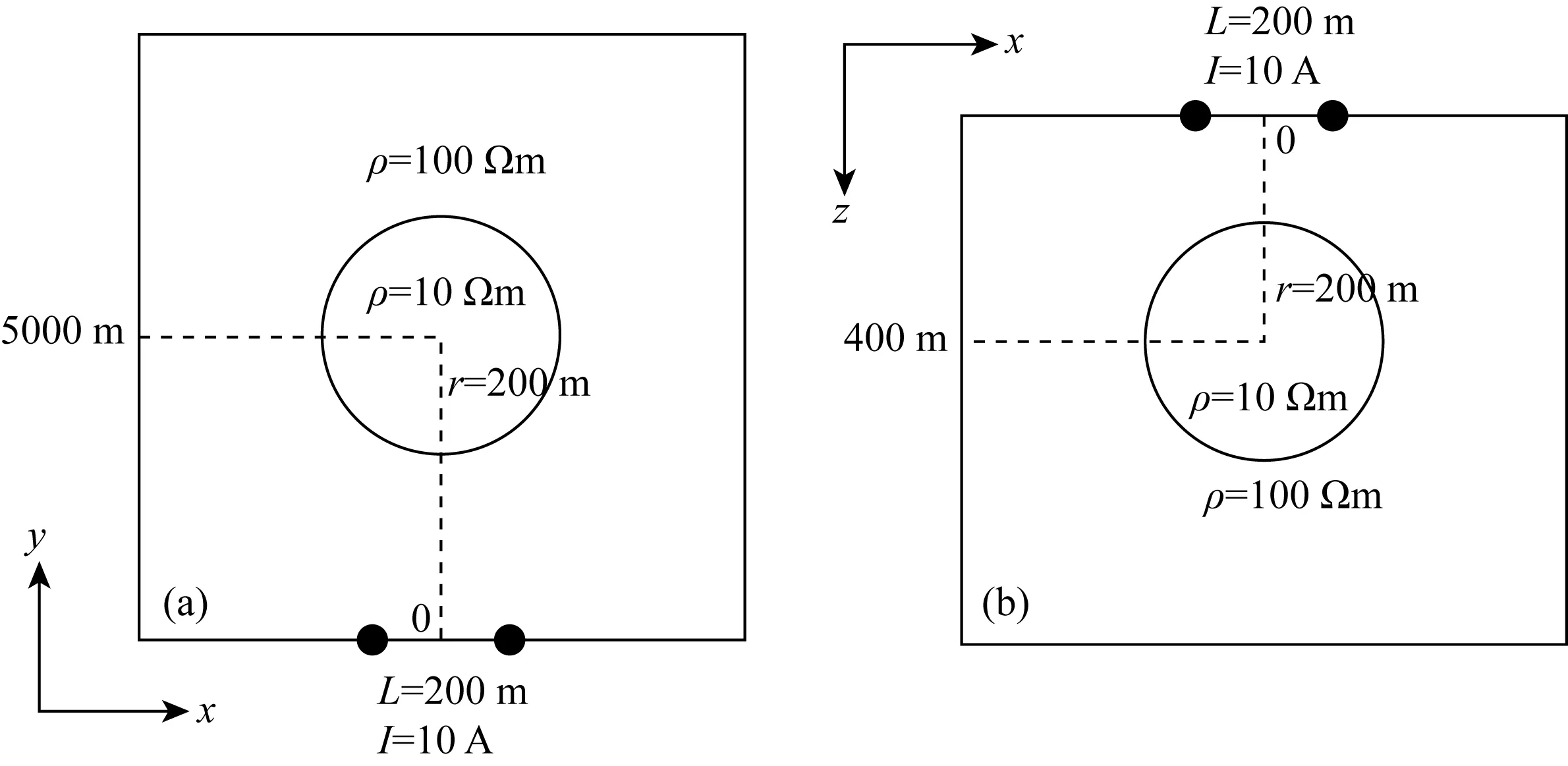
图11 三维低阻球体模型示意图(a) 模型的平面图； (b) 模型的切片图.Fig.11 Sketch of 3D low resistance sphere model(a) Plan view of the model; (b) Section view of the model.

图12 网格剖分示意图Fig.12 Schematic diagram of mesh generation

图13给出了四个频率的磁场Hy分量、电场Ex分量以及广域视电阻率的切片图，四个频率分别为10000 Hz、100 Hz、1 Hz、0.01 Hz，其中广域视电阻率利用Ex求得(李帝铨等, 2013; He, 2018;武建平等, 2020；Yu et al., 2020).从图13(a,b,c,d)中可以看出，磁场Hy分量对异常体的响应较微弱，无法从切片图中观察到异常场造成的畸变.如图13(f,g,h,j,k,l)所示，由于低阻异常体的存在，使得地表电流密度减小，因此电场Ex分量和广域视电阻率均出现凹陷，在频率为100 Hz、1 Hz、0.01 Hz均有不同程度的响应，能够较好的反映异常体的位置和属性.图14给出的是两条中心测线(x=0 m测线,y=5000 m测线)的广域视电阻率拟断面图，可以看出，在高频部分广域视电阻率趋向于背景电阻率，在低频部分呈现低阻响应形态.

图13 频率分别为10000 Hz、100 Hz、1 Hz、0.01 Hz的Hy、Ex、广域视电阻率切片图(a)—(d)磁场Hy分量切片图; (e)—(h)电场Ex分量切片图; (i)—(l)广域视电阻率切片图.Fig.13 Slices of Hy, Ex and wide field apparent resistivity with frequencies of 10000 Hz, 100 Hz, 1 Hz and 0.01 Hz respectively(a)—(d) Slices of magnetic field Hy; (e)—(h) Slices of electric field Ex; (i)—(l) Slices of wide field apparent resistivity.

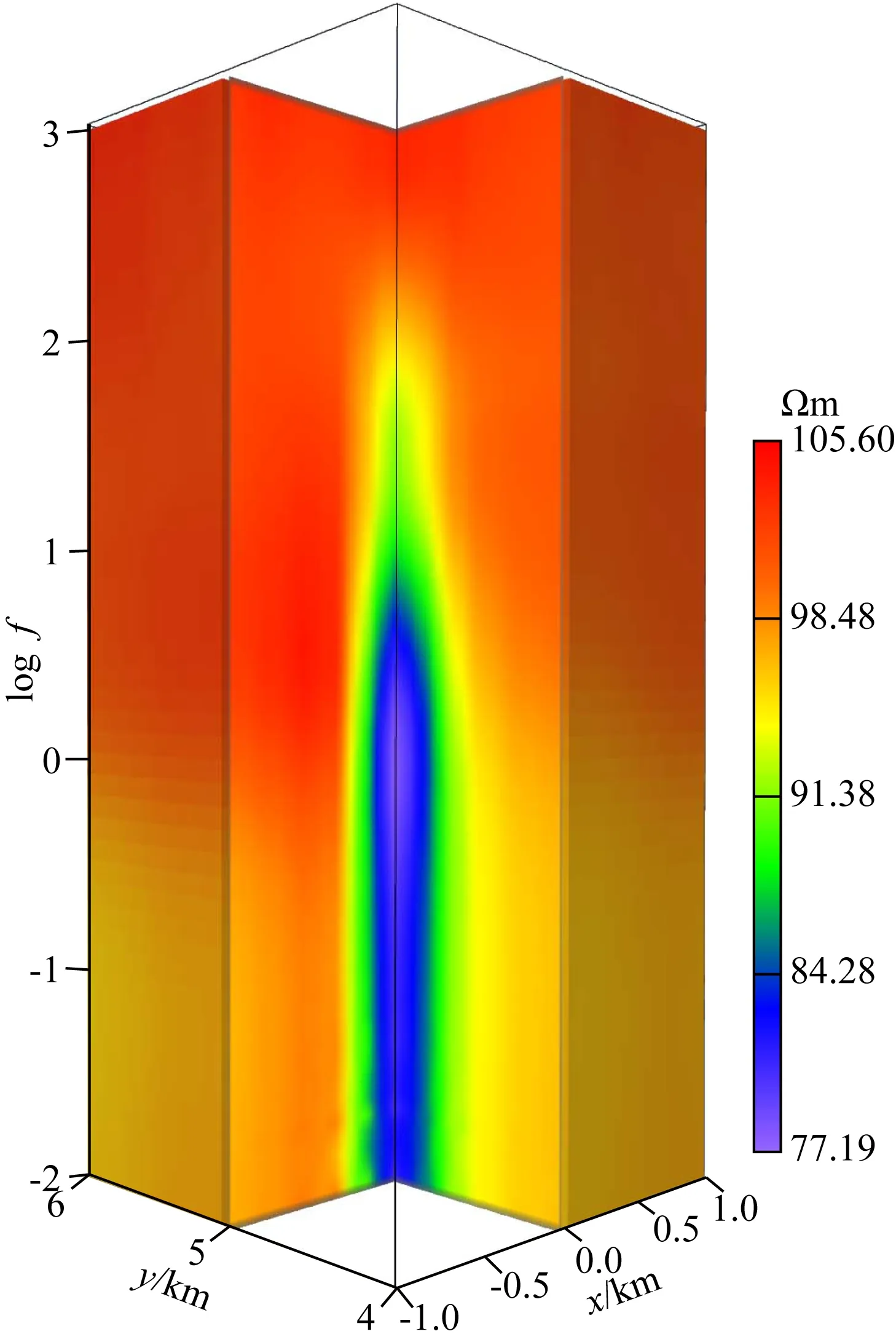
图14 x=0测线和y=5000测线的广域视电阻率拟断面图Fig.14 Pseudo-section of wide field apparent resistivity with line x=0 and line y=5000

图15给出了三个测点处的测深曲线，测点分别位于(-1000 m,5000 m,0 m)、(1000 m,5000 m,0 m)、(0 m,5000 m,0 m)，图15a为电场Ex分量的变化曲线，图15b为广域视电阻率变化曲线，黑色的虚线为频率分段的交界点.从图中可以看出，随着频率的减小，两个旁侧测点(-1000 m,5000 m,0 m)、(1000 m,5000 m,0 m)的响应基本趋于背景值，而中心测点(0 m,5000 m,0 m)处的Ex响应出现了减小，广域视电阻率曲线也呈现下降.这是由两个旁测点距低阻异常体较远，二次场响应较弱，而中心测点在低阻异常体正上方导致的.

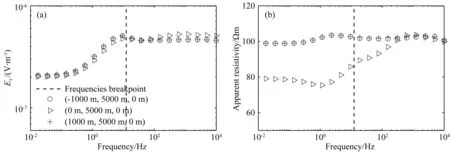
图15 测点为(-1000 m,5000 m,0 m),(0 m,5000 m,0 m),(1000 m,5000 m,0 m)的测深曲线(a) 不同测点的Ex分量对比图; (b) 不同测点的广域视电阻率对比图.Fig.15 The sounding curves at coordinates (-1000 m,5000 m,0 m), (0 m,5000 m,0 m), (1000 m,5000 m,0 m)(a) Comparison of Ex components of different measuring points; (b) Comparison of wide field apparent resistivity of different measuring points.

3 结论

本文使用单极点模型降阶算法实现了三维陆地多频可控源电磁法的快速正演.采用非结构化网格进行空间离散，结合伽辽金方法得到有限元线性方程组.选择单个最优化极点，进一步结合直接法求解器Pardiso，利用Lanczos算法快速构建Krylov子空间的正交基.将有限元线性方程组的系数矩阵投影到Krylov子空间，得到维度较小的降阶矩阵，利用降阶系统实现了多频可控源电磁的快速正演.

本文设计了一维层状模型和三维块体模型，同解析解和多种数值方法的结果进行了对比，结果表明：在满足精度要求的条件下，只需花费常规正演中计算一两个频点所消耗的时间，便可实现几十至上百个频率的快速正演，大大提高了正演计算的效率，验证了本文算法求解多频问题的高效性及其良好的三维适应性.针对宽频的问题(log(fmax/fmin)>4)，由于单极点模型降阶算法需要构建更大的Krylov子空间维度以及更高的网格需求，我们提出频率分段的策略，分别针对高频和低频部分，同时采用两套网格进行计算，这不仅可以减少网格不必要的浪费，还能加快模型降阶的收敛速度，以更小的Krylov子空间维度达到更高的精度.设计了三维球体模型，结合频率分段策略进行正演计算，数值结果表明，频率分段策略不仅能够实现正演的快速计算，还能很好的控制高频和低频的精度.值得注意的是，网格剖分需要考虑四面体网格的质量，畸变的四面体网格可能会导致病态的矩阵方程，从而影响有理Krylov子空间近似的效果.

本文开发的基于Lanczos-模型降阶算法的频率域可控源电磁正演求解器具有快速求解三维多频可控源电磁响应的能力，对于研究地质模型的三维电磁响应特征具有十分重要的意义.