仿马尾草薄壁结构的设计与耐撞性研究
2022-06-02邓敏杰刘志芳
邓敏杰,刘志芳
(太原理工大学机械与运载工程学院应用力学研究所, 山西 太原 030024)
在汽车被动安全设计中,薄壁结构因其质量轻、制造成本低、能量吸收效率高而被广泛用作能量吸收装置[1]。当汽车发生碰撞时,能量吸收器通过稳定的渐进式折叠变形耗散碰撞产生的大量能量,以保护乘客安全[2]。在过去的几十年里,人们对方形[3]、六角形[4]、八角形[5]和圆形[6]截面薄壁结构的耐撞性能进行了大量研究。Rossi 等[7]通过后屈曲变形,比较了四边形、六边形和八边形截面薄壁结构的耐撞性。Yamashita 等[8]研究了不同多边形截面空心管在单轴压缩下的耐撞性能,结果表明,截面角数会影响压缩过程中薄壁结构的承载能力。这些研究表明,截面形状对薄壁柱的耐撞性能有显著影响。
轴向加载下简单薄壁结构存在初始峰值力高、能量吸收效率低、碰撞过程不稳定等缺点[9]。为了解决这些问题,研究人员设计了多角薄壁结构[10]、多胞薄壁结构[11]以及其他截面轮廓的薄壁结构[12]。Liu 等[13]研究了星形截面管的变形模式和能量吸收特性,发现星形管的比吸能(specific energy absorption,SEA)略高于多边形管。Zhang 等[14]研究了多胞方管的能量吸收特性,证实多胞管的能量吸收效率明显高于空心单管。Sharifi 等[15]对不同的双圆管进行了轴向准静态压缩实验,发现双管比单管具有更好的能量吸收性能。杨欣等[16]通过模仿虾螯的微结构,提出了一种仿生薄壁管,通过实验和数值模拟分析了仿虾螯结构多晶胞薄壁管在不同冲击角度下的耐撞性能,发现圆管和虾螯仿生结构的结合有效地提高了仿虾螯结构多胞薄壁管的耐撞性能。Ha 等[17]提出了一种仿椰子树轮廓的新型管状波纹薄壁结构,以提高能量吸收能力、降低初始峰值力,研究发现仿生管的SEA 是正弦波纹管的2.8 倍。以上研究结果表明,自然启发的设计方法可以有效地提高薄壁结构的吸能能力。
植物茎秆具有良好的力学性能,可以适应复杂的自然环境。马尾草是多年生草本植物,生长在各种环境中。马尾草的长细比很高,但复杂的空心管状结构使其能够有效地承受重力、风、雪等环境载荷。马尾草茎秆的结构特征类似于圆柱形多胞结构,且肋板与竖直方向存在一定的夹角。这为薄壁结构设计提供了灵感。
本研究提出一种仿马尾草的新型仿生薄壁管结构,并探究其能量吸收特性。首先对双圆管和马尾草仿生薄壁管的耐撞性能进行对比研究,分析马尾草仿生薄壁管的壁厚和半径对其耐撞性能的影响,进一步探究薄壁结构的肋数、肋角以及肋厚对其耐撞性的影响,最后采用响应面法(response surface methodology,RSM)构造多项式代理模型,结合遗传算法(NSGA-Ⅱ),提出一种多目标优化方法,以优化薄壁结构的吸能性能。
1 马尾草仿生设计及防撞性评价指标
1.1 结构设计
马尾草是一种茎秆长细比很大的草本植物,其茎秆结构与普通植物不同,是由肋连接的双圆环结构,从径向截面上看,肋在沿着茎秆的延伸方向与竖直方向存在一定夹角,如图1(a)、图1(b)和图1(c)所示。根据马尾草茎秆横向和轴向截面的结构特征,提出了一种新型带倾斜肋的双圆柱薄壁管(Tube-2),同时与无肋双圆柱薄壁管(Tube-1)进行对比研究。两种管件的几何模型如图1(d)和图1(e)所示,带倾斜肋的双圆柱薄壁管任意截面上的肋通过圆心与内外管连接。两种薄壁管的管长均为H,外管和内管的壁厚均为t,外管半径为R,内管半径为r,肋厚为tL。在本研究中,所有管件的长度和外管半径为不变量,且H=100 mm,R=60 mm。用 ω 表示连接肋的倾斜程度,定义 ω=2πH/θ , 其中θ 表示上、下端面径向肋边的夹角。

图1 马尾仿生薄壁结构的设计:(a)马尾草,(b)横截面,(c)倾斜肋骨,(d)传统双圆管,(e)仿生结构Fig. 1 Design of horsetail bionic thin-walled structure: (a) horsetail, (b) cross-section,(c) inclined ribs, (d) double round tube, (e) bionic structure
1.2 防撞性评价标准
为了获得仿生薄壁结构的合理设计参数,本研究选择总吸能(energy absorption,EA)、SEA、峰值载荷(peak crushing force,PCF)、平均压缩力(mean crushing force,MCF)和压缩力效率(compression force efficiency,CFE)[18]作为薄壁结构吸能特性的评价指标。
EA 是指压缩过程中吸收的总能量,表示为


2 有限元模拟与可靠性验证
2.1 有限元模拟
利用商业有限元软件ABAQUS 建立有限元模型(finite element model,FEM),并分析马尾草仿生薄壁结构在压缩过程中的吸能特性。如图2 所示,薄壁结构上端与带有恒定挤压速度(v=10 m/s)的刚性平板接触,下端与固定约束的刚性平板接触。所有接触均定义为通用接触;切向接触属性为罚接触,罚函数系数为0.2;法向接触属性为硬接触,接触后允许分离。压缩位移为初始长度H的75%,薄壁结构的外壁、内壁和肋都用S4R 壳单元进行建模,壳单元在厚度方向上有5 个积分点。

图2 马尾草仿生薄壁结构的有限元模型Fig. 2 Finite element model of horsetail bionic thin-walled structure
马尾草仿生薄壁结构基体材料采用铝6063T5,不考虑应变率效应的影响,材料参数见表1[19],其中: ρ 为 密度, σY为 屈服应力, σu为极限应力,E为弹性模量,µ为泊松比。开展了网格敏感性分析,以研究网格尺寸对数值模拟结果精度的影响,结果如图3 所示。当网格尺寸为1.0 和0.5 mm 时,压缩过程中的力-位移曲线趋于重合。综合考虑计算资源和计算效率,将网格尺寸设置为1.0 mm。

表1 铝6063T5 的材料参数Table 1 Material parameters of Al 6063T5
2.2 可靠性验证
为了验证有限元模拟参数以及其他设置的可靠性,对文献[19]中的实验进行有限元模拟,管壁的壁厚均为1.00 mm,实验结果与模拟结果如图4所示。从图4(a)所示的力-位移曲线中可以看出,通过实验和数值模拟得到的压缩力均先出现峰值载荷,然后急剧下降,最后在某个较低值处上下波动。如图4(b)所示,有限元模拟和实验得到的薄壁双圆管变形模式均表现为轴对称模式。在渐进折叠过程中,有限元模拟与实验得到的PCF 分别为60.76 和61.37 kN,MCF 分别为23.08 和24.93 kN,两者吻合较好。

图4 实验[19]与有限元模拟结果对比:(a)力-位移曲线,(b)变形模式Fig. 4 Comparison of experimental[19] and finite element simulation results: (a) force-displacement curves, (b) deformation model

3 马尾草仿生薄壁结构的耐撞性
3.1 连接肋的影响
在改变壁厚并保证质量相同的情况下,比较了薄壁结构Tube-1 和Tube-2 的力-位移曲线,如图5 所示。在渐进折叠过程中,Tube-1 和Tube-2的力-位移曲线变化趋势一致,压缩载荷首先出现峰值载荷,然后急剧下降,最后在一个较低的载荷水平波动。薄壁结构Tube-2 的力-位移曲线位于Tube-1 的上方,说明连接肋可以提高薄壁结构的能量吸收能力;另外,Tube-2 的压缩力波动范围比Tube-1 窄,说明带肋的薄壁管在动态受压过程中可以更加稳定地吸收能量。Tube-1 和Tube-2在压缩载荷下的变形模式如图6 所示,可以看出,它们都是轴对称变形模式。如图6(b)所示,Tube-2在压缩过程中沿着连接肋的方向出现了复杂的变形模式,连接肋导致内外管变形不同步。第6 层折叠时,Tube-1 的折叠程度高于Tube-2(见图6 方框),说明连接肋可以增大折叠半波长。以上结果表明,内外壁与肋之间的相互作用可以提高薄壁结构的承载能力,也可以使仿生薄壁结构在压缩过程中以较稳定的状态吸收能量。由表2 可知,在质量相等的情况下,Tube-2 的PCF 降低了1.66%,SEA 提高了34.74%,CFE 提高了37.50%。

表2 薄壁结构的耐撞性比较Table 2 Comparison of crashworthiness of thin-walled structures

图5 薄壁结构的力-位移曲线比较Fig. 5 Comparison of force-displacement curves of the thin-walled structures

图6 薄壁结构的变形模式Fig. 6 Deformation modes of thin-walled structures
3.2 内半径和整体壁厚的影响
内半径和整体壁厚对马尾仿生薄壁结构PCF 的影响如图7(a)所示。在所有内半径取值中,随着壁厚增大,PCF 也相应增大。这是由于增加壁厚会增大结构的刚度,使得压缩过程中的PCF 增大。因此,可以通过调节薄壁结构的壁厚降低PCF,以达到更好的防护效果。PCF 随着内半径的改变呈现出较平缓的变化趋势,当内半径取最大值时,PCF 也最大。当壁厚取0.60 和0.80 mm,内半径等于30 mm 时,PCF 达到最小值;而壁厚取1.00 和1.20 mm,内半径小于35 mm 时,PCF 随内半径的增大先增大后减小:说明壁厚和内半径对PCF 产生较弱的交互作用。内半径和整体壁厚对马尾草仿生薄壁结构 SEA 的影响如图7(b)所示。内半径取任意值时,SEA 都随着壁厚的增加而单调增大。当SEA 达到较大的水平(大于29.00 J/g),即壁厚取1.00 mm 时,内半径越接近35 mm,SEA 越大;壁厚取1.20 mm 时,内半径越接近30 mm,SEA 越大。内半径最大时,SEA 最小。这可能是因为在内半径增大的过程中,连接肋的水平长度减小,致使肋与内外圆管的相互作用先增强后减弱,内半径最大时,相互作用最弱。
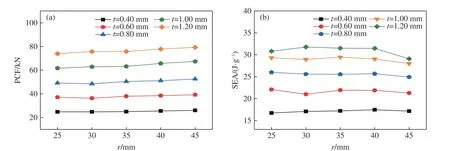
图7 内半径和壁厚对耐撞性的影响Fig. 7 Effect of inner radius and wall thickness on crashworthiness
图8 显示了不同内半径和壁厚的仿生薄壁结构在轴向压缩下的变形模式。当内半径为25 mm,壁厚为0.40 mm 时,薄壁结构出现了欧拉变形,从而降低结构的耐撞性能。内半径和壁厚较大的薄壁结构容易产生轴对称变形模式;内半径越大,变形模式越接近没有连接肋的双圆管的变形,沿着连接肋方向的复杂变形模式变得不明显。这说明增大内半径时,连接肋与内外双圆管的相互作用减弱,结构的承载能力降低。在图8 中的红色虚线与红色实线之间,薄壁结构都是非轴对称变形模式。结合各仿生薄壁结构的SEA 发现,接近轴对称模式的混合变形模式的薄壁结构的SEA 高于其他变形模式的结构。
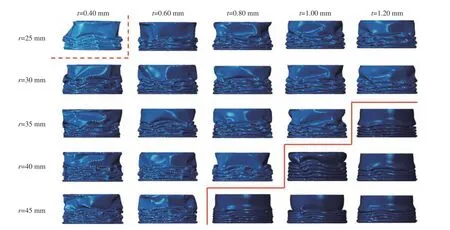
图8 不同内半径和壁厚的薄壁结构变形模式Fig. 8 Deformation modes of thin-walled structures with different internal radii and wall thicknesses
3.3 肋参数的影响
由3.1 节可知,连接肋与内外壁厚的相互作用会影响仿生薄壁结构的吸能特性,因此有必要研究肋的参数对薄壁结构吸能特性的影响。肋的参数包括肋数、肋厚和肋角。在探究连接肋数对薄壁结构耐撞性能的影响时,将内外圆管之间的肋数分别设为4、6、8、10、12,肋角保持不变,改变肋厚以确保不同肋数的仿生薄壁结构具有相同的质量。如图9 所示,PCF 随着肋数的增加而增大,但增大趋势相对平缓。SEA 随着肋数的增加而减小。随着肋数增加,肋厚减小,减弱了连接肋与内外圆管的相互作用,肋数为4 的薄壁结构具有更好的能量吸收能力。
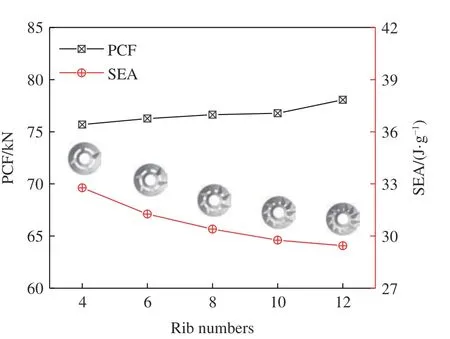
图9 不同肋数的薄壁结构的耐撞性比较Fig. 9 Comparison of crashworthiness of thin-walled structures with different ribs
肋角和肋厚对马尾草仿生薄壁结构PCF 的影响如图10(a)所示。肋角设置为16°、32°、48°、64°、80°时,PCF 随着肋厚的增加而单调增大。增大肋厚会使连接肋的刚度增大,在压缩过程中出现更大的PCF。肋角也会对PCF 产生显著的影响:当肋厚取给定值中的任意值时,随着肋角的增大,PCF 先增大后减小;当肋角为48°时,PCF 最大;肋角为80°时,PCF 最小,相比最大值减小3.70 kN。这是因为改变肋厚会影响结构的整体刚度,PCF 随着结构刚度的改变而发生相应的变化。肋角和肋厚对马尾草仿生薄壁结构SEA 的影响如图10(b)所示。可见,SEA 随着肋厚的增加而单调增大。当SEA 达到较大的水平(大于或等于31.00 J/g),即壁厚取1.20 mm 时,SEA 随着肋角改变的最大变化值为0.60 J/g。综上所述,在不改变肋厚即几乎不损失SEA 的情况下,可以通过调节肋角降低PCF,以获得最优的耐撞性能。
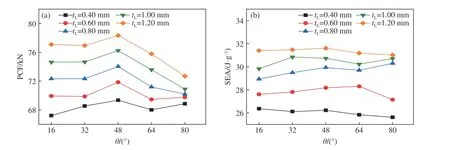
图10 肋角和肋厚对耐撞性的影响Fig. 10 Effect of degree of ribs and thickness of ribs on crashworthiness
4 耐撞性的多目标优化
4.1 优化的定义及方法
由参数分析可知,连接肋对马尾草仿生薄壁结构的耐撞性能有显著影响,与连接肋有关的参数有内半径r、肋的倾斜程度ω 以及肋厚tL,期望薄壁结构在SEA 最大化的同时,尽可能将PCF 控制在合理的范围。因此,可以将最大化SEA 和最小化PCF 作为目标函数,通过多目标优化方法研究仿生薄壁结构的耐撞性能。以内半径、肋的倾斜程度和肋厚为设计参数(单位mm),则多目标优化问题表示为

多目标优化方案如图11 所示。首先采用全因子设计方法,在设计变量范围内选取样本点;然后,采用RSM,根据有限元模拟得到的样本数据建立PCF 和SEA 的代理模型;接着,对代理模型进行评估;最后,采用NSGA-Ⅱ算法进行参数优化,得到多目标优化问题的Pareto 前沿。

图11 优化方法流程图Fig. 11 Flowchart of the optimization method


为得到PCF 和SEA 两个目标函数的最优解,采用NSGA-Ⅱ多目标优化算法得到Pareto 前沿。NSGA-Ⅱ算法拥有良好的探索性能,可增强Pareto 的前进能力,是一种解决多目标优化问题的有效算法[23]。
4.2 优化结果分析
最终得到的Pareto 前沿如图12 所示,蓝色散点为NSGA-Ⅱ算法得到的数据。当SEA 增大时,PCF 也增大,两个优化目标相互冲突。如表3 所示,选取2 个合适的参数设计Opt1 和Opt2,有限元模拟与多项式代理模型得到的结果显示,PCF 和SEA 的最大误差分别为1.28%和3.35%,说明优化结果具有合理的精度。当仅要求SEA 最大化时,最佳参数设计点为Opt2,此时SEA 为32.29 J/g,PCF 为78.60 kN,内半径为14.68 mm,肋角为10.10°,肋的厚度为1.20 mm。采用相同的参数,有限元模拟得到的SEA 为32.95 J/g,PCF 为78.49 kN,与最初设计的马尾草仿生薄壁结构相比,SEA 增加了13.42%,PCF 增加了16.43%。为了平衡SEA 和PCF 的冲突,可以选择参数设计Opt1,此时SEA 为31.49 J/g,PCF 为72.81 kN,内半径为12.25 mm,肋角为84.35°,肋的厚度为1.20 mm。在参数相同的情况下,有限元模拟得到的SEA 为30.47 J/g,PCF 为72.02 kN。与Opt2 相比,Opt1 的SEA 减小了7.52%,PCF 减小了8.24%。
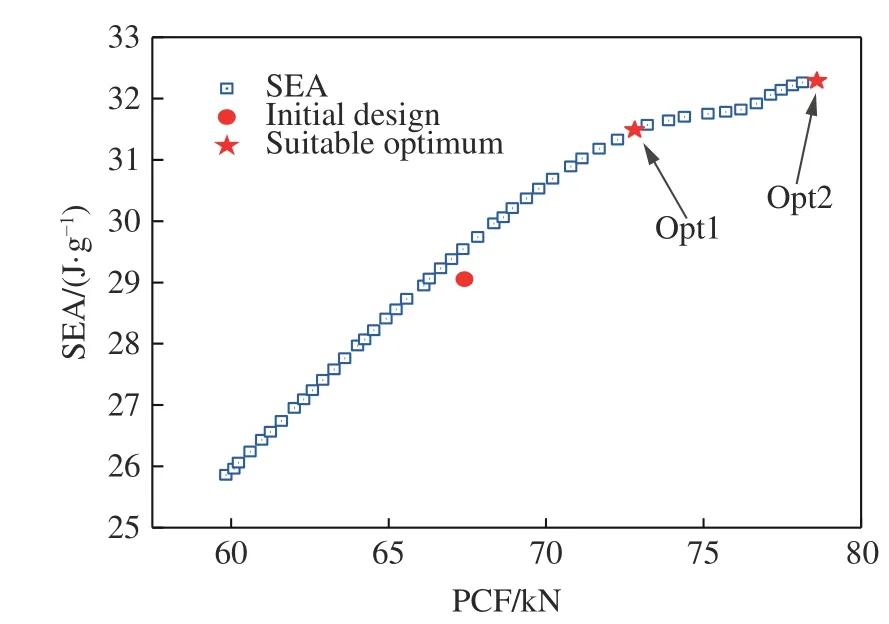
图12 薄壁结构的 Pareto 前沿Fig. 12 Pareto fronts of the thin-walled structures

表3 优化结果与有限元模拟结果比较Table 3 Comparison of the optimal results and finite element simulation
Opt2 对应的薄壁结构在压缩过程中的力-位移曲线以及变形模式如图13 所示。在压缩过程中,MCF 始终保持较大值,出现PCF 之后压缩载荷急剧下降的程度较弱,起到较好的防护作用。从变形模式和压缩力波动区间可以看出,Opt2 对应的薄壁结构在压缩过程中可以稳定吸收能量,不会出现局部欧拉变形,从而为设计吸能性能良好的薄壁结构提供参考。
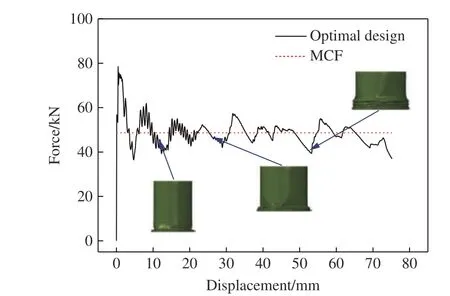
图13 Opt2 的力-位移曲线和变形模式Fig. 13 Force-displacement curve and deformation mode of Opt2
5 结 论
提出了一种新型马尾草仿生薄壁结构,探讨了其在轴向压缩下的耐撞性,通过有限元模拟分析了壁厚、内半径和连接肋对耐撞性的影响,并采用多目标优化方法进行参数优化,得到如下结论。
(1) 由于连接肋与内外圆管之间的相互作用,带倾斜肋的双圆柱薄壁管的能量吸收能力高于传统双圆管。在质量相同的条件下,SEA 提高34.74%,PCF 降低1.66%,CFE 提高了37.50%。
(2) 内半径和整体壁厚对薄壁结构的耐撞性有显著的影响,增大壁厚会增强结构刚度,在增大PCF 的同时提高结构的承载能力。当壁厚为1.20 mm 时,内半径为30 mm 的薄壁结构的SEA 最大。
(3) 在质量相同的条件下,当连接肋数目为4 时,SEA 最大,PCF 最小。SEA 和PCF 均随肋厚的增加而单调增大;不改变肋厚时,调节肋角可以降低PCF。
(4) 与最初的设计相比,优化后的薄壁结构的SEA 增加了13.42%,PCF 增加了16.43%。此时,薄壁结构参数为:内半径14.68 mm,肋角10.10°,肋的厚度1.20 mm。
