基于ESO-UKF 的动力电池内部温度在线估计*

史永胜，左玉洁，符 政，刘博亲，王 凡，JAMSHER Ali

(陕西科技大学电气与控制工程学院，陕西 西安 710021)

动力电池作为新一代大容量的绿色电源，由于其具备循环寿命长、重量轻、能量密度高[1]、无污染等突出优势，被广泛应用于各种领域[2]。动力电池的温度对其性能影响很大，当温度过低时，电池的容量将发生不可逆的损失；当温度过高时，电池内部活性物质消耗加快，加速电池老化。并且电池的内部温度很难在实际应用过程中测量得到，过高的电池内部温度会引发自燃爆炸等安全问题，因此动力电池内部温度的监测是当前研究的重点，也是保证动力电池安全运行的核心与关键[3]。

目前针对动力电池内部温度估计的研究思路有三种，第一种是利用电池内部温度与电化学阻抗谱的对应关系进行估计[4]，由于电化学阻抗谱测试系统的复杂性和成本使得该方法不适用于车载在线应用。第二种是利用有限元分析方法，应用仿真软件计算得到电池内部温度估计值[5]，离线的有限元软件不能对实时在线工况进行模拟，导致仿真结果适用性较差，所以该方法不适合于在线应用。第三种是利用电池温度估计模型估算电池内部温度[6－8]，其中文献[9]采用热路模型作为电池的热模型，利用双扩展卡尔曼滤波建立电池内部温度和环境参数的实时估计模型，实现了电池内部温度在线估计，文献[10]建立了动力电池电热模型，该模型由双态热模型和二阶RC 等效电路模型组成，考虑电池表面与环境介质之间的传热条件变化，提出了一种基于联合卡尔曼滤波的自适应内部温度估计算法。该方法计算复杂度低且适用于车载在线应用，对电池温度估计模型的精度要求较高。

本文通过试验获取电池的熵热系数与开路电压，利用神经网络得到端电压，建立准确的生热模型，与简化后的热路模型结合，建立电池温度估计模型；利用含扩展状态观测器(Extended State Observer，ESO)的无迹卡尔曼滤波(Unscented Kalman Filter，UKF)算法来估计电池内部温度；采用电池内置温度传感器在放电状态下搭建实验平台对电池进行温度测量与算法验证。

1 动力电池内部温度获取实验设计

本文以广泛应用的30 Ah INR 18650－30Q 动力电池作为研究对象，正极和负极分别为石墨和镍钴铝(NCA)，该电池具体参数如表1 所示。

表1 电池规格参数

为采集到动力电池的内部温度与表面温度值，首先将动力电池放电到截止电压，对电池负极进行钻孔后，用环氧树脂胶对钻孔进行封闭，防止电解液泄露。电池放在恒温箱中保持环境温度与散热条件稳定。具体实验平台如图1 所示。由于动力电池在放电时内部温度变化较为明显[11]，实验安排如下。

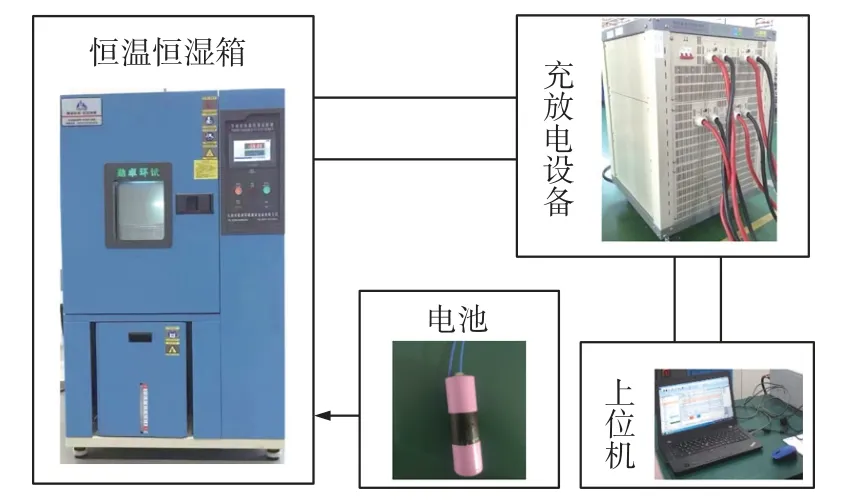
图1 实验平台

(1)在每次放电实验前都将动力电池放置在25 ℃恒温箱中，以传统充电方式先恒流再恒压充电直至充满，并静置一小段时间，消除电池内部极化效应与浓差效应的影响；

(2)对电池进行连续变化电流的放电，该放电电流如图2 所示；

(3)分别采用2C、5C 对电池恒流放电，直至完全放电；

(4)记录以上电池放电过程中的电池内部与表面温度。

基于上述实验平台共开展了3 组放电下的内外温度测量试验，即图2 中连续变化电流的放电、2C下的恒流放电、5C 下的恒流放电。

图2 连续变化的放电电流工况

2 电池温度估计模型

2.1 热路模型

建立准确的传热模型是实现动力电池内部温度估计的关键，文献[9]提出的热路模型计算量小且精度高，热路模型基于传热学和电路理论为传热过程建立等效热模型。建立等效热路模型前基于以下假设:(1)电池的热量是从电池内部均匀产生的；(2)沿轴向电池的温度均匀分布；(3)电池生热量仅通过电池径向方向向外传递[12]。

如图3 为动力电池热路模型示意图，基于热路模型理论，分别使用电容和电阻描述热路模型中的热容和热阻；将热源视为电路中的直流源；而温度则等效为该点处的电势。由此，结合电路模型的基尔霍夫定律，推导得到动力电池的热路模型的求解方程，并得到该热路模型的方程式如下:

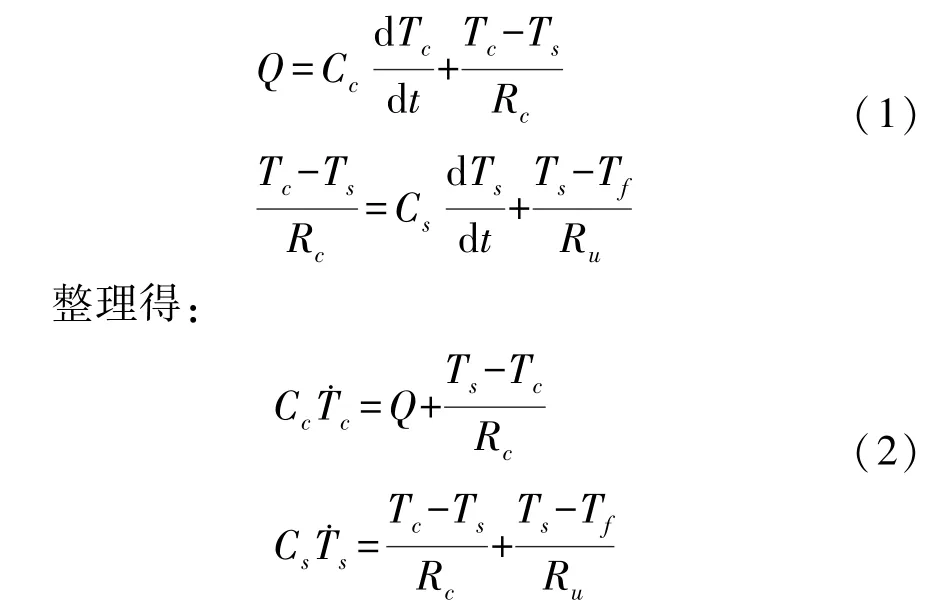
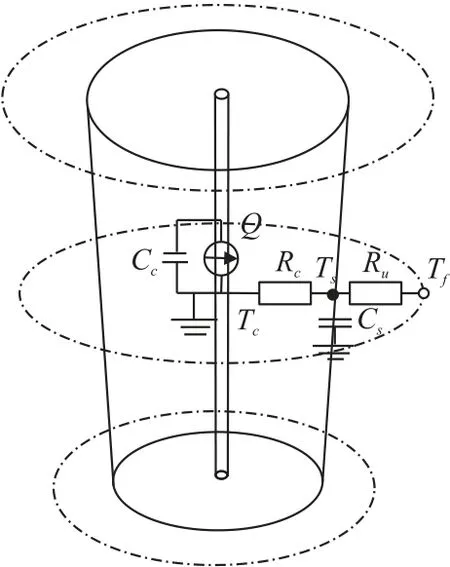
图3 动力电池热路模型示意图

式中:Ts和Tc分别代表电池表面温度和电池内部温度；Tf为环境温度；Cc和Cs分别表示电池内部集中热容和电池表面集中热容；Rc为等效热传导电阻，用于模拟电池内部和电池表面之间的热交换；Ru为等效热对流电阻，用于模拟电池表面的对流冷却；Q表示电池工作期间的产热。

2.2 生热模型

准确计算电池的生热是估计电池内部温度的基础，目前动力电池的生热一般采用Bernardi 生热模型[13]计算。

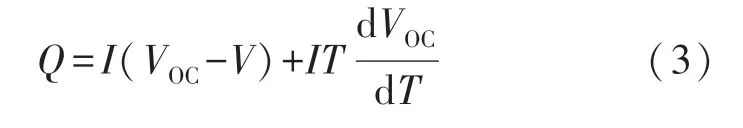
式中:I为电池的充放电电流，V为电池端电压，VOC为电池的开路电压，T为电池的温度，代表熵热系数。该公式第一部分为不可逆热，形成的原因是电极极化。第二部分为可逆热，主要是由熵热引起的[14]。

电池的温度T为电池的平均温度即:

运用安时积分法将动力电池的荷电状态(State of Charge，SOC)定义为:

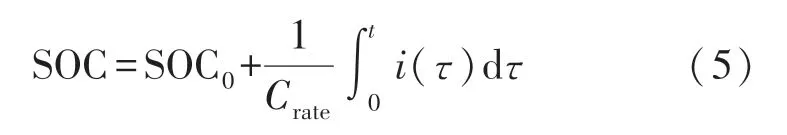
式中:SOC0为动力电池初始的SOC 值；Crate表示动力电池的额定容量。

电池的VOC可以通过VOC与SOC 的非线性关系得到，为了得到这一非线性函数对电池进行混合脉冲功率测试(hybrid pulse power characteristic，HPPC)[15]，得到VOC随SOC 变化的曲线图如图4 所示。

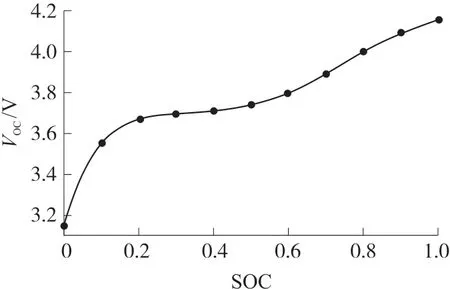
图4 VOC-SOC

在现有的研究中计算电池的不可逆热时端电压常常直接由传感器测量得到[6]，但在实际测量中动力电池的端电压变化幅度剧烈难以测量，且其本身是电流、SOC、电池温度的函数，因此为了获得准确的不可逆热必须建立一个准确的端电压预测模型使其能够适应负载电流和运行条件的变化[16]。神经网络中的隐层结构加上神经元里的非线性激活函数，可使得神经网络随意逼近任意函数，适合处理电池端电压与温度、SOC 和电流之间的非线性关系。所以将电流、SOC、电池温度作为神经网络的输入，电池的端电压作为神经网络的输出，并在基本神经网络结构上加入Levenberg-Marquart 算法[17]进行优化，Levenberg-Marquart 算法是高斯－牛顿法与梯度下降法的结合，通过控制算法中的阻尼因子λ(λ小时，步长等于高斯－牛顿法步长；λ 大时，步长等于梯度下降法计算的最优步长)，调节寻优步长，实现快速收敛。如图5 为利用神经网络得到的电池端电压的估计结果与估计误差，由估计结果可以看出，实测动力电池端电压与神经网络模型输出端电压大致相同，误差≦0.02 V，所以该模型可以得到准确的端电压值。

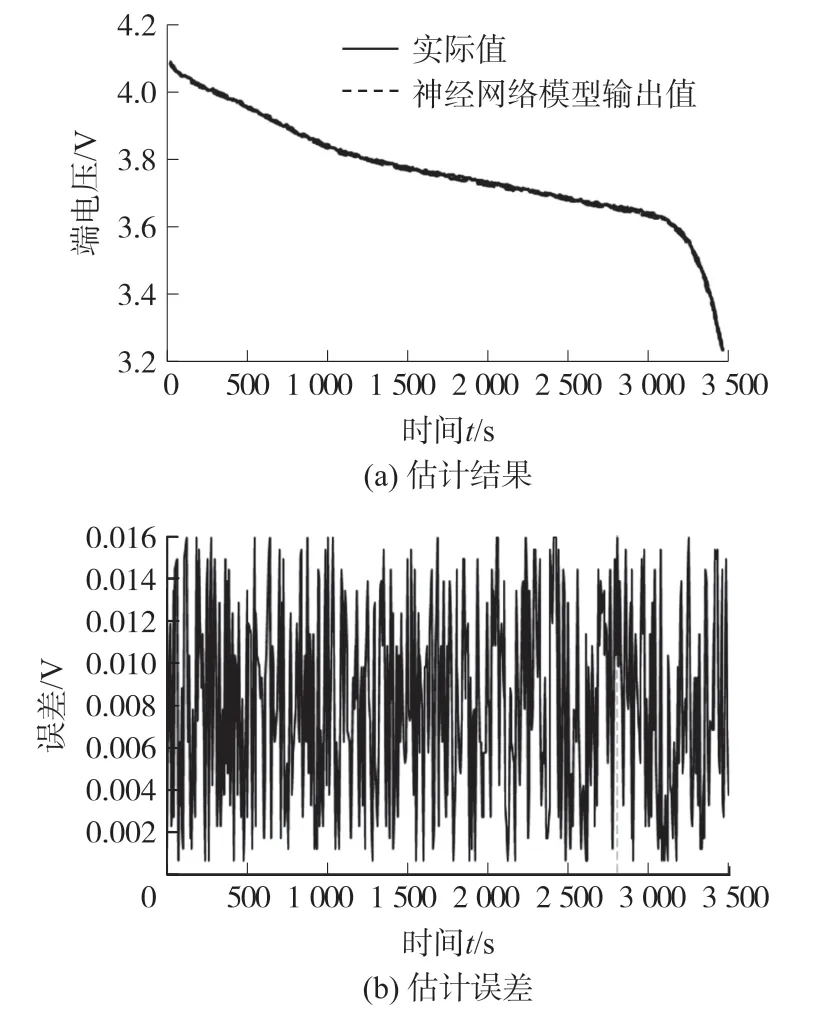
图5 电池端电压的估计结果与估计误差

动力电池的熵热系数又称开路电压温度系数，是一个仅与SOC 相关的量，其数值几乎不受温度影响。该值可通过实验测得，即在特定的温度与特定的SOC 条件下，测得电池的开路电压的变化值。如图6 为最终获取的熵热系数与SOC 的关系图。

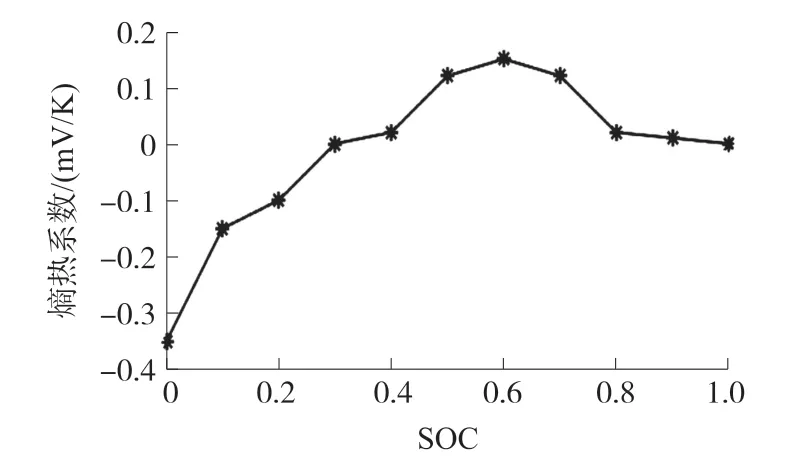
图6 电池熵热系数-SOC 曲线

2.3 动力电池热路模型参数辨识

准确的模型参数值是估计算法准确性的基础。热路模型需要辨识的参数有Cc、Cs、Rc与Ru。应用动力电池工作中的实际测量值与模型输出值不断更正模型参数，可以实现模型的在线辨识。对于电池模型参数求解采用递推最小二乘法(RLS)[18]，由电池生热模型求得的Q作为输入，递推最小二乘法的计算公式如下:

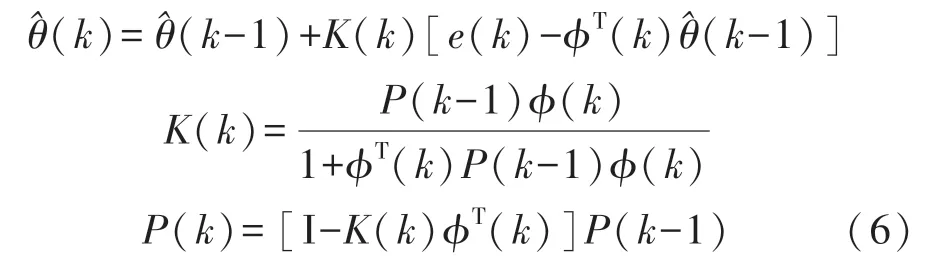
式中:为电池模型所求参数向量输出；φ为实验数据矩阵；K为增益；P为协方差矩阵，e(k)为测量输出，I 为单位矩阵。递推最小二乘法对动力电池热路模型进行参数辨识，计算过程如图7 所示。

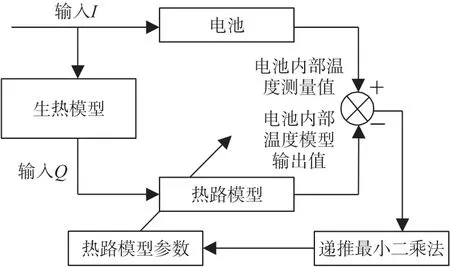
图7 热路模型参数辨识

热路模型参数的最终辨识结果见表2。

表2 热路模型参数辨识结果

2.4 电池温度估计模型验证

采用如图2 所示连续电流放电工况对动力电池温度估计模型的精度进行验证，电池模型估计结果输出如图8(a)所示，误差如图8(b)所示，结果表明模型的温度估计误差在±1.5 ℃之间，验证了所建立的温度估计模型的精度。

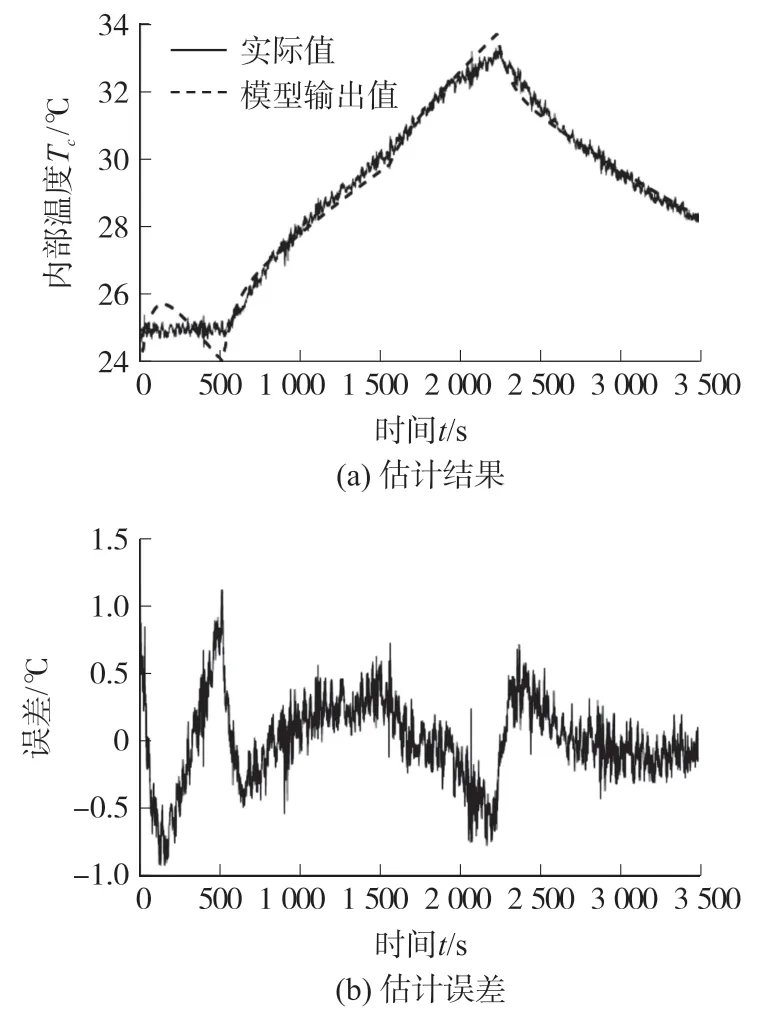
图8 电池温度估计模型的估计结果与估计误差

3 基于ESO-UKF 的电池内部温度估计方法

由于所建立的温度估计模型进行参数辨识和验证模型准确性时，需要在电池钻孔的条件下得到动力电池的内部温度，但是在实际工况中，动力电池的表面温度可以用热传感器或热电偶直接测量，电池的内部温度很难直接测量得到，所以通过其他可测量信号进行内部温度的测量非常重要。

3.1 UKF 理论

无迹卡尔曼滤波算法(Unscented Kalman Filter，UKF)最早是由Julier S 等人[19－20]提出的一种非线性滤波方法，利用UT 变换(unscented transform，UT)选取一组sigma 点来匹配该非线性系统的统计特性进行非线性模型的状态和误差协方差的递推更新，不需要对非线性系统线性化，这样就避免了误差，并且在计算时仅涉及向量和矩阵运算，计算复杂度低。

非线性离散动态系统可以表示为:

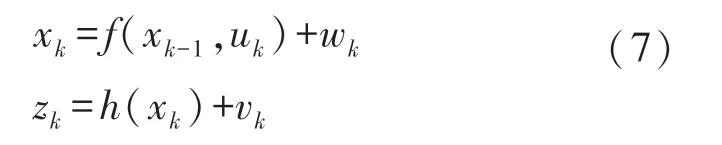
式中:xk是第k步的状态向量，zk是观测向量；f和h分别代表非线性系统状态转移方程和非线性系统观测方程；wk和vk分别代表过程噪声和测量噪声，都为高斯白噪声，且其协方差矩阵分别为:

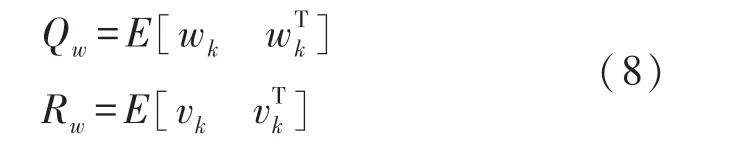
则UKF 算法的算法流程如下:

(1)设置初始条件:

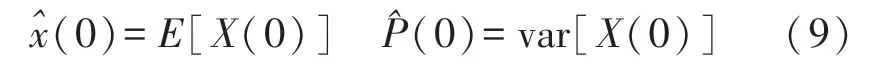
(2)sigma 点取样:

具有相关权重的一组样本点如下:

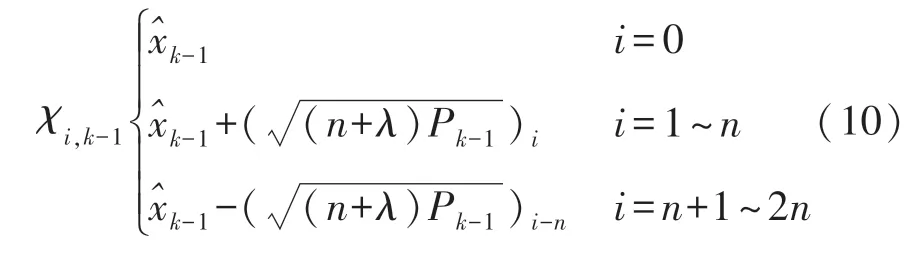
确定加权系数

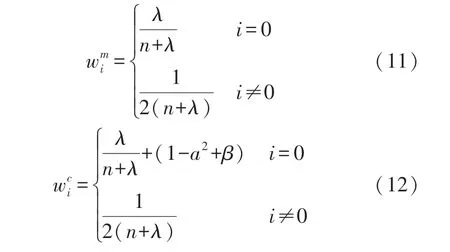
(3)时间更新

通过sigma 样本点，计算均值和协方差:

(4)测量更新

K时刻的状态变量和它的误差协方差Pk可根据以下方式更新，其中Kk为卡尔曼增益。

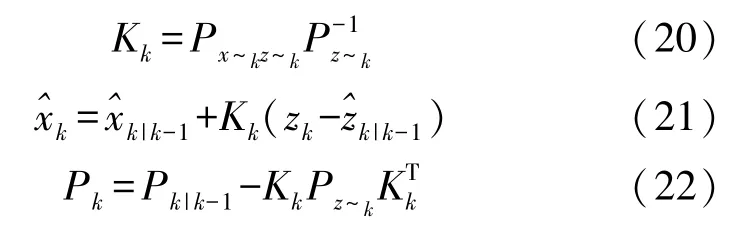
(5)随着时刻推移，递推重复上述流程，可以得到每一时刻系统最优状态变量估计值与误差协方差估计值。

3.2 ESO-UKF 算法

为了将UKF 应用于电池温度估计，将热模型的表达式转换为状态空间，并将连续常微分方程模型离散如下:

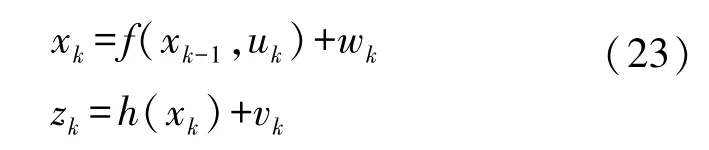
式中:xk是由内部温度x1和表面温度x2组成的状态向量，输入uk为电池生热模型计算得到的生热量Q，zk是表面温度的观测值，加上vk、wk用于表示一些随机未建模动态。图9 为针对动力电池在图2 连续变化的电流工况下放电所得到的实验数据，以动力电池的表面温度作为UKF 算法的观测量进行内部温度的估计的结果。但在实际工况中，当算法的观测量，如电池表面温度的测量因电磁干扰、传感器老化、接触不良等原因造成偏差时，算法估计精度会显著变差。

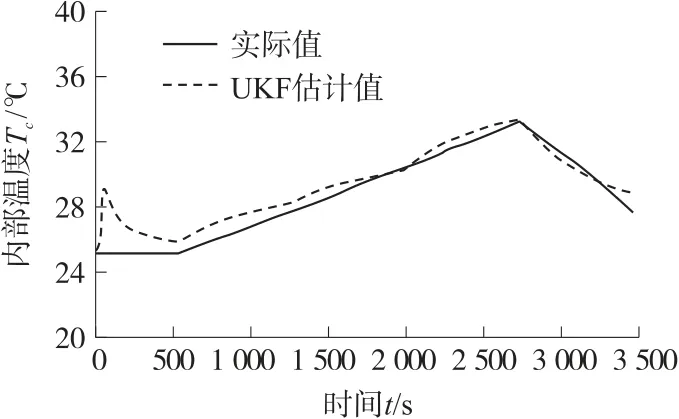
图9 连续放电电流下基于UKF 的估计结果

为此，本文采用了扩展状态观测器(ESO)的思想，扩展观测器是由韩京清在上世纪90 年代提出[21]。ESO 是用来估计系统中的“总扰动”，包括未建模的状态与外部扰动。将被控系统中的所有不确定性和干扰扩展为新的状态，并通过ESO 进行估计，ESO 的扩展状态变量为影响控制性能的干扰项，通过将扩展状态变量反馈至系统输入端以抵消干扰影响。所以将考虑表面温度中存在的传感器测量偏差，该偏差通过在表面温度的测量值中人为添加常数值实现，传感器偏差被扩展为新状态x3，将原始模型修改为增强形式:

因此，由以上手段现有传感器偏差的信息被结合到系统模型中，基于增强模型，得到ESO-UKF 算法。

4 仿真与结果分析

针对动力电池在如图2 连续变化的电流下放电，2C 恒流、5C 恒流下放电所得到的试验数据，应用ESO-UKF 算法与传统UKF 算法进行电池内部温度估计，所得到的各个工况下的试验结果与仿真估计结果如图10～图15 所示。参考如图所得的试验结果，动力电池在放电过程中存在较大的温升，其中在连续变化电流的放电与2C 恒流放电过程中动力电池内部最大的温升在10 ℃左右，而在动力电池的最大允许电流5C 下放电时，其内部最大温升高达40 ℃，由此可见对动力电池进行内部温度估计的重要性。并且在考虑了传感器偏差后ESO-UKF 算法对连续电流放电与恒流放电工况均具有良好的适应性，其估计结果与实际值相符。

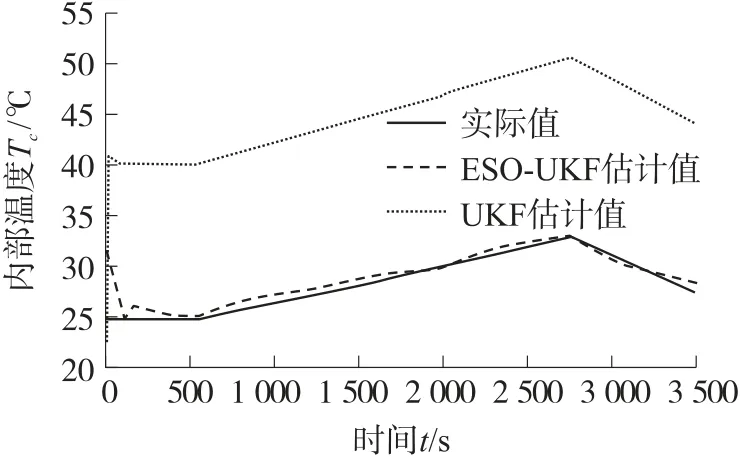
图10 连续放电电流下的估计结果

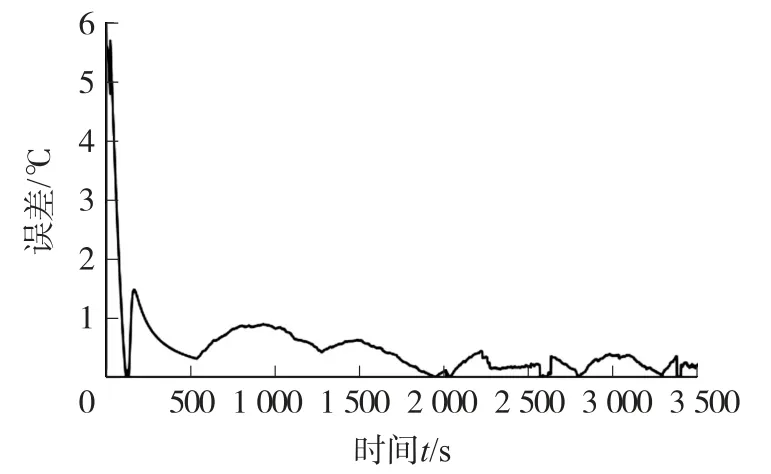
图11 连续放电电流下ESO-UKF 估计误差的绝对值

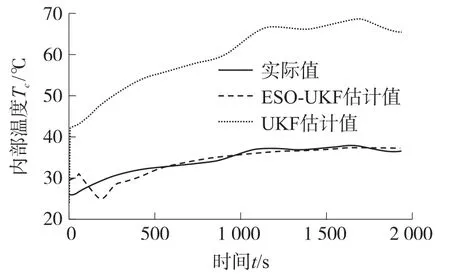
图12 2C 放电电流下的估计结果

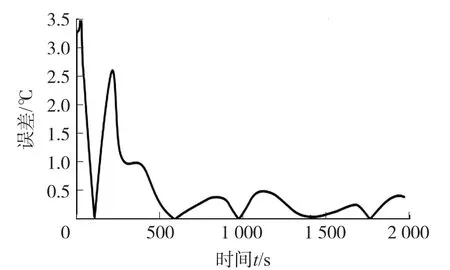
图13 2C 放电电流下ESO-UKF 估计误差的绝对值

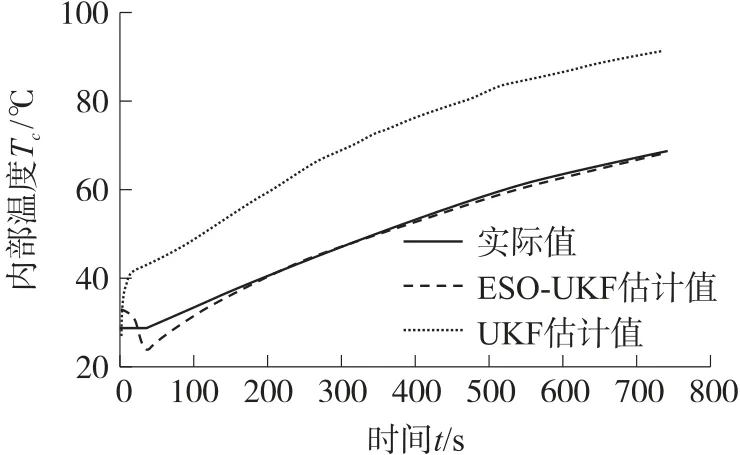
图14 5C 放电电流下的估计结果

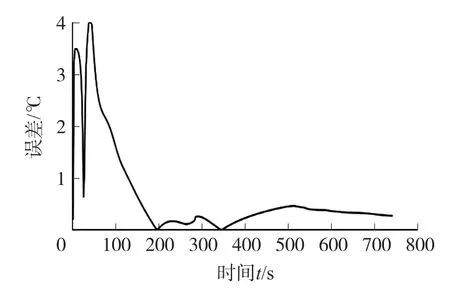
图15 5C 放电电流下ESO-UKF 估计误差的绝对值

但是传统的UKF 算法无法估计动力电池的内部温度，图10、图12、图14 分别在连续变化的电流下放电，2C、5C 恒流下放电工况下，UKF 算法的内部温度估计值比真实的内部温度估计值大约高20 ℃～40 ℃。这是因为当考虑表面温度的传感器偏差后，传统UKF 算法错误地将带有偏置的表面温度值作为算法的观测量，从而造成较差的估计结果。而ESOUKF 算法将估计过程中的不确定性的状态进行扩展处理，将实际测量中可能出现的传感器偏差结合在系统模型中对电池内部温度进行估计，提高了算法的精度，实现了动力电池内部温度的软测量。

由图11、图13、图15 可知，由于在每次的放电试验前都将动力电池放置在恒温箱中静置一小段时间，在该静置时间内无产热量输入，此时电池的内部温度为恒温箱所设置的环境温度，所以此时ESO-UKF 算法在内部温度估算初期的估计结果误差较大，但经过卡尔曼滤波算法的迭代最终在静置结束趋于稳定后估计误差的绝对值均小于1 ℃，即估计结果趋于真实值。这是因为ESO-UKF 算法在线估计时在表面温度测量值中加入了10 A 的传感器偏差，此时算法观测量初始值的设定与原真实数据存在极大的偏差，但随着ESO-UKF 算法在进入测量更新和时间更新的迭代过程后，随着迭代次数的增加算法估计的误差越来越小并逼近真实的结果，这表明ESO-UKF 算法在进入测量更新和时间更新的迭代的过程中初始值的设定对算法的估计精度不会造成影响。

5 结论

针对动力电池内部温度难以直接获取的问题，利用Bernardi 生热模型与热路传热模型结合建立温度估计模型，进行参数辨识，模型的精度高，误差在±1.5 ℃之间。基于所建立的模型利用ESO-UKF 与UKF 两种算法估算电池内部温度，ESO-UKF 算法能够准确估计动力电池的内部温度，在不同的工况下稳定后的估计误差均小于1 ℃，实用性强，实现了动力电池内部温度的软测量。ESO-UKF 将估计过程中的不确定性的状态进行扩展处理，提高了算法的精度，实现了动力电池内部温度的精确估计，该内部温度估计方法为电池的安全管理以及车载应用等提供了理论支撑。