基于正割补偿的天线高仰角跟踪动态滞后性研究

高 菲，张 卓，梁 敏，吴宗清，王 涛，宋微微

(1.宇航动力学国家重点实验室，陕西 西安710043;2.中国西安卫星测控中心，陕西 西安 710043)

0 引言

方位—俯仰型天线座架系统在航天测控和卫星通信等相关工程领域有着广泛应用，但这种座架天线受方位驱动能力的限制，在天顶附近存在一定的跟踪盲区，导致不能连续跟踪目标，影响了对目标的跟踪控制与数据接收[1-2]。工程应用上可采用三轴倾斜机械过顶[3-4]，但三轴天线对结构的要求较高，一般适用于小型口径天线，大多数方位—俯仰型天线采用程控引导方式或数字引导方式完成过顶跟踪[5-7]。程控引导方式过顶需要依靠完整的理论弹道，当目标接近跟踪盲区时，天线提前加速冲出盲区后再转入对目标的跟踪捕获，必然造成一段时间的目标丢失，目标丢失时间可计算。数字引导是由测控中心利用地面测控设备外测数据和航天器GNSS数据等实时综合计算目标位置，测控设备据此解算天线指向位置，与理论弹道相比准确率更高，过顶时天线按照最大动态性能进行目标跟踪，可最大程度减少目标丢失时间，所以航天器发射段高仰角过顶跟踪一般采用数字引导方式完成[8-9]。在此方式下，若天线方位最大速度仍小于航天器飞行速度，天线仍会出现不同程度的动态滞后。

目前，国内对方位—俯仰型天线动态滞后研究主要是利用正割补偿对天线仰角进行坐标转换以提高天线的过顶跟踪性能[10-13]，但对航天器发射段天线采用数字引导跟踪时出现的动态滞后分析研究不多，在工程应用分析中也仅考虑天线波束宽度的制约，未考虑天线在空间中的实际跟踪情况。

本文利用正割补偿原理，从天线跟踪的实际空间角度出发，分析测控设备采用数字引导方式高仰角过顶跟踪时天线的动态滞后性。测控中心能够根据本文方法计算出波束偏离目标的准确时间，从而避免在此时段上注指令。

1 正割补偿原理

航天测控设备以大地水平面为坐标系基准对目标进行跟踪和测量，正割补偿原理如图1所示。

图1 正割补偿原理Fig.1 Principle of secant compensation

目标从B点以速度V向C点运动，此时天线指向为OB。天线接收机测出的角误差信息为θx，即∠BOC。天线跟踪目标从OB转到OC，需要通过方位和俯仰2个轴的转动来实现，在方位平面上(大地水平面)从OA转到OD，要转过一个方位角θ，在俯仰平面上俯仰角从∠BOA转到∠COD要转过一个角度ε。只有在俯仰角ε为零时，θx才能等于方位角θ[14-16]，但在实际跟踪过程中，俯仰角ε通常不等于0。

θx与θ之间的关系为[17-18]：

sinθ=AD/OD，

(1)

cosε=OD/OC，

(2)

sinθx=BC/OC。

(3)

由式(3)可得：

BC=OCsinθx，

(4)

sinθ=(OCsinθx)/OD，

(5)

OD=OCcosε，

(6)

所以，

sinθ=(OCsinθx)/(OCcosε)=sinθxsecε。

(7)

当θ很小时，θx也很小，有：

θ=θxsecε，

(8)

则：

θx=θcosε。

(9)

2 天线高仰角跟踪动态滞后性分析方法

2.1 动态滞后现象分析

航天测控系统中，影响目标跟踪性能的一个主要因素为天线的动态滞后问题。当目标运行至测站过顶前后，其方位角上的变化加剧。由于伺服系统在设计时，其影响跟踪的角度滤波算法，一方面受系统环路时延影响，另一方面受硬件转台的能力影响，其角跟踪存在一定的动态滞后。在仰角较低时，动态滞后并不明显；在过顶附近，由于方位角的变化加剧，方位角的动态滞后问题更加突出。当方位上的滞后角度ΔA大于波束宽度θλ的一半时，会导致目标偏离出天线波束主瓣。

为保证对目标测控任务的正常执行，一方面需要提高跟踪精度，即减小动态滞后的影响，尤其是目标处于高仰角时的动态滞后；另一方面需要及时通过数字引导的方式引导波束指向，使目标始终处于波束主瓣范围内。

2.2 基于正割补偿的滞后角度与时间计算方法

天线跟踪空中目标时，由于测量的方位角和实际空间中的方位角存在一个转角增量，需要通过正割补偿的方式进行修正。在高仰角跟踪的过程中，若不进行补偿，会由于方位角度变化过大导致动态滞后严重，从而影响目标跟踪性能。

设天线波束宽度为θλ，天线方位最大性能为vmax，天线跟踪过程中实时测得的方位角度为A，俯仰角度为E，数字引导计算出的飞行器方位预报角度为Ay，飞行器偏离天线波束的方位角度差为βA，飞行器在实际空间中偏离天线的横向角度为β，则：

βA=Ay-A。

(10)

考虑跟踪过程中俯仰角的影响，根据式(9)，飞行器在空间中实际偏离天线的横向角度为：

β=βAsec(E·π/180)。

(11)

由式(10)可得：

β=(Ay-A)sec(E·π/180)。

(12)

当β>θλ/2时，目标已经偏离天线波束主瓣，此时方位角度为βa；当β<θλ/2时，目标处于天线主瓣范围内，此时方位角度为βb，则目标丢失时间T为：

T=(βa-βb)/vmax。

(13)

因此，在天线跟踪过程中，跟踪算法需要采用正割补偿后的目标偏离天线的方位角度，从而减小高仰角跟踪时在方位角上动态滞后过大的影响，提高跟踪精度。

3 应用实例分析

以10 m口径测控设备为例，天线波束宽度为0.95°，方位最大速度性能20 (°)/s，方位最大加速度性能20 (°)/s2。给定高仰角的目标飞行弹道过顶最大仰角87°，过顶前后飞行器方位最大速度53 (°)/s、最大加速度28 (°)/s2。根据指标分析，目标飞行器过顶最大速度和加速度已经远远超过测控设备天线方位动态指标，设备无法满足对目标飞行器的自跟踪要求，需采用数字引导方式跟踪过顶。

通过提前加载目标飞行器理论弹道，对天线在数字引导方式下随动的存盘数据进行过顶动态滞后性的理论分析。目标飞行器的理论弹道按照每秒一点的命令角位置实时发送给设备，则飞行器的实时方位角度值即为数字引导预报的方位角度值。

本节按照不考虑俯仰角影响和考虑俯仰角影响进行数据分析，最后将2种理论分析结果与发射段天线高仰角过顶实际跟踪情况进行比对，验证对天线过顶动态滞后性理论分析的准确性。

3.1 不考虑空间俯仰角影响的动态滞后性分析

加载飞行器理论弹道后，天线数字引导随动的存盘数据动态滞后性分析如图2所示。蓝色曲线为数字引导预报的方位角度，即目标飞行器的理论弹道。红色曲线为天线当前的方位角度。绿色曲线为天线当前的俯仰角度。

图2 不考虑空间俯仰角影响天线方位角度滞后分析Fig.2 Analysis of antenna azimuth hysteresis without considering spatial elevation

由图2可以看出，不考虑空间俯仰角影响，天线仰角在80.2°时，天线方位角度已经开始滞后于数字引导预报的目标方位角度。此时方位角差值为0.506°，已经大于天线半波束宽度，目标已经偏离天线波束主瓣。直到目标过顶，目标速度达到最大52.5 (°)/s，此时天线仍按最大速度20 (°)/s追赶目标，导致天线方位严重滞后，过顶方位最大差值达到56°，如图3所示。天线仰角为78.2°时，天线实时方位角度已经和数字引导预报的目标飞行器方位角度重合，此时方位角差值为0.424°，目标重新进入天线波束主瓣，设备可重新捕获目标。天线过顶期间，在航时540 s时目标出波束，航时550 s时目标重新进入天线波束，跟踪期间共丢失目标10 s。

图3 不考虑空间俯仰角影响天线与目标最大方位角偏差Fig.3 Maximum azimuth deviation between antenna and target without considering spatial elevation

3.2 考虑空间俯仰角影响的动态滞后性分析

考虑空间俯仰角影响天线方位角度滞后分析如图4所示。蓝色曲线为数字引导预报的方位角度，即目标飞行器的理论弹道。红色曲线为考虑空间俯仰角影响，利用正割补偿原理将天线当前的方位角度折算为空间中的方位横向角度。绿色曲线为天线当前的俯仰角度。

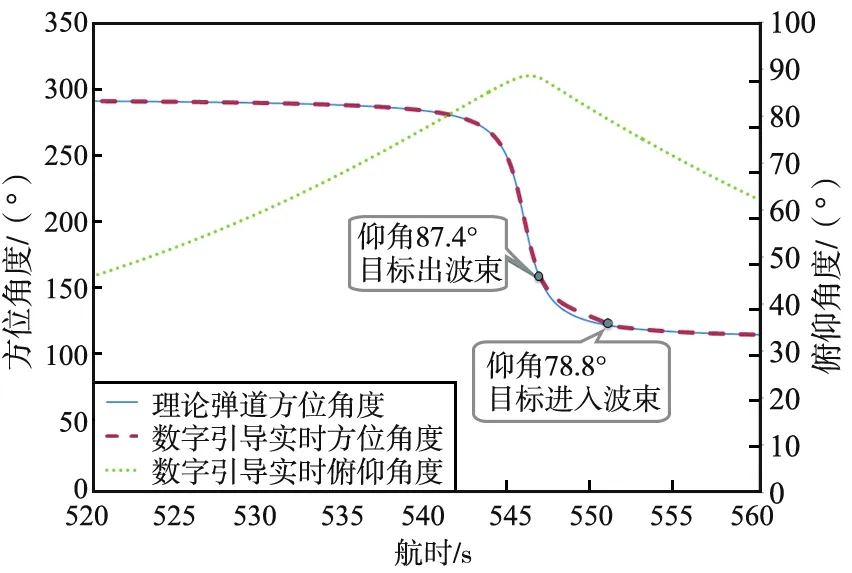
图4 考虑空间俯仰角影响天线方位角度滞后分析Fig.4 Analysis of antenna azimuth hysteresis considering spatial elevation

由图4可以看出，天线仰角为87.4°时，天线实时方位角度开始滞后于数字引导预报的目标飞行器方位角度，此时方位角差值已经大于天线半波束宽度，目标已经偏离波束主瓣。直到目标过顶，天线速度达到最大52.5 (°)/s，此时天线仍按最大速度20 (°)/s追赶目标，导致天线方位严重滞后，考虑到俯仰角影响，经过正割补偿后在实际空间中天线与目标的方位角度差仅为4.6°，如图5所示。由图5可以看出，天线仰角为78.8°时，天线实时方位角度已经和数字引导预报的目标飞行器方位角度重合，此时方位角差值已经小于天线半波束宽度，目标重新进入天线波束主瓣，设备可重新捕获目标。天线过顶期间，在航时545 s时目标出波束，航时550 s时目标重新进入天线波束，跟踪期间共丢失目标5 s。

图5 考虑空间俯仰角影响天线与目标最大方位角偏差Fig.5 Maximum azimuth deviation between antenna and target considering spatial elevation

3.3 工程验证结果

对飞行器理论弹道和发射段实际弹道进行比较，弹道一致，如图6所示。在此基础上，根据实际跟踪情况验证动态滞后性理论分析的准确性。

天线方位角度滞后实际跟踪情况如图7所示。图中红色曲线为天线在实际跟踪过程中的实时俯仰角度，蓝色曲线为跟踪过程中基带接收的下行信号AGC电压。如果目标在天线主瓣，天线能够稳定跟踪，AGC维持在4 V左右(绿色曲线)。如果目标开始偏离天线主瓣，AGC电压整体会出现下降趋势，在偏离过程中，目标逐渐远离主波束，会依次经过天线各旁瓣，导致AGC电压有一定起伏，下降到1 V以下，信号将失锁。

由图7可以看出，当天线仰角到87.7°时，AGC电压开始下降，表明此时目标开始偏离波束主瓣。目标过顶时，AGC电压已下降到接近1 V，此时天线已经出现动态滞后，实时方位角度与数字引导预报方位角度(即目标飞行器方位)差值达到4.7°。天线仰角为78.6°时，AGC电压已经升至接近4 V，目标重新进入天线主波束。

(a) 理论弹道

(b) 实际弹道图6 飞行器理论弹道和实际弹道比较Fig.6 Comparison between theoretical and actual trajectories of air vehicle

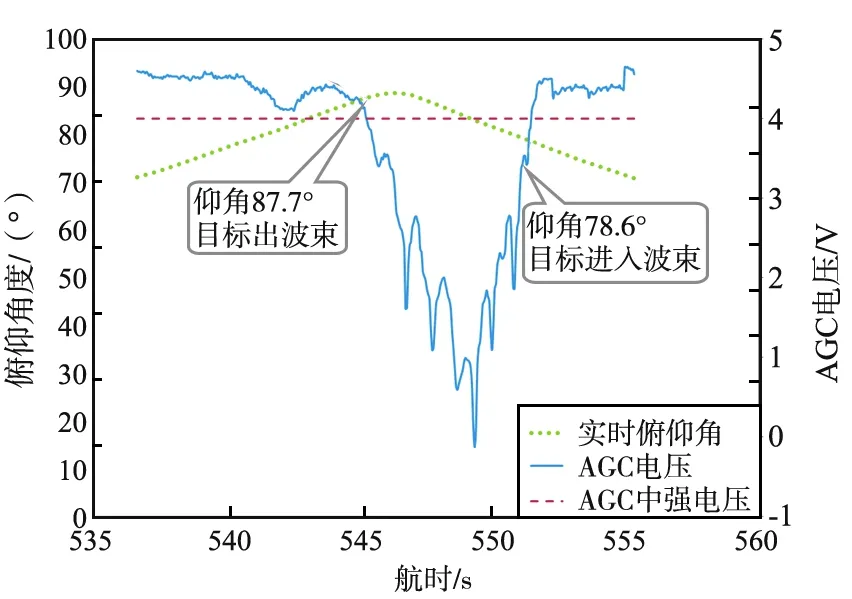
图7 天线方位角度滞后实际跟踪情况Fig.7 Antenna azimuth hysteresis in actual tracking

实际跟踪中的天线方位角度与飞行器方位角度差值如图8所示，可以看出，天线过顶期间，在航时545 s时目标出波束，航时551 s时目标重新进入天线波束，跟踪期间共丢失目标6 s。

图8 实际跟踪中的天线方位角度与飞行器方位角度差值Fig.8 Difference between antenna azimuth and air vehicle azimuth in actual tracking

分析结果比较如表1所示。由表1可以看出，正割补偿分析方法下的目标偏离天线波束仰角、目标重新进入天线波束仰角、动态滞后方位角度差值以及动态滞后时间等指标参数均更加趋近于实际跟踪结果。

表1 分析结果比较

4 结束语

在数字引导方式下天线高仰角过顶跟踪，若方位最大动态性能小于目标飞行速度，天线会出现不同程度的动态滞后，影响测控设备的稳定跟踪。本文充分考虑空间俯仰角影响，提出了一种基于正割补偿原理的测控设备高仰角过顶跟踪航天器动态滞后性的理论分析方法。通过与天线实际跟踪数据比较，该方法准确性高，能够为制定发射段天线捕获和跟踪策略提供理论支撑，为测控中心上注指令时间的安排提供依据。