非视距环境下的IMU和UWB融合定位系统

彭俊杰，李英华，王春琦，周小安

(1.深圳大学 电子与信息工程学院，广东 深圳 518060；2.国家无线电监测中心，北京 102609)

0 引言

自组织网络系统内没有中央控制实体，节点之间可以直接共享资源和服务，具有完全的自主性和平等的地位，使得自组织网络具有灵活、无中心、自组织、可扩展性强、负载平衡和很好的抗毁性等特点，越来越受到学术界和工业界的关注。自组织的对等计算模式已给计算机和通信网络领域带来了重大的变革，在文件共享、内容分发、协同计算和即时通信等方面，以及军事、传感器网络、紧急场合、动态临时场合和商业上都有广泛的应用。随着物联网技术的不断发展，基于位置的服务(Location Based Service，LBS)越来越受到人们的重视。室外场景下的定位应用已经十分成熟，但是面对更为复杂的室内环境，室外定位技术不能满足人们的日常生活需求。在数字化的交互应用场景下，高精度的室内定位系统有着巨大的市场潜力。例如智慧家居、智慧园区和智慧商超的建设，都需要高精度的室内定位系统作为硬件基础。目前主流的室内定位技术包括超宽带、蓝牙、WiFi、ZigBee、红外线、LED和超声波等方式。超宽带(Ultra-Wide Band，UWB)相较于其他传感器具有更低的能耗和更高的定位精度，但是基于信号传输的传感器都会受到非视距(None-Line-of-Sight，NLOS)的干扰，从而影响到定位的精度[1]。UWB的通信机制主要包括基于时间、到达角度和信号强度的方式。在基于时间的测距方式中包括基于信号的到达时间(Time of Arrival，TOA)[2]、到达时间差(Time Difference of Arrival，TDOA)[3]、时分多址(Time Division Multiple Access，TDMA)和双向测距(Two-way Ranging，TWR)。其中TWR和TDOA技术的测距精度较高，也更易于实现，且对基站和标签之间的时间同步要求不高。基于到达角度的定位方式中主要包括信号到达角度(Angle of Arrival，AOA)和到达相位差(Phase Difference of Arrival，PDOA)。惯性测量单元(Inertial Measurement Unit，IMU)不受NLOS的影响，可以结合IMU的定位信息进行融合定位。

1 定位系统描述

基于自组织的分布式网络管理模型如图1所示，主要由3部分组成：网管服务器、分布式网络代理(Distributed Network Agent，DNA)和被管设备。

图1 自组织的分布式网络管理模型Fig.1 Self-organization distributed network management model

IMU传感器中的陀螺仪通过姿态矩阵进行姿态解算，加速度计通过二次积分获得位置信息。UWB通过基站与标签之间的通信解算出位置信息[4]。通过当前位置和UWB测得的距离信息采用支持向量机(Support Vector Machine，SVM)[5-6]进行NLOS信号的识别分类。卡尔曼滤波(Kalman Filter，KF)通常用于室内定位的算法融合[7-9]，也有基于KF提出的2步KF算法定位[10-11]，在视距(Line-of-Sight，LOS)场景下利用UWB基于最小二乘(Least Squares，LS)[12]算法定位，提出了采用LS和EKF融合的定位算法[13-14]。

1.1 IMU定位系统

IMU主要元件有陀螺仪、加速度计和磁力计。其中，陀螺仪可以得到各个轴的加速度，加速度计能得到x，y，z方向的加速度，而磁力计能获得周围磁场的信息。IMU器件主要的工作是将3个传感器的数据融合得到较为准确的姿态信息。陀螺仪测量角速度，通过一次积分得到角度值。加速度计测量加速度，通过一次积分得到速度。通常来说陀螺仪的温漂是比较严重的，温漂的数据既与温度相关又与时间相关，在不同的温度和上电时间的情况下，会产生不同的温漂值。

惯性导航中基于牛顿力学定律的基础，采用惯性导航坐标系。载体进行导航的过程中实时地确定其导航参数，如载体的姿态、位置和速度等。载体的导航通过各个坐标系之间的关系确定，惯性导航坐标系下解算的坐标信息需要经过坐标系转换，才能应用到实际的场景下，惯性导航坐标系的转换如图2所示。

图2 惯性导航坐标系的转换Fig.2 Transformation of inertial navigation coordinate system

图2中，ψ，θ，γ分别表示载体的航向角、俯仰角和横滚角，不同颜色的坐标轴表示每一次旋转后的坐标系状态，经过3次坐标轴的旋转就能实现从载体坐标系变换到导航坐标系。第1次绕垂直于z0轴的平面旋转ψ角，从坐标系Ox0y0z0转换到坐标系Ox1y1z0，第2次绕垂直于x1轴的平面旋转θ角，从坐标系Ox1y1z0转换到坐标系Ox1yz1，第3次绕垂直于y轴的平面旋转γ角，从坐标系Ox1yz1转换到坐标系Oxyz。通过3次旋转可以得到方向余弦矩阵：

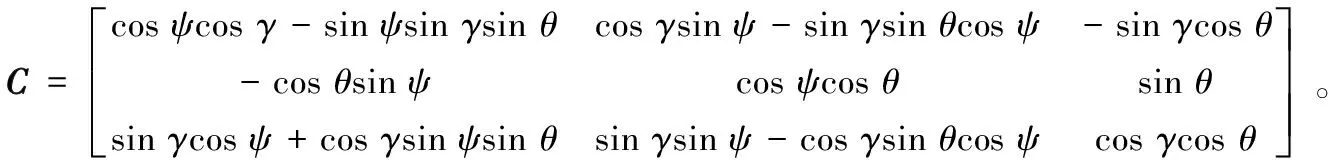
(1)

当ψ，θ，γ都比较小时，略去二阶小量，得：

(2)

式(2)即为实际定位中采取的旋转矩阵。基于旋转矩阵，可以将IMU在导航坐标系下解算的位置信息转换到地理坐标系中。

1.2 UWB定位系统

UWB是一种基于极窄脉冲无载波的无线技术，传输速率高，发射功率较低，穿透能力较强，能在短距离内高速传输数据。UWB不采用正弦载波，而是利用ns级的非正弦波窄脉冲传输数据，因此其所占的频谱范围很宽，适用于高速、近距离的无线个人通信。UWB、宽带和窄带的信号比较模型如图3所示。

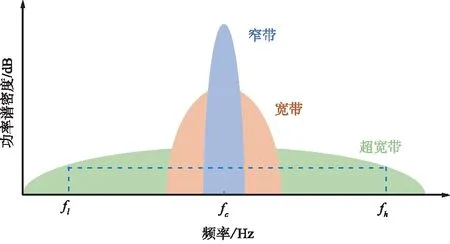
图3 超宽带/宽带/窄带信号比较模型Fig.3 UWB/wideband/narrowband signal comparison model

UWB信号相较于宽带和窄带信号拥有更丰富的频谱资源。UWB信号不需要依靠载频传输，在信号的发射端不需要混频器和振荡器将载波变换至所需频率波段，而在接收端则省略掉了载波恢复的步骤。相较于应用于室内定位中的其他技术，UWB室内定位系统结构更加简单且易于部署。

UWB的定位算法中，采用TWR算法无需时钟同步，测距精度较高，抗干扰能力强，且易于实现。TWR原理图如图4所示。

标签向基站发送一个轮询信号poll，经过Treply1的反应时间处理后，发送给标签一个回应信号response。标签从发送到接收信号的一个轮回时间是Tround1。接收到信号后，经过Treply1的处理时间标签再次向基站发送一个最终信号final。基站从发送到接收的一个轮回时间是Tround2，结束一次信号飞行时间的测量，从而得到信号的飞行时间:

(3)

然后，基于信号的传输时间解算出距离信息。

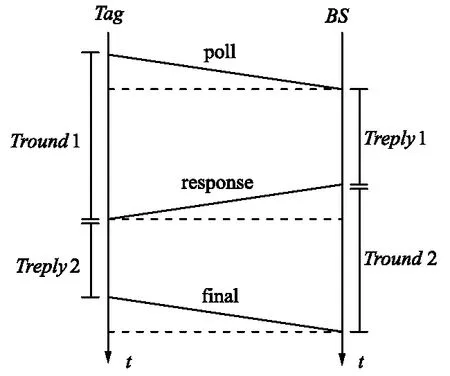
图4 TWR原理Fig.4 Schematic diagram of TWR

1.3 NLOS信号的检测

虽然UWB技术具有较强的抗干扰能力和抗多径衰弱能力，但是在NLOS情况下，UWB信号的测距定位能力将大大降低[15]。因此在进行UWB定位时，要进行NLOS的识别。在TWR的解算过程中，脉冲信号一共传递了3次。当出现障碍物遮挡时，信号的传输会多次受到NLOS的影响，相比于前一时刻的信号传播时间会出现较大的跳变。提出使用机器学习[16-17]的方式，利用SVM对实际场景中的NLOS和LOS情况下的距离测量值进行训练，得到符合对应应用场景的分辨阈值。由于移动障碍物可能会对UWB系统的NLOS测距结果产生规律性的影响，因此通过设置障碍物的位置模拟NLOS场景，并研究障碍物位置与NLOS检测之间的关系[18-19]。NLOS/LOS样点采集模型如图5所示。

图5 NLOS/LOS样点采集模型Fig.5 NLOS/LOS sample collection model

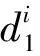
在NLOS情况下的测量误差曲线图如图6所示，其中横坐标表示测量范围，纵坐标表示测量值与实际值的差值，可以看出，在NLOS情况下会存在正误差，同时可以看出障碍物所在不同位置对测距精度的影响。

图6 NLOS环境下的测量误差Fig.6 Measurement error in NLOS environment

对应的测量值与实际值之间的比值情况曲线图如图7所示，纵坐标表示测量值与实际值的比值情况，且比值不低于1。比值曲线图相较于误差曲线图线条更加平滑，曲线的变化情况基本一致。

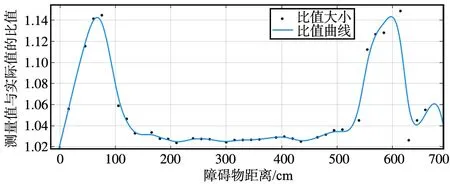
图7 NLOS测量值与实际值的比值Fig.7 Ratio of NLOS measured value to actual value

图8是在LOS情况下的测量误差，横坐标表示标签距离基站的距离，纵坐标表示测量值与实际值的差值，可以看出实验中的LOS情况下会存在负误差[20]。

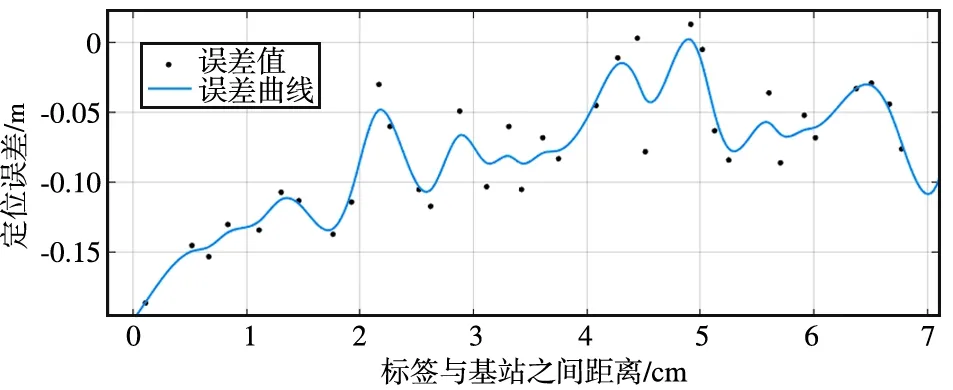
图8 LOS环境下的测量误差Fig.8 Measurement error in LOS environment

对应的测量值与实际值之间的比值情况曲线图如图9所示，纵坐标表示测量值与实际值的比值，且比值不超过1。误差曲线图的数据抖动存在一定的范围。测量值与实际值之间的比值比误差值更加平滑，更加符合SVM的阈值进行线性的划分。因此,选取测量值与实际值的比值作为SVM的训练样本。

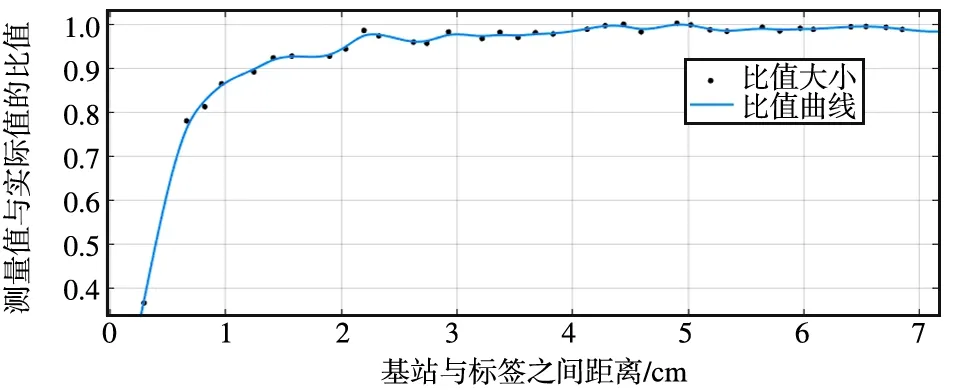
图9 LOS测量值与实际值的比值Fig.9 Ratio of LOS measured value to actual value

支持向量机的训练结果如图10所示。

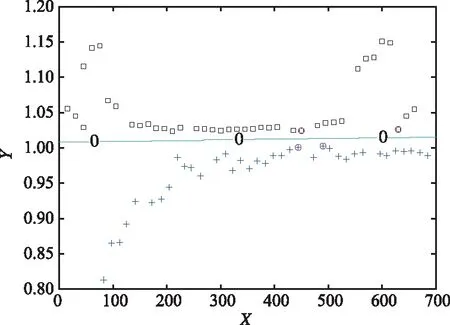
图10 支持向量机的分类结果Fig.10 Classification results of SVM

图中黑色方块为NLOS样本点，蓝色加号为LOS样本点，绿色线条为训练得到的阈值。分类结果显示，产生的阈值线条很好地区分了上半区域的NLOS样本点和下半区域的LOS样本点。

2 IMU和UWB融合定位策略

2.1 LS定位算法

基于UWB测得的基站到标签的3边距离，通过LS可以解算出标签的坐标。LS的具体算法如图11所示。

图11 最小二乘定位算法Fig.11 Least square positioning algorithm

LS的具体算法如下所示：

设在二维平面内目标Tag(x,y)和观测站BS(xn,yn)，通过计算可以得到二者之间的距离dn：

(4)

本文提出的新型分布式动态自组织网络的管理体系，基于自组织的DNA网络实现分布式的自组织网络和复杂动态网络的管理，从上往下均与最后一列相减后，用矩阵的形式可表示为：

(5)

(6)

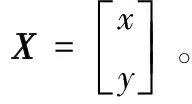
(7)

从而可以得到标签的坐标为：

X=(ATA)-1ATb。

(8)

2.2 LS与EKF融合定位

① EKF算法流程如下：

设置状态方程和观测方程分别为：

X(k+1)=ΦX(k)+ΓW(k)，

(9)

Y(k)=HX(k)+V(k),

(10)

式中，在离散时间k下的状态为X(k)；Φ为状态转移矩阵；Γ为噪声驱动矩阵；W(k)为白噪声。

得到的协方差预测和增益矩阵分别为：

P(k+1|k)=ΦP(k|k)ΦT+ΓQΓT，

(11)

K(k+1)=P(k+1|k)HT[HP(k+1|k)HT+R]-1。

(12)

状态更新和协方差更新分别为：

(13)

(14)

P(k+1|k+1)=[In-K(k+1)H]P(k+1|k)。

(15)

② LS-EKF算法流程如下：

将3个基站观测得到的距离信息d1，d2和d3作为观测向量，将IMU解算得到的水平和垂直方向的位移和速度作为状态向量X(k)=[xx(k)，xy(k)，vx(k)，vy(k)]T，其中基于速度的状态方程为：

(16)

表示成矩阵的形式：

X(k+1)=FX(k)+GW(k)，

(17)

(18)

设置标签到3个基站的距离信息的观测值作为观测向量，且表示为：

(19)

(20)

3 仿真设计和结果分析

为了验证所提出的算法的性能，通过仿真实验模拟场地的大小为6 m×6 m，假设运动是线性且匀加速的，标签初始化位置设置为参考坐标(0,0)。最初的水平和垂直方向的速度设置0.15 m/s，加速度设置为0.002 m/s2。在运行期间设置过程噪声的方差大小为Q=10-8，用来模拟真实场景下的标签运动轨迹。在使用传感器观测时，会存在一定的观测噪声，设置观测噪声的方差系数和2种情况。设置信号采样周期为t=1 s，并且总模拟时间为50 s，即采样次数为N=50。

在不同观测噪声下，通过LS和LS-EKF算法的定位轨迹如图12(a)所示。在同等观测噪声下,UWB和IMU经过EKF滤波过后的定位轨迹要比只经过LS定位算法的定位轨迹数据抖动更小，轨迹更加平滑。且观测噪声也会对定位结果有较大影响。图12(b)显示了2种算法的误差变化趋势，在观测噪声R=0.1时，经过LS算法定位的轨迹误差在0.1～1.4 m抖动，经过EKF滤波后定位误差下降并逐渐保持稳定在0.2～0.4 m。在观测噪声R=0.01时，LS-EKF算法的误差明显要比LS算法平滑得多，且定位误差更小。图12(c)是2种算法对应的误差累计分布函数(Cumulative Distribution Function，CDF)图，在观测噪声R=0.1时，LS和LS-EKF算法在仿真的数据范围内的最大误差分别为1.3 m和0.85 m；在观测噪声R=0.01时，LS和LS-EKF算法在仿真的数据范围内的最大误差分别为0.3 m和0.2 m。

(a) LS和LS-EKF定位轨迹

(b) 定位误差

(c) 累计误差分布函数图12 LS和LS-EKF定位算法Fig.12 LS and LS-EKF positioning algorithms

LS和LS-EKF算法平均误差和标准差如表1所示，在观测噪声R=0.1时，LS和LS-EKF算法平均误差为0.403 2 m和0.104 8 m，误差的标准差大小为0.074 4 m和0.028 5 m。在观测噪声R=0.01时，LS和LS-EKF算法平均误差为0.028 5 m和0.014 7 m，误差的标准差大小为0.007 7 m和0.001 8 m。在观测噪声分别为R=0.1和R=0.01时，相较于LS算法，LS-EKF算法的定位精度分别提高了74%和48%。

表1 LS和LS-EKF算法平均误差和标准差

4 结束语

本文基于对IMU和UWB传感器的研究，结合了UWB的高精度定位性能和IMU不受NLOS影响的特性，提出了一种基于传感器融合的室内导航定位系统。为了解决室内环境下的NLOS对定位的干扰，需要先进行NLOS的识别。通过对NLOS和LOS情况下的测距研究，基于测量值与实际值的不同比值作为样本点，应用SVM的机器学习方式提出了一种适用于特定实验场景下的NLOS的识别方法，能够有效地识别NLOS信号。随后在LOS场景下基于LS和EKF算法提出了一种LS-EKF算法，实验仿真结果表明,提出的LS-EKF算法相较于LS算法定位精度提高了48%～74%。