基于高低轨场景的干扰源三维坐标定位方法

陈 兵，邵 芳，戴欧志雄，霍立寰，柏如龙，黄鹏辉

(1.中国电子科技集团公司第五十四研究所，河北 石家庄 050081;2.河北省电磁频谱认知与管控重点实验室，河北 石家庄 050081;3.中国人民解放军32027部队，河南 开封 475000;4.上海交通大学 电子信息与电气工程学院，上海 200240)

0 引言

卫星通信利用人造地球卫星作为中继站转发无线电波，从而使地球站间能够进行业务通信。卫星通信具有覆盖范围广、通信容量大、传输质量好和组网方便迅速的优点，自20世纪90年代以来得到了迅猛发展。然而，由于卫星通信具有开放性的特点，易受到干扰信号的干扰。尤其出现恶意干扰信号时，卫星通信的正常业务将受到严重的影响。因此，卫星通信迫切需要干扰源定位的方法，以对非法干扰源信号采取查证、定位和遏制措施[1]。

基于卫星平台的干扰源定位技术通过主邻星被动接收干扰源信号，基于时频差测量定位技术，能够对干扰源进行准确定位，在很多领域已经发挥了重要作用[2-4]。以往的卫星干扰源定位研究大多数集中在零高程假设的定位算法推导，或已知初始高程信息的定位算法设计，难以对干扰源进行准确的三维坐标定位[5-18]。钟丹星等[7-8]基于地球WGS-84椭球模型，提出了三星时差定位的牛顿迭代方法。该方法先采用球面模型粗定位，然后在WGS-84球面模型下进行精确求解。然而，该方法仅适用于零高程假设的目标。林雪原等[11-12]基于数字地图以及WGS-84坐标系，提出了一种数字地图辅助的三星时差定位方法，能够在数字地图中高程信息已知的情况下实现精确定位。然而，该方法需要已知干扰源区域的数字地图高程值。当干扰源高程信息缺失时，该类算法误差较大，并且对位于高空的待定位目标，定位精度严重恶化。

针对这一问题，本文提出了一种基于高低轨场景的干扰源三维坐标定位方法。首先获得低轨卫星过顶期间测量得到的多个时差测量值，建立高低轨场景下的时差定位方程组，然后基于牛顿迭代法推导了迭代公式，设计了工程化定位步骤。该方法能够在利用共视时间内的多组时差测量结果，准确计算得到目标的三维位置坐标，在存在时差测量误差情况下，仍具有良好的稳健性。

1 高低轨定位模型

三星干扰源定位示意如图1所示，高轨卫星能够持续接收到目标信号，低轨卫星在过顶时能够接收目标信号旁瓣。

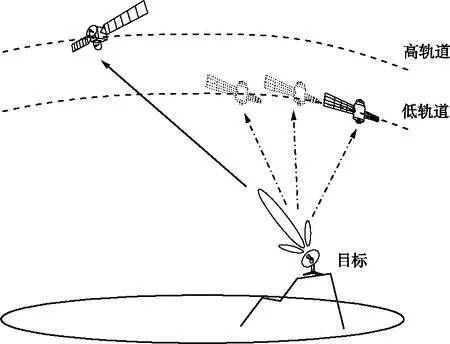
图1 三星干扰源定位示意Fig.1 Configuration of tri-satellite interference source localization

假设干扰源在大地坐标系下的经纬度为(L,B,H)，转换为地心地固坐标系下对应的三维坐标为(x,y,z)，第p个时刻的高轨主星坐标为(xp,0,yp,0,zp,0)，低轨邻星坐标为(xp,1,yp,1,zp,1)，干扰源与高轨主星和低轨邻星在第p个时刻的时差值为τp，满足：

τp=(rp,1-rp,0)/c，

(1)

式中，c为光速；rp,0和rp,1分别为干扰源与高轨主星、低轨邻星在第p个时刻的距离：

(2)

(3)

设第p个时刻的高轨主星坐标为(xp,0,yp,0,zp,0)，低轨邻星坐标为(xp,1,yp,1,zp,1)，目标坐标为(x,y,z)，根据距离计算公式，能够得到以下定位方程组：

(4)

三星时差线相交情况示意如图2所示。低轨卫星过顶时，在目标高程先验已知时，低轨天线接收信号与高轨天线接收信号相关测量得到的时差线、多时刻时差线交会于目标位置。因此，基于低轨卫星过顶时测量得到多个时刻的时差结果，高低轨场景具备对目标定位条件。

图2 多时刻三星时差线相交情况示意Fig.2 Intersection of TDOA lines in multiple moments

2 迭代求解算法

针对多时刻的测量结果构成的定位方程组，直接求解较为困难，考虑采用牛顿迭代方法求解。将式(4)进行如下表示：

(5)

式中，τ′p为第p个时刻的时差测量值。

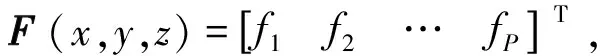
F(x,y,z)=0。

(6)

相应的海森矩阵为：

(7)

若第k次迭代中干扰源坐标为Pk=(xk,yk,zk)，则根据下式进行迭代：

Pk+1=Pk-pinv[F′(xk,yk,zk)]F(xk,yk,zk)，

(8)

式中，pinv[·]为求伪逆操作。综上，本文提出的目标三维坐标定位方法流程如图3所示。

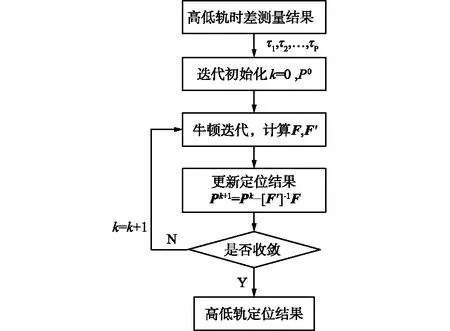
图3 基于高低轨场景的干扰源目标定位流程Fig.3 Flow chart of interference source localization in high-and-low orbit scenario

算法流程如下：

① 根据P个时刻的时差τ′p，计算高轨主星和低轨邻星与干扰源目标的路程差(rp，1-rp，0)；

② 初始化迭代次数k=0，以及干扰源的初始坐标P0；

③ 根据式(7)获得该次海森矩阵F′(xk,yk,zk)，基于式(8)计算目标位置估计结果Pk+1；

④ 定义迭代位置误差δ，若δ小于门限，则终止迭代并输出定位结果；否则，令k=k+1，返回步骤③继续迭代，其中，

3 仿真实验

高轨卫星的星下点经度约为150°E，低轨卫星选取某民用低轨卫星，轨道高度约为907 km，选择STK对高低轨定位的场景进行仿真构建，定位场景如图4所示。干扰源目标经度118.15°E，纬度30.48°N，高度3 864.8 m。根据STK仿真卫星运行轨迹和波束覆盖情况，当时间为21：27—21：38时，目标处于低轨星波束和高轨波束的共视区，此时能够进行高低轨联合定位。

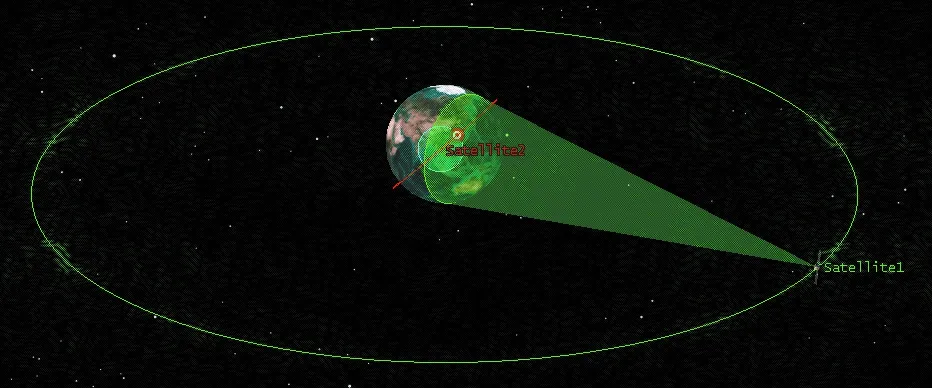
图4 STK高低轨定位示意Fig.4 Configuration of the high-and-low orbit interference localization in STK

在仿真实验中，三维定位误差σE表示为：

(9)

3.1 算法有效性验证实验

干扰源位置为118.15°E，30.45°N，高度3 864.8 m，时差测量误差为2 μs，星历位置误差为1 km。图5(a)给出了低轨星过顶过程中，各个时刻时差线的交会情况。可以发现，由于时差线无法考虑高程影响，所以时差线并不能交汇于目标位置。图5(b)给出了高低轨联合算法在迭代过程中，三维定位误差随迭代次数的变化变换关系。可以发现，算法收敛迅速，并且能够在5次时实现收敛。定位结果随迭代次数的变化关系如表1所示。在第5次时的三维定位误差为0.46 km。

(a) 多时刻时差线相交情况

(b) 三维定位误差随迭代次数变化图5 高低轨场景下的定位结果Fig.5 Localization results in high-and-low orbit scenario

表1 定位结果随迭代次数变化

3.2 影响因素分析实验

高低轨场景下的定位误差影响因素主要包括时差测量误差和星历误差，下面通过蒙特卡洛实验对这2种误差的影响程度进行具体分析，高低轨场景定位性能影响实验结果如图6所示。

(a) 定位误差随星历误差变化

(b) 定位误差随时差测量精度变化图6 高低轨场景定位性能影响实验结果Fig.6 Performance impact simulation in high-and-low orbit scenario

干扰源位置为118.15°E，30.45°N，高度为3 864.8 m，蒙特卡洛实验次数为1 000。首先仿真高低轨场景下定位误差随星历精度的变化关系，时差测量误差为2 μs，可以发现，星历误差增加时，三维定位精度逐渐增大；在小测量误差情况下，星历误差与定位误差基本一致。然后仿真了星历误差1 km时，高低轨的三维定位误差随时差测量精度的变化关系，可以发现，由于采用了多个时刻的时差结果进行联合定位，在时差测量精度为10 μs的情况下，三维定位误差仍然能够达到2.5 km以内。

4 结束语

基于卫星平台的干扰源定位方法具有覆盖范围广、隐蔽性强的优点。然而，传统方法往往基于零高程假设，对于实际干扰源定位误差较大。针对这一问题提出了一种基于高低轨场景下的多时差定位方法，该方法利用低轨卫星过顶期间测量得到的多个时差测量值，构建高低轨时差定位方程组，然后基于牛顿迭代法推导了迭代公式，能够获得干扰源目标的三维坐标。仿真实验基于STK工具，构建了实际的高低轨定位场景，并进行了定位精度仿真和影响因素分析，验证了所提方法的有效性和稳健性。同时，基于所提的定位误差分析方法，能够为后续卫星轨位设计、定位时刻选择等工程化应用提供技术支撑。