一类重心权Hermite有理插值的二阶导数收敛性

康宁，荆科

（1.南京财经大学经济学院，江苏 南京 210023； 2.南京财经大学应用数学学院，江苏 南京 210023）

一类重心权Hermite有理插值的二阶导数收敛性

康宁1，荆科2

（1.南京财经大学经济学院，江苏 南京 210023； 2.南京财经大学应用数学学院，江苏 南京 210023）

研究了一类特殊情形的重心权Hermite有理插值，证明了该插值函数的二阶导数在插值节点和非插值节点处分别以和的速度收敛于函数。数值例子进一步验证了方法的有效性。

重心权有理插值；Hermite插值；收敛速度；二阶导数

0 引言

并给出了插值函数在插值区间内无极点的必要条件和具有重心权形式的充分条件，遗憾的是，该插值方法虽然解决了计算复杂性问题，但逼近误差可能较大。为解决重心权Hermite有理插值在实数范围内无极点以及收敛性问题，文献［3］给出了一种Hermite有理插值的Newton形式。文献［5-7］提出了一种重心权Hermite有理插值的迭代构造方法，并研究了度量数值稳定性的Lebesgue常数性质。文献［8］针对一类特殊情形的Hermite插值，证明了的收敛速度为，并给出了具有较高数值稳定性和较低计算复杂度的重心权函数式：

上述研究结果极大地丰富了重心权Hermite有理插值的理论方法，但研究重点集中在重心权Hermite有理插值函数及其一阶导数的收敛性上。鉴于此，本文进一步探讨文献［8］中的重心权Hermite有理插值，并证明重心权Hermite有理插值的二阶导数同样具有高阶收敛性质，以丰富已有研究成果。

1 收敛性质

由文献［9］Hermite多项式插值的误差公式：

得到式（2）的重心权Hermite有理插值的误差估计：

为解决式（3）的极限问题，定义函数：

另外，由文献［10-11］中拟等距节点的定义，有

其次，将式（8）分为4项：

依次证明各项的收敛性质。

其中，

又因文献［8］式（3.10）已获证

同理，

其中，

然后，对i赋值，可得

同理，

最后，与式（11）类似，可得

同理，

综上，定理2得证。

2 数值例子

采用Matlab软件进一步验证重心权Hermite有理插值的二阶导数收敛性质，并将其应用于2个经典的函数实例，见表1。

表1 函数、参数和插值节点Table 1 Functions ， parameters ， and interpolation nodes

表1 函数、参数和插值节点Table 1 Functions ， parameters ， and interpolation nodes

实验函数参数插值区间插值节点xi12

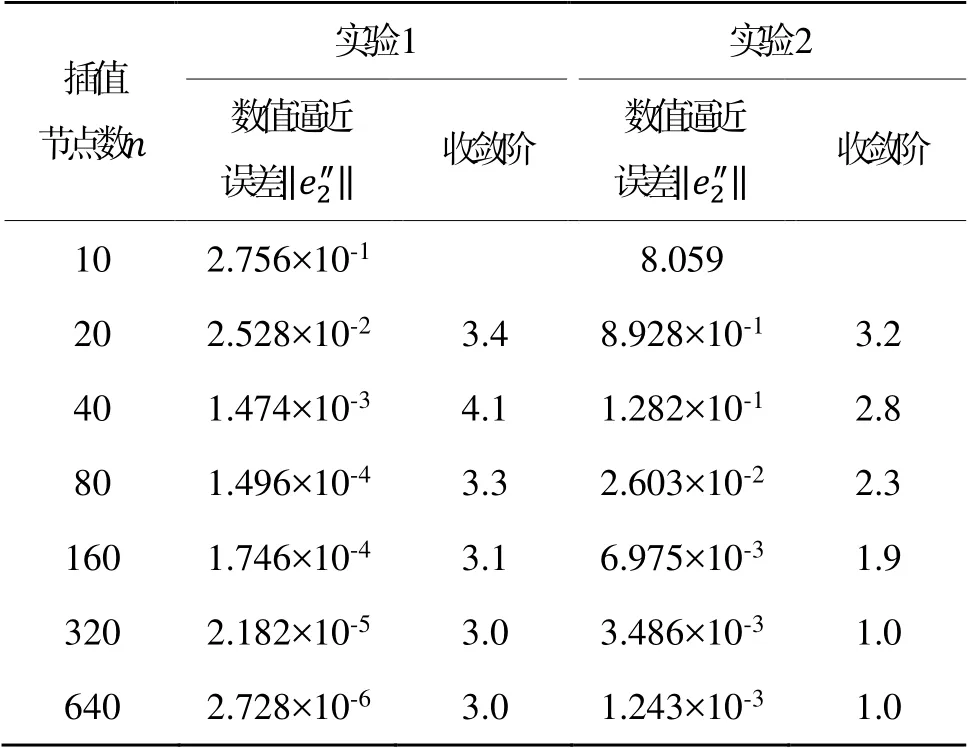
表2 逼近误差和收敛阶Table 2 Approximation errors and convergence orders

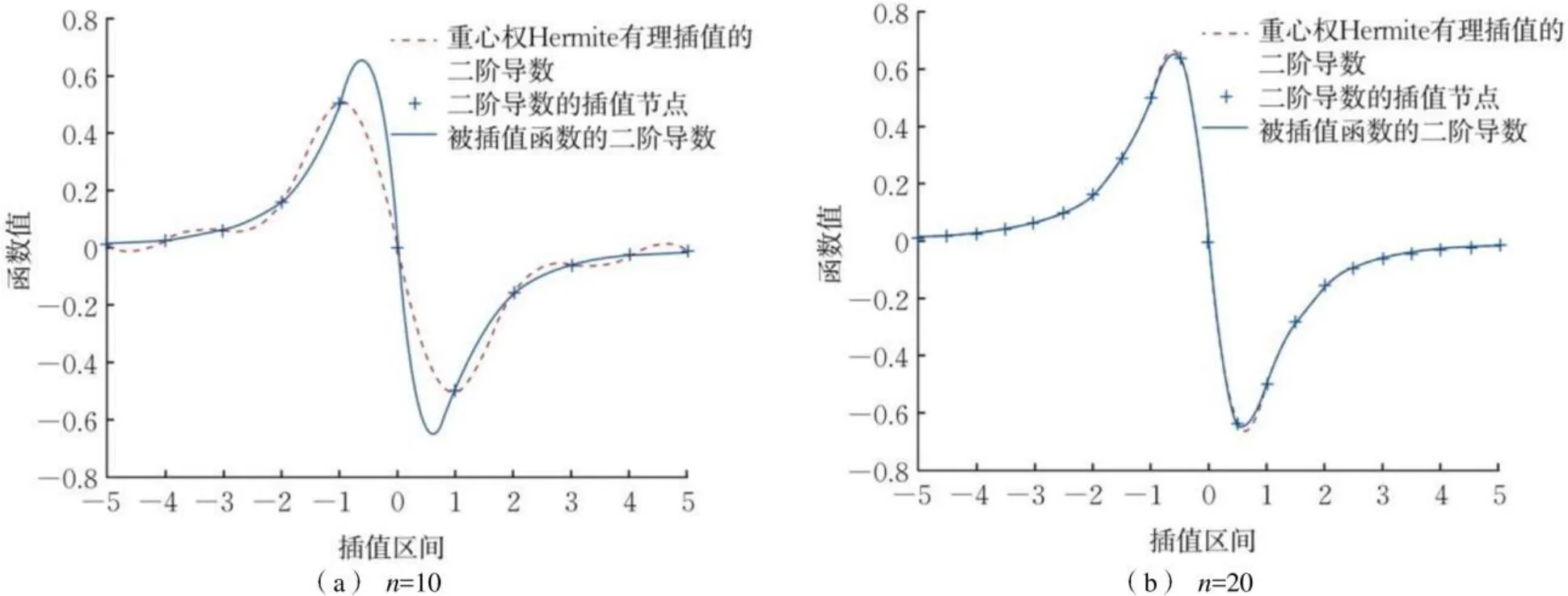
图1 实验1中重心权Hermite有理插值的二阶导数曲线Fig.1 Plot of the second derivatives of barycentric Hermite rational interpolation in experiment 1

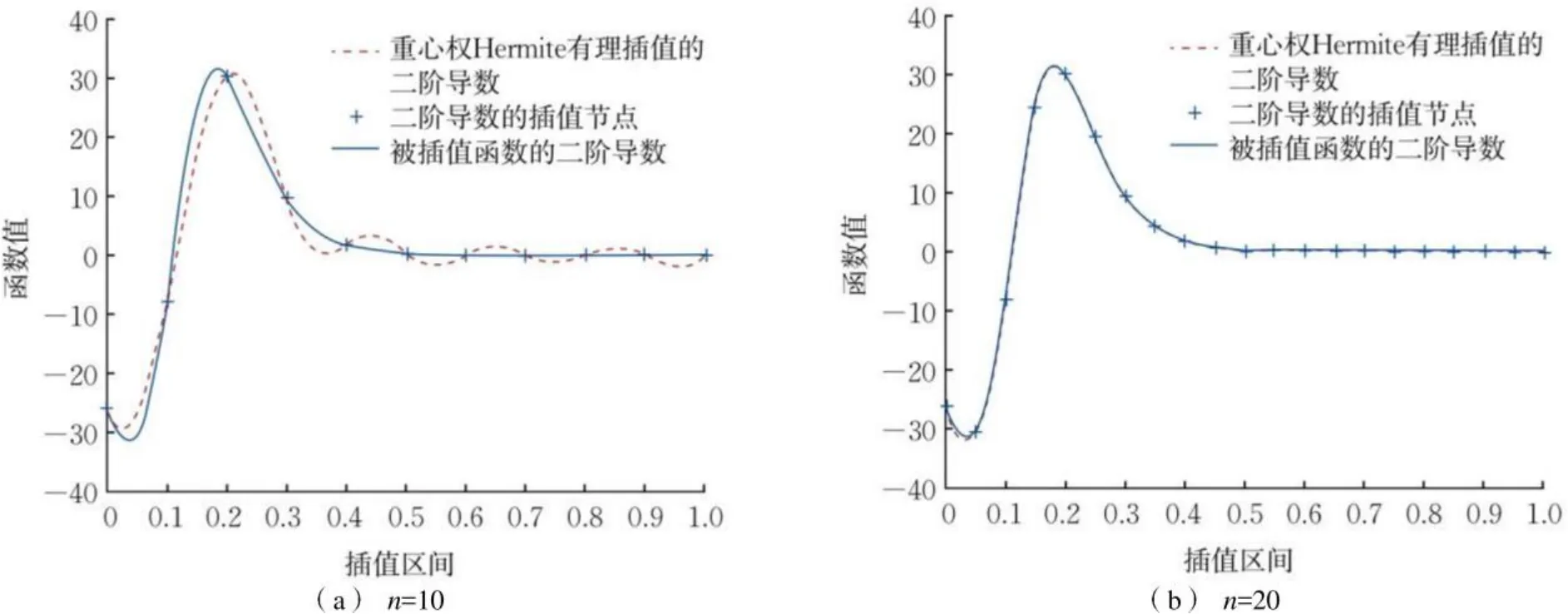
图2 实验2中重心权Hermite有理插值的二阶导数曲线Fig.2 Plot of the second derivatives of barycentric Hermite rational interpolation in experiment 2

由表2及图1、图2可知，重心权Hermite有理插值的二阶导数的数值逼近误差及收敛阶支持定理1和定理2，进一步验证了本文方法的有效性。

3 结论

［1］SZABADOS J. On the order of magnitude of fundamental polynomials of Hermite interpolation［J］. Acta Mathematica Hungarica， 1993，61（3/4）：357-368. DOI：10.1007/bf01874691

［2］CIRILLO E. Advances in Barycentric Rational Interpolation of a Function and Its Derivatives［D］. Lugano： Università della Svizzera Italiana，2019.

［3］SCHULZ C. Topics in Curve Intersection and Barycentric Interpolation［D］. Oslo： University of Oslo，2009.

［4］SCHNEIDER C， WERNER W. Hermite interpolation：The barycentric approach［J］. Computing，1991， 46（1）：35-51. DOI：10.1007/BF02239010

［5］CIRILLO E， HORMANN K. An iterative approach to barycentric rational Hermite interpolation［J］. Numerische Mathematik， 2018，140（4）： 939-962. DOI：10.1007/s00211-018-0986-y

［6］CIRILLO E， HORMANN K，SIDON J. Convergence rates of a Hermite generalization of Floater-Hormann interpolants［J］. Journal of Computational and Applied Mathematics， 2020，371： 112624. DOI：10.1016/j.cam.2019.112624

［7］CIRILLO E， HORMANN K. On the Lebesgue constant of barycentric rational Hermite interpolants at equidistant nodes［J］. Journal of Computational and Applied Mathematics， 2019，349： 292-301. DOI：10.1016/j.cam.2018.06.011

［8］JING K， KANG N，ZHU G Q. Convergence rates of a family of barycentric osculatory rational interpolation［J］. Journal of Applied Mathematics and Computing， 2017，53（1）： 169-181. DOI：10.1007/s12190-015-0962-y

［9］ATKINSON K E. An Introduction to Numerical Analysis［M］. New York： John Wiley amp; Sons，1989： 131-196.

［10］KLEIN G， BERRUT J P. Linear rational finite differences from derivatives of barycentric rational interpolants［J］. SIAM Journal on Numerical Analysis，2012， 50（2）：643-656. DOI：10.1137/110827156

［11］HORMANN K， KLEIN G，MARCHI S D. Barycentric rational interpolation at quasi-equidistant nodes［J］. Dolomites Research Notes on Approximation， 2012，5（1）： 1-6. DOI：10.14658/pupj-drna-2012-1-1

Convergence of second derivative of a family of barycentric Hermite rational interpolants

KANG Ning1, JING Ke2

（1. School of Economics，Nanjing University of Finance and Economics，Nanjing210023，China；2. School of Applied Mathematics，Nanjing University of Finance and Economics，Nanjing210023，China）

In this paper, we further study a family of barycentric Hermite rational interpolants in a special caseand prove that the second derivativesof interpolation function converges to corresponding functionat the rate ofandat interpolation nodes and non-interpolation nodes, respectively. Finally, numerical examples further verify the effectiveness of the method.

barycentric rational interpolation; Hermite interpolation; convergence rates; second derivatives

O 241.3

A

1008⁃9497（2022）03⁃324⁃05

10.3785/j.issn.1008-9497.2022.03.009

2021⁃04⁃06.

国家自然科学基金资助项目（11601224）；教育部人文社科项目（18YJC790069）；江苏省高等学校自然科学研究项目（18KJD110007）；国家统计局项目（2018LY28）.

康宁（1986—），ORCID：https：//orcid.org/0000-0002-2905-6193，女，博士，副教授，主要从事应用数值逼近、统计计算研究，E-mail：9120171058@nufe.edu.cn.