表征学习驱动的多重网络图采样
2022-06-02虞瑞麒刘玉华沈禧龙翟如钰张翔周志光
虞瑞麒,刘玉华*,沈禧龙,翟如钰,张翔,周志光
(1.杭州电子科技大学数字媒体与艺术设计学院,浙江 杭州 310018;2.浙江财经大学信息管理与人工智能学院,浙江 杭州 310018)
表征学习驱动的多重网络图采样
虞瑞麒1,刘玉华1*,沈禧龙2,翟如钰1,张翔2,周志光1
(1.杭州电子科技大学数字媒体与艺术设计学院,浙江 杭州 310018;2.浙江财经大学信息管理与人工智能学院,浙江 杭州 310018)
已有的图采样方法侧重于单图采样,关注如何在一张图上通过采样保留其特定的拓扑结构特征。随着数据采集能力的提升,多重网络图在实际应用中越来越普遍,即相同的节点集在不同场景中具有不同的网络关系。针对传统图采样方法无法兼顾多重网络图结构特征的问题,提出了表征学习驱动的多重网络图采样算法。首先,设计融合多重网络图结构特征的图表征学习方法,将节点投影至二维的表征学习空间;其次,利用改进的自适应蓝噪声采样算法,考虑节点密度和网络连通性,从表征学习空间筛选节点,以保持其多重网络结构特征及图上下文结构特征。进而开发了一套多重网络图采样可视分析系统,支持用户交互式地探索多重网络图采样,并与已有采样算法进行对比。案例分析和评估实验证明了本文算法在多重网络图采样中的有效性。
多重网络图;图采样;可视分析;评估
网络图是一种常见的数据结构,可对实体与实体之间的关联关系进行有效建模,广泛应用于社交媒体、地理交通和生物医学等领域。随着数据采集能力的提升,网络图的规模不断增大,结构也变得越来越复杂,这不仅加重了网络图特征分析的计算负担,也严重影响了网络图的视觉表达[1]。因此,提出了一系列图采样方法[2],从原始网络中选取部分具有代表性的节点和边以简化和稀疏大规模网络图。
在实际应用场景中,节点之间的关系可能不止一种,这种具有多种关联关系的节点构成了一组多重网络[3]。例如,同一组社交用户群体分别在使用QQ、微信和微博等不同社交软件,并在不同的社交媒体平台上拥有不同的好友关系,由此产生的多种社交关系网就是典型的多重网络。
传统的图采样算法都是单图采样,即关注如何在一张网络图上通过采样保留其特定的拓扑结构特征,如度分布、聚类系数、平均路径长度等。如果直接将单图采样算法分别应用于多重网络的每一重图,则会令采样得到的节点集不一致,增大图采样结果的存储空间,也会造成采样分析和探索不连贯。如果只对多重网络中的某张图进行采样,然后依据该结果重构其他图的采样网络关系,会造成采样参照的网络图结构特征保持相对较好,而其他图的结构特征极易丢失。因此,传统的图采样算法不适用于多重网络图,不利于多重网络图的联合采样分析。
为解决以上问题,本文提出表征学习驱动的多重网络图采样算法。首先,设计多重网络图表征学习方法,综合考虑多重网络的结构特征,将所有节点投影至二维表征学习空间;其次,利用和改进经典的自适应蓝噪声采样算法,考虑节点密度和网络连通性,从二维表征学习空间中启发式地筛选出部分节点,以实现多重网络图上下文结构特征的同步保持;进一步,开发了一套多重网络图采样可视分析系统,支持用户交互式地探索和评估多重网络图的采样结果,将其与已有采样算法进行对比。基于真实数据的案例分析和量化实验均显示,本文算法在进行多重网络图采样时是有效的,其重要节点、网络连通和社区相似性等多项指标均优于传统的图采样算法。
1 相关工作
1.1 图采样算法
传统的图采样算法可分为三类。(1)基于点的采样[4],在原始网络图中随机选取一组节点,再添加与之关联的边生成采样图。(2)基于边的采样[5],在原始网络图中随机选取一组边,再添加与之对应的节点生成采样图。(3)以上方法获得的采样图其连通性往往难以保持,为此提出基于游走的采样[6],首先在图中随机选取1个节点,然后基于一定的遍历策略从当前节点的邻居节点中随机选取1个节点作为下一个采样节点,不断迭代以上过程,实现图采样。
在可视化领域,图采样已广泛应用于大规模复杂网络图的简化表达,通过降低点线交叉重叠引起的视觉混淆,增强用户对网络结构的认知和理解。HU等[7]提出基于图连通性的光谱顶点采样算法,能较好地保持原始网络图的连通性和全局拓扑结构。ZHOU等[8]设计了多目标的自适应蓝噪声采样算法,降低人群移动网络的规模,同时保持空间分布特征和社区结构的一致性。GUO等[9]提出了流采样算法,对大规模迁徙网络进行简化表达,改进和利用核密度模型,提取和展示重要边。ZHAO等[10]提出了小结构保持的图采样算法,尽可能保留原始图中的少数结构,如桥节点、边缘节点和高度节点。ZHOU等[1]基于图表征学习,提出了保持上下文结构特征的采样算法,在保留全局结构的同时有效保持聚类密度等特征。
但以上算法均侧重于解决单一网络的采样问题,关注的是如何提高单图的采样效率或如何保持特定的拓扑结构特征。
1.2 图采样评估
为检验图采样算法的有效性,研究者从结构属性和视觉感知角度出发,设计和提出了多种图采样评估指标。一类是由图的结构属性特征驱动的采样评估。例如,MAYIA等[11]利用节点度分布、聚类质量和网络覆盖度等指标,对几种基于遍历的图采样算法进行了评估。另一类是由用户视觉感知驱动的采样评估。NGUYEN等[12]借助代理图的概念提出了基于形状的视觉质量指标,并对比了不同图采样算法对样本视觉质量的影响。WU等[13]通过用户实验总结了影响图采样视觉感知的多项指标,并进一步探索了传统图采样策略在这些指标上的表现力。ZHANG等[14]提出了一套视觉感知标准,包括聚类的大小、形状和数量等,评估了图采样算法在视觉特征保留上的有效性。
1.3 图表征学习
图表征学习广泛应用于网络分析领域,关注如何获取网络节点在低维空间中的向量表示,帮助用户理解和探索在向量空间中的网络结构。根据实现原理,图表征学习大致分为三类。(1)基于矩阵分解的表征学习[15],以矩阵形式表示网络节点之间的结构关系,并通过矩阵分解的方式生成节点向量;(2)基于随机游走的表征学习,通过随机游走的方式得到节点序列集合,根据节点之间的共现关系估计节点的向量表示,最典型的有DeepWalk[16]和node2vec[17];(3)基于深度学习的表征学习[15],能对网络图中的非线性结构进行建模,并通过深度自编码器和自解码器学习和获取节点的向量化表示。
2 多重网络图采样算法
多重网络图采样算法流程如图1所示,包括融合多重网络图结构特征的表征学习和基于表征学习空间的多重网络图采样。
2.1 融合多重网络图结构特征的表征学习
利用node2vec[17]的游走策略将多重网络图结构特征转换至统一的向量化空间,如图1(b)所示,在保持多重网络图上下文结构的同时,为后续采样提供遍历基础和搜索空间。步骤如下:
Step 1 生成序列样本集。首先,假设t为上一个访问节点,当前随机游走经过边(t,v),到达节点v,而由v经过边(v,x)跳转至下一节点x的概率为
其中,dtx为t与x之间的最短路径。由式(1)知,当dtx为0时,t和x为同一个节点,此时参数p控制的是已访问节点的概率,即返回概率,且p越大,游走访问新节点的概率越高。当dtx为1时,t和x相连,默认跳转概率为1。当dtx为2时,t和x不相连,参数q控制的是随机游走的方向策略。当qgt;1时,倾向于访问与t接近的节点,反映广度优先的遍历特性;当qlt;1时,倾向于访问远离t的节点,反映深度优先的遍历特性。
由式(1)设置归一化v跳转至各邻居节点的概率,在随机跳转至下一节点后按照相同方式访问其他节点,直至达到随机游走的最大路径长度L,一条序列样本生成完毕。接着以任一节点为源节点,利用上述游走策略在每一重网络背景下生成对应的序列样本。最终将这些样本组成完整的多重网络图序列数据集,作为下一步表征学习的输入。
Step 2 向量化表示。基于获得的所有序列样本集,设置目标函数:
其中,f(u)表示将节点u映射为向量的函数,Ns(u)表示和u出现在同一条序列样本中的邻近节点集合,即在给定某个节点的条件下,使其所在序列样本集中其他节点出现的概率最大。用Skip-Gram模型训练输入序列样本集,最终得到每个节点的向量化表示。
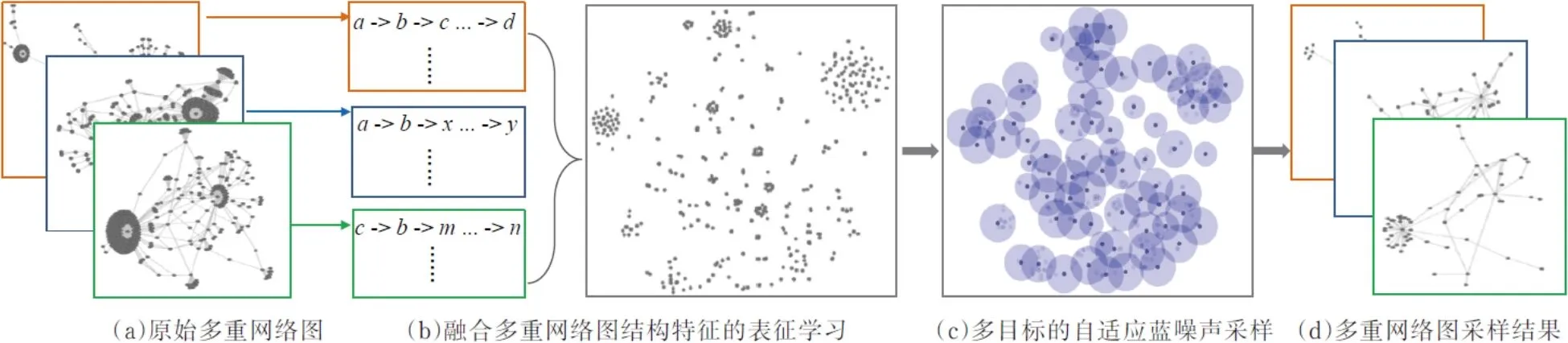
图1 多重网络图采样算法流程Fig.1 Flow chart of the multiple graph sampling
Step 3 降维。经以上2个步骤将多重网络图的所有节点转化为高维向量,同时保留每一重图的上下文结构特征,如果在大部分网络背景下2个节点处于邻近关系,那么它们在向量空间中的分布也接近。采用分布式随机邻居嵌入(t-distributed stochastic neighbor embedding,t-SNE)[18]算法将节点的高维学习向量投影至二维平面,为下一步采样做准备。
2.2 基于表征学习空间的多重网络图采样
2.2.1 保持上下文结构特征的采样
基于二维表征学习空间,采用自适应蓝噪声采样算法筛选节点,尽可能保留和覆盖原始多重网络图上下文结构特征,如图1(c)所示。
Step 1 随机选择一个节点u,并以此为中心构造一个半径为r的泊松盘,且r=ra/den(u),ra为由用户设置的可以调整采样率的参数,采样率越大,ra越小,泊松盘就越小。den(u)代表节点u所处局部区域的节点密度,即以u为圆心、ra为半径的圆包含的节点数量。密度越大,泊松盘的尺寸就越小,在泊松盘内随机选择一个节点作为该局部区域的代表性节点。
Step 2 在选择代表性节点后,将其所在泊松盘内的其他节点标记为非活动节点,再将位于圆盘ra和2ra之间环形区域的节点标记为活动节点。随机选择一个活动节点按照step 1构造新的泊松盘,并随机选择代表性节点。
Step 3 重复以上2个步骤,直至所有节点被标记为代表性节点或非活动节点,采样结束。
综上可知,传统的蓝噪声采样算法可较好地覆盖整个数据空间,还可根据节点疏密自适应地调整采样圆盘大小,进而控制采样节点的数量,保证节点密度分布的一致性。
2.2.2 多目标采样优化
基于向量化空间的蓝噪声采样在保持多重网络图上下文结构特征上具有一定优势,但在结构连通性保持上存在明显不足。例如,具有较大中介度的节点(桥节点),在网络连通中很重要,但在泊松盘内随机选择代表性节点时易被忽略。此外,蓝噪声采样过程没有考虑多重网络图的复杂连接关系,使得多重网络图的连通性保持存在较大的不确定性。为此,做以下两点改进以增强多重网络图连通性的同步保持。
⑪项贤明:《教育全球化全景透视:维度、影响与张力》,《北京师范大学学报》(社会科学版)2008年第1期。
(1)增加桥节点被选择的概率。在采样模型中加入中介度分析,计算每一重图所有节点的中介度(即任意两节点间的最短路径经过该点的次数),并做归一化处理。节点u在多重网络图中的综合中介度定义为其在每一重图中的中介度总和。记bet (u)为节点u所处局部区域的连通重要性,即以u为圆心、ra为半径的圆包含的所有节点的平均综合中介度。对以u为中心的泊松盘的半径进行优化:
其中,α和β为密度和连通重要性的权重,且满足α+β=1.0,α不为0,初始设置α=β=0.5。若某个泊松盘包含桥节点的数量越多,则泊松盘的半径将相应减小,进一步,保证盘内节点的综合中介度与采样概率成正比,从而有效增加桥节点被选为代表性节点的概率。如图2(a)所示,优化前,以u为圆心的泊松盘半径相对较大,当随机选择一个代表性节点时,容易丢失节点u邻域范围内的多个桥节点(黑色圆点)。优化后的泊松盘如图2(b)所示,以u为圆心的泊松盘半径减小,同时周边区域需要填充的泊松盘数量增加,使得分处不同小盘内的多个桥节点都有较大概率成为代表性节点,从而增加了采样结果中桥节点的数量。
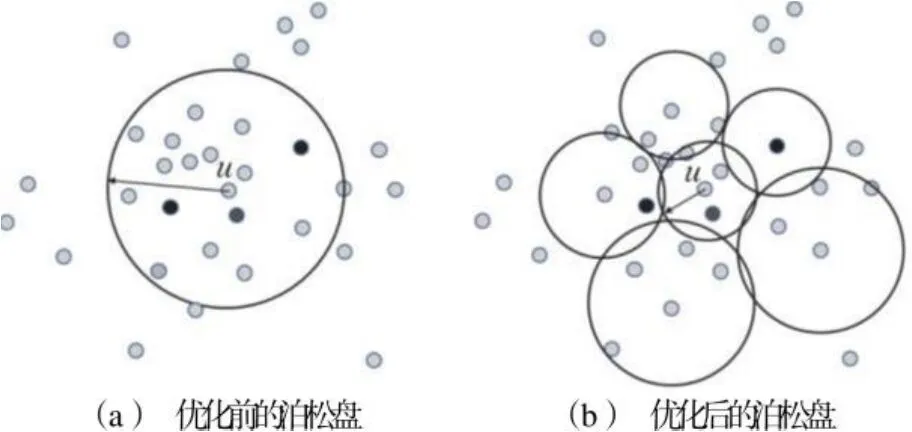
图2 泊松盘优化Fig.2 Optimization of the Poisson disks
(2)考虑多重网络图的同步连通性。虽然在向量化空间中,彼此邻近的节点之间相互连接的可能性较高,但由于采样的随机性,难以保证多重网络图在不同网络结构上连接。因此,当一个泊松盘向外拓展确定另一个泊松盘时,需遍历其周边多个不同的泊松盘,同时考虑其包含的节点与当前泊松盘内代表性节点在多重网络图上的连接关系。如图3所示,中间黑实线圆为当前的采样圆盘,黑圆点为选中的代表性节点。假定当前为3重网络图,在周边预设的多个不同泊松盘(虚线圆)中,三角形节点表示与之前的代表性节点在每一重图上均存在连接关系,图3右侧图例中,三角形后面的每个方框表示其中1重网络图,对号表示在对应网络图上连接,叉号表示不连接。菱形节点表示与代表性节点在其中2重网络图上存在连接,圆形节点表示与代表性节点在其中1重网络图上存在连接。如果周边某个泊松盘包含与上一个代表性节点在所有图(或数量较多的图)上都存在连接关系的节点且节点数量较多,那么这个泊松盘将优先作为下一个采样圆盘。相比于其他采样圆盘,在该圆盘内选择某个代表性节点维持多重网络图同步连通性的概率更大。如图3所示,箭头指向的右侧圆盘包含2个与中心圆盘黑色代表性节点在3重网络上都连接的节点,因此优先选中作为下一个采样盘。
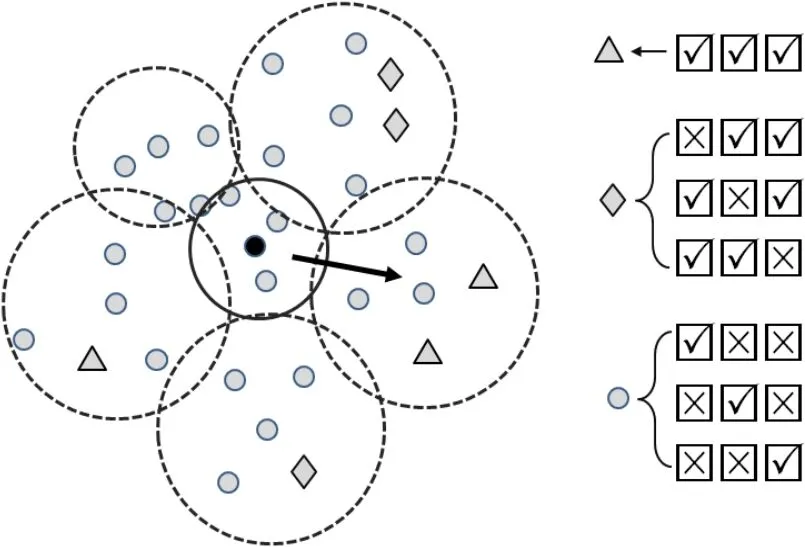
图3 考虑多重网络图连通性的泊松盘遍历Fig.3 Traversal across different Poisson disks for the retention of multiple graph connection.
3 多重网络图采样可视分析系统
多重网络图采样可视分析系统如图4所示。
3.1 多重网络图数据集
系统内置2套多重网络图数据集(https://manliodedomenico.com/data.php)。第一套是热点Twitter转发数据集MOSS,从中选取400个用户,根据转发、提及和回复构造3重网络。第二套是线虫连接体数据CELE,包含237个神经元节点,通过不同的信号传递方式(电突触、化学突触和多元突触)构建3重网络。
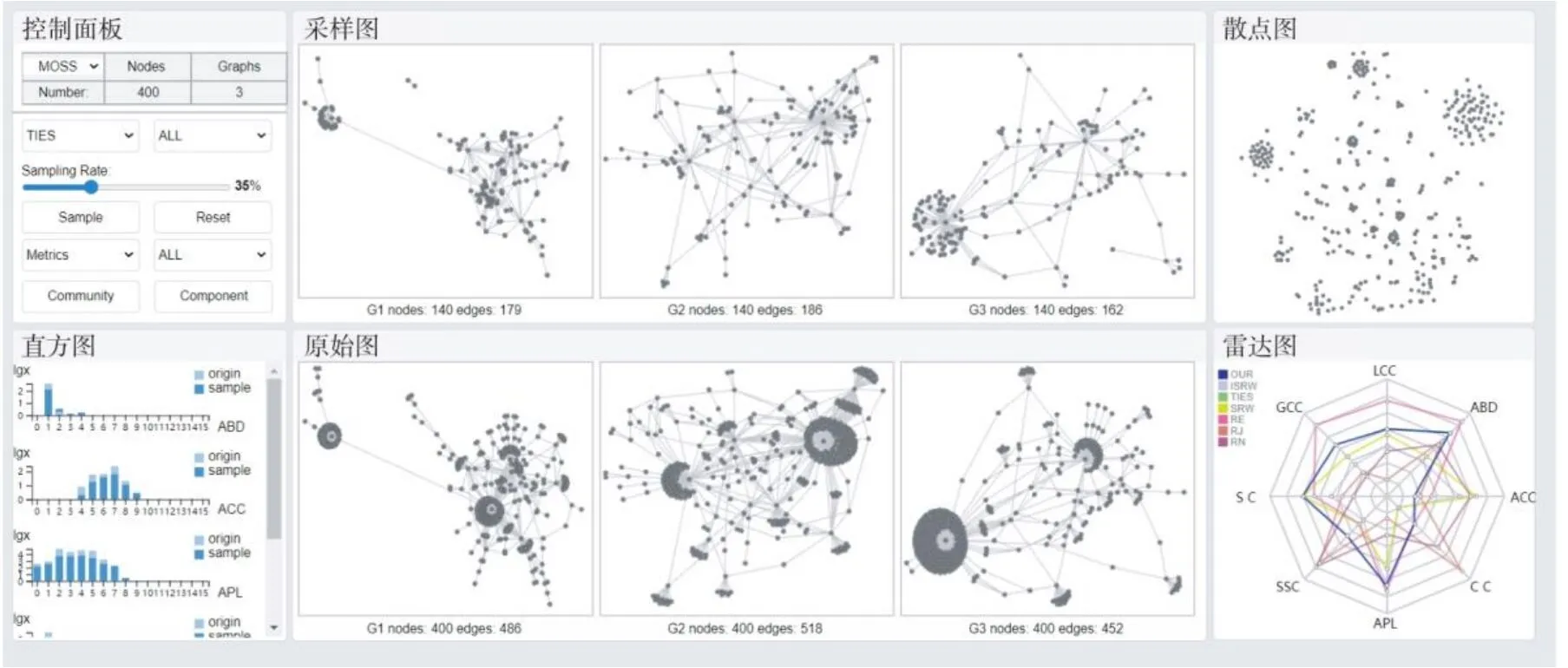
图4 多重网络图采样可视分析系统Fig.4 Visual analytics system of multiple network sampling
3.2 采样算法和评估指标
系统包含3种经典的网络图采样算法。(1)基于节点的采样:本文算法(Our)、随机节点采样(random node,RN)[4];(2)基于边的采样:随机边(random edge,RE)采样[5]、全诱导边(total induction edge,TIE)采样[10];(3)基于游走的采样:简单随机游走(simple random walk,SRW)采样[19]、随机跳转(random jump,RJ)采样[13]、诱导子图随机游走(induced subgraph random walk,ISRW)采样[1]。利用可视分析系统对表1所示的各项指标进行对比。
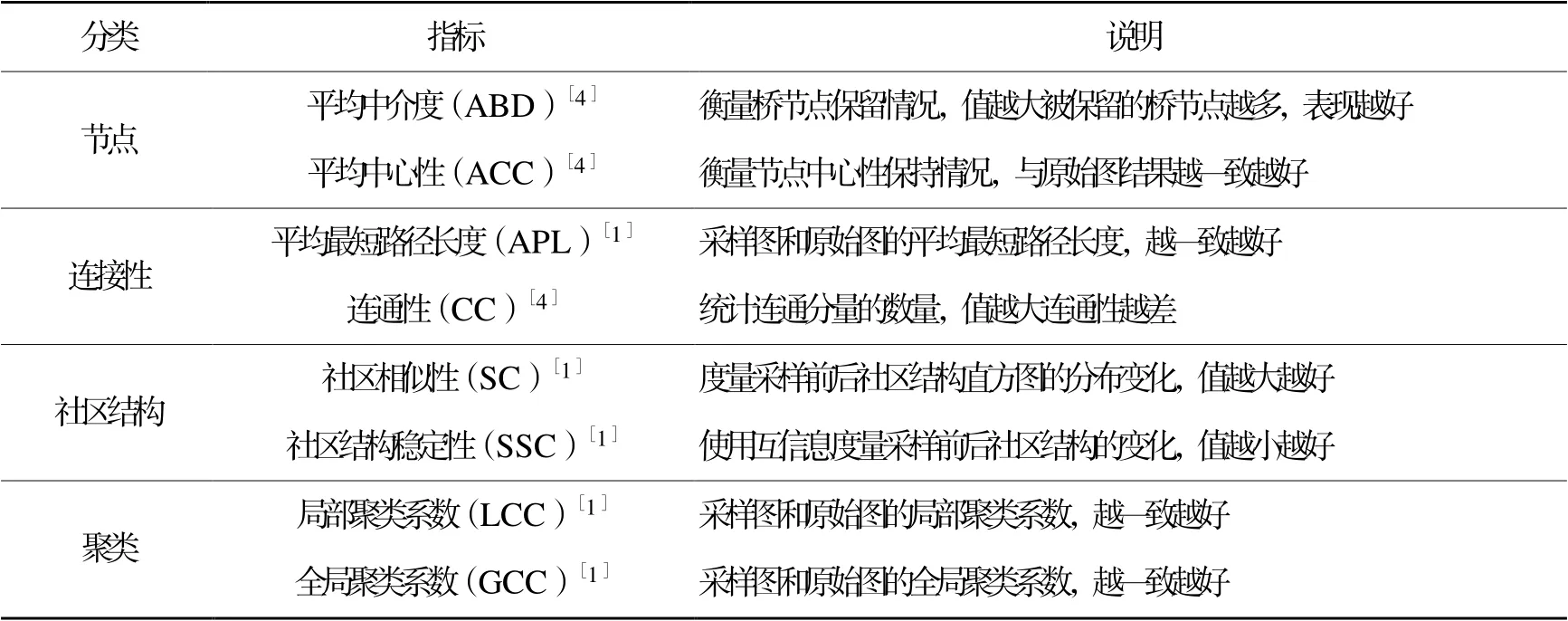
表1 评估指标Table 1 Evaluation metrics
3.3 可视化视图和交互
通过图4左上角的控制面板加载多重网络数据集,选择不同的采样算法并设置采样率等参数完成图采样工作。系统提供以下可视化形式帮助用户交互式地探索采样结果,并评估各类采样算法。
3.3.1 网络视图
图4中间。用点线连接式的图布局展示采样前后的多重网络结构。上方并排展示采样图,下方对应展示每一重网络的原始图。系统还支持节点、社区结构和连通分量的高亮等操作,帮助用户自主选择和探索感兴趣的结构。
图4右上角。利用散点图将表征学习得到的节点向量在二维空间展示,点与点之间的距离表示节点之间的上下文结构相似性,此外,系统还提供了一套交互工具,可支持高亮采样节点、选择感兴趣的局部区域,为探索多重网络上下文结构特征提供便利。
3.3.3 评估视图
(1)图4左下角。以直方图的形式展示采样前后某些结构特征的分布情况,包括节点中介度、节点中心性、最短路径长度、局部聚类系数和社区节点数量。例如,可通过堆叠的直方图清晰直观地观察采样前后节点中介度的分布变化,从而估计采样后是否保留原始图中中介度较高的节点。
(2)图4右下角。以雷达图的形式展示所有采样算法在各项指标上的表现情况。每个径向轴代表一项度量指标,且与同一类别的指标轴相邻,而指标值由内向外表示从小到大。位于雷达图右上方的径向轴为ABD,沿顺时针方向排列的轴依次为ACC,CC,APL,SSC,SC,GCC和LCC,不同颜色的闭合连线代表不同的采样算法,可帮助用户快速对比和评估不同采样算法的有效性。
4 评估
4.1 量化实验
每种采样算法在多重网络数据集上运行20次(采样率设置为10%),统计所有网络图各项指标的平均值。传统的算法是单图采样,因此在每次测试中,随机将其应用于某一重图,并将采样点的结果推广至其他几重图。表2和表3分别为各算法在MOSS数据集和CELE数据集上的评估结果,箭头↑和↓分别表示指标值越大越优和越小越优。
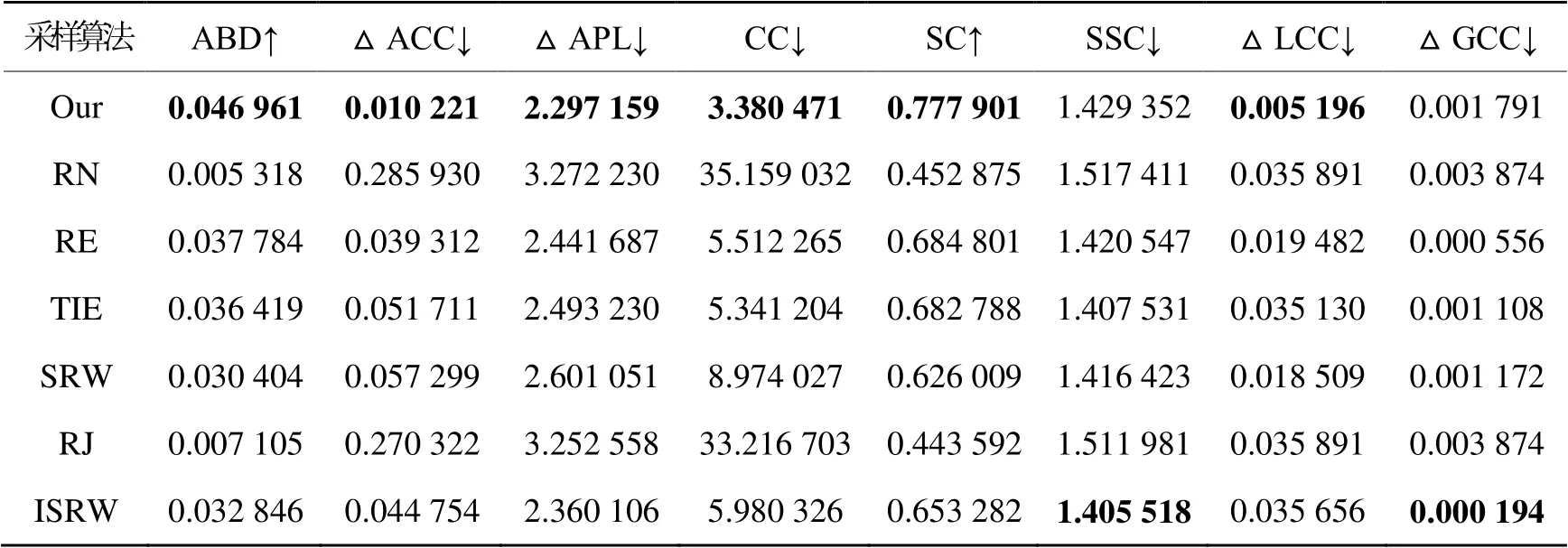
表2 各采样算法在MOSS数据集中的评估结果Table 2 Evaluation results of different sampling algorithm on MOSS dataset
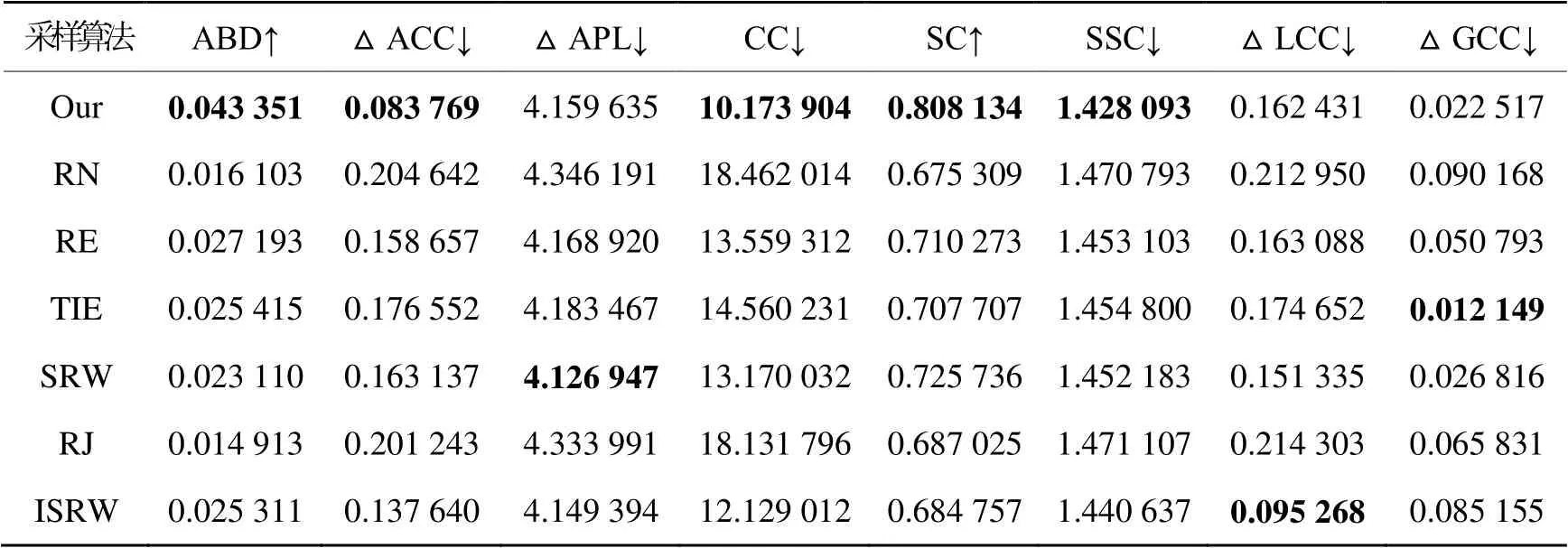
表3 各采样算法在CELE数据集中的评估结果Table 3 Evaluation results of different sampling algorithm on CELE dataset
如表2所示,在MOSS数据集中,本文算法在ABD,ACC,APL,CC,SC和LCC指标上表现最优,ISRW算法在SSC和GCC上最优。如表3所示,在CELE数据集中,本文算法在ABD,ACC,CC和SC指标上依然维持最优;在SSC指标上排名由MOSS数据集中的第5升至第1;虽然在APL和LCC指标上排名有所下滑,但依然排在前3;在GCC指标上排名由MOSS数据集中的第5升至第2。SRW,ISRW和TIE算法分别在APL,LCC和GCC 3项指标上排名第1。
对比MOSS和CELE两套数据集的特点,发现MOSS数据集的节点数量为400,每一重图包含连边的数量均在500左右。而CELE数据集的节点数量为237,但每一重图包含连边的数量均在1 300左右,网络连接关系更为紧密和复杂。由以上量化结果可知,本文算法在面对具有不同结构特点的多重网络数据时,大部分指标更为优秀和稳定,但在某些指标上有所起伏。
分析可知,本文算法注重维持所有网络图的全局结构以及它们之间的关联和互通性,因此当节点连接相对稀疏时(如MOSS数据集),本文算法在APL指标上的优势更明显,但当节点连接普遍紧密时(如CELE数据集),其他算法也能相对较好地保持连通关系,一定程度上弱化了本文算法在该指标上的优势。
此外,本文算法忽略了局部区域之间连接关系的相对强弱,尤其在MOSS数据集中,区域之间的关联强弱变化明显,本文算法在采样后打破了原有节点间的强弱关联关系,从而改变了原有的社区结构稳定性(SSC)和全局聚类系数(GCC)。但在CELE数据集中,节点之间的连接普遍紧实,局部区域之间的连接关系都很强且相对稳定,弥补了本文算法在关系强弱保持上的不足,使得本文算法的这2项指标得到提升。
在实验结果中,只在某1~2项指标上排名第1的ISRW和SRW采样算法,均考虑局部特征,在保持社区结构稳定性和局部聚类系数方面有一定优势。但在更多的全局特征上,如反映重要节点保留的ABD和ACC指标、反映全局社区采样的SC指标和反映连通性的CC指标,本文算法均优于传统的图采样算法,能在更大程度上保留多重网络图的全局特征。
4.2 案例分析
在多重网络图采样可视分析系统中,加载MOSS数据集,将采样率设置为15%。从基于点、边和游走的算法中各选择一种经典的采样算法RN,RE和SRW,将其应用于第一重图,进一步应用于第二和第三重图,得到节点接近中心性分布直方图,如图5所示,从左到右依次为第一、二、三重图的采样结果。在行列相间位置的直方图中,横轴表示节点接近中心性经归一化后的度量值,纵轴表示落在相应区间的节点数量的对数值,从而缩小了柱状图之间的高度差,方便对比。
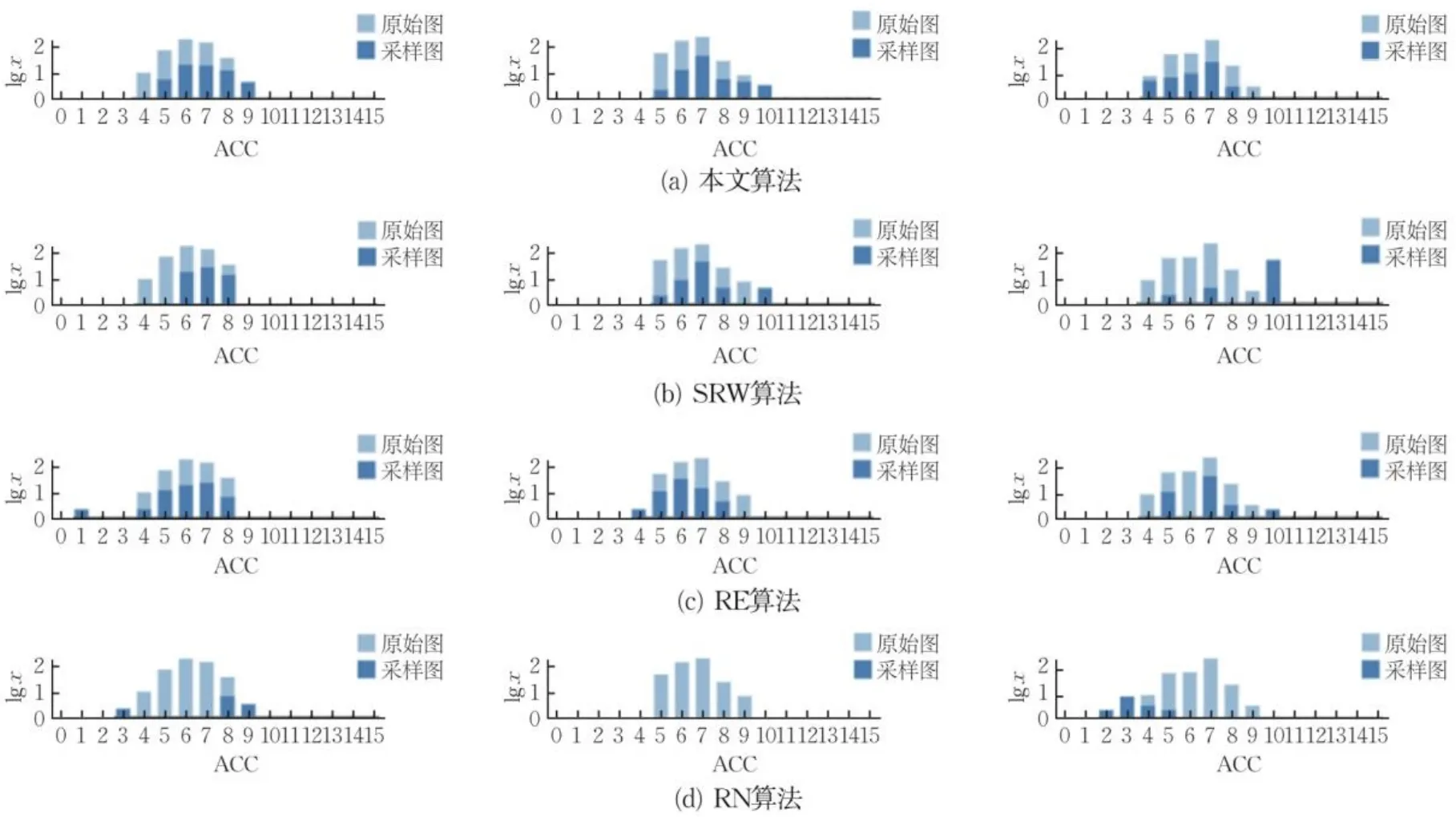
图5 节点接近中心性分布直方图对比(MOSS)Fig.5 Comparison of histogram distributions for node closeness centrality (MOSS)
由图5可知,相较传统算法,本文算法获得的采样结果涵盖原有直方图分布区间的范围较广,且采样柱状图的高度和大小比例与原始图更一致。例如,最后一行的RN采样算法效果最差,在每一重图上的深色柱状图较少,与原始网络图的节点接近中心性分布差异较大。而RE和SRW算法形成的直方图分布连续性较差,在中间某1~2段区间出现了缺失(右侧第三重图最明显),在左侧或右侧的空白区间易产生新的直方图,表现极不稳定。结合量化实验可知,本文算法不仅在节点接近中心性上的宏观统计表现最优,而且在每一重图上均能较好地保持分布特征。
图6为本文算法和在量化实验中表现相对较好的ISRW和TIES算法的对比,其中,(a)为在MOSS数据集中每一重图的力导向布局,(b)(c)和(d)依次为本文、ISRW和TIES算法在15%采样率下得到的可视化效果,(c)和(d)均为将对应算法应用于第一重网络,然后将采样结果推广至其他2重图得到的采样结果。所有结果均按第一、二、三重图的顺序从左到右依次展示,每一重图的节点颜色都映射为在该网络结构下的社区分类。
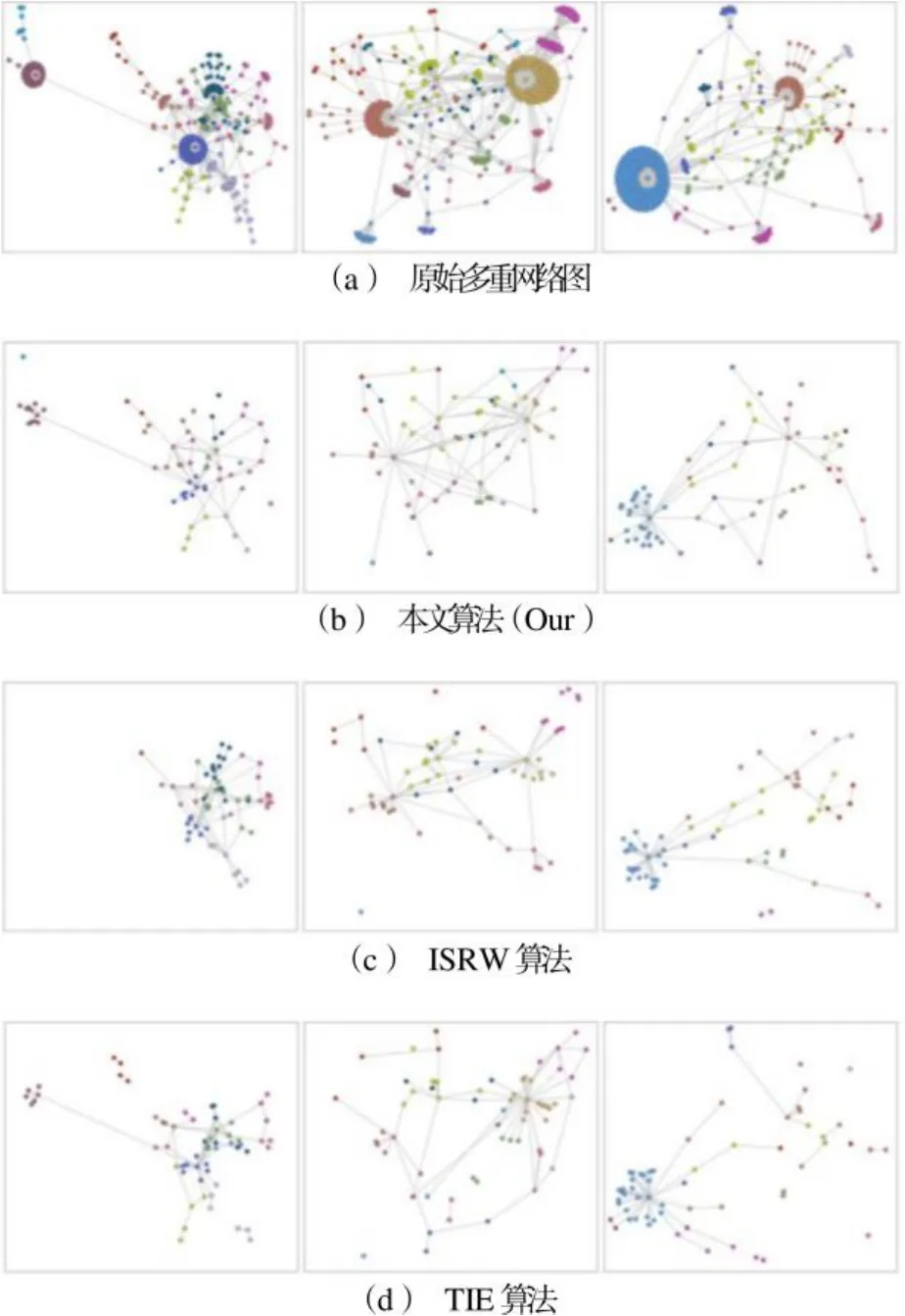
图6 在MOSS数据集中的采样结果可视化对比Fig.6 Comparison of sampling results of MOSS dataset
由图6可知,本文算法在每一重图的区域覆盖和连通性上均表现最优。例如,ISRW算法在第一重图上出现了严重的社区丢失现象。对比图6(a)原始的第一重图,不难发现图6(c)在左上角区域的灰色社区和青色社区中没有采样到任何一个节点,使得用户对全局结构的感知极易出现偏差。图6(d)所示的TIES算法在第二重图的中间出现了明显的空白区域,无法保留一些起关键连通作用的节点和连边。
本文算法使用了综合所有图上下文结构特征的图表征学习方法,并在此空间内使用覆盖性较好的蓝噪声采样算法,使得每一重图的社区或局部区域都有点被采样,从而较为完整地保留了全局结构。此外,图6(c)中的第二、三重图和图6(d)中的第一、三重图均存在较多的孤立点和明显的不连通分量,无法正确推断网络间的区域互联和社区连通情况,而此类问题在图6(b)中出现较少,关联缺失的现象不明显,进一步验证了本文算法在CC和SC这2项指标上表现最优。
最后利用多重网络图采样可视分析系统加载CELE数据集,将采样率设置为20%。选择RJ算法和TIES算法,并将其应用于第三重网络,进一步探索得到的采样结果在每一重图中的连通情况,见图7。其中,(a)展示了原始的多重网络图布局,(b)(c)和(d)依次为本文、RJ和TIES算法的连通分量高亮可视化效果,其中孤立节点用同一种颜色高亮展示,其余的连通分量用不同颜色的包围盒展示。
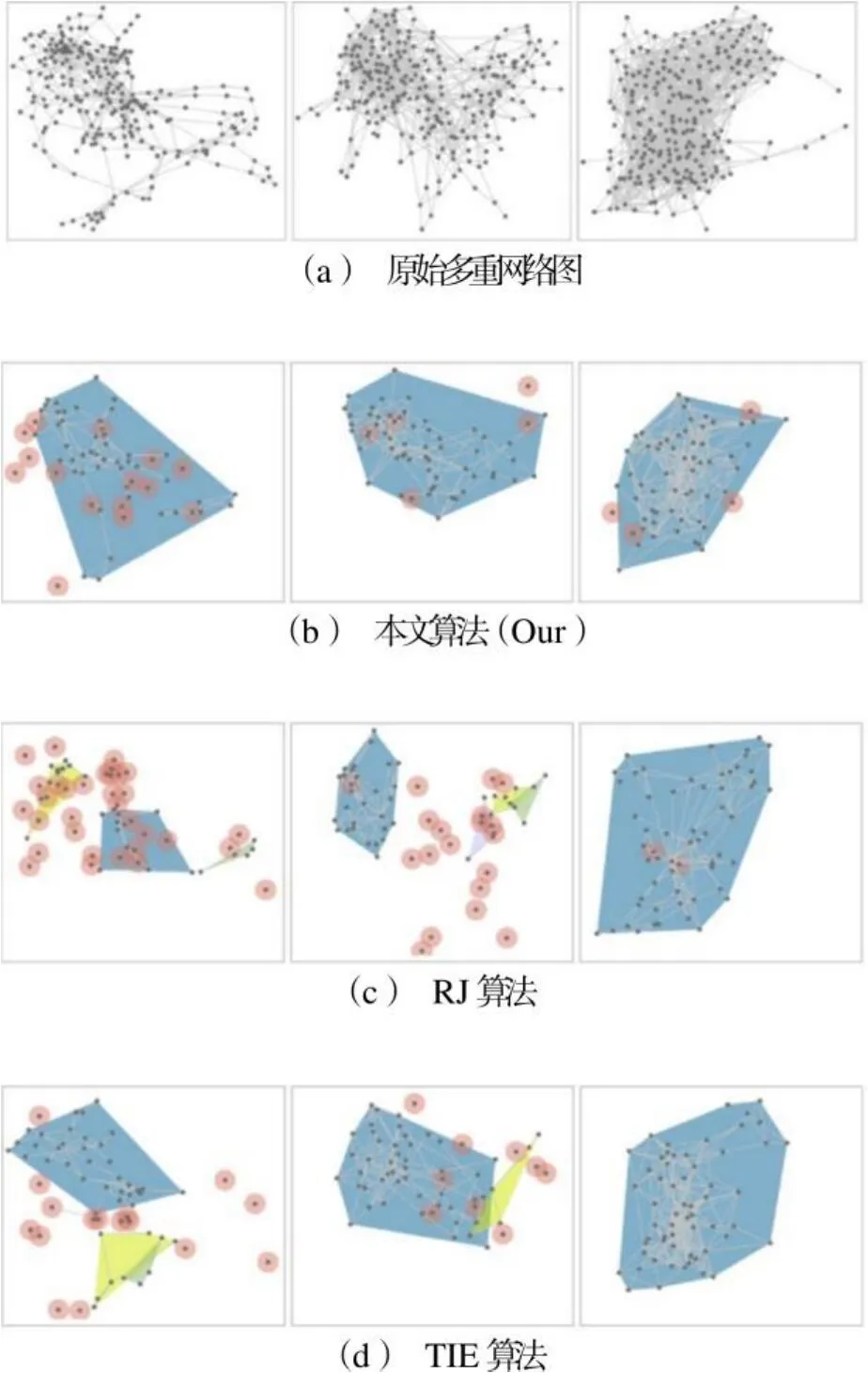
图7 在CELE数据集中的采样结果可视化对比Fig.7 Comparison of sampling results of CELE dataset
由图7(b)知,本文算法在第一重图上表现稍差,出现了10个左右的孤立节点,在第二、三重图上均出现了5个左右的孤立节点,而在每个图中生成的主体连通子图,均能较好地还原初始网络的全局结构和整体特征。相比之下,图7(c)和(d)均在第三重图上表现较好,只有1~2个孤立节点,但在其余2重图上表现较差,除产生10多个孤立节点外,还形成了2~3个规模较大的连通子图,容易破坏用户对网络结构的整体认知。具体原因为RJ和TIES算法均以第三重图为参照进行采样,没有考虑其他重图,因此只有参照图维持了一定的结构特征,无法同时保持多重网络图的结构属性。本文算法能同步保持每一重图的结构关联,因此在多重网络图上的采样表现更稳定。
5 结论
利用改进的自适应蓝噪声采样算法,从多重网络图表征学习空间中启发式地筛选节点,尽可能地实现多重网络图的特征保持。基于多重网络图采样可视分析系统的案例分析和量化实验均显示了本文算法在多重网络图采样中的有效性。下一步将在规模更大、网络图数量更多的多重网络数据集中进行采样效果实验,以分析和测试本文算法的可拓展性。此外,通过与领域专家密切讨论进一步改进多重网络图采样可视分析系统的视图设计和交互功能,提高系统的实用性。
[1]ZHOU Z, SHI C,SHEN X, et al. Context-aware sampling of large networks via graph representation learning[J]. IEEE Transactions on Visualization and Computer Graphics,2020, 27(2):1709-1719. DOI:10.1109/TVCG.2020.3030440
[2]CHENG K. Sampling from large graphs with a reservoir[C]// Proceedings of the 2014 17th International Conference on Network-Based Information Systems. Los Alamitos:IEEE Computer Society Press, 2014:347-354. DOI:10. 1109/NBiS.2014.25
[3]MAGNANI M, ROSSI L. Formation of multiple networks[C]// International Conference on Social Computing, Behavioral-Cultural Modeling and Prediction. Berlin/Heidelberg: Springer,2013: 257-264. DOI:10.1007/978-3-642-37210-0_28
[4]SUN R, ZHANG L,CHEN Z. A sample-based approximate ranking method for large graphs[C]// 2018 6th International Conference on Advanced Cloud and Big Data(CBD). Los Alamitos: IEEE Computer Society Press,2018: 112-117. DOI:10. 1109/CBD.2018.00029
[5]TÜRKOGLU D, TURK A. Edge-based wedge sampling to estimate triangle counts in very large graphs[C]// 2017 IEEE International Conference on Data Mining(ICDM). Los Alamitos: IEEE Computer Society Press,2017: 455-464. DOI:10. 1109/ICDM.2017.55
[6]YOON S H, KIM K N,HONG J, et al. A community-based sampling method using DPL for online social networks[J]. Information Sciences, 2015,306: 53-69. DOI:10.1016/j.ins. 2015.02.014
[7]HU J, HONG S H,CHEN J, et al. Connectivity-based spectral sampling for big complex network visualization[C]// International Conference on Complex Networks and Their Applications. Cham:Springer, 2020:237-248. DOI:10.1007/978-3-030-65347-7_20
[8]ZHOU Z, MENG L,TANG C, et al. Visual abstraction of large scale geospatial origin-destination movement data[J]. IEEE Transactions on Visualization and Computer Graphics,2018, 25(1):43-53. DOI:10.1109/TVCG.2018.2864503
[9]GUO D, ZHU X. Origin-destination flow data smoothing and mapping[J]. IEEE Transactions on Visualization and Computer Graphics,2014, 20(12):2043-2052. DOI:10.1109/TVCG.2014. 2346271
[10]ZHAO Y, JIANG H,CHEN Q, et al. Preserving minority structures in graph sampling[J]. IEEE Transactions on Visualization and Computer Graphics,2020, 27(2):1698-1708. DOI:10.1109/TVCG.2020.3030428
[11]MAIYA A S, BERGER-WOLF T Y. Benefits of bias: Towards better characterization of network sampling[C]// Proceedings of the 17th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York: ACM Press,2011: 105-113. DOI:10.1145/2020408. 2020431
[12]NGUYEN Q H, HONG S H,EADES P, et al. Proxy graph:Visual quality metrics of big graph sampling[J]. IEEE Transactions on Visualization and Computer Graphics, 2017,23(6): 1600-1611. DOI:10.1109/TVCG.2017.2674999
[13]WU Y, CAO N,ARCHAMBAULT D, et al. Evaluation of graph sampling: A visualization perspective[J]. IEEE Transactions on Visualization and Computer Graphics,2016, 23(1):401-410. DOI:10.1109/TVCG.2016.2598867
[14]ZHANG F Y, ZHANG S,WONG P C, et al. A visual evaluation study of graph sampling techniques[J]. Electronic Imaging, 2017,2017(1): 110-117. DOI:10.2352/ISSN.2470-1173.2017.1.VDA-394
[15]ZHANG D, YIN J,ZHU X, et al. Network representation learning: A survey[J]. IEEE Transactions on Big Data, 2020,6(1): 3-28. DOI:10.1109/TBDATA.2018.2850013.
[16]PEROZZI B, AL-RFOU R,SKIENA S. Deepwalk: online learning of social representations[C]// Proceedings of the 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York: ACM Press,2014: 701-710. DOI:10.1145/2623330.2623732
[17]GROVER A, LESKOVEC J. Node2vec:Scalable feature learning for networks[C]// Proceedings of the 22th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York: ACM Press,2016: 855-864. DOI:10.1145/2939672.2939754
[18]WANG Y, CHEN L,JO J, et al. Jointt-SNE for comparable projections of multiple high-dimensional datasets[J]. IEEE Transactions on Visualization and Computer Graphics,2022, 28(1):623-632. DOI:10.1109/TVCG.2021.3114765.
[19]SARMA A D, NANONGKAI D,PANDURANGAN G, et al. Distributed random walks[J]. Journal of the ACM,2013, 60(1):1-31. DOI:10.1145/2432622. 2432624
Representation learning driven multiple graph sampling
YU Ruiqi1, LIU Yuhua1, SHEN Xilong2, ZHAI Ruyu1, ZHANG Xiang2, ZHOU Zhiguang1
(1. School of Media and Design,Hangzhou Dianzi University,Hangzhou310018,China;2. School of Information Management and Artificial Intelligence,Zhejiang University of Finance and Economics,Hangzhou310018,China)
The existing graph sampling techniques pay attention mainly to single graph sampling, focusing on how to preserve the specific topological features of a graph by sampling, such as node degree, cluster coefficient, connectivity. With the improvement of data acquisition capability, multiple graphs, namely a set of nodes exhibits different relationships in different scenarios, have become quietly ubiquitous in the real world. To address this problem, a multiple graph sampling driven by representation learning is proposed. First, a graph representation learning method is designed to fuse the structural features of multiple graphs, through which the nodes are projected into a two-dimensional representation learning space. Then, considering node density and network connectivity, an improved the adaptive blue noise sampling algorithm is employed to select nodes from the representation learning space meanwhile simultaneously preserving the contextual structure features of multiple graphs. Furthermore, an interactive visual analytics system is developed allowing users to explore and analyze multiple graph sampling, and visually compare results with various sampling strategies. Case studies and the experimental results based on two real-world datasets have demonstrated the effectiveness of the proposed method in sampling multiple graphs.
multiple network graphs; graph sampling; visual analysis; evaluation
TP 391.41
A
1008⁃9497(2022)03⁃271⁃09
2022⁃01⁃30.
国家自然科学基金资助项目(61802339,61872314);浙江大学CADamp;CG国家重点实验室开放课题(A2224).
虞瑞麒(2001—),ORCID:https://orcid.org/0000-0001-6116-6678,男,本科生,主要从事数据可视化研究,E-mail:yrq0121@hdu.edu.cn.
通信作者,ORCID:https://orcid.org/0000-0003-0600-4056,E-mail:liuyuhua@hdu.edu.cn.
10.3785/j.issn.1008-9497.2022.03.002
