长程视野下的起点型核心知识教学*
——以“正比例和反比例”的教学为例
2022-06-02刘正松
刘正松
数学知识结构严谨,但鉴于学生认知规律和课时教学需要,教材编写时都进行了较为合理的划分。这样一来,原本结构化的知识便散点式地分布于各年级的教材中,不少教师会平均着力于每个知识点的教学,这是导致学生学业负担过重的原因之一。教师拥有长程视野,聚焦起点型核心知识精准施教,将有助于学生夯实知识结构的根基,进而生发和建构新的知识。“正比例和反比例”便是典型的起点型核心知识。它作为刻画某一现实背景中两种相关联的量的变化规律的数学模型,从常量到变量,是学生认识过程中的一次重大飞跃。虽然学生在过去学习用字母表示数和运算律的过程中,对变量的思想有过一些感知,但真正用函数的观念探索两种相关联的量的变化规律是从“正比例和反比例”开始的。[1]
一、学习检测
为了解“正比例和反比例”这一起点型核心知识的学习现状,我们在一所学校展开教学研究。该校六年级共10个班,369名学生,从中随机选取5个班作为实验班,另外5个班作为对照班。对照班教师按照教材编排,参照苏教版小学数学教材编写组编写的《小学数学备课手册(六年级下册)》中的教学设计展开教学。一周后,我们将两组判断题编制在一张练习中,组织学生随堂练习。
1.根据图1每个表中对应数量之间的关系,判断哪些量成正比例,哪些量成反比例,哪些量既不成正比例也不成反比例。
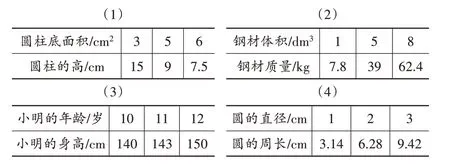
(图1)
2.判断各题的两种量是否成比例,成比例的是成正比例还是成反比例。
(1)100名同学参加团体操表演,每排的人数和排数。
(2)王叔叔每分钟浇树的棵数一定,浇树的时间和浇树总棵数。
(3)正方体的体积一定,底面积和高。
(4)已知xy=10,x和y。
检测结果如表1所示:

表1 “正比例和反比例”对照班检测结果统计表
同为判断两种量是否成正比例或反比例,正确率悬殊较大,我们就练习内容对部分师生进行了访谈,了解他们的真实想法。当问学生“判断第1题表格中的两种量和第2题文字描述的两种量哪个更容易?”时,学生回答:“判断表格中的两种量更容易,因为根据表格中的数据可以很快推算出两种量是比值一定还是乘积一定。”当就“正方体的体积一定,底面积和高”一题问学生“你是怎么想的?”时,学生说出了自己的想法:“因为正方体的底面积乘高等于体积,体积一定,说明底面积和高的乘积一定,所以底面积和高成反比例。”从学生的回答中不难看出,他们的思路很“清晰”。学生真实的想法也便于我们找出问题的症结所在。此外,有两位教师竟然也认为“正方体的体积一定,底面积和高”一题的答案为“反比例”。当我们进一步解释时,两位教师才意识到错误。现实中,部分教师教学时更多关注具体课时的内容,而缺少对教学内容来龙去脉的长程考量,出现问题也是在所难免。
二、教学重构
为了帮助学生精准建构正、反比例的意义,我们重组教材内容,以列表为主要表征方式,将正、反比例的意义融为一课时在实验班展开教学。
1.认识“两种相关联的量”
出示表2至表6。

表2 学生身高与数学成绩统计表
提问:每张表格中的两种量有联系吗?
学生先独立观察、思考,然后集体交流,明确:表2中两种量没有联系,其余四张表中两种量有联系。
揭示:两种相关联的量。
2.认识“正比例”和“反比例”
谈话:刚才大家看到了表中“变化”的量,谁能从“不变”的视角分析一下后四张表?
在学生交流的基础上用数量关系式表示出表中不变的关系。(逐一板书)
追问:回头看看这四张表格,如果让你分分类,你会怎么分?
通过交流,明确:表3和表6一类,表中两种量的积不变;表4和表5一类,表中两种量的商不变。

表3 学生分组组数与每组人数统计表

表4 汽车行驶时间和路程统计表

表5 铅笔的数量和总价统计表

表6 装配计算机的工作效率和工作时间统计表
揭示:正比例和反比例。
3.明确判断方法
出示:正方形的周长和边长成比例吗?成什么比例?
师生合作列表,借助表格数据进行判断。
出示:长方形的面积一定,长与宽成比例吗?成什么比例?
学生独立思考,集体交流判断方法。
追问:怎样判断两种量是否成比例?成什么比例?
指名交流,明确方法:根据题意列表判断。
4.尝试建模
提问:成正、反比例的量在我们身边有很多,你能举出一些例子吗?
学生举例,集体交流。
提问:刚才大家举出了很多成正、反比例的量的例子,你们能不能分别用一道式子概括这些例子?
一周后,我们将对照班学生完成的练习发放给实验班学生完成检测,检测结果如表7所示。由表7可知,实验班各题的正确率均高于对照班,特别是“正方体的体积一定,底面积和高”这一题,实验班的正确率明显提升。无疑,我们的教学重构是成功的。回顾上述教学过程,不难发现:有了表格数据的支撑,学生更为准确地把握了这一知识的本质,在脑海中清晰建构了正比例和反比例的数学模型。
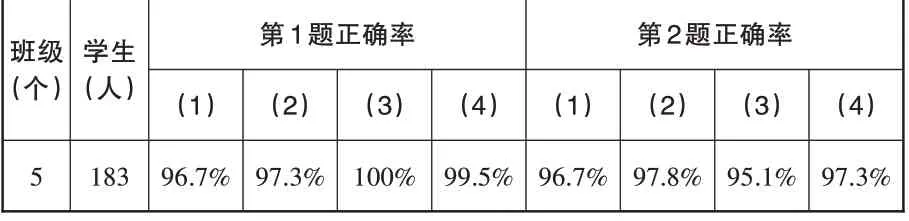
表7 “正比例和反比例”实验班检测结果统计表
三、实施建议
教师作为教育教学活动的主导,应拥有长程视野,对不同领域、板块、序列的核心知识特别是起点型核心知识作出科学的判断和梳理,进而凸显内容本质,细化教学要求,促进学生牢固建构新知。
1.整体研读课程标准
课程标准是教材编写和教师教学的依据,其重要性毋庸置疑。当前,教师大多能准确把握课程性质和基本理念,具体实施教学前也会反复研读学段目标、课程内容和实施建议,这本无可厚非,但数学知识严密的逻辑性使得一个知识点往往只是某一领域、某一板块或某一序列知识的起点、节点或拐点,从中可以生发出一系列新的知识,这就要求我们研读课程标准时不能囿于某一学段,而应贯通各个学段,整体研读。第二学段“正比例和反比例”正是第三学段“函数”的起点。关注第三学段“函数”的课程内容,我们会进一步发现对应关系是函数的核心,表征这种对应关系常用的方式有列表、图像和解析式。对“正比例和反比例”的学习而言,多种表征方式可以清晰呈现概念的形成过程,促进学生理解概念,但不同学段采用的表征方式侧重点应略有不同。就第二学段学生而言,借助列表的方式判断成正、反比例的量,能使抽象的知识更加具体直观,从而丰富学生对正、反比例意义的认识与体验。
2.全面厘清教材意图
教材为学生的学习活动提供了学习主题、基本线索和知识结构,只有全面厘清教材编写意图,才能精准实施课堂教学。苏教版、人教版和北师大版小学数学教材都将“正比例和反比例”安排在六年级下册教学。其中,人教版教材将“比例”与“正比例和反比例”的内容整合为“比例”这一个单元。显然,这更能凸显知识之间的联系。就“正比例和反比例”相关知识的编排而言,人教版与苏教版教材的编排方式较为相似。而北师大版教材在正式学习正、反比例之前特意安排了“变化的量”这一内容,设计三个具体情境,让学生体会变量和变量之间相互依存的关系,并尝试描述这些关系。值得关注的是,三版教材在编排“正比例和反比例”时都结合具体情境借助表格呈现数据,有的表格完整呈现数据,有的表格没有出示全部数据,需要学生在观察、思考的基础上继续填写完整,这正给了学生思考、体验成正、反比例的两个量之间变化关系的空间。如此编排,凸显了正、反比例概念形成与应用的过程与方法,有助于学生进一步弄清正、反比例概念的内涵和外延,而这些都建立在教师全面厘清教材编写意图的基础之上。
3.通盘紧扣教学主线
起点型核心知识具有生长基因,它在学生知识体系建构过程中具有独特价值。因此,教师应通盘紧扣教学主线,让学生获得正确的知识、有效的方法、合理的策略,以保证在后续教与学的过程中能够顺利建构新知识。[2]在现实中,有许多数量关系可以表示为成正比例的量和成反比例的量,其本质是两个量按一定的比例关系发生变化。因此,联系和变化应成为“正比例和反比例”教学的主线。从对照班学生的访谈中不难想到,当前很多教学都注重知识的形式,而忽略知识的本质,当学生想到“正方体的体积=底面积×高”这一数量关系后,他们便将目光聚焦于“积是否一定”上,而在无形中忽略了判断成正、反比例的量的重要前提——变量。因此,教学中结合具体的例子让学生感知两个量的“联系”和“变化”,并在“变量”中找到“不变量”尤为关键。根据小学生的认知发展规律,他们的形象思维更占优势,教学中可以始终借助列表的方式引导他们建构相关概念,后续应用时也可以引导他们通过表格展开说理。这看似有些“朴素”的方法恰能最直观地体现成正比例或反比例的两个量之间的联系与变化,从而促进学生把感性认识上升为理性认识,获得对正比例意义和反比例意义的正确理解。
总而言之,知识是人的素养形成和发展的载体,知识和知识教学要服务于人的素养的形成和发展。[3]因此,基于长程视野,合理地选择和确定教学内容,凸显对学生知识体系建构、核心素养培育具有重要作用的起点型核心知识教学就显得尤为迫切和必要。
