基于深度学习和PnP 模型的激光跟踪仪自动姿态测量

周道德，高豆豆，董登峰*，周维虎，崔成君

（1.中国科学院 微电子研究所，北京 100029；2.中国科学院大学，北京 100049）

1 引言

随着制造业的快速发展，在航空航天、汽车装配等领域，大尺寸高精度姿态测量技术越来越重要。六自由度激光跟踪仪是一种能够快速高精度完成姿态测量的精密仪器，具有测量精度高、测量速度快和测量范围广等优势，在高端制造业和科学工程领域有着广泛的应用需求［1］。目前，商用六自由度激光跟踪仪均为API、Leica、FARO 等外国公司的产品。我国对于激光跟踪六自由度测量的研究较少，华中科技大学、上海交通大学、天津大学等基于盾构机的工作场景，对六自由度测量进行了研究［2］，利用全站仪以及角锥棱镜完成三维位置信息的采集，利用CCD相机以及倾角仪完成姿态测量，但受到倾角传感器的影响，具有测量范围有限、响应速度较低等问题。为了使自主研发的三自由度激光跟踪仪具备六自由度测量能力，本文提出一种面向激光跟踪仪的视觉姿态自动测量方法，其基本思路是在激光跟踪仪上增装单目相机，在跟踪仪测量靶标上增加三维视觉标识，从而在激光跟踪仪测得被测工件三维坐标的基础上，实现对被测件空间姿态的测量。

目前，主流方法使用单目相机来完成视觉位姿（即位置和姿态）的测量［3］。单目视觉位姿测量主要包括以下两种方法：（1）利用深度网络直接回归出位姿参数，6D-VNet［4］、SSD6D［5］等直接回归法缺乏显式的几何约束关系，精度较低［6］，这种方法实际是解决图像检索任务，因此回归出的位姿参数精度仍然受限于图像检索精度［7］；（2）基于3D-2D 特征点的PnP（Perspective-n-Point）位姿估计方法，该方法将位姿求解作为一个几何问题进行优化，精度较高，是目前的研究热点［8］。当3D-2D 点之间的对应关系未知时，PnP 退化为盲PnP 问题［9］（Blind-PnP，BPnP），传统的单目视觉算法通过人工匹配特征点再利用PnP 方法完成位姿求解。得益于深度学习的快速发展，一些工作利用深度网络强大的学习能力获得2D-3D 特征点的对应关系后再利用PnP 模型求解位姿［9-11］。但PnP 位姿求解作为一个几何优化过程，其不可微性导致无法集成在深度网络中，即其高精度的位姿求解能力无法指导网络训练。为了在一个端到端网络中同时实现深度网络的学习和几何算法的优化，DSAC［12］方法利用中心差分来计算PnP 求解过程的偏导数，对于n维输入，需要求解2n次完整的PnP 过程，才能获得完整的雅克比矩阵；DBPnP［13］网络利用声明层理论实现PnP 位姿求解过程对网络训练的指导，但需要耗费较多的资源计算多个二阶偏导数矩阵的逆，且存在运算不稳定的问题。

综合考虑激光跟踪仪对姿态测量精度、速度以及自动化测量的要求，本文提出一种深度学习与经典PnP 模型相结合的姿态测量方法，对单目相机采集到的跟踪仪靶标图像进行预处理得到2D 特征点坐标，使用靶标上预设特征点的3D 坐标以及图像中2D 特征点坐标直接实现姿态的自动测量，对国内现阶段激光跟踪仪的姿态测量需求具有重要的参考价值。

2 基于深度学习的姿态测量方法

本文结合深度学习以及PnP 模型对激光跟踪仪靶标进行姿态测量。整个测量系统主要由激光跟踪仪、相机和靶标组成，目标是求解靶标坐标系Ot相对于相机坐标系Oc之间的旋转矩阵（也可以表示为航天航海领域常用的RPY 角形式，定义x轴对应俯仰角、y轴对应偏航角、z轴对应横滚角），其示意图如图1 所示。在对相机拍摄的图像进行预处理得到2D 特征点坐标后，可以直接使用姿态测量网络结构进行姿态求解，姿态测量网络的解算流程如图2 所示。

图1 激光跟踪姿态测量系统示意图Fig.1 Schematic diagram of laser tracking attitude measurement system

图2 姿态解算流程Fig.2 Flow chart of attitude solution

该姿态测量网络的解算过程主要分为特征提取、特征点匹配和姿态求解3 个步骤。首先，通过特征提取以及特征点匹配两部分结合确定PnP 模型求解姿态时所需的特征点匹配关系；在姿态求解时，利用已确定的特征点匹配关系以及已知的坐标信息结合PnP 模型完成高精度的姿态解算。假设已经对相机图像预处理得到了2D特征点坐标，且3D 特征点坐标已知。

2.1 特征提取

在激光跟踪仪的工作场景下，特征点之间的对应关系往往是未知的，是一种典型的BPnP 问题，无法直接使用PnP 模型进行姿态求解，直接对原始特征点进行匹配相当困难。由于深度学习在提取数据隐含的特征时体现了无与伦比的强大潜力，为了实现特征点的自动匹配，本文使用深度学习的方式，首先提取输入特征点有区分性的特征以便完成后续的特征点匹配。网络的原始输入为2D 和3D 特征点的坐标，输入（2D 特征点和3D 特征点）首先通过一个预卷积层调整为相同的维度后，使用由8 个残差块（ResBlock）跨层连接组成的特征提取网络对2D 特征点和3D 特征点进行特征提取，特征提取网络如图3所示。

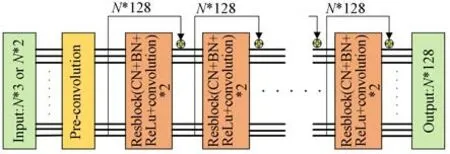
图3 特征提取网络Fig.3 Feature extraction network

激光跟踪仪工作过程中，随着靶标位姿的改变，图像中的2D 特征点分布会发生剧烈变化。为了提取到具有强不变性的特征，本文在提取单个输入点的特征时利用上下文归一化［14］（Context Normalization，CN）操作将全局信息加入到特征提取网络中，通过特征向量的分布对特征进行归一化，从而指导每个点的特征提取。具体来说，每个残差块中分别包含两个卷积层以及两次上下文归一化和两次批次归一化操作（Batch Normalization，BN），使用ReLU 函数作为残差块中每个神经元的激活函数。将第i个样本在第l层的输出向量记为，第l层的均值向量和标准差分别为：

本文对特征提取网络进行了改进：（1）采用预激活策略，在每个残差块内部先进行CN、BN操作和ReLU 函数激活，卷积层放在激活函数之后，消除了残差块非负输出对特征提取的影响，提升了特征提取网络的性能；（2）针对激光跟踪仪姿态测量时靶标坐标系固定的特点，去掉了3D 点特征提取前常用的规范化操作，和改进前的网络相比，网络的参数量下降了约30%，在不影响效果的前提下使模型更适合部署到激光跟踪仪的生产环境中。最后，得到第i个特征点的128 维特征向量：记为zi∈R128。

2.2 特征点匹配

基于PnP 模型的高精度位姿求解需要确定特征点之间的匹配关系，本文利用具有强不变性的高维特征，将特征点匹配作为一个优化问题，通过优化求解特征向量之间的最优传输问题得到特征向量之间的匹配概率，从而完成特征点匹配。

定义3D，2D 特征点的特征向量之间的距离为：

基于定义的向量间距离，对所有2D-3D 特征点对应的特征向量形成距离矩阵D，熵正则项平滑后的特征点匹配的最优传输问题可以写为：

其中：＜，＞表示两个矩阵对应元素的乘积和，ε为正则化系数，H(P)表示匹配概率矩阵P的熵。通过Sinkhorn 算法［15］求解式（5），最终该优化过程得到的最优联合概率矩阵P*即为3D-2D 特征点之间的匹配概率矩阵。从P*中选取概率最高的N个元素，可以获得N组3D-2D 点的匹配关系，利用该N组点即可进行后续的姿态求解。

2.3 基于隐式微分的可微姿态解算

利用2D-3D 特征点的匹配关系，在求解姿态时，首先使用基于随机一致性抽样（Random Sample Consensus，RANSAC）的P3P 算法滤除异常匹配点，然后使用EPnP［16］算法解算目标的姿态信息。但该求解过程是一个不可微的几何优化过程，无法显式解析计算每一步梯度，这会导致PnP 模型高精度位姿求解能力无法指导网络训练。为了将PnP 位姿求解过程纳入整个网络的学习过程，提高网络对姿态的解算精度，本文采用隐式微分理论［17］完成位姿求解过程的梯度计算。对于整个位姿求解过程，将目标函数定义为重投影误差函数，即：

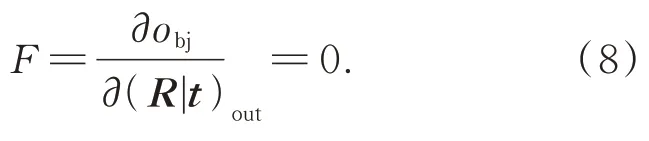
将重投影误差函数obj对输出(R|t)的一阶偏导作为约束F，则位姿求解过程s对输入i的雅可比矩阵可以写为：

式（9）中，不涉及任何位姿求解的中间过程，直接得到了整个过程的雅克比矩阵。对于位姿求解的任何一个输入量，其梯度都可以通过位姿求解层继续反向传播，梯度计算与求解过程中任意的不可微过程无关，从而将该求解过程和之前的特征提取、匹配过程集合在一个深度网络中，实现优势互补。

2.4 损失函数

位置和姿态在PnP 模型求解过程中是同时解出的两个耦合量，因此在整个姿态求解过程中，网络有两个预测对象：特征点之间的匹配以及最终位姿。本文综合考虑了两个预测对象对网络训练的影响，采用双损失函数对网络训练进行监督。即：

式中Lc，Lpose分别对应特征点匹配以及位姿求解任务的损失。衡量匹配结果的损失项Lc表示为：

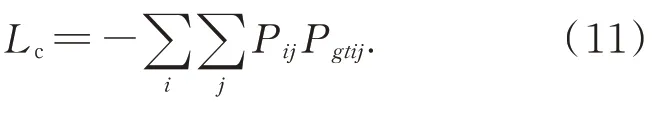
对于位姿损失项，本文对比了多种不同形式的损失函数，包括重投影误差、加权重投影误差和旋转矩阵角度差等。其中，旋转矩阵角度差作为损失函数的结果稍好于其他函数，因此本文采用的位姿损失函数为：

其中P，Pgt，R，Rgt，t，tgt分别表示概率矩阵、旋转矩阵、平移矢量的解算值和真值。

由于使用了可微姿态求解模块，该损失项可以直接用来指导网络训练，该损失项训练模型直接验证了可微姿态求解层的有效性。

3 数据集建立与网络训练

数据集对深度学习起到至关重要的作用，带有位姿信息的大型公开数据集例如Kitti、YCBVideo 等基本利用人工标注的方法提供真实场景下的位姿标签，数据量较小，且容易受传感器标定精度等问题导致错误标注，不适用于激光跟踪仪的高精度测量领域。因此，本文根据激光跟踪仪大范围高精度姿态测量的要求，基于激光跟踪仪靶标上的特征点坐标，制作了一个具有丰富标注信息的数据集。

3.1 数据集制作

对于激光跟踪仪的姿态测量问题，数据集中应该包括相对位姿(R|t)，相机内参K，2D-3D 特征点坐标及点之间的对应关系。由于实采数据并进行标注制作数据集的成本过高且无法保证标注信息的精度，数据集制作采用了更高效的方法，基于相机成像数学模型，利用靶标特征点的空间3D 坐标，通过改变外参获得大量3D-2D 点对以及它们所对应的位姿以及2D 特征点坐标，此处2D 点坐标为消除内参影响的归一化坐标（即假设内参固定）。这一设定可以使模型对任意输入求解时内参固定为单位阵，只需对实际数据输入的像素坐标进行简单的预处理。

该方法降低了数据集制作的难度且保证了标注的精度，和实际拍摄图像制作数据集的方法相比，虽然没有考虑真实场景中可能存在的噪声干扰，但由于模型本身具有一定的泛化能力，在实际场景硬件误差得到较好控制的情况下，通过该数据集训练的网络可以获得准确的姿态解算结果。数据集中样本外参取值为激光跟踪仪的工作范围，即偏航角和俯仰角为±30°，横滚角为±180°，距离为0～30 m 考虑到相机在跟踪仪工作范围内拍摄图像时特征点不会相互遮挡以及后续姿态解算的稳定性等因素，激光跟踪仪的测量靶标上采用非对称非共面布局的14个红外LED作为特征点，LED特征点的分布情况如图4所示。

图4 激光跟踪仪靶标Fig.4 Laser tracker target

针对待测靶标，在测量范围内随机取值，生成了训练集以及测试集。为了模拟真实情况，分别生成了与训练集分布不同的理想测试集，以及在理想测试集中每一个2D 像素特征点上附加一个服从正态分布的随机量的噪声测试集，两测试集中均包含5 324 组测试样本且保证与训练集分布不同。

3.2 网络训练

训练过程基于Pytorch 框架，使用Adam 优化器，Adam 的两个指数衰减超参数设置为0.9，0.999，学习率动态衰减，初始值为0.001 25，batch-size 设置为256。训练过程在Linux 系统下，使用单块RTX3090GPU，训练完成后，在两组测试样本上验证网络性能，测试集中所有样本均为在测量范围内生成的随机样本且保证其分布与训练集不同。

青椒叶片小，蒸腾量小，一般在坐果前不需浇大水，出现干旱时可浇小水。每次浇水要在晴天上午浇，提高棚内温度，中午将潮气放出，避免棚内湿度过大造成病害流行。底肥施足后，坐果前不用追肥，防止徒长，造成“三落”现象。

4 测试集结果分析

根据激光跟踪仪的测量需要，本文使用RPY角的形式对姿态解算结果进行展示，并利用姿态角的测量值与真实角度值θgt的差作为对网络解算值的评价指标，即：

选择RANSAC 和SoftPosit 算法在测试集上与网络进行对比。SoftPosit 算法是BPnP 问题的一种迭代求解方法，可以根据给定的初始值同时完成特征点的匹配以及姿态求解。考虑到实际应用中初始值获取困难，本文选择与真实值相差5°以及相差22.5°的两种初值进行迭代求解。RACSAC 算法作为一种鲁棒的位姿估计算法，在特征点存在误匹配时可以有效地滤除异常点，测试中设置输入RANSAC 算法进行求解的数据中50%的点存在错误的匹配关系。

为了反映测试集上的整体情况，定义姿态误差小于e的样本数占所有样本的比例为r，并绘制了测试集的e-r曲线，如图5 所示。其中，Sp5 和Sp22.5 分别表示不同初值的Softposit 算法，RANSAC 表示用RANSAC 算法直接求解。在数据集上进行消融实验，图5 中Losst表示完整网络结构的测试集结果，Lossc代表不使用2.3 节介绍的可微PnP 求解模块的测试集结果。需要说明的是，如果在特征提取网络中，不使用上下文归一化操作（CN），会使网络难以训练（loss 不收敛），该情况下的e-r曲线基本和x轴重合，因此在图6 中没有画出该条曲线进行对比。但基于上下文信息对特征提取网络进行改进后，网络会提取到更有效的特征，大大提高特征点匹配的准确性以及最终解算出的姿态精度。

图5 测试集的姿态测量结果Fig.5 Attitude measurement results of testset

4.1 理想测试集

理想测试集的结果如表1 所示。在提供较好的先验信息的情况下，直接使用RANSAC 算法处理BPnP 问题耗时15 ms，但结果很差；Soft-Posit 算法平均耗时220 ms，运行收敛到全局最优时，姿态角误差较小，但该算法的平均误差以及均方根误差均大于本方法，且该迭代算法对初始值很敏感；本文方法单次求解耗时约40 ms，解算精度最高，性能最优，能够满足激光跟踪仪的要求。

表1 三种算法的姿态测量结果Tab. 1 Attitude measurement results of three algorithms

图6 利用网络的位姿解算值对理想测试集中随机两个样本的重投影误差进行可视化，3D 特征点的投影点与2D 特征点基本重合，证明解算出的位姿参数精度较高。

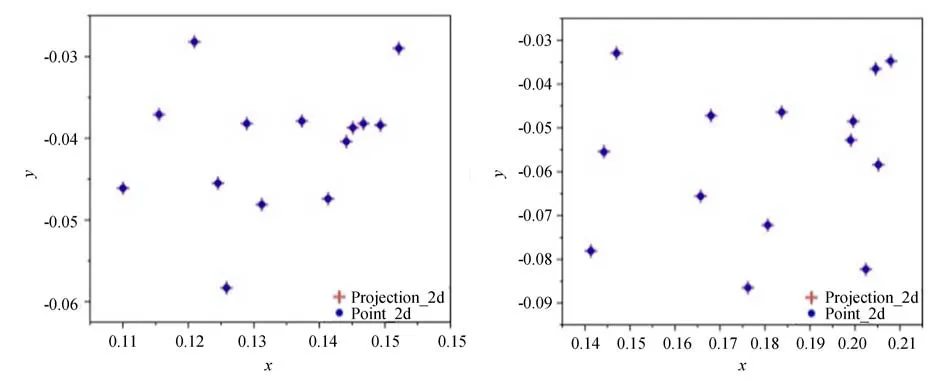
图6 随机两组样本的重投影误差可视化Fig.6 Visualization of reprojection errors for two random samples

4.2 噪声测试集

在实际应用场景中，相机标定以及特征点坐标的获取都会因外界条件干扰而产生误差。为了模拟真实情况，在噪声测试集上额外进行了一组对比，该测试集仿照真实情景，对每一个2D 特征点坐标附加一个符合正态分布的噪声，结果如表1 所示。由表1 可知，姿态解算精度受特征点坐标提取的影响较大；俯仰角和偏航角比横滚角更容易受误差的影响；俯仰角和偏航角的求解精度相当且小于横滚角精度。结合4.1 节的分析可知，当存在噪声时，本方法的精度和速度仍然优于对比算法。

5 实 验

本文搭建的姿态测量实验平台如图7 所示。首先，将相机架设在自主开发的三自由度激光跟踪仪上，对跟踪仪配套的测量靶标进行姿态测量。由于激光跟踪仪实际应用的场景通常比较复杂，为了使相机具有较好的图像稳定性以及强抗干扰能力，以高分辨率和高采样速率为前提，选用DELSA 公司生产的高速工业相机，其分辨率为2 432×2 048，像元尺寸为3.45 μm。

图7 姿态测量系统实验平台Fig.7 Experimental platform of attitude measurement system

将靶标安装在高精度转台上，该二轴转台的俯仰角定位误差小于2.8″，横滚角定位误差小于7.9″，跟踪仪和转台之间的距离为3 m。跟踪仪保证靶标保持在相机视场的中心，高速相机可以在转台转动时采集到清晰的图像用于姿态解算。通过电脑控制转台转动带动靶标运动，使用转台的转动值为标准值，与测量值进行对比，确定测量精度。测量过程中，首先对相机采集图像进行腐蚀、膨胀、滤波、二值化和质心提取等预处理得到2D 特征点坐标，如图8 所示。

图8 图像预处理过程Fig.8 Image preprocessing process

由于高速相机图像的采集速度大于姿态解算速度，因此制约系统测量速度的主要因素是姿态的解算时间（约40 ms）。在该用时下，系统基本能够对靶标的不同转动速度进行实时响应，满足跟踪仪的动态测量要求。

对图像预处理得到的2D 特征点坐标使用相机内参矩阵进行处理后，配合靶标上3D 特征点坐标即可求解姿态。在姿态测量实验中，由于转台只能绕两轴旋转（俯仰角、横滚角），无法进行偏航角的测量实验。为了保证高精度二轴转台转动时姿态解算值不受偏航角分量的干扰，测量之前使两坐标系之间的3 个姿态角尽可能为0°。具体来说，手动完成特征点匹配并利用EPnP 算法确定两坐标系之间较准确的位姿初始值，然后将该初始值放入SoftPosit 算法中运行至收敛，从而确定两坐标系之间的3 个姿态角。根据解算结果对转台以及跟踪仪进行精密调节，从而将初始的3 个姿态角控制在10-4°左右，基本消除了偏航角分量的影响。

转台实际转动的角度与网络解算出的角度如表2 和表3 所示。由于转台只能绕两轴旋转，因此表中数据是俯仰角以及横滚角的实验结果，缺少偏航角的相关数据。由表可知，在3 m处，±30°内本方法最终解算出的俯仰角误差优于0.31°，横滚角误差优于0.03°。

表2 俯仰角实验结果Tab. 2 Experimental results of pitch （°）

表3 横滚角的实验结果Tab. 3 Experimental results of roll （°）

目前，面向激光跟踪设备的高精度姿态测量方法包括基于位置敏感器的姿态测量方法［18］、基于传统单目视觉的测量方法［19］以及利用两者冗余信息进行融合优化的方法［20］等。这些方法和本文提出方法的实验条件以及实验结果对比如表4 所示。

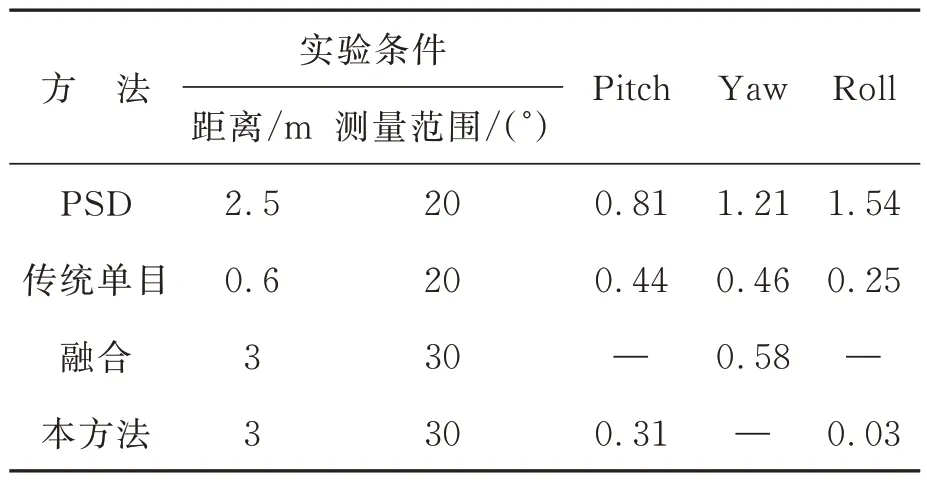
表4 不同方法测量姿态的实验结果对比Tab. 4 Comparison of experimental results of attitude with different methods

由于实验条件的不同，表4 中有部分姿态实验数据在文献中没有给出，但根据本文的仿真结果，本方法对于俯仰角和偏航角具有近似的解算精度，且该精度低于横滚角的解算精度，因此本文方法的姿态角解算精度优于其他方案。

6 结论

为了使自主研发的三自由度激光跟踪仪具备六自由度的测量能力，本文研究并设计了一个姿态自动测量网络。该网络结合了深度学习特征匹配能力与几何PnP 位姿求解算法的优势，实现了姿态的快速高精度解算。基于二维高精度转台的姿态测量实验表明，该方法的横滚角解算误差小于0.03°，俯仰角误差小于0.31°，解算时间约为40 ms，具有较好的测量精度以及实时性，相比于目前已有的姿态测量方法，速度和精度均有所提升，且可以实现姿态的自动测量，对实现激光跟踪仪的姿态快速测量具有重要参考价值。通过在3 m 处进行测量实验验证了本方法的性能，但考虑到不同距离下特征点坐标的精度会影响最终的姿态解算精度，未来的工作将从靶标特征点的布局、红外LED 选型以及相机标定、图像预处理算法等方面进行改进，进一步提高本方法的姿态测量精度。