基于Matlab GUI移动衰落信道的仿真研究
2022-06-01谢文娣王恩亮
谢文娣,王恩亮
(安徽新华学院 电子工程学院,安徽 合肥 230088)
0 引 言
通信的目的是传递信息,而任何信息都必须经过信道进行传输.信道即信号传输经过且由各种传输媒质构成的通道.信道质量的优劣关乎通信系统中信号的接收和还原,恶劣的信道会给信息的传输带来各种弊端.由于通信应用场的持续扩展和信道环境的复杂性,从而导致信号传播的多样性,信道便不能用准确的模型来描述,同时衰落也是影响移动信道性能的关键要素.因此为减少衰落进一步提高通信性能,必须深入研究移动衰落信道特性并构建相应的信道模型.然而移动衰落信道知识比较抽象,理论性强,涉及数学公式繁多且复杂,传统纯理论分析教学法枯燥乏味,学者难以理解和掌握.针对上述问题,本文利用Matlab软件借助GUI工具设计一个移动衰落信道仿真系统,界面友好,直观形象,可视化程度高,为通信系统研究者特别是相关专业的学者理解和掌握信道衰落和信道传输特性提供帮助[1-4].
1 移动衰落信道特性与模型
1.1 移动衰落信道特性
移动信道与传播环境被限定的有线信道不同,它随时间发生变化,无线传播环境中所有影响电磁波传播如地貌、建筑、树木、车辆等因素都将制约着信道的质量.在传输过程中存在许多固定或移动的障碍物,同时因无线通信的收发两端用户的自由移动,信号传播时常常出现反射、散射和衍射现象,因此移动信道的主要特点是多径传播和“衰落”,无线传播示意图如图1所示.多径传播是因为发射端和接收端之间的复杂环境从而引起电磁波沿多条路径传输最终到达目的地;衰落是由于信道的变化导致接收信号出现强弱变化的现象,它有小尺度和大尺度衰落之分,具体分层结构如图2所示[5].

图1 无线传播示意图

图2 衰落的分类
小尺度衰落是指无线信号在经过短时间或短距离传播后其幅度、相位或多径时延产生的快速变化,它往往是由多径效应和多普勒频移一起影响形成的,如多径衰落.大尺度衰落是由移动通信信道路径上固定障碍物的阴影引起的信号功率减弱现象,如阴影衰落[6-7].小尺度衰落是无线信道衰落的关键所在,所以本文主要研究小尺度衰落信道传输特性.
1.2 移动衰落信道模型
常见的小尺度衰落信道模型主要有瑞利衰落模型、莱斯衰落模型以及Nakagami-m模型三种.
瑞利(Rayleigh)信道模型是无线信道建模中最基础的模型.在多径传播信道中,信号经过多条传输路径到达接收端且各路径的时延不一样,使得合成信号的包络服从瑞利分布,所以这种衰落称为瑞利衰落,它是一种特殊的多径衰落,其相位服从均匀分布[8].小尺度衰落服从瑞利分布的概率密度函数如(1)式所示,相位服从均匀分布如 (2) 式所示.
(1)
(2)
如果接收端中既有散射路径的信号,信道中又存在固射分量,即以直射波为主导,这种衰落称为莱斯衰落.当分量很小时,近似为瑞利衰落.莱斯分布的概率密度函数如(3)式所示.
(3)
Nakagami-m分布为长距离、宽频带信道普遍应用的模型之一,尤其是当路径数较少时,前述两种分布模型的实际测量数据非常不准确,常常需要用Nakagami-m分布来进行信道建模[9].其分布如(4)式所示.
(4)
式中Pr—平均功率;Γ(m)—伽马函数;m—衰落参数,m的值越大,衰落越严重,当m=1时得到瑞利衰落.
2 仿真平台设计、测试与分析
2.1 需求分析
GUI是Matlab软件中的图形工具,开发时通过设计所需的代码将字符界面生成图形界面,方便使用者操作选项按钮得到相应的功能,所以它大量应用在信号处理、通信系统分析以及数字图像处理等领域[10].因信号在传输过程中会受到噪声、路径损耗、瑞利衰落、频率选择性衰落等影响,这里主要研究信道衰落对信号传输的影响,为便于学者理解和分析,本文设计一个可视化的移动衰落信道仿真平台,在不同衰落信道模型不同参数下输出相应波形,根据波形结果分析信道传输特性.在设计时离不开无线通信基本原理,其原理框图如图3所示.

图3 无线通信原理框图
2.2 平台设计
该平台主要包括信道类型选择和信道参数设置两个方面,它支持用户手动选择信道模型,然后输入相应的信道特征参数,通过点击确定按钮可实现一键输出信道特性,学者即可直观地观察波形并分析信道衰落特性.具体设计流程如图4所示.
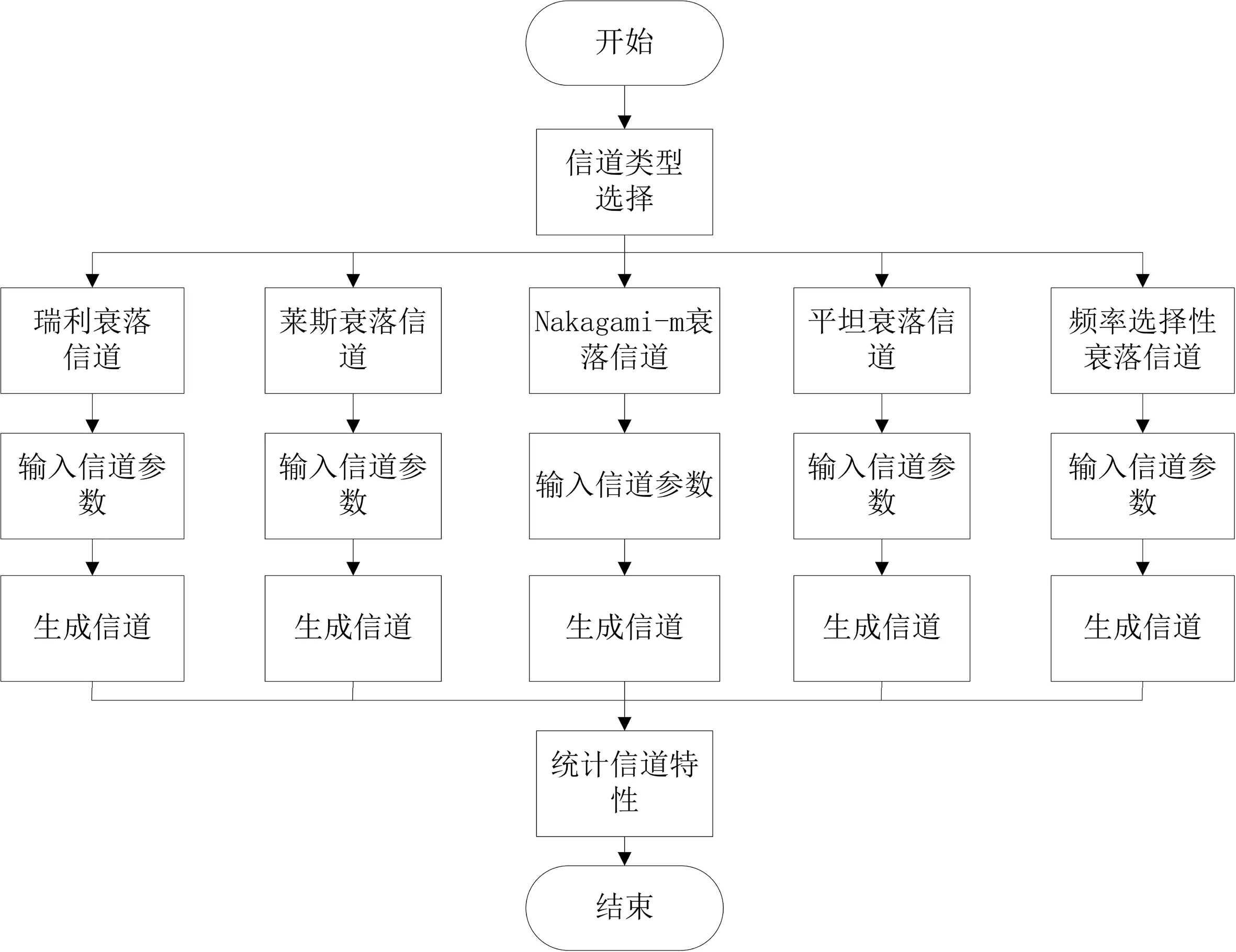
图4 仿真平台设计流程图
首先打开软件建立BLANK GUI文件,完成GUI设计后需要保存.fig和.m文件,缺一不可;然后通过对各控件属性的更改和编写代码来实现功能设计,通过点击菜单栏中的“工具”、“对齐对象”、“属性查看器”等操作美化界面;最后点击“M文件编辑器”编写回调函数等,得到瑞利衰落信道、Nakagami信道、莱斯信道、平衰信道特性和频选信道特性五种可选类型,设计完成后的仿真界面如图5所示.

图5 仿真界面图
以Nakagami-m信道为例,仿真界面如图6所示.界面的最上方设置了平台名称“基于GUI的移动衰落信道的建模与仿真平台”,通过简单静态文本编辑“参数设置”和“信道类型”;然后在Callback函数中编写代码,每一个GUI程序都对应操作它的一个脚本,而在脚本的开头会有相应的函数声明和内置函数,选择完信道之后将会出现一些可以设置的参数;最后点击“确定”按钮将会调用并执行相应函数,利用get()函数和set()函数获取和设置当前的值.同时界面中还包含用来显示采样值和概率密度函数的两个坐标轴,其具体生成坐标和参数的部分代码如下所示.

图6 Nakagami-m信道仿真界面
axes(handles.axes7)
plot(r_,y6);grid on:hold on;
xlabel(‘值的分布’),ylabel(‘概率密度函数(PDF)’);
title(strcat(‘Nakagami信道的概率密度函数理论与实际仿真,m=‘,32,num2str(m),’,Omega=’,32,num2str(omega))).
以上就是仿真平台的整体设计过程.下面将详细阐述平台测试情况.
2.3 平台测试
以瑞利信道为例,若设置数据长度为10 000,步长为0.1,范围为4,仿真结果如图7所示,其概率密度函数的实际值与理论曲线相吻合,这验证了仿真的有效性.
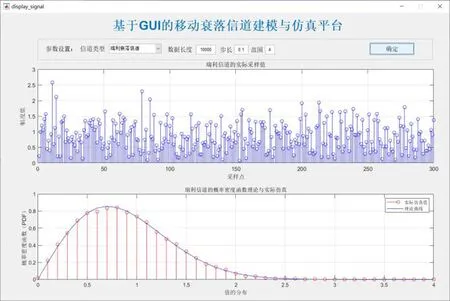
图7 瑞利信道仿真图(步长=0.1)
若修改仿真的数据长度为100 000,采样的步长为0.05,结果如图8所示.结果表明在新的参数配置下,信道的概率密度函数实际值统计特性更加密集,与理论曲线的吻合程度更深,说明增加数据统计量有助于增加信道特性统计的精确程度.

图8 瑞利信道仿真图(步长=0.05)
下面是Nakagami-m信道的仿真情况,其中m为衰落系数,Omiga为信号平均概率.如图9所示数据长度为10 000,步长为0.1,范围为4,m为2.Omiga为0.5.结果表明概率密度函数的实际仿真值与理论值是一致的,并且统计值越多,一致程度越高.

图9 Nakagami-m信道仿真图(m=2)
若将m的值分别改成1和10,其他参数保持不变,仿真结果如图10和11所示.从图中可知,当Nakagami-m信道参数m减小时,统计特性概率密度函数的峰值左移;相反若m值增大时,其峰值则相应地进行右移;特别是当m值增大时,Nakagami-m信道的采样值幅度整体抬升.

图10 Nakagami-m信道仿真图(m=1)

图11 Nakagami-m信道仿真图(m=10)
如图12,13和14所示为莱斯信道的仿真结果.其数据长度设置为10 000,步长为0.1,范围为10,莱斯参数S分别设置为2和4,方差值Sigma也分别设为2和4.图中表明,在不同参数配置下,莱斯信道变量体现出来的统计特性各不相同,当增大莱斯参数S时,莱斯信道概率密度函数统计特性峰值点显著右移;而增加莱斯信道方差值Sigma时,概率密度函数的范围明显增加.

图12 莱斯信道仿真图(S=2)

图13 莱斯信道仿真图(S=4)

图14 莱斯信道仿真图(Sigma=4)
上述三种信道本身具备一定的内在联系,Nakagami-m信道模型是最具有一般意义的模型.当m=1时,Nakagami-m信道退化为瑞利信道,它只有散射分量,没有直射分量;而当m趋于无穷大时,它则转化为莱斯信道,此时不仅有散射分量还有直射分量.通过以上仿真发现,三种信道的概率密度函数实际仿真值与理论曲线完全吻合,这说明了仿真结果的正确性,因此,借助仿真平台可以快速高效地展示不同信道的传输特性.根据上述平台图形化的仿真结果,学者可以直观地观察不同信道参数下各衰落信道的时域波形,抽象的理论知识更加具体形象化,理解起来更容易.
2.4 案例分析
前面主要针对衰落信道本身进行了仿真测试,下面结合具体调制方式在不同信道衰落传输特性下展开分析.如图15、16、17所示分别为QPSK、16QAM和64QAM三种不同调制信号经平坦衰落信道传输后多普勒频移值为0时的仿真情况.通过观察仿真结果可以看出,其星座图未发生明显的发散,只是星座整体发生了一定程度的旋转,整个调制信号的星座图还是非常清晰的;同时它们的发送信号和接收信号功率谱基本保持一致,无明显的频率衰落现象.

图15 QPSK调制经过平坦衰落信道仿真图(fd=0Hz)

图16 64QAM调制经过平坦衰落信道仿真图(fd=0Hz)

图17 16QAM调制经过平坦衰落信道仿真图(fd=0Hz)
若多普勒频移值增加为1 000Hz时,仿真结果如图18、19和20所示.由图可知,QPSK、16QAM和64QAM三种调制信号的星座图发生了非常明显的拖尾现象,尽管频域上其功率谱密度并未发生明显的变化,但信道中的多普勒因素对信号的解调产生了非常不利的影响,需要采用噪声抑制技术才能实现信号的恢复.
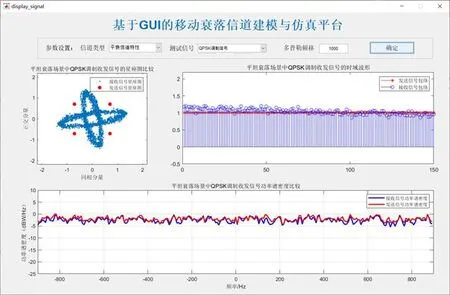
图18 QPSK调制经过平坦衰落信道仿真图(fd=1 000Hz)

图19 16QAM调制经过平坦衰落信道仿真图(fd=1 000Hz)

图20 64QAM调制经过平坦衰落信道仿真图(fd=1 000Hz)
如图21,22,23所示为频率选择性衰落信道中QPSK、16QAM和64QAM三种调制信号的仿真情况.结果表明,它们与平坦衰落信道相比发生了显著的变化,在给定多普勒频移为0Hz的条件下,不同调制信号经过信道传输后,星座图出现了非常明显的发散现象,同时其功率谱密度在不同频点上发生了显著的衰减现象,这也体现了频率选择性衰落的关键特性.
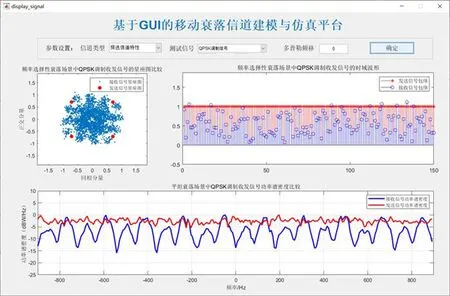
图21 QPSK调制经过频选衰落信道仿真图(fd=0Hz)

图22 16QAM调制经过频选衰落信道仿真图(fd=0Hz)

图23 64QAM调制经过频选衰落信道仿真图(fd=0Hz)
如图24,25,26所示为频率选择性衰落信道多普勒频移值增大为1 000Hz时上述三种调制信号的仿真结果.由图可以看出,不同调制信号的星座图已经完全发散,无法看出信号的调制特征,频域的功率谱密度同样表现出明显的频选衰落特性,此时信道在这类环境下将无法实现正确解调,需要在接收机中引入时、频域均衡技术,对信道的传输特性进行一定程度的补偿,从而恢复出原始信号.上述结果表明,多普勒频移值越大,信道衰落特性越严重,对信号传输影响越大.

图24 QPSK调制经过频选衰落信道仿真图(fd=1 000Hz)

图25 16QAM调制经过频选衰落信道仿真图(fd=1 000Hz)
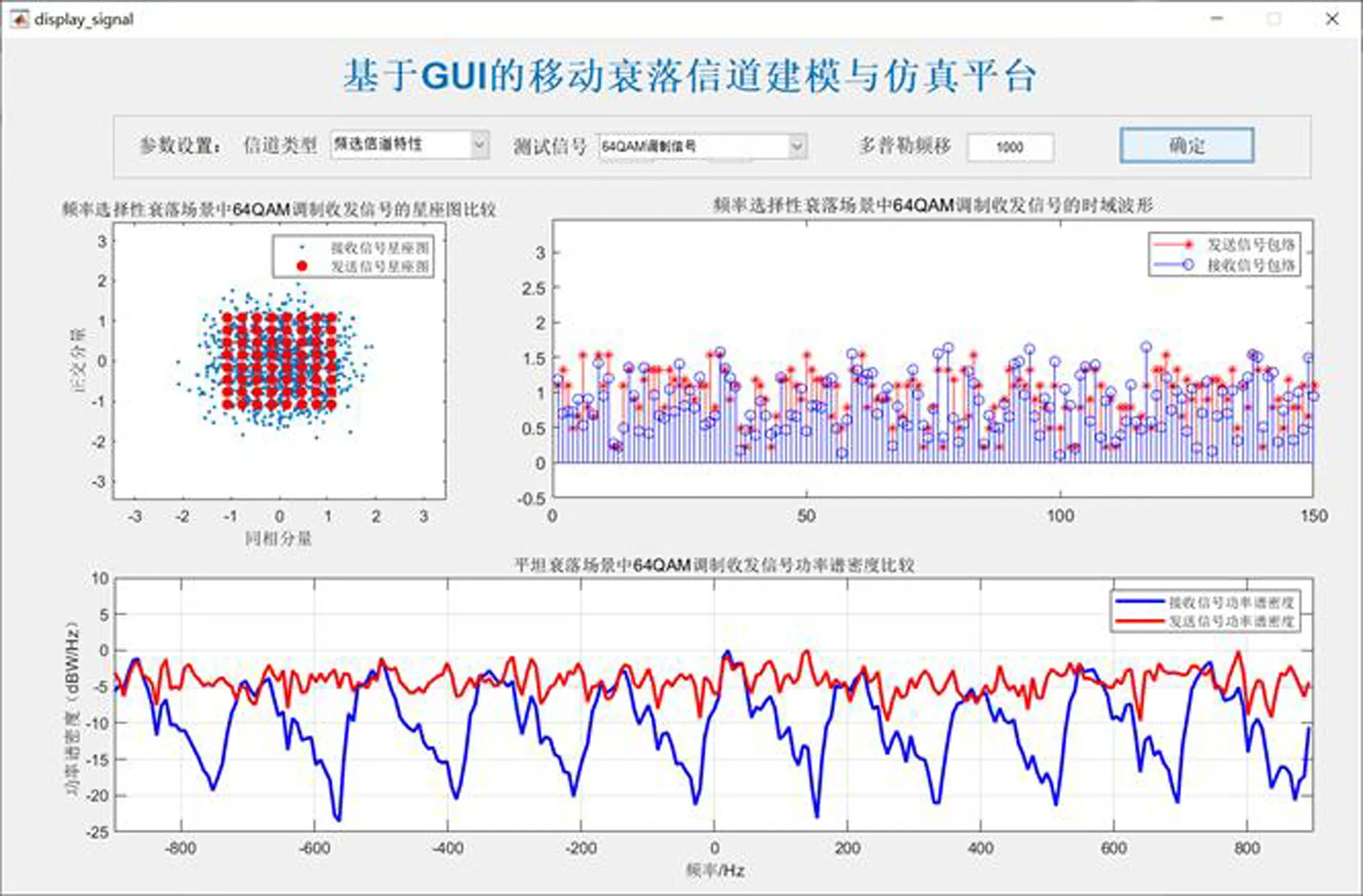
图26 64QAM调制经过频选衰落信道仿真图(fd=1 000Hz)
3 结 语
本文将Matlab GUI应用到移动衰落信道分析中,将枯燥的理论知识生动形象化,学者可调整采样点、数据长度、步长、多普勒频移值等参数得到各信道的衰落分布图形,从而进一步理解信道特性对信号传输的影响.实践表明,该设计平台方便更好地进行实时处理与数据分析,具有较好的应用价值.
