结构参数对气/固两相流偏心异径管冲蚀影响分析

何 鹏，梁裕如，艾昕宇，胡耀强，张成斌，张 铎

(陕西延长石油(集团)有限责任公司 研究院，陕西 西安 710075)

引 言

在气田集输系统中，偏心异径管作为常用的管段连接部件[1]，广泛应用于压缩机的进出口、流量调节阀进出口、温度计扩大管左右以及水套加热炉集合管管端的配管中[2]，可以起到调节气体流速，调整管线走向以及增大管段整体柔性减小管段应力的作用。实际应用中，在大进小出结构中，由于偏心异径管过渡段气体流速迅速增大，天然气中携带的固体颗粒受惯性力作用对过渡段产生不间断的撞击，造成管壁的力学损伤，特别是气田增压稳产阶段[3]，集输系统中压力降低，管输流速增大，力学损伤加剧，从而导致内压作用下的冲蚀穿孔或者破裂，影响管道的安全生产[4]。

目前，针对异径管的冲蚀研究主要集中在同心异径上。吕志鹏[5]等采用数值模拟的手段研究了不同工况下含沙气体对同心异径管的冲蚀磨损影响，得到了最大冲蚀速率随含沙量、结构参数的变化情况以及冲蚀效应发生的主要位置。偶国富[6]等采用数值模拟方法研究了同心异径管的规格及内部流体流向对管壁腐蚀产物保护膜变形的冲蚀影响，得出两端管径差越大或流向为大进小出时冲蚀较为严重。何兴健[7]等采用数值模拟方法研究了同心异径管的冲蚀情况与颗粒入口浓度及异径管结构尺寸的关系，结果发现相同速度下颗粒浓度上升，最大冲蚀速率增大且随变径角度的增大呈现先增大后减小的趋势。

气田现场实际应用中，由于气质组份比较稳定，工况参数相对固定，对偏心异径管冲蚀影响最大的主要是结构参数[8]。为了尽可能减少冲蚀对偏心异径管造成的力学损伤，利用均匀设计结合数值计算的手段，分析了结构变化对其最大冲蚀速率的影响，研究结果可为偏心异径管的结构设计提供一定的理论依据。

1 计算控制方程

1.1 湍流方程

由于偏心异径管过渡段气相流速增长快，速度梯度较高，属于高Reynolds流动，为了更好地描述气相流动特征，采用标准k-ε湍流模型：

(1)

Gk+Gb-ρε-YM+Sk，

(2)

(3)

式中：Gk为平均速度梯度引起的湍动能k的产生项；Gb为浮力引起的湍动能k的产生项；σk和σε分别为与湍动能k和耗散率ε对应的Prandtl数；YM为脉动扩张贡献项；C1ε、C2ε、C3ε为经验常数；Sk和Sε为自定义源项。

1.2 离散相控制方程

在拉氏坐标系下对固体颗粒进行追踪求解，固体颗粒的受力方程为

(4)

(5)

(6)

(7)

式中：up为固体颗粒速度；ρp为固体颗粒密度；dp为固体颗粒粒径；Rep为相对Reynolds数；gy为y方向的重力加速度，取9.81 m/s2；CD为曳力系数；Fy为y方向上其他形式作用力：包括虚拟质量力、压力梯度力、布朗力和Saffman升力；针对球形固体颗粒，Reynolds数取值在一定范围内时，a1、a2、a3为常数，具体取值可参考文献[9]。

1.3 冲蚀模型

1.3.1 冲蚀速率计算方程

采用General冲蚀模型，监测壁面边界上固体颗粒的冲蚀速率：

(8)

式中：Rerosion为壁面的冲蚀速率，kg/(m2·s)；N为固体颗粒撞击数目；mp为固体颗粒质量流量，kg/s；C(dp)为固体颗粒直径的函数；α为固体颗粒对壁面的撞击角，(°)；f(α)为撞击角函数，与撞击角α采用分段线性函数描述，通过激波脉冲试验可测得当撞击角为0°、20°、30°、45°、90°、135°、150°、160°、180°时撞击角函数值分别为0、0.8、1.0、0.5、0.4、0.5、1.0、0.8、0；up为固体颗粒撞击壁面的相对速度，b(v)为此相对速度的函数，取2.6；Aface为壁面计算单元的有效面积。

1.3.2 壁面恢复系数方程

固体颗粒撞击壁面后，运动轨迹发生变化，同时存在动量和能量的损失，在撞击后的反弹过程中动量随着恢复系数发生变化，Forder Rebound Model回弹模型对固体颗粒撞击壁面的速度特性描述较为准确，因此采用模型

10-4α2-2.61×10-6α3，

(9)

10-4α2-3.56×10-6α3

(10)

对恢复系数进行计算。式中，α为固体颗粒的撞击角；V1、V2为撞击前后的速度；eN和eT为法向和切向恢复系数。

2 冲蚀数值计算模型

2.1 管道结构及物性参数

几何模型由3部分构成，分别是进口直管段(管径D1)，偏心异径管段，出口直管段(管径D2)，如图1所示。模型在三维笛卡尔坐标系下建立，坐标原点在上部管壁，重力方向沿Y轴正向，将过渡段入口端面按管径比划分为εD1以及(1-ε)D1，ε为管径比(D2/D1)，过渡段倾角为θ，为避免过渡段内流体产生较大的壁面分离现象，出现大尺度的涡流，θ一般应小于15°[10]。

图1 偏心异径管几何模型Fig.1 Geometric model of eccentric reducer

如图2所示，以入口管径90 mm，管径比0.7，过渡段倾角10°为例，当上、下游直管段长度L1、L2分别取各自管径的10倍时，气相在进入偏心异径管段时流动充分发展，速度边界层汇合于管轴，随轴向距离的增加在径向上的速度分布维持不变。

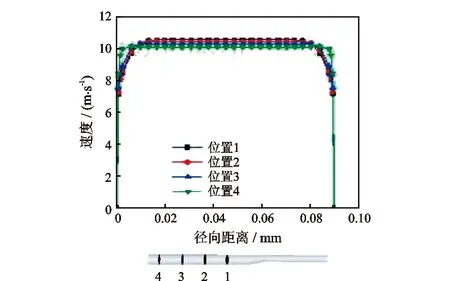
图2 速度径向分布的轴向示意图Fig.2 Axial diagram of radial velocity distribution

离散相固体颗粒的密度为1 550 kg/m3，质量流量为0.000 4 kg/s，依据气田现场实际工况，粒径采用双R分布，见表1。连续相甲烷气体密度为14.523 5 kg/m3，动力黏度为1.12×10-5kg/(m·s)。

表1 粒径分布Tab.1 Particle size distribution

2.2边界条件及数值算法

连续气相：采用标准k-ε湍流模型，近壁面采用标准壁面函数，设置壁面为静止无滑移，速度入口，速度大小为10 m/s，压力出口，出口静压为2 MPa。

离散固相：在DPM模型中进出口使用逃逸(Escape)条件，壁面使用反弹(Reflect)条件，假定固体颗粒为均匀球形，由于连续气相和离散固相间存在较大密度差，除了固体颗粒受到的曳力外，忽略其受到的其他形式作用力[11]。

2.3 网格独立性验证

为了保证计算结果不受网格节点数量影响，对入口管径90 mm、管径比0.7、过渡段倾角10°的偏心异径管最大冲蚀速率进行计算验证，结果如图3所示。由图3可知，当网格节点数量达到304 965时，最大冲蚀速率基本稳定，可以保证计算结果的准确性。

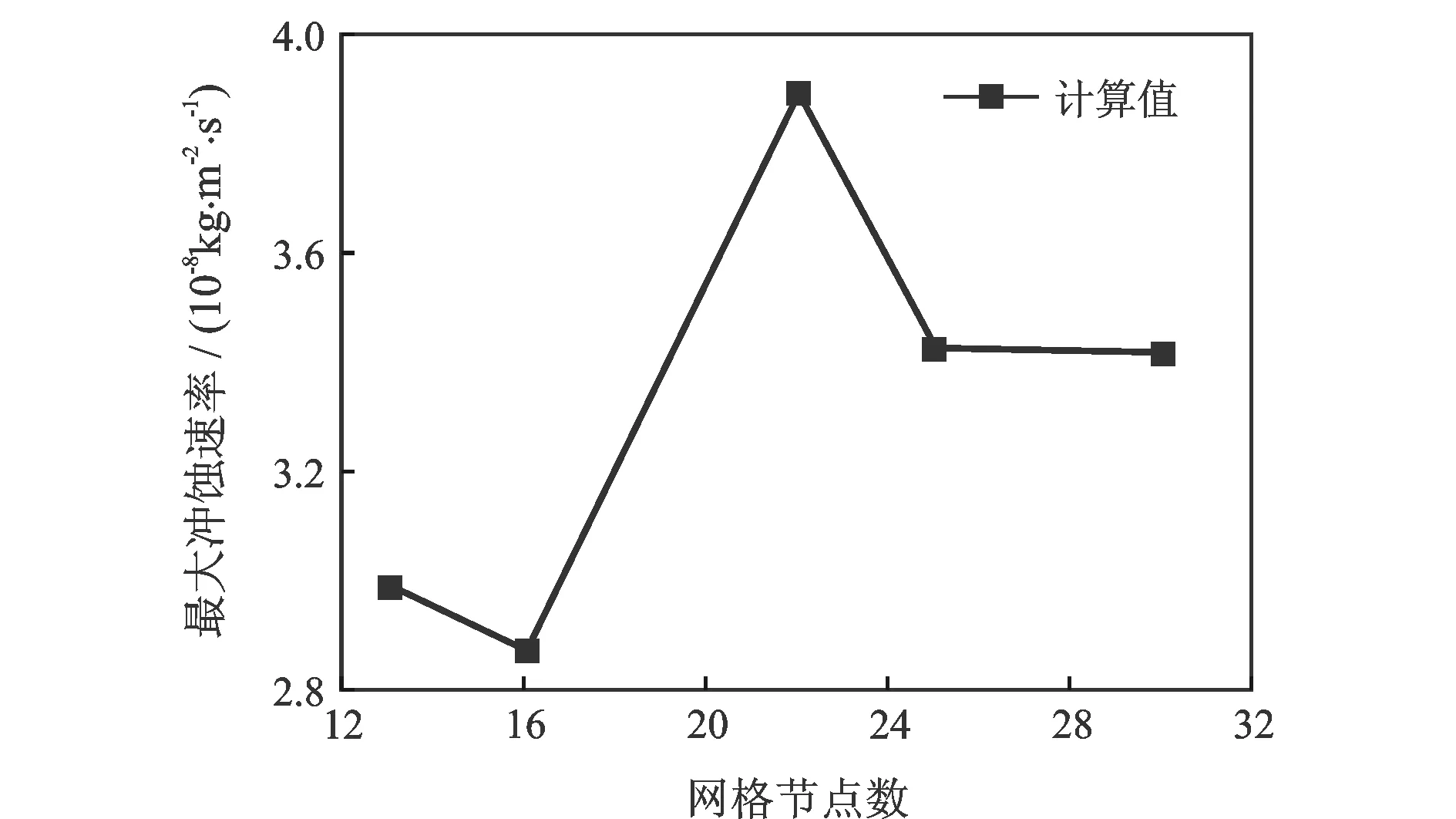
图3 最大冲蚀速率随网格节点变化曲线Fig.3 Variation curve of maximum erosion rate with grid nodes

3 均匀设计方案

最大冲蚀速率作为流动保障的重要安全参数具有重要意义，为了分析结构参数对偏心异径管最大冲蚀速率的影响，采取3因素(入口管径D、管径比ε、过渡段倾角θ)10水平的U10(103)均匀设计表进行数值试验，入口管径50～95 mm，管径比0.35～0.80，过渡段倾角6.0°～10.5°，具体方案设计及计算结果见表2。

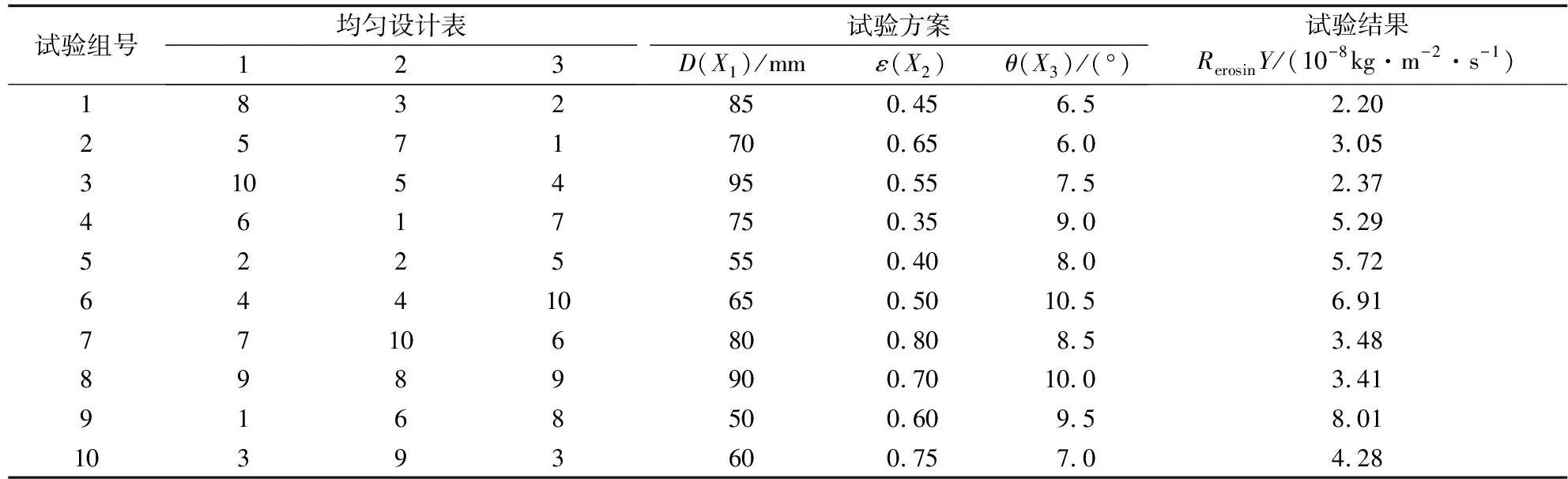
表2 均匀设计试验方案及结果Tab.2 Test scheme and results of uniform design

4 结果分析

首先对入口管径、管径比、过渡段倾角等结构参数进行归一化处理

(11)

采用数据回归分析软件对均匀试验计算结果进行二次多项式逐步回归分析，在α=0.05的显著水平下逐步剔除不显著项后拟合得到经验公式：

Y=3.965 923 43-2.335 475 662 6X1+

5.453 405 809X3-3.290 343 879X1X3-

1.105 600 606 2X2X3。

(12)

式中：Y为最大冲刷速率；X1为入口管径；X2为管径比；X3为过渡段倾角。回归方程的相关系数R=0.994 9，调整后的相关系数Ra=0.990 7，P=0.000 1<0.05，Df(4，5)，F=120.735 1，查询F分布(α=0.05)，F=9.01<120.735 1，表明拟合经验公式回归显著。

将试验结构参数代入经验公式与数值计算结果进行对比，结果如图4所示。由图4可以看出，经验公式计算结果与数值计算结果吻合度较高，趋势基本一致。

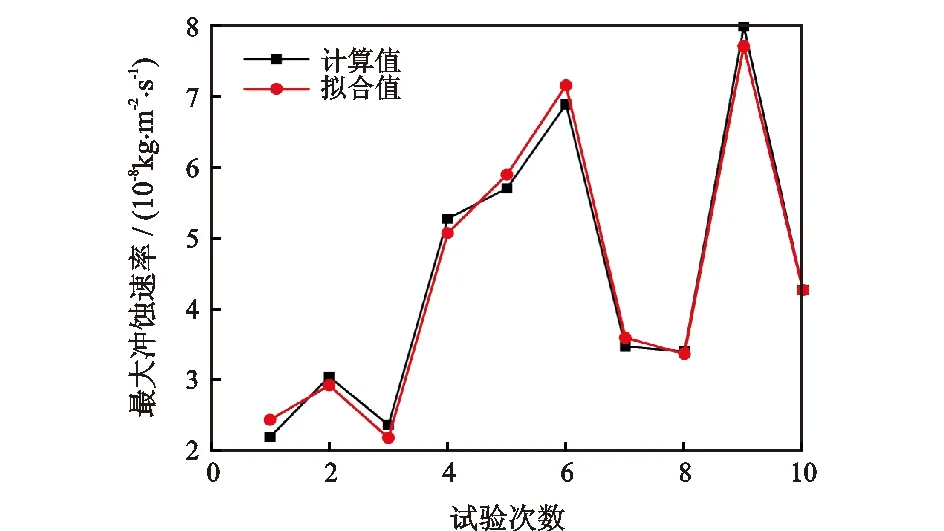
图4 最大冲蚀速率数值计算与经验公式计算对比曲线Fig.4 Comparison of numerical calculation results with empirical formula calculation results of maximum erosion rate

4.1 单因素分析

为单因素定量表征入口管径、管径比以及过渡段倾角对偏心异径管冲蚀速率的影响，取管径比0.7，过渡段倾角10°，入口管径50～90 mm、入口管径90 mm，过渡段倾角10°，管径比0.4～0.8以及入口管径90 mm，管径比0.7，过渡段倾角6°～10°这3种工况进行计算分析。

4.1.1 入口管径和管径比对冲蚀速率的影响

图5、图6分别为不同入口管径和不同管径比的冲蚀示意图。由图5、图6可知，随入口管径或管径比的增大，偏心异径管的冲蚀范围集中在过渡段管壁处且主要分布在D1>y>εD1范围内，最大冲蚀速率出现在变径段入口附近区域。此外，由图6可知随管径比增大，过渡段长度减小，冲蚀影响范围减小。

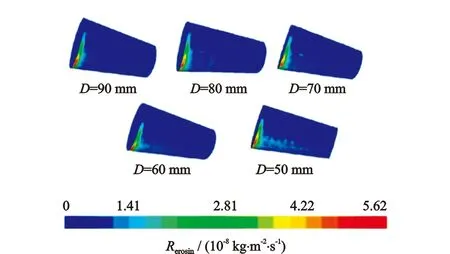
图5 不同入口管径下的冲蚀示意图Fig.5 Erosion diagrams under different inlet pipe diameters

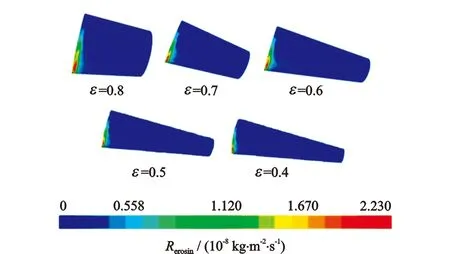
图6 不同管径比下的冲蚀示意图Fig.6 Erosion diagrams under different pipe diameter ratios

图7为不同入口管径下固体颗粒浓度示意图。图7表明，固体颗粒在过渡段入口处的浓度要显著高于其他区域。图8为不同管径比下入口截面速度分布。图8表明，偏心条件下异径管入口端面速度在径向呈现不均匀分布，受过流断面减缩影响，气相向上部端面被挤压，流速高于入口平均流速，管径比越小，入口端面处速度分布的偏心程度越明显。

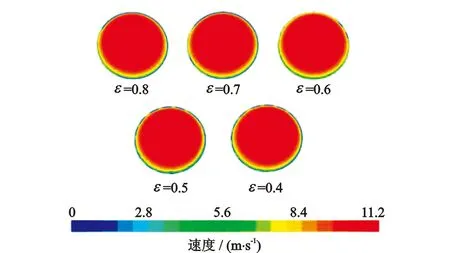
图8 不同管径比下入口截面速度分布图Fig.8 Velocity distribution diagrams of the entrance section under different pipe diameter ratios

图9为入口管径对最大冲蚀速率影响曲线，图10为固体颗粒浓度随管径变化曲线。图9表明，随入口管径增大，偏心异径管的最大冲蚀速率减小，经验公式拟合值与计算值趋势一致。入口管径增大使得过渡段内壁面积变大，单位面积上固体颗粒撞击次数减少，最大冲蚀速率降低。由图10可以看出，随入口管径增大，偏心异径管入口截面D1>y>εD1范围内的固体颗粒浓度随之减小，撞击单位壁面的固体颗粒质量流量减小，最大冲蚀速率相应降低。

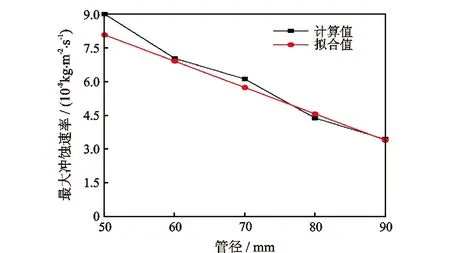
图9 入口管径对最大冲蚀速率影响曲线Fig.9 Influence curve of inlet pipe diameter on maximum erosion rate

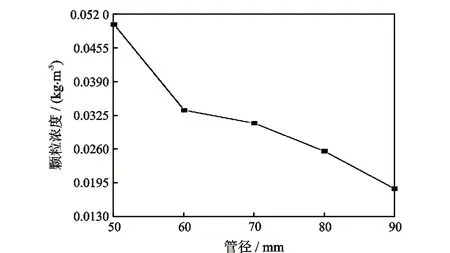
图10 固体颗粒浓度随管径变化曲线Fig.10 Varing curve of solid particle concentration with pipe diameter

图11为管径比对最大冲蚀速率影响曲线。图11表明，随管径比增大，最大冲蚀速率逐渐减小，经验公式拟合值与计算值基本保持一致，管径比的变化会影响过渡段速度场，管径比越小，过渡段的速度变化越剧烈，速度梯度越大。图12为速度随管径比变化曲线。图12表明，管径比越小，过渡段入口端面D1>y>εD1区域气相速度越高，带动固体颗粒以更高的速度撞击过渡段管壁，最大冲蚀速率增大。

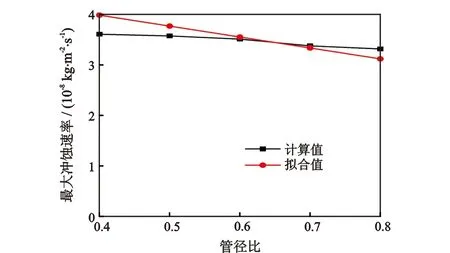
图11 管径比对最大冲蚀速率影响曲线Fig.11 Influence curve of pipe diameter ratio on maximum erosion rate

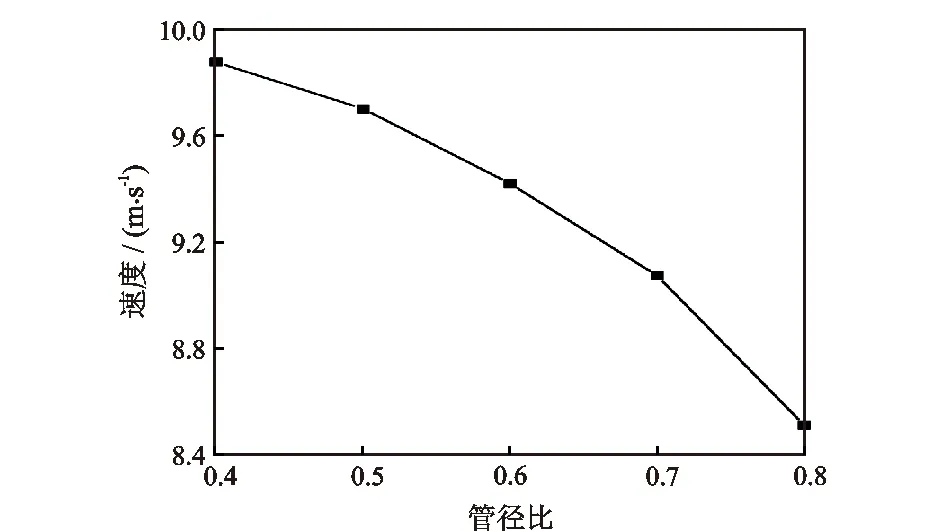
图12 速度随管径比变化曲线Fig.12 Velocity change curve with pipe diameter ratio

4.1.2 过渡段倾角对冲蚀速率的影响

图13为不同过渡段倾角的冲蚀示意图。图13表明，随着过渡段倾角增大，过渡段长度减小，对偏心异径管壁造成的冲蚀影响范围减小，且集中在过渡段处，主要位于D1>y>εD1范围内，最大冲蚀速率出现在变径段入口附近区域。图14为不同过渡段倾角的颗粒迹线示意图。图14表明，过渡段倾角越大，过渡段内固体颗粒运动轨迹的水平夹角越大，运动方向的变化越剧烈，受惯性力影响，对过渡段的壁面撞击越强烈。

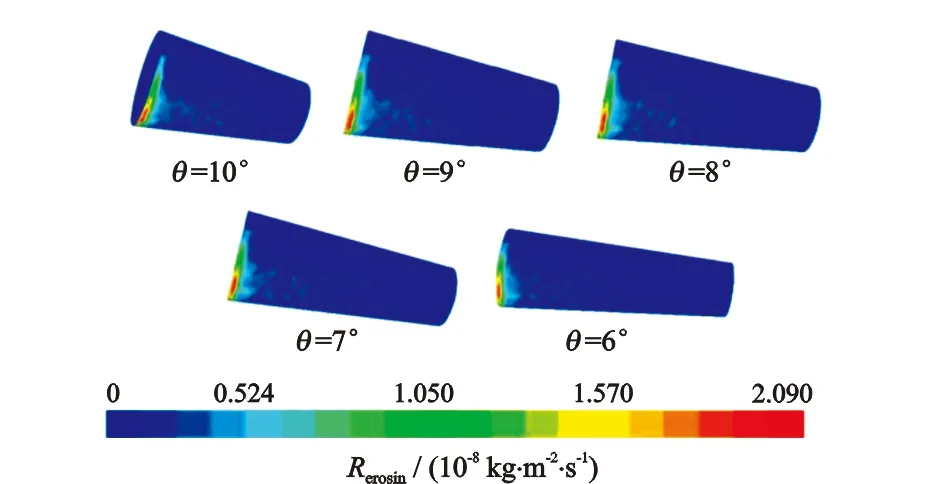
图13 不同过渡段倾角的冲蚀示意图Fig.13 Erosion diagrams under different transition angles

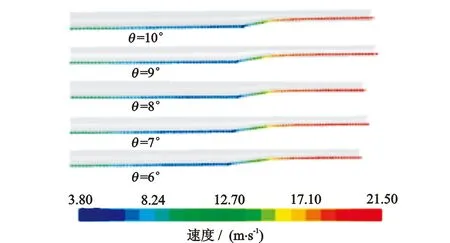
图14 不同过渡段倾角的颗粒迹线示意图Fig.14 Particle trace diagrams under different transition angles

图15为过渡段倾角对最大冲蚀速率影响曲线。图15表明，随着过渡段倾角增大，最大冲蚀速率逐渐增大，经验公式拟合值与计算值的变化趋势基本保持一致。图16为撞击角随过渡段倾角变化示意图。图16表明，当过渡段倾角增大时，固体颗粒与壁面的撞击角也随之增大，过渡段倾角θ与固体颗粒的撞击角α成正比关系。随着过渡段倾角的增大，固体颗粒撞击壁面的方式也由低倾角时的轻微犁削转为高倾角时的正面冲击，倾角越大撞击程度越强烈，最大冲蚀速率相应也越高。

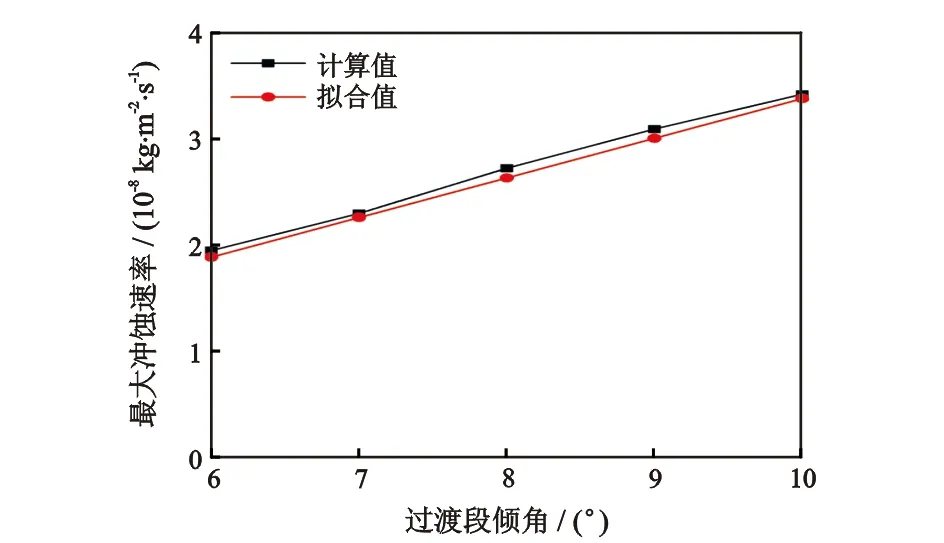
图15 过渡段倾角对最大冲蚀速率影响曲线Fig.15 Influence curve of transition angle on maximum erosion rate

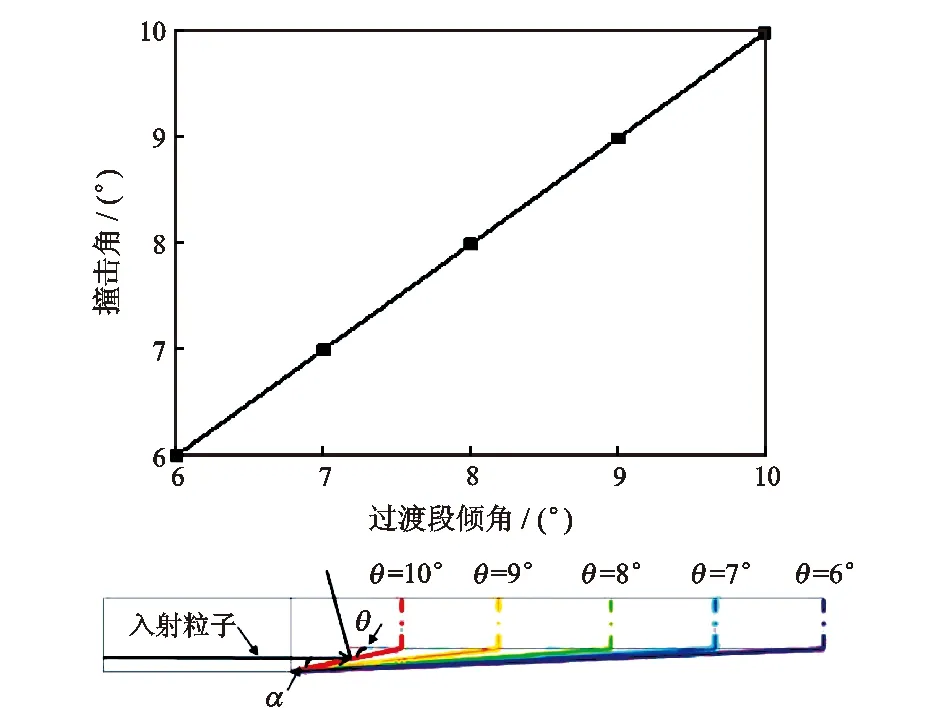
图16 撞击角随过渡段倾角变化示意图Fig.16 Variation of impact angle with transition angle

4.2 各结构参数间交互作用分析

为了进一步分析入口管径、管径比、过渡段倾角3种结构参数的交互作用对偏心异径管最大冲蚀速率的影响，基于拟合的经验公式，绘制了二维等高线云图，图17—图19为入口管径90 mm，管径比0.7，过渡段倾角10°条件下，两因素交互作用的最大冲蚀速率云图，其中入口管径、管径比、过渡段倾角均为归一化后的数值。

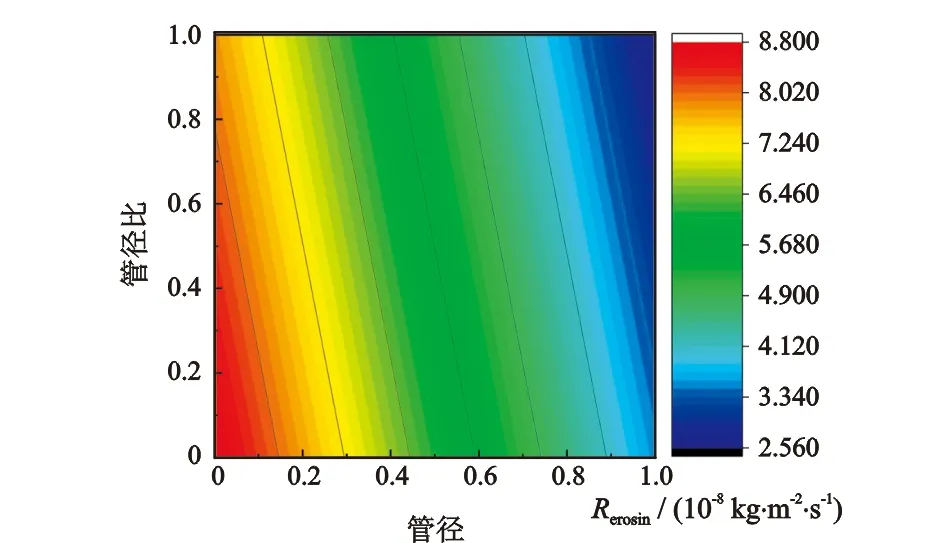
图17 管径、管径比交互作用下的最大冲蚀速率Fig.17 Interaction of pipe diameter with pipe diameter ratio

从图17可以看出，偏心异径管最大冲蚀速率的增加主要是由入口管径所主导，一定入口管径下，管径比的增大对降低最大冲蚀速率的影响较小。从图18可以看出，在入口管径较大时，过渡段倾角增大导致最大冲蚀速率增加，但幅度有限，伴随入口管径减小和过渡段倾角增大，最大冲蚀速率达到最大。从图19可以看出，当管径比增大，最大冲蚀速率随过渡段倾角的增幅要逐渐降低，随管径比的减小以及过渡段倾角的增大，最大冲蚀速率达到最大。

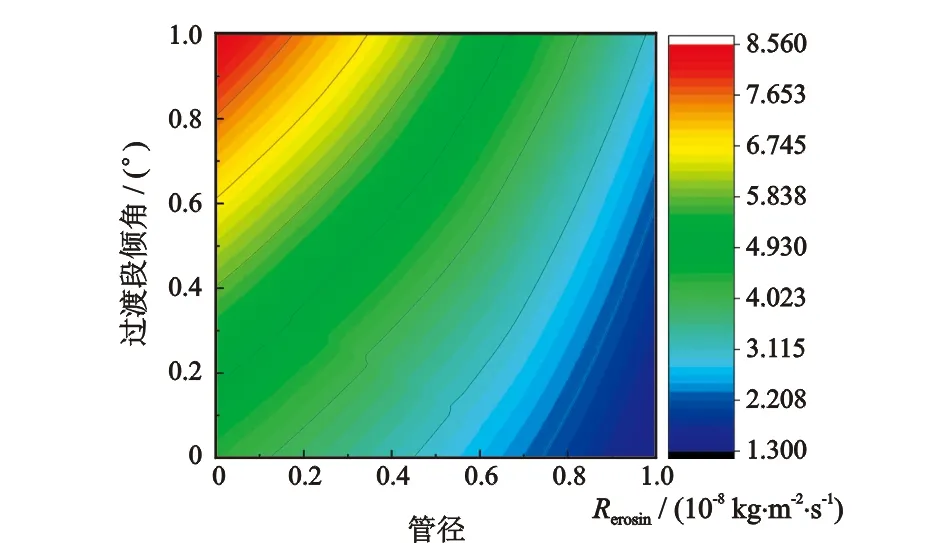
图18 管径、过渡段倾角交互作用下的最大冲蚀速率Fig.18 Interaction of transition angle with pipe diameter

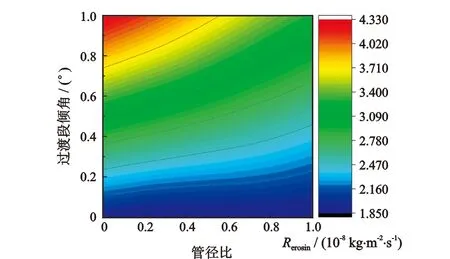
图19 管径比、过渡段倾角交互作用下的最大冲蚀速率Fig.19 Interaction of pipe diameter ratio with transition angle

5 结 论

(1)通过单因素变化的数值计算对拟合经验公式的准确性进行了验证，结果表明经验公式计算结果与数值计算结果误差较小，经验公式较为可靠，可以有效反映结构参数与偏心异径管最大冲蚀速率的关系，进而得到最大冲蚀速率与入口管径呈负相关，与管径比呈负相关，与过渡段倾角呈正相关，且冲蚀区域主要集中在D1>y>εD1范围内，最大冲蚀速率出现在变径段入口附近区域。

(2)基于经验公式，绘制了二维等高线云图，分析了结构参数间交互作用的规律，结果表明入口管径、管径比、过渡段倾角对偏心异径管最大冲蚀速率存在协同作用影响。