基于高斯混合隐马尔可夫模型的螺纹钢价格波动预测

2022-05-31孙若莹

冶金经济与管理 2022年2期

□ 王越孙若莹

一、研究背景

螺纹钢是指钢筋混凝土和预应力钢筋混凝土用钢材，应用于建筑领域，特别是各种大型、重型、轻型薄壁和高层建筑结构[1]。当前，钢铁贸易商通过钢铁B2B电子交易市场进行交易，该类电子市场提供信息服务、线上及远期交易撮合服务，提供公开的螺纹钢市场历史报价、交易量[2]。螺纹钢是22类钢材中唯一完全应用于建筑领域的钢铁材料，市场需求量巨大，且在电子交易市场中可观察到其价格波动较为活跃，因此对其价格波动进行分析和预测具有一定意义。

隐马尔可夫模型（HMM）具有从数据中学习经验知识的能力，其对未来价格趋势的预测主要基于从历史数据中学习到的经验知识，并非完全依赖于人为给定的先验知识，这就使得从数据中挖掘出更多与未来价格相关的信息成为可能[3]。HMM模型通过假设存在不可观测的隐状态序列及其对应的可观测序列，研究隐状态之间、观测状态各自及二者之间的关系。将HMM模型的隐状态理解为一只“看不见的大手”，其意味着相当复杂而不易观测的因素，比如政策变化、螺纹钢需求变化、螺纹钢原材料价格变化等，影响着螺纹钢的最高价、最低价、成交量等可观测状态。

Hassan等[4]首次将HMM模型应用在金融数据上，其将股票的开盘价、收盘价、最高价和最低价作为HMM模型的观测序列，经训练得到HMM模型的参数后，计算当日股票收盘价。Gupta等[5]改进使用股票每日最高价和最低价变化的百分比作为特征训练HMM。张旭东等[6]通过对股票收益率的统计分析，建立了离散型HMM模型，实现对股票价格的预测。余文利等[7]使用 CBIC（Clustering and BIC）算法生成 HMM 模型隐状态的个数，在预测误差大于一定阈值时，模型进行自动更新，建立新模型，得到了较好的预测效果。陈海鹏等[8]提出了一种基于多元线性回归分析的螺纹钢价格分析及预测模型，从影响螺纹钢价格的因素角度建立模型并实现螺纹钢价格预测，该方法不足之处是各因素之间存在多重共线性，可能对预测结果产生干扰。张巧艳[9]引入分形理论，根据螺纹钢价格数据的分型特征，以现货收益率为预测因素，构建了基于粒子群算法的BP神经网络模型，该方法的不足之处在于预测之前必须去噪和获取分形特征，在实际应用中缺乏灵活性。

HMM模型的优势在于其充分挖掘历史数据信息并将其应用于预测，避免了在人为分析价格相关要素的过程中可能产生的遗漏和偏差。高斯混合隐马尔可夫模型（Gaussian mixture hidden Markov model，GMHMM）是在HMM模型基础上，使用高斯混合分布改写观测概率矩阵的改进模型。本文以2维观测序列为输入，使用Baum-Welch算法学习模型参数，再根据Viterbi算法进行市场隐状态解码，构建和训练了GMHMM模型，最后使用加权预测结合移动窗口进行不同时间段的预测。实验结果分析表明，GMHMM模型在螺纹钢现货市场具有适用性，为后续螺纹钢投资策略、库存管理研究等奠定了基础。

二、模型介绍

1.隐马尔可夫模型

HMM模型是基于时间序列的概率模型，其包含一个隐藏的马尔科夫链，由这个马尔科夫链随机生成隐藏的状态随机序列，各个状态根据某种概率函数生成一个观测数据，从而产生一列观测数据[10]。HMM模型状态转移由随机观测与对应的观测随机过程组成。一般可以直接观测到观测状态序列，不能直接观测到隐状态序列，若要得到隐状态序列，可以对观测状态序列进行研究，去推断隐状态序列及其转移特征。

HMM模型的状态定义如下：Q={q1,q2，…qn}，所有可能的隐状态集合；V={v1,v2，…vm}，所有可能的观测状态集合；I={i1,i2，…iT}，隐状态序列；O={o1，o2，…oT}，观测状态序列。定义λ=(A,B,π)为HMM模型，模型由初始概率分布π、状态转移概率分布A及观测概率分布B确定。其中初始状态概率向量πi表示在t=1时处于状态qi的概率，表达式为：

A为状态转移概率矩阵, 描述的是系统在时刻t处于状态qi的条件下，在时刻t+1转移到状态qj的概率，表达式为：B为观测概率矩阵，描述的是时刻t处于状态qj的条件下，生成观测vk的概率，表达式为：

π、A决定状态序列，B决定观测序列。π与A确定了隐藏的马尔科夫链，生成不可观测的状态序列，B确定了如何从状态生成观测，与状态序列综合确定了观测序列。

HMM模型提出了3个基本问题[11]：

（1）概率计算问题。在给定模型参数λ和观测序列V的条件下，计算在该模型λ下出现观测序列O的概率P(O|λ)，通常使用前向-后向算法解决该问题。

（2）学习问题。已知观测序列O，估计模型λ，使得在该模型下观测序列概率P(O|λ)最大。估计模型参数的核心思想是最大似然估计，通常使用Baum-Welch算法实现。

（3）预测问题，也称解码问题。已知模型λ和观测序列O，求对给定观测序列条件概率P（I|O)最大的状态序列I。即给定观测序列，求最有可能对应的状态序列。

2.高斯混合隐马尔可夫模型

原始HMM模型的观测变量为离散随机变量，在螺纹钢行情数据中，观测变量（即价格数据）是连续随机变量，需要利用高斯混合分布来刻画随机变量的分布。高斯混合分布是指多个高斯分布的线性叠加，能拟合非常复杂的密度函数。通过足够多的高斯分布叠加，并调节其均值、协方差矩阵，以及线性组合的系数，可以精确地逼近任意连续概率密度函数[12]。通过高斯混合分布重构观测概率矩阵B的参数，重估公式为：

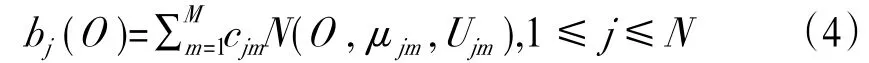
式（4）中，N(O,μjm,Ujm)为多维高斯概率密度函数，M为高斯函数数目，μjm和Ujm分别为均值向量和协方差矩阵，cjm为系数矩阵。通过计算不同维度数组之间的协方差，一定程度上可以反映输入数据的内在关联性，并可在模型进行预测时使用学习到的关联信息。

改进模型被称为高斯混合隐马尔可夫模型（GMHMM），相应的模型参数为：

三、实验与分析

1.数据选取及处理

选取上海大宗钢铁电子交易中心的螺纹钢现货价格数据，基于时效性要求和模型本身特性选取和拆分数据集，以其中2018年4月17日—2021年2月10日的690天数据作为模型的训练数据集，2021年2月10日—2021年3月31日的30天数据作为模型的预测数据集。原始数据维度主要包括high（最高报价）、low（最低报价）、volume（成交量，单位“万吨”）、money（成交额）。

实验数据形式如表1所示。

表1 数据集形式

考虑到市场隐状态会影响螺纹钢最高报价和最低报价，根据隐状态与观测状态之间的生成关系，将high（最高报价）序列和low（最低报价）序列处理后作为观测序列，处理方式为取对数价差值，以更地好体现价格的波动趋势。以high序列数据为例，处理方式见公式（6）。对high序列数据和close序列数据进行处理后，得到2维的观测序列O=(O1,O2)，数据形式如表2所示。

表2 观测序列O=( O1, O2 )

2.模型参数选择

高斯函数数目M的选择：由于观测序列为二维序列O=(O1,O2)，在观测序列中存在2个维度的特征，且2个维度之间存在关联，可使用2个高斯分布的线性组合来描述数据，即M=2。

隐状态数目的选择：GMHMM模型需要定义以对应不同的市场隐状态，使用BIC准则确定该参数值。BIC准则可有效防止模型精度过高造成的模型复杂度过高，其定义见公式（7）。

其中n代表样本大小，k为模型参数数量，L为模型的似然函数。分别计算k在[1,6]范围内对应的BIC数值，数值越小代表该参数下的模型越适合现有数据集，计算结果如表3所示。

表3 不同隐状态数目下的 BIC 值

由表3可知当设定模型的隐状态数目为5时为最优，即所有可能的隐状态集合Q={q1,q2，…q5}，在模型参数λ=(A,μ,U,π)中，μ参数应为5×2的矩阵，U参数则应为5×2×2的张量。

3.实验流程及结果分析

实验共分为2个部分，第一部分是GMHMM模型的建立，第二部分是在GMHMM模型基础上利用价格预测算法进行预测。

（1）GMHMM模型建立

首先，在已知观测序列O=(O1,O2)的情况下，使用Baum-Welch算法得到模型参数λ=(A,μ,U,π)，建立GMHMM模型，然后使用Viterbi算法得到历史隐状态序列S和该序列值对应的隐状态概率矩阵P。实验流程见图1。

图1 GMHMM模型建立及训练流程

A参数为各隐状态之间的转移概率，经过计算其值如表4所示。

表4 A参数矩阵

观察矩阵A发现主对角线上的概率值较高，可推测若市场处于某状态，将倾向于继续保持该状态不变。

模型的参数μ表示观测状态在各个隐状态下的混合高斯概率密度函数均值，其值如表5所示。

表5 参数μ

参数U=[[[0.000 378 08 0.000 241 84],[0.000 241 84 0.000 431 8]],[[0.000 514 19 0.000 437 01],[0.000 437 01 0.000 485 08]],[[0.000 215 94 0.000 149 83],[0.000 149 83 0.000 341 85]],[[0.000 161 19 0.000 119 1],[0.000 119 1 0.000 189 68]],[[0.002 566 17 0.002 492 64],[0.002 492 64]]]。

初始概率π如表6所示。

表6 初始概率π

Viterbi算法可在已知观测序列O=(O1,O2)的条件下，通过计算最有利于观测序列O=(O1,O2)出现的隐状态概率，得到隐状态概率矩阵P=[p1,p2,…pT]，并求出最优隐状态序列S。截取部分隐状态概率矩阵P如表7所示。

表7 隐状态概率矩阵

在表7中，第一天、第二天、第三天市场隐状态概率矩阵中，隐状态4的概率值最大，因此最优隐状态序列S=[4,4,4，…]。实验得到隐状态序列，可对训练数据集的每天市场隐状态值进行观察分析。为便于观察，截取数据集前180天的数据，将每天的观测状态对应的隐状态使用不同标记进行区分，得到的隐状态-观测状态匹配图见图2。

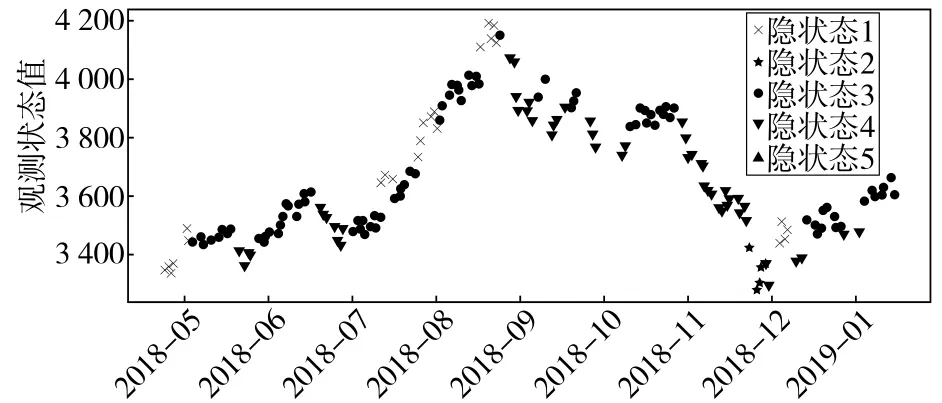
图2 隐状态-观测状态匹配情况

由图2可知，隐状态1对应的标记“×”出现在观测状态值连续上升的区域，推测若市场在隐状态1下，螺纹钢价格上涨可能性大；隐状态3对应的标记“·”出现在观测状态值连续下跌的区域，推测若市场在隐状态3下，螺纹钢价格下跌可能性大；隐状态4对应的“▼”出现在观测值上下震荡的区域，推测若市场在隐状态4下，螺纹钢价格易出现连续上下波动；隐状态2和隐状态5和在图中极少出现，结合隐状态转移概率矩阵P分析原因可知，由其余隐状态转移到隐状态2和隐状态5的概率值极小，因此在实验中所取时段很少出现该隐状态。根据分析结果可知，该数据对应的市场隐状态分为上涨、下跌、震荡和其余2种情况存在，基本符合大众对市场的常识性认知。

（2）价格预测算法

在得到GMHMM模型参数价格后，进行下一步的价格波动预测。预测方法基于2个前提：一是“道氏理论”第三条——历史会重演，因为人类心理具有特殊性且对市场价格波动产生重要影响，当市场参与者心理表现出的规律性反映在价格走势上，市场价格便会出现“重复式”走势，历史便会重演[13]；二是HMM模型的“模式识别”特性，即HMM可以寻找历史上与今天的隐状态最为相似的时刻。

通过GMHMM模型建立得到隐状态概率矩阵P和历史隐状态序列S，在历史序列中取与最后一日的隐状态概率值最接近的单日或多日，将这单日或多日的下一日的观测值的变化作为最后一日的下一日的变化值。对单日匹配预测法和多日加权预测作对比，分别观察其在预测长度为30天时的性能。

——单日匹配预测法的步骤为：

第一，通过隐状态概率矩阵，确定训练集最后一天的隐状态qT，以及这个状态在隐状态概率矩阵中对应的概率值pqT；

第二，选取状态序列概率矩阵P中隐状态为qT的列，在历史概率值中寻找与概率值pqT最相近的1天，记为t0，与该天对应的隐状态概率值记为pt0；

第三，在训练集中取出t0对应的观测状态值Ot0=(Ot01,Ot02)，以及这天的下一天的观测状态值Ot0+1=O(t0+11O,t0+12)；

第四，预测训练集最后一天的下一天的观测值为公式（8）：

第五，将预测值OT+1加入训练集以生成新的训练集，重新输入模型，使用Viterbi算法重新计算新的状态序列概率矩阵，回到算法的第一步开始重复运行算法，直到预测值序列到达测试集长度。

——多日加权预测法的步骤为：

第一，通过隐状态概率矩阵，确定训练集最后一天的隐状态qT，以及该状态在隐状态概率矩阵中对应的概率值pqT；

第二，选取状态序列概率矩阵P中隐状态为qT的列，在历史概率值中寻找与概率值pqT最相近的5天，分别为t1、t2、t3、t4、t5，与这5天对应的隐状态概率值记为pt1、pt2、pt3、pt4、pt5；

第三，令i=5，根据pti与pqT的相近程度计算权重值，使权重值的大小与pti和pqT的相近程度成正比，按公式（9）进行计算：

第四，在训练集中取出t1、t2、t3、t4、t5对应的观测状态值Oti=（Oti1,Oti2），以及这5天的每一天的下一天的观测状态值Oti+1=（Oti+11,Oti+12），i=1，2，…5；

第五，预测训练集最后一天的下一天的观测值

第六，将预测值OT+1加入训练集以生成新的训练集，重新输入模型，使用Viterbi算法重新计算新的状态序列概率矩阵，回到算法的第一步开始重复运行算法，直到预测值序列到达测试集长度。

分别使用单日和多日加权预测法，将二者得到的预测值与测试集进行对比，得到单日匹配预测法预测拟合图和多日加权预测法预测拟合图，分别如图3和图4所示。

图3 单日匹配预测法预拟合

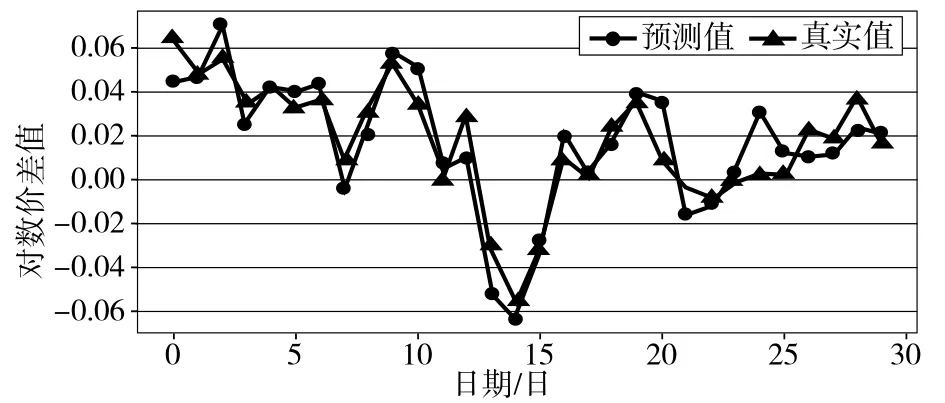
图4 多日加权预测法预拟合

由图3和图4可知：单日匹配预测能在大体上预测行情的走势，但精准度欠缺；多日加权预测在长期的预测中有更好的表现，一般情况下能对观测值的上升和下降有较好的预测，但在预测时段后期的拟合程度下降。

使用常见的预测评估指标平均绝对误差（Mean Absolute Error，MAE）和相对误差绝对值平均（Mean Absolute Percentage Error，MAPE）来评估2种预测方法，2种指标的定义如公式（11）和公式（12）。

分别计算单日匹配预测法和多日加权预测法的MAE、MAPE值，结果如表8所示。

表8 模型预测精度对比

由表8可知，多日加权预测的MAE值和MAPE值均小于单日匹配预测，说明在预测长度为30天时，多日加权预测的性能优于单日匹配预测。多日加权预测法预测天数比单日匹配预测法要长，MAPE值小于1意味着模型具有可行性。

四、结束语

1.研究结论与不足

本文通过GMHMM模型对螺纹钢行情的走向进行预测，证明该模型可通过混合高斯概率密度函数较好地刻画市场行情序列，并且可结合市场的“历史重演”模式和隐马尔可夫的“模式识别”特性进行短期预测。同时，研究具有一些不足：在指标选取上，模型输入只包含螺纹钢的行情数据，但螺纹钢的行情与螺纹钢上游产品如铁矿石和热卷存在一定的关联关系，未来可考虑将其加入模型输入指标；在模型可行性上，隐马尔可夫模型假设每一天的状态仅与前一天的状态相关，在实际状况中可能还受其他时刻状态的影响，因此可将观测状态与自回归模型结合，认为隐状态会产生一系列相互转化的观测状态。