考虑多工序设备权重的资源协同综合调度算法

周 伟 谢志强

(哈尔滨理工大学计算机科学与技术学院 哈尔滨 150080)

1 引言

调度问题作为制造系统的关键环节，一直受到学术界的广泛关注。高效的调度系统既可以降低产品制造的各项成本，又可以提高企业的经济效益、社会效益等。随着计算机技术的发展和社会需求的变化，制造行业的产品调度也随之改变[1–15]。例如，王卓昊等人[1]构建了一套分布式抽取、转换再加载的任务调度框架，优化了复杂任务的调度执行时间；胡致远等人[2]提出了非工作保持型的多节点联合调度模型，保障了业务确定的可达性需求；王萍等人[3]针对动态负载环境下的高效分布式资源分配问题，提出了一种预留—重用联合的Q学习型半持续调度算法等。但是产品制造的多样化和人们需求的个性化，使得小批量、复杂工艺的产品调度问题日益突出。不同于传统工业中的流水调度(flow-shop)和车间调度(job-shop)问题，谢志强[16]提出了第3类产品制造调度模式，即在具有树形复杂结构的多品种、小批量产品中，将产品加工和装配进行同步处理的综合调度，并针对综合调度开展了深入研究，已取得了较丰富的成果[17–26]。

例如，文献[17]针对柔性集成调度问题，提出了基于网络设备协作的改进人工蜂群算法；为解决综合调度智能优化算法中，编码方式遗漏最优解的问题，文献[18]提出了动态优先级约束表的编码方法，保证了初始种群个体的可行性和完备性；文献[19]为解决资源服务器状态动态变化对工作流的调度问题，基于时间窗曲线模型和平均利用率模型提出了考虑资源状态动态反馈的算法等。

但是，在以“工序”为优化对象的研究中，如果算法以长路径为研究主线，那么当相同设备出现短路径上叶节点工序较早开始加工的情况时，首次适用调度策略就会失效，会在工序之间产生不可利用的空闲时间；在以后续工序排序为主线的算法中，加工工序较多的设备上会形成工序序列间的众多加工空隙；在以设备驱动并行为主线的算法中，当后续工序路径长度相同时，如果两个工序都是叶节点工序，那么短用时策略就会失效，纵向优化调度效果不佳，加工工序较多的设备上也会出现很多空闲时间段。

近年来综合调度中以“设备”为优化对象的相关研究较少，只有文献[24]的关键设备工序紧凑调度算法和文献[25]的关键设备工序紧凑的动态调度算法。二者的相同之处是：均将加工用时最长的设备定义为关键设备，然后在关键设备上应用拟关键路径方法，最后应用最佳适应方法在设备空闲时间段插入独立工序。不同之处在于：在文献[24]的算法中关键设备和关键路径是固定的，而文献[25]的算法中关键设备和关键路径是根据部分工序加工完成情况动态调整的。但是，当关键设备上加工工序的前序工序不是独立工序时，两种算法都会在关键设备上产生很多无法利用的空闲时间段，进而拉长了串行工序之间的空隙。

针对目前多品种、小批量复杂产品综合调度中，加工工序较多的设备在调度时出现较多空闲段的问题，本文提出了考虑多工序设备权重的资源协同算法。本文的主要贡献有：

(1)在综合调度领域中拓展了特殊设备的定义范畴：在柔性设备、批处理设备、关键设备、加工中心之外，定义了多工序设备；

(2)算法全面考虑了综合调度领域中的相关因素，如复杂产品工艺树结构、工序自身属性、工序之间的约束关系、设备加工情况等，在此基础上，提出了权重值策略和最佳调度时刻策略；

(3)算法以“多工序设备”作为优化对象，优先调度多工序设备上竞争相对紧张的工序，既提高了多工序设备上工序连续加工的力度，又联动其紧后工序及后续工序的尽早开始加工，有效地减少了产品的加工时间，进而优化了综合调度的整体效果。

2 问题及建模

假设综合调度系统中有m台加工设备，共需加工完成复杂产品的n道工序，每个工序自身加工用时已知，记为di，具体要求如下：

(1)每个工序具有工序序号、对应加工设备序号和自身加工用时的属性；

(2)设备加工工序时，具有时间确定性和加工连续性；

(3)除了叶节点工序，其他任何一道工序可以被加工的充分必要条件是其所有紧前工序均加工完毕；

(4)所有设备上最后一道工序加工完成的时间为产品的总加工用时。

综合调度的优化目标为合理调度各个设备上的工序，最小化复杂产品最大加工用时；约束条件为除了叶节点工序具有紧后工序、根节点工序具有紧前工序以外，其他所有节点工序均存在紧前紧后工序约束关系。

建立问题模型如下：

优化目标

3 算法设计思想

3.1 相关定义

定义1 工序优先级。根据“减少并行工序加工时间”的原则，文献[26]针对复杂产品工艺树中的加工工序提出了工序优先级问题，即将工序调度的优先顺序定义为工序的优先级[26,27]。假设产品加工工艺树有n层，则将根节点工序的优先级定义为1；根节点工序的所有后裔节点工序的优先级定义为2，同层工序节点作为兄弟节点；以此类推，直到第n层的所有节点的优先级定义为n。定义根节点工序的优先级最低，第n层上工序的优先级最高。

定义2 设备优先级。假设综合调度系统有m台加工设备序列{M1,M2,...,Mm}，定义加工工序数量最多的设备优先级最高，加工工序数量次多的设备优先级次之，以此类推，加工工序数量最少的设备优先级最低为1，允许存在相同的设备优先级。

定义3 约束度。以某一工序为中心，将与其直接相邻的所有具有紧前紧后约束关系的工序数量之和，定义为此工序的约束度。

定义4 权重值。将工序的层优先级、设备优先级和工序约束度的数值之和定义为此工序的权重值。

定义5 最佳调度时刻。对于某一工序而言，将其紧前工序(组)加工结束的时刻定义为此工序的最佳调度时刻。

3.2 算法描述

现有综合调度算法的调度过程多以复杂产品工艺树中工序的路径、是否为叶节点工序以及工序的加工用时等因素为考量，较少考虑调度过程中设备的制约条件。与其他综合调度算法不同，本文充分考虑了多工序设备的优化对综合调度总体优化效果的重要作用，设计了层优先级和权重值的排序策略以及最佳调度时刻的调整策略。

层优先级策略是综合调度中的经典策略，主要作用是通过缩短并行工序加工时间的方式优化调度效果。优势主要体现在：(1)约束力强的紧前工序具有优先调度的先决条件；(2)以“层”为单位，优先调度的加工工序可以在不同的设备上同时加工。

权重值策略是算法的核心策略，通过提高多工序设备的利用率带动综合调度设备总体利用率的提高。优势主要体现在：(1)遵循了综合调度中“设备忙”的原则；(2)首次将工序的紧前紧后约束度作为考量因素，提高了多工序设备上工序的衔接度，促进综合调度效果的总体优化。

最佳调度时刻调整策略，有效地提高了设备并行处理的力度。优势主要体现在：(1)对于约束度不强的叶节点工序，具有在对应设备上最早开始加工的优势；(2)对于约束度较强的非叶节点工序，减少了其在设备间的串行空隙。

算法具体描述如下：

步骤1 根据复杂产品工艺树的结构特征，确定工艺树的层序，计算各个工序的层优先级；

步骤2 根据复杂产品工艺树的属性特征，计算各个工序的设备优先级、约束度和权重值；

步骤3 确定层优先级最高的工序；

步骤4 判断层优先级最高的工序是否唯一，如果是，则直接调度，如果否，则转步骤5；

步骤5 判断工序的权重值是否相同，如果是，则转步骤6，如果否，则按照权重值由大到小依次调度工序；

步骤6 根据最佳调度时刻调整策略，调整工序在对应设备上的最佳调度时刻；直到根节点工序调度结束，算法框架流程图如图1所示。

图1 算法框架流程图

3.3 数据标准化处理

复杂产品工艺树结构可以通过虚拟根节点的方式构造更加复杂的复杂产品，因此产品的加工规模和复杂程度不尽统一；同时，由于制造系统中相关设备的情况也不尽相同，所以在采用本文算法进行权重值计算前，需要将工序的层优先级、设备优先级和工序约束度的具体数值进行标准化处理，目的是使不同量纲级别的数据经过计算后得到的结果不会出现偏差。

本文选取在数据处理中常用的Z-score标准化方法[28]，如式(4)所示

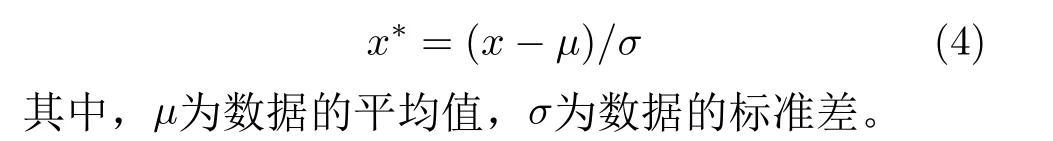
3.4 算法复杂度分析

假设复杂产品的加工工序数、加工设备数和每道工序的自身加工用时等信息均已知，分别设为n,m,di，则本文算法复杂度分析如下：

4 实例分析

本文算法具有普适性，对其他算例亦有较好的调度效果。为便于读者理解本文算法，现举例说明，如图2所示，假设复杂产品A加工工艺树由12道工序组成，分别在4台设备上进行加工。

图2 复杂产品A加工工艺树

根据本文算法，首先计算各设备优先级，如表2所示。其次分别计算各个工序对应的层优先级、约束度、权重值和最佳调度时刻，如表3所示。

表1 考虑多工序设备权重的资源协同综合调度算法

表2 复杂产品A设备优先级统计

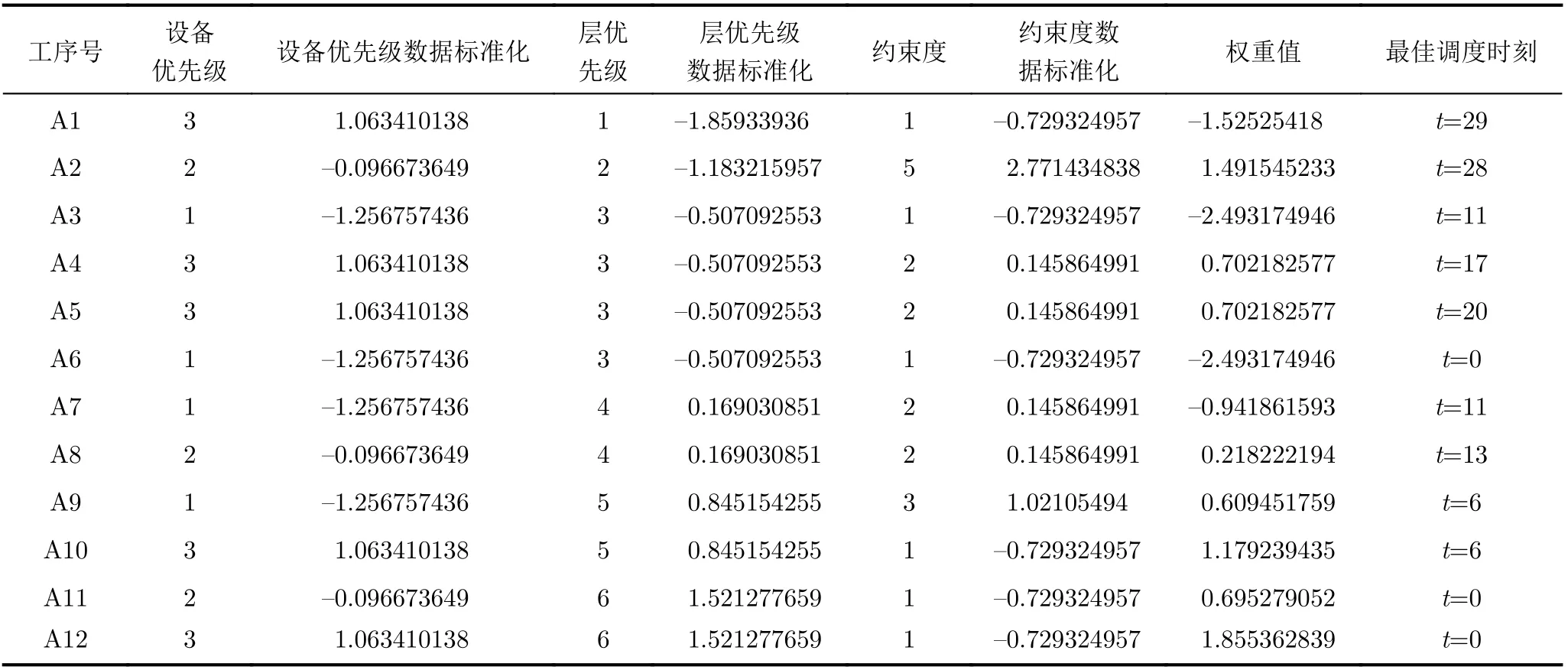
表3 复杂产品A工序权重值统计

调度过程如表4所示，调度甘特图如图3所示，总加工用时为30工时。

图3 复杂产品A加工甘特图30工时

表4 复杂产品A调度过程

5 算法对比分析

5.1 以工序为研究对象的算法对比分析

为阐述本文算法的更优性，现选择文献[20]中的复杂产品B作为实例进行分析阐述，如图4所示。再选择文献[20]紧密衔接工序组联动的算法、文献[21]考虑串行工序紧密度的择时算法与本文算法进行对比分析。

图4 复杂产品B加工工艺树

针对复杂产品B加工工艺图，采用本文算法工序调度顺序为{A3, A2, A1, A4, A10, A5, A11, A12,A6, A18, A7, A8, A13, A20, A19, A21, A9, A10,A15, A22, A24, A23, A7, A25, A17, A26, A27}，调度甘特图如图5所示，总加工用时为27工时。

采用文献[20]紧密衔接工序组联动的算法，工序的调度顺序为{A10, A12, A1, A2, A3, A4, A5, A7,A6, A8, A9, A11, A13, A14, A15, A18, A19, A20, A21,A22, A23, A24, A25, A16, A17, A26, A27}，调度甘特图如图6所示，总加工用时为28工时。

采用文献[21]考虑串行工序紧密度的择时算法，初始调度方案为{A27, A26, A17, A16, A15,A9, A8, A6, A4, A3, A1}，在此基础上按照{A25,A23, A21, A20, A18, A14, A13, A11, A10, A24,A22, A7, A2, A12, A19, A5}的顺序进行调整。因算法采用逆序调度，在保证各工序约束条件的前提下，逆序调整调度甘特图如图7所示，总加工用时为31工时。

5.2 算法结果对比分析

针对复杂产品B加工工艺图，本文算法的总加工用时最少，之所以本文算法更优，主要是因为：

文献[20]的算法优先调度“紧密衔接工序(组)中的工序”，忽略了约束度不高的工序(组)的相对位置对调度结果的影响，因而在工序串行调度过程中产生了空闲时间段。例如在图6中，设备M2在t=17～t=24时刻出现较长时间的空闲，设备M2在整个加工过程中共计有10个工时的空闲，多于图5中设备M2的7个工时的空闲。

文献[21]算法在用择时调度策略确定工序加工开始时间点时，没有充分考虑到多工序设备的加工和利用情况，因而影响了整体调度效果。例如在图7中，设备M2在t=0～t=2, t=5～t=7和t=14～t=18,t=19～t=24时刻一直处于空闲状态；而在图5中，工序A2, A3, A8, A24, A25比图7中的开始加工时间分别提前了7个工时、8个工时、8个工时、10个工时和6个工时，不仅提高了多工序设备M2上工序连续加工的紧密度，而且设备利用率也提高了14.6%。

图5 本文算法调度复杂产品B工艺树甘特图27工时

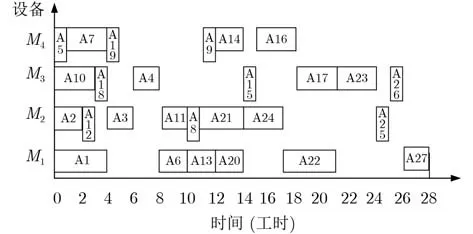
图6 文献[20]算法调度复杂产品B甘特图28工时

图7 文献[21]算法调度复杂产品B逆序甘特图31工时

5.3 以设备为研究对象的算法对比分析

下面再将本文算法分别与同类代表性论文—文献[24]和文献[25]的算法进行对比分析，结果同样证明了本文算法的更优性。

(1)与文献[24]关键设备工序紧凑的算法对比。在文献[24]中，将加工工序用时最长的设备定义为关键设备，在本文中，将加工工序数量最多的设备定义为多工序设备。那么，本文有必要针对多工序设备上工序(组)总加工用时(下述简称前者)与关键设备上工序(组)总加工用时(下述简称后者)的3种不同情况进行详细对比分析。

(2)前者小于后者的对比分析。在复杂产品B加工工艺树中，本文算法中的多工序设备为M2，设备M2对应加工的8个工序(组)为{A2, A3, A8, A11,A12, A21, A24, A25}，总用时15工时；文献[24]算法中关键设备为设备M1，对应加工的6个工序(组)为{A1, A6, A13, A20, A22, A27}，总用时16工时。

采用文献[24]的算法，工序调度顺序为{A1,A2, A3, A4, A5, A6, A7, A8, A9, A10, A11, A12,A13, A14, A15, A16, A17, A18, A20, A19, A21,A22, A23, A24, A25, A26, A27}，调度甘特如图8所示，总加工用时41工时。

图8 文献[24]算法调度复杂产品B甘特图41工时

当多工序设备上工序(组)总加工用时小于关键设备上工序(组)总加工用时，本文算法更优。

对比分析甘特图图5和图8：在图5中，设备M4上的总加工用时为18工时、设备M3上的总加工用时为25工时、多工序设备M2上的总加工用时为22工时、设备M1上的总加工用时为27工时；在图8中，设备M4上的总加工用时为21工时、设备M3上的总加工用时为39工时、设备M2上的总加工用时为38工时、关键设备M1上的总加工用时为41工时。在图8中设备M2上在加工过程中出现了共计23个工时的空闲，明显多于图5中的7个工时的空闲时间段。设备利用率对比分析如表5所示，本文算法设备总体利用率相对提高率提高了20.6%。

表5 前者小于后者时两种算法的设备利用率对比分析

(3)前者大于等于后者的对比分析。由关键设备的判定条件可知，当前者大于等于后者时，对于同一复杂产品工艺树而言，多工序设备和关键设备为同一个设备。下面，本文以图9所示的复杂产品C工艺树为例进行对比分析。

图9 复杂产品C加工工艺树

在复杂产品C加工工艺图中，因设备M3加工工序数量最多：6个，所以多工序设备为M3，又因设备M3上加工工序(组)的加工用时最长：160工时，所以在本例中，设备M3既是多工序设备又是关键设备。

采用本文算法工序调度顺序为{A19, A18,A17, A11, A13, A14, A12, A15, A16, A8, A5, A6,A9, A10, A7, A3, A4, A2, A1}，调度甘特图如图10所示，总加工用时为200工时。

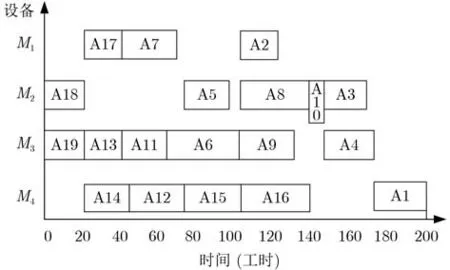
图10 本文算法调度复杂产品C甘特图200工时

采用文献[24]的算法工序调度顺序为{A19,A17, A11, A12, A5, A6, A2, A18, A14, A15, A8,A13, A7, A9, A3, A16, A10, A4, A1}，调度甘特图如图11所示，总用时240工时。

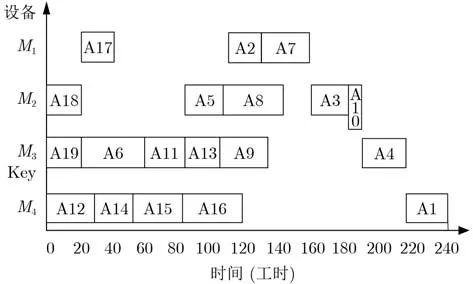
图11 文献[24]算法调度复杂产品C甘特图240工时

当多工序设备上工序(组)总加工用时大于等于关键设备上工序(组)总加工用时，本文算法更优。

对比分析调度甘特图图10和图11：在图10中，多工序设备M3的总加工用时为175工时，工序A13作为叶节点工序使用本文算法的最佳调度时刻调整策略，在t=20时刻开始加工，因此其紧后工序A7较图11中的开始加工时刻提前了90个工时；同时设备M3也仅仅在t=135时刻到t=150时刻之间出现了15个工时的空闲时间段。在图11中，关键设备M3的总加工用时为215工时，设备M3在t=135时刻到t=190时刻的55个工时内，一直处在空闲状态。而在设备利用率方面，文献[24]设备总体利用率为59.6%，本文算法设备总体利用率为72.4%，相对提高了12.8%。

(4)与文献[25]关键设备工序紧凑的动态调度算法对比。文献[25]算法的主要特点是“动态”，即在“拟关键路径+最佳适应调度时刻”的基础上，将最先确定的关键产品部分加工后，再根据设备上对应工序总加工用时的长短动态调整关键产品和关键设备。下面，本文以文献[25]中的复杂产品A和B实例为例，如图12所示，与本文算法进行对比分析。结果同样表明，本文算法更优。

图12 文献[25]原文实例复杂产品A和B加工工艺树

采用本文算法，工序调度顺序为{A1, A4, A3,B1, A2, A5, B2, B3, A6, A7, B4, B5, A9, A8,A10, B6, B7, B8, A11}，调度甘特图如图13所示，总加工用时为235工时。

由文献[25]原文可知，在t=55时刻动态调整关键设备，在t=130时刻动态调整关键产品，在t=55时刻调度效果达到最佳，调度甘特图如图14所示，总加工用时为255工时。

对比分析调度甘特图13和图14：在图13中，多工序设备M2上的总加工用时为235工时，在t=0时刻，设备M1、设备M2和设备M3均开始加工工序；在图14中关键设备M2上的总加工用时为255工时，设备M1从t=0时刻t=20时刻处在空闲状态。本文算法中叶节点工序B2在图13中在t=0时刻开始加工，那么与工序B2具有紧后约束关系的工序(组)也较早开始加工，例如工序B3在图13中较在图14中提前了100个工时，所以本文算法通过优先调度多工序设备上的叶节点工序，联动了其具有较高紧后约束关系的工序(组)也实现了较早开始加工，进而减少了复杂产品的总加工用时。设备利用率对比分析如表6所示，本文算法较文献[25]算法的设备总体利用率相对提高了10.3%。

表6 本文算法和文献[25]算法设备利用率对比分析

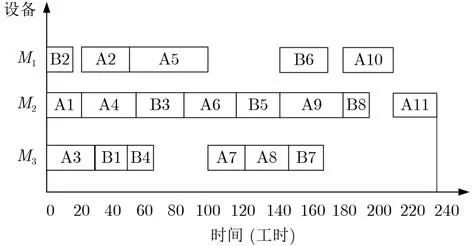
图13 本文算法加工文献[25]原文实例甘特图235工时

图14 文献[25]在t=55时刻加工甘特图255工时

5.4 本文算法、文献[24]算法和文献[25]算法结果对比分析

通过与文献[24]和文献[25]的算法对比分析，之所以本文算法更优，主要是因为：

(1)本文算法采用了“层优先策略”纵横优化的思想，而文献[24]和文献[25]的算法均采用的“拟关键路径”策略是纵向优化的思想，从而拉长了串行工序的加工空隙。例如在图11中，设备M1在t=0～t=20时刻、t=40～t=110时刻，设备M2在t=20～t=85时刻，设备M3在t=135～t=190时刻，设备M4在t=120～t=215时刻均出现了连续且大段的空闲时间；在图14中，工序B2在t=100时刻才开始加工，比在图13的开始加工时刻延迟了100个工时。

(2)本文算法采用了“权重值策略”，在优先考虑多工序设备加工情况的基础上，又全面考虑了加工工序间的各种约束关系。而文献[25]的算法中只考虑了“仅具有唯一紧前、紧后关系的相关工序和独立工序”，也就是仅考虑了约束度小于等于2的节点工序情况，这必然会影响约束性强的工序，导致工序间的紧密衔接性较弱。例如在图13中，因工序B2的优先调度，既利用了设备的空隙又使其紧后工序B3较早开始调度，从而联动了工序B3的后续工序(组)也得到了较早的调度，有效地减少了设备上的加工空隙，缩短了综合调度总体加工用时。

(3)本文算法采用了“最佳调度时刻调整策略”，首先保证了工序(组)紧前关系的约束条件，而在设备空闲时间段查找并插入相关工序则是完全利用设备的调度空隙，充分弥补了文献[24]和文献[25]的算法因加工工序拉伸或者后移而产生的串行工序间的空隙。文献[24]算法采用的“最佳适应调度”策略，当层优先级较低的叶节点工序不是“独立工序”时，“工序紧凑”的策略则会失效。例如图11中设备M3上的叶节点工序A13，因其不是独立工序，不能调整到最佳时刻开始加工，因而影响了综合调度的整体效果。

6 结论

本文在综合调度中，以多工序设备为优化对象，以最小化复杂产品总加工用时和提高设备整体利用率为优化目标，在全面考虑制造系统中产品工艺、加工工序、设备运行情况和工序约束关系等诸多因素基础上，提出了考虑多工序设备权重的资源协同综合调度算法。在纵向优化方面，以优先级和权重值为主的排序策略，有效地减少了工序间的加工空隙；在横向优化方面，最佳调度时刻策略有效地提高了设备利用率，因此算法进一步优化了综合调度效果。同时，也为深入研究复杂产品的综合调度问题拓展了思路，具有一定的理论和实际意义。