哈默斯坦非线性时变系统的加权学习辨识方法

仲国民 俞其乐 陈 强

(浙江工业大学信息工程学院 杭州 310023)

1 引言

非线性特性广泛存在于实际工业生产过程中，为便于研究其变化规律，需要用数学模型来对所研究的物理现象或过程进行定量分析，因此非线性系统辨识问题受到越来越多的关注。非线性系统结构复杂，难以采用统一模型进行描述，在过去的几十年里，国内外学者主要致力于较普遍的块结构非线性系统辨识[1]。块结构非线性系统可以分为非线性静态部分和线性动态部分，分别用非线性函数和线性函数来表示其特性[2]。其中，维纳(Wiener)系统、哈默斯坦(Hammerstein)系统及其组合形式是应用最广泛的配置。哈默斯坦系统广泛应用于模拟连续搅拌釜式反应器、pH中和过程、蒸馏塔、液压自动发电量控制系统、多传感器系统等非线性过程或系统[3,4]。它由1个非线性静态函数串联和1个线性动态子系统构成，其中哈默斯坦受控自回归滑动平均模型(Controlled AutoregRessive Moving Average model, CARMA)系统的具体形式描述如图1所示。

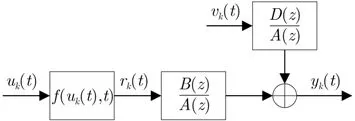
图1 哈默斯坦系统CARMA模型

针对哈默斯坦系统的辨识问题，已开展较多研究工作，如子空间辨识法[5–8]、过参数化法[9,10]、最小二乘法[11]、极大似然法[12]、非参数核回归估计[13,14]、分数阶法[15]、基于特殊输入信号的方法[16]和相关分析方法[17]等。文献[16]提出一种识别哈默斯坦非线性过程的方法，该方法利用一个特殊的测试信号，能够识别出哈默斯坦系统由1个非线性静态函数和1个线性动态子系统组成。针对哈默斯坦非线性带外部输入的自回归滑动平均模型(Autoreg-Ressive Moving Average model with eXogenous Input, ARMAX)，文献[18]提出了一种迭代梯度算法。上述方法均是假设静态非线性特性为子函数多项式的组合前提下，针对定常哈默斯坦系统开展的研究。现有带遗忘因子递推算法[19]、块脉冲函数法[20]等能够提高时变参数跟踪性能；迭代学习辨识算法[21,22]有效解决了时变参数估计问题。鉴于块结构时变非线性系统辨识方面的研究尚少，本文将迭代学习方法进一步运用于基于块结构的非线性系统辨识。

本文提出一种加权迭代学习辨识的方法，其动机是已有系统辨识算法加权修正的思想[23]。当动态系统在有限区间上重复运行时，沿重复轴来看，固定时刻对应的参数是相对固定的，可以采用迭代学习算法估计时变参数。但由于实际中存在非重复初始条件和外部干扰，一致重复运行并不是总能保证的。因此，为提高参数估计精度和系统跟踪效果，将时间轴上加权矩阵方法推广运用于沿重复轴上的修正，构建加权迭代学习算法。

本文考虑有限区间上重复运行的哈默斯坦非线性时变系统，借助哈默斯坦定常系统辨识方法，采用辅助模型方法[24]，推导出哈默斯坦非线性时变系统基于“重复轴”的迭代学习最小二乘算法。同时，为避免数据饱和，引入遗忘因子，推导出带遗忘因子迭代学习最小二乘算法。在此基础上，进一步改进准则函数，引入权矩阵，探索一种加权迭代学习最小二乘(Weighted Iterative Learning Least Squares, WILLS)的辨识方法，并将该算法运用于时变哈默斯坦模型的辨识研究，其优点是达到一定辨识精度的条件下，迭代次数少，输出误差小且稳定性好。

2 问题描述

考虑如式(1)所述有限区间上重复运行的单输入单输出离散时变哈默斯坦系统

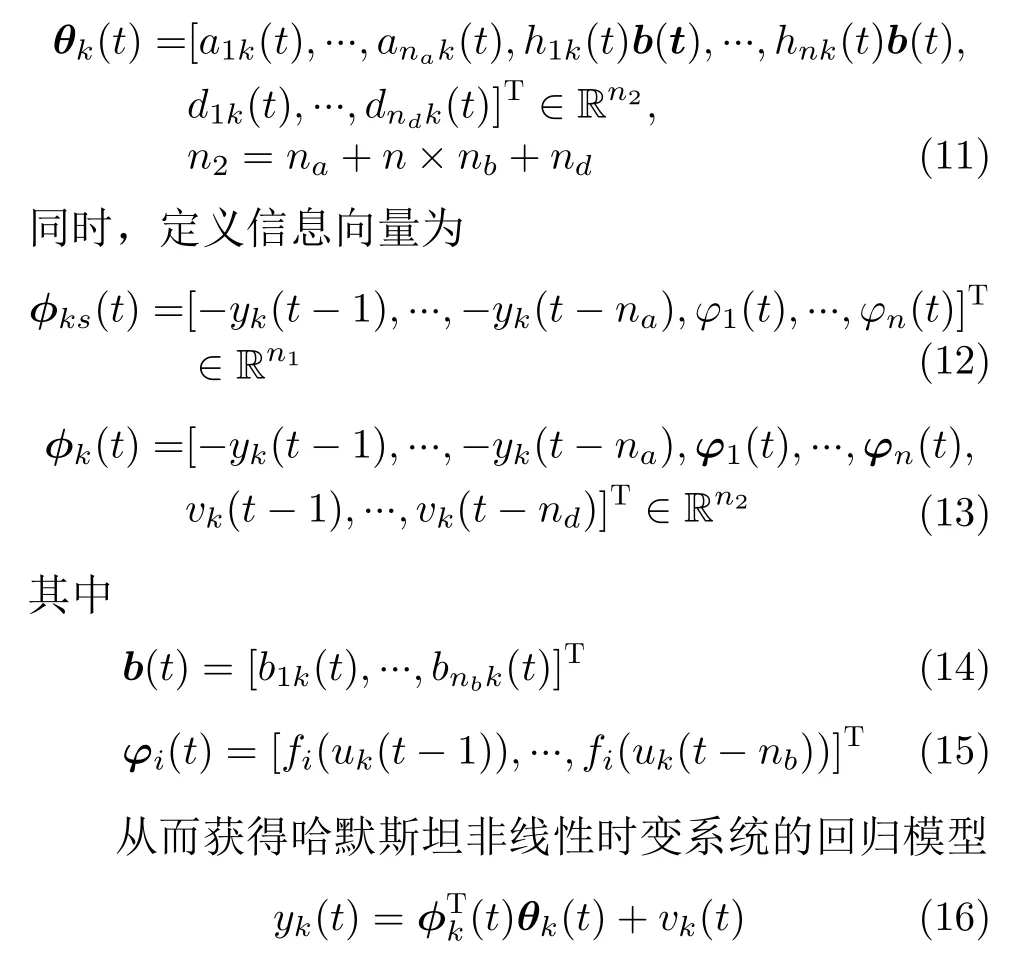
3 哈默斯坦非线性时变系统的加权学习辨识

3.1 迭代学习最小二乘算法

针对重复运行的哈默斯坦时变系统，考虑如式(19)的极小化准则函数

3.2 带遗忘因子的迭代学习最小二乘算法

为避免数据饱和现象，增加新数据的权重，加快跟踪误差收敛速度及精度，在上述算法的基础上引入遗忘因子λ，考虑如式(30)的准则函数

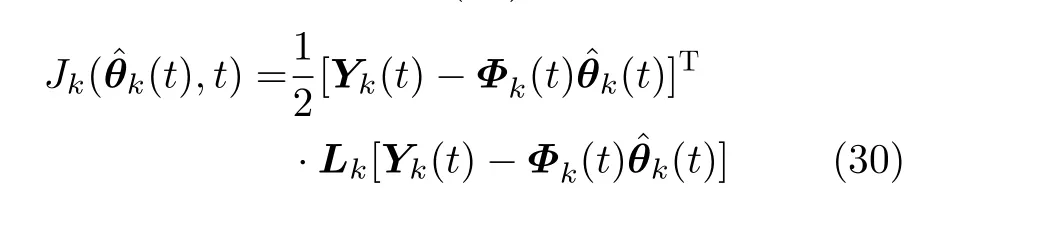
3.3 加权迭代学习最小二乘算法

上述两类算法能获得参数的一致估计，但对初始条件的一致性要求苛刻，且跟踪精度有进一步提升的空间，下面提出一种加权的迭代学习算法以获得更优跟踪效果和辨识精度。为了得到参数θk(t)的估计，考虑如式(40)的准则函数[21]

4 数值算例

表1 采用加权迭代学习最小二乘算法进行参数估计流程图

加权迭代学习算法的参数估计结果如图2所示，3种算法的模型输出误差和参数估计误差如图3和图4所示。仿真结果表明，加权迭代学习算法可以有效估计模型的时变参数。在迭代学习最小二乘算法的基础上引入遗忘因子可以改善模型输出误差和参数估计误差。考虑如式(40)的准则函数，引入加权矩阵，可以进一步降低模型输出误差，提高辨识精度，尤其在达到某一确定的参数估计误差或模型输出误差时，迭代次数明显减少，同时该算法可获得更好的辨识效果。

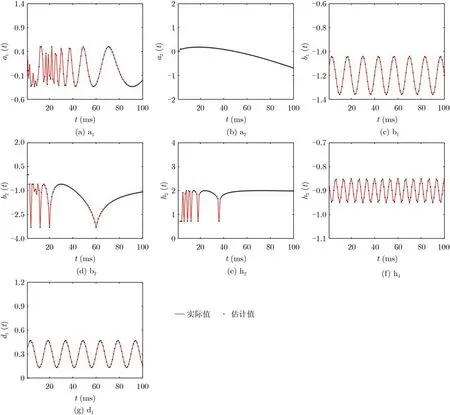
图2 采用加权迭代学习最小二乘算法的参数估计结果

图3 采用3种不同算法的模型输出误差比较

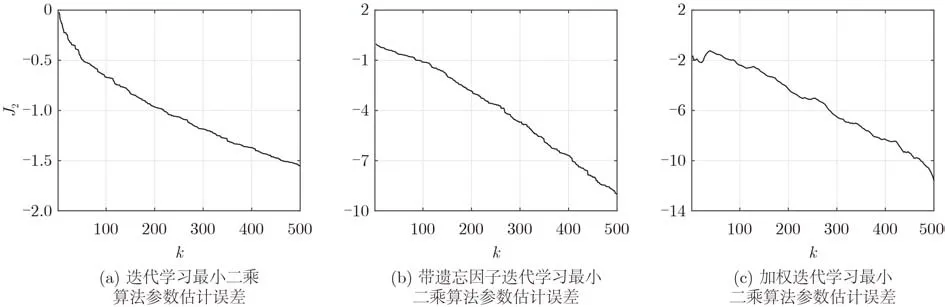
图4 采用3种算法的参数估计误差比较

5 结论

对于Harmmerstein非线性时变系统的参数估计问题，本文提出加权学习辨识算法，推导了重复运行条件下的迭代学习最小二乘法、带遗忘因子迭代学习最小二乘法和加权迭代学习最小二乘法。在重复持续激励条件下，仿真结果显示加权学习辨识算法可以实现时变参数的完全估计。与现有辨识算法相比，本文算法进一步提高了时变参数的估计精度，提高了算法的跟踪性能，在达到一定辨识精度下，加权算法可以减少重复运行的次数。