灵活运算 步步有据——培养小学生运算能力的两点思考

朱 敏 李 鹏

（安徽省凤台县实验小学 南京师范大学苏州实验学校）

数学运算能力是数学三大能力之一，它是数学能力结构中非常重要的一个能力构成。数学运算能力形成的中心环节，是准确把握运算目标，学会根据问题特点及运算的条件选择适当运算途径，形成合理简捷的运算意识和习惯。运算能力欠缺会制约学生数学能力的提高和问题的解决，笔者根据在教学实践中发现的问题，谈两点自己的思考。

一、灵活运算，克服思维定式

所谓思维定式，是指遵循已有的思维活动经验和规律，在反复使用中形成的固定的思维模式、路线、方式、程序。在教学实践中，要使学生运算正确、迅速、合理，势必要使学生掌握运算的思路、法则，通过练习形成运算模式的心理表象，外显形式达到熟练的水平。但与此同时，也就产生了思维定式。

例如，在教学例如“7002－687”这类被减数中间有零的减法时，尽管我们提倡学生在已有知识经验的基础上去探索多种算法和其中蕴含的算理，但由于该题易错，教师仍会不断强调用竖式计算过程中连续退位的方法，接下来经过反复练习达成正确计算的目标。为保证计算出正确的结果，学生在计算时形成一种固定的思路，小心翼翼地列竖式计算，忽略了对其他运算途径的探索与应用。

为使学生能适时摆脱固有的运算模式，对于算式中7002这样特殊的数，我们还可以引导学生用以下技巧来做，通过把7002写成6999+3的形式，可以非常简单地进行计算：

这里的关键在于，如果被减数中有一行“9”，那么做减法时就不需要借位，通过心算可以很容易得到答案。学生如果掌握了其中蕴含的思想方法，可以把计算过程写得更简洁一些，即：

在让学生深刻理解算理、熟练掌握算法的同时，教师应注意训练学生的观察能力，使其能从问题特点入手，对问题进行有效的分解、组合变形，发现获得运算结果的捷径，并能选择合理的运算方法和途径，也能觉察到运算中不合理的地方并及时改进。克服思维定式的消极影响，从旧有的运算桎梏中解脱出来。

二、步步有据，融入演绎推理

在小学生的日常生活中，有很多行为必须符合某种要求。例如：小明上下楼梯，应该靠右行；小红过马路，必须走斑马线等。这些不足为奇的小事，却蕴含着从一般到特殊的演绎推理。以小红过马路来说，她之所以必须走斑马线，是因为交通部门有这样一个规定，所有行人过马路必须走斑马线，这个规定是针对所有人的，所以它是一个一般性要求，而小红是一个特殊的个人，她必须遵守这个规定，所以，她过马路必须走斑马线。我们用下面三句话完整地表述：

1.交通规则规定，所有行人过马路必须走斑马线。

2.因为小红是一个人。

3.所以她过马路必须走斑马线。

第一句话是“一般”，称作“大前提”；第二句话是“特殊”，称作“小前提”；第三句话是“结论”。第三句话是根据第一句话和第二句话推出来的，也就是说，结论是从一般到特殊推出来的，所以小红过马路必须走斑马线这件事情，是从一般到特殊推出来的一个演绎推理。

在日常生活中有许许多多的演绎推理。在数学学习中，演绎推理就更多了，四则运算也不例外。例如：计算

教师可以提醒学生注意从整体上去观察这个算式的特点，联想与之对应的运算律，就会发现它符合乘法分配律a（b＋c）=ab＋ac符号右边的特点，据此作出判断，就得到了简捷的算法。用三段论表述推理过程为：

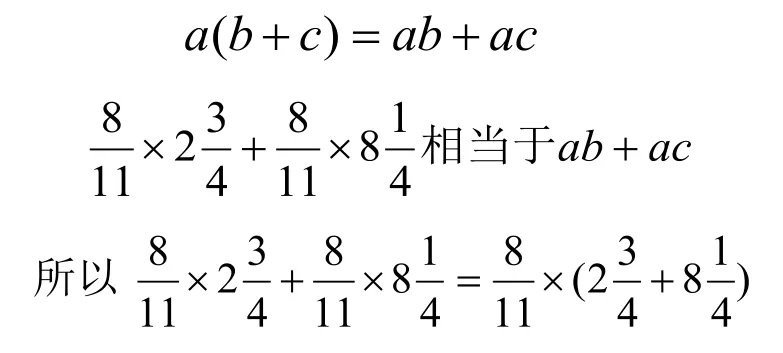
再如：125×8÷125×8（这是各地小学生最常见的运算错误题型之一），结果是64，也是有根据地推出来的。众所周知，四则混合运算有这样一条规定，凡是只有乘法和除法的运算，应该按照从左到右的顺序进行，这是一个一般性的要求，而125×8÷125×8是一个特殊的乘除混合计算题，所以，必须按从左到右的顺序，先做乘法再做除法，最后做乘法。所以：

可见，这也是一个从一般到特殊的演绎推理。如果不按这个规定的顺序，而是先计算两边的乘法再做除法，就会有：

学生仅凭直觉算出这样一个错误的结果，重要原因之一是不知道从一般到特殊的演绎推理，没有主动联想有没有与之相符的运算律、性质或法则，推理后再运算。教师应该向学生展示计算错误过程，使学生感受到：同一道算式，如果是同级混合运算，不同的运算顺序会得到不同的结果，数学中必须有一个大家都要遵守的规定。

另一方面，运算教学中融入演绎推理，更加有利于学生对算理内涵的深刻理解，在运算时做到有理有据，步步有据。例如：计算891÷36。

学生学习竖式，并将竖式改写成横式。

组织学生观察、对比、判断、推理：

第一个判断是“891等于89个十加1个一”，依据是多位数的组成（十进制计数法的位值）。

第二个判断是“89个十里面有20个36，余17个十”。

第三个判断是“17个十加个位的1个一，也就是171里面有4个36，余27”。

这两个判断的依据是“位值”的概念和有余数除法的意义。

最后把两次除的商加起来得24，891里面一共有24个36，余27。

利用竖式计算，实质上只是一种便于计算的书写形式，以上改写和口述既是一个计算过程，也是一个演绎推理的过程，给竖式提供了充分的理论依据。

总之，计算是具体的推理，要把对算理的理解上升到推理的高度、思想方法的高度，才能收到事半功倍的效果。当然，学生在学习这些内容时，演绎推理的运用是隐含在学习过程中的，学生并没有意识到自己在用演绎推理，但数学教师应该清楚这一事实，并有意识地引导学生更完善地用好演绎推理。如果学生能做到每一步演算、每一步证明都能有充分的根据和理由，就可以逐渐具备较高的运算能力。