基于多层前馈神经网络算法的房价预测模型

周麟　郝仁杰　尤权圣

摘要：房地产泡沫问题是影响人民生活质量的一大难题，房价的持续上涨给人民增加了巨大的生活成本。因此，建立准确有效的房价预测模型，对于制定有效政策，精准调控房价，提高人民生活质量具有重要意义。文章主要通过分析住房的需求、供给、地理空间几大方面，得出影响房价的三个主要因素。采用基于遗传算法修正的BP（多层前馈）神经网络算法，利用2012～2019年无锡市三个主要影响因素的数据，建立了基于BP神经网络算法的房价预测模型。

关键词：基于遗传算法修正的BP神经网络算法;线性回归;VAR模型;杜宾模型;灰色关联分析

一、模型的建立与求解

（一）住房需求模型

1.收入弹性

居民的住房需求受到居民收入弹性的影响，收入弹性指的是当住房需求发生变化时，需求变化的百分比与随之变化的城市居民收入的比，收入弹性是人民收入水平对住房需求的影响程度的指标。

2.住房需求函数

设住房需求函数是对数性函数形式，即

ln（H）=β0+β1ln（Y^）+β2ln（Ph）+β3ln（Px）+μ（1）

其中：β1+β2+β3=1：μ函数的误差项;H：居民平均住宅消费量;Y^：居民平均家庭可支配收入;Ph：居民平均住房价格;Px：居民消费价格指数;

由于■■=■，所以β1和β2就分别对应住房需求的收入弹性（Ei）和价格弹性（εi）。Eh=Ph·H，作用于线性变换式（1）可以得到

其中E■为单位时间的住房支出;P■=Ps·Pa，其中（Pa）代表人均建筑价格，（Ps）代表商品房销售价格。

对数据进行处理，进行逐步回归得到线性回归，结果如表1所示：

由表1可以得到相应的回归模型如下：

运用E■=P■·H代入（3）式得：

可见，居民平均住宅消费量与居民平均家庭可支配收入、居民平均住房价格正相关，与居民消费价格指数负相关。

（二）住房供给模型

蛛网模型用来描述市场经济中商品的价格与数量的变化规律，一般而言，本期的商品供给量将受到前两期商品价格的影响，综合分析前两期价格，参照传统预期，近一期价格占大权重，Pt-1、Pt-2分别是前两期价格。也就是说，Pt-1较Pt-2权重更大，设Pt-1权重为γ，Pt-2权重为1-γ，1/2<γ<1，因此得到新的蛛网模型供给方程为：

考虑蛛网模型，本期商品需求量Q■■取决于本期价格Pt，可得出需求函数为Q■■=f（Pt），但考虑到市场的调节功能，得到新的价格关系：

对蛛网模型方程组中进行单个方程的逐步回归，将得到的拟合系数带入方程组，得到新的方程：

对Pt、Pt-1、Pt-2进行回归，得到下式：

因为蛛网模型主要用于近期供给预测，不适合用于长期预测，因此本文另采用向量自回归模型，即VAR模型。

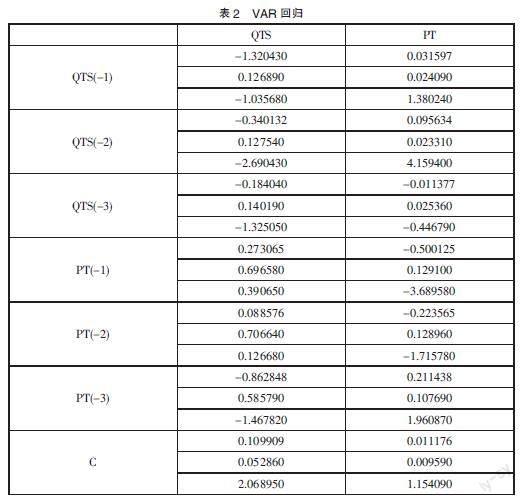
对VAR模型进行逐步回归，得到的回归结果如表2所示：

由此可得VAR模型估计式为：

综合以上模型，可知往期房价会很大程度上影响到当期的商品房供给量。

（三）空间模型

本文假设政府对于土地财政的政策对房价具有影响，为此，本文建立如下模型，为了将异方差和量纲影响降到最低，对于非比例变量，本模型进行化对数处理：

ln（yit）=α+β1lnlfit+β2git+β3lnzit+ρWityit+μ1Wijlfit+μ2Wijgzit+μ3Wijlnzit+εit（10）

其中，lny为居民住房价格;ρWy为周边城市房价对本市房价的影响，其中W为空间权重，ρ为空间相关系数，X为解释变量，α为常数项，β为解释变量的系数矩阵;θWx为周边城市的解释变量空间溢出对本市房价的影响，θ表示影响系数。μit是随机误差项。

模型回归结果如表3所示。

在直接效应方面，对房价具有重要影响的因素是城镇居民可支配收入、土地财政、房地产开发投资金额、住宅低价。在其他因素不发生变化的前提下，当土地财政有1%的增加时，房价将产生0.0002%的增长。住房用地价格对房价具有正向的促进作用。此外，开发商的投资积极性会随着房地产开发投资额提高而提高，从而推升房价，因此房地产开发投资额对房价也具有重要的正向促进作用。同时，由于收入水平的增加意味着消费者支付能力的提升，需求产生的拉动作用将会带动房价上涨，城镇居民可支配收入这一因素对于房价也有促进作用。上述众多因素中，住宅用地的价格对于房价而言其作用效果不显著。

间接效应上，土地财政这一因素对于相邻城市房价具有明显的正向溢出效应，它通过转让土地取得收入，从而增加了开发商的拿地成本，导致相邻城市房价的上涨。同时，住宅用地的供给对相邻城市房价具有正向空间溢出作用，增加住宅用地供应，由于政府住宅用地供应有限，土地资源稀缺，开发商疯狂抢占土地，导致周边城市房价上涨。对房价具有正向溢出效应的还有城镇居民可支配收入，居民收入水平的提高也增加了居民到邻近城市购房的支付能力，从而刺激邻近城市房地产市场的供需状态。

二、城市房价预测

由上述分析，设因子集为X1，X2，X3，……则定义关联系数函数为

依据近几年来的数据，本文构建了各因素与房价的相关系数，得到居民家庭收入（X1），往年的房价（X2），居民消费价格指数（X3）以及城市年GDP（X4）是与房价关系紧密的几个因素，它们所对应的关联系数分别是0.99617、0.95901、0.91458、0.90378。

基于以上分析，可采用BP神经网络算法建立房价的预测模型。

本文选取2012～2019年居民家庭收入、去年房价、居民消费价格指数以及城市年GDP作为数据进行输入，通过训练BP神经网络模型并利用该模型进行房价的滚动预测，具体是利用第一年和第二年的数据进行训练并对第三年的房价进行预测。共采用8组输入数据，其中6组数据分别作为6个输入层神经元的训练样本，2组数据作为测试样本，共设置15个隐含层神经元，阈值和初始权值采用的均是系统默认值。无锡市的2012～2019年居民家庭收入、去年房價、居民消费价格指数以及城市GDP如表4所示。

根据神经网络的预测结果，制作预测房价与实际房价对比图1。

由图1可见，使用基于遗传算法修正的BP神经网络模型，利用居民家庭收入、去年房价、居民消费价格指数与城市年GDP对房价做出的预测是十分准确的。

参考文献：

[1]郑思齐，刘洪玉.住房需求的收入弹性：模型、估计与预测[J].土木工程学报，2005，38（07）：320-324.

[2]林祖嘉，林素善.台湾地区住宅需求价格弹性与所得弹性之估计[J].住宅学报，台湾住宅学会，1994（02）：25-48.

[3][日]雨宫健著，朱保华，周亚虹，等译.高级计量经济学[M].上海：上海财经大学出版社，2010：10-16.

[4]李光勤，蛛网模型中的价格稳定性分析[J].浙江万里学院学报，2007，20（02）：17-19.

[5]么海涛.蛛网模型的数学研究[J].北京信息科技大学学报，2011，26（02）：96-98.

[6]张克毅.基于灰色系统理论的推荐算法研究[D].重庆：重庆邮电大学，2018.

（作者单位：江南大学物联网工程学院）