开口断面桥梁颤振稳定性及优化措施机理研究

董国朝 许育升 韩艳 蔡春声 李凯

摘要：基于数值计算方法研究了开口断面主梁的颤振稳定性及下稳定板的作用机理.通过对比风洞试验的三分力及颤振临界风速结果，验证数值计算方法的可靠性，借助流场可视化直观地分析了颤振机理及下稳定板的抑制机理.结果表明：来流在上游栏杆、上游箱室底板及下检修道处分离形成旋涡并向下游发展，期间产生与桥断面运动方向相同的气动力，成为颤振发散主导因素.在桥梁断面增设下稳定板能形成稳定的旋涡，气动力总体做负功，有效地抑制了颤振发散.增设1/4下稳定板，稳定板间形成了稳定的旋涡，气动力在运动周期内持续做负功，而同时增设下中央稳定板和1/4下稳定板在上游检修道与稳定板间形成的旋涡与上表面的旋涡交替主导气动力的方向，气动力先做负功后做正功再做负功.故只增设1/4下稳定板相比同时增设1/4下稳定板和下中央稳定板更有利于改善主梁的颤振稳定性能.研究结果能给同类型桥梁断面颤振抑振措施的选取提供参考.

关键词：数值计算;颤振稳定性;气动措施;开口断面;下稳定板

中图分类号：U441.3       文献标志码：A

Study on Flutter Stability and Mechanism of Optimization Measure for Open-cross-section Girder

DONG Guochao1，XU Yusheng1，HAN Yan1?，CAI Chunsheng1，2，LI Kai1

（1. School of Civil Engineering，Changsha University of Science & Technology，Changsha 410114，China;

2. Louisiana State University，Baton LA70803，Louisiana，USA）

Abstract：The mechanism of flutter stability of open-cross-section and lower stabilizers are studied by numeri ? cal calculation. The reliability of the numerical method is verified by comparing the wind tunnel test results of aerody ? namic force coefficients and critical flutter wind speed. The mechanism of flutter instability and the suppression mechanism of lower stabilizers are analyzed intuitively by visual flow field. The results show that the incoming flow is separated from the upstream railing， the upstream of box room bottom and the lower inspection access road. Vortices are formed upstream and developed downstream of the girder. During this period， the aerodynamic force with the same motion direction as the girder is generated， which becomes the dominant factor of flutter divergence. The lowerstabilizers are added to the girder to form stable vortices on the lower surface， which effectively suppresses the flutter divergence. By adding 1/4 lower stabilizers， stable vortices are formed between the stabilizers， and the aerodynamic force continues to do negative work in the motion cycle. However， by adding the lower central stabilizer and 1/4 lower stabilizers at the same time， the vortices formed between the upper inspection access road and the stabilizers alter? nately dominate the direction of aerodynamic force with the vortex on the upper surface. Aerodynamic forces do nega? tive work first， then positive work and eventually negative work in the motion cycle. Flutter stability of the girder is more beneficial to be improved by adding only 1/4 lower stabilizers than adding both 1/4 lower stabilizers and lower central stabilizers. The research results can provide a reference for the selection of flutter suppression measures of the same type of girder.

Key words：numerical simulation;flutter stability;aerodynamic measures;open-cross-section;lower stabilizers

开口断面主梁因其具有良好的受力性能、吊装简便及造价低等优点，常使用于双索面体系的大跨度悬索桥及斜拉桥中.颤振及涡振对主梁的气动外形十分敏感，开口形式的钝体主梁断面因气动性能不稳定，在不进行气动优化情况下，易出现明显的涡振和颤振现象[1-2].同时，部分学者在开口断面主梁上也发现了软颤振现象[3-5].

目前，国内外许多文献对开口断面主梁的气动性能均有所报道[6-9].董锐等[8]对斜拉桥Π型开口断面主梁进行气动选型，研究了Π型开口断面主梁的气动外形对涡振和颤振的影响.当主梁断面自身空气动力学性能无法满足抗风要求时，一般需要通过增设气动措施来改善主梁的气动稳定性，使其满足抗风要求，保证桥梁在施工及使用过程的安全.钱国伟等[9]通过节段模型风洞试验研究栏杆、风嘴及水平隔流板等气动控制措施对斜拉桥Π型开口断面主梁涡激共振的控制效果. Irwin[10]介绍了底部隔板对开口断面主梁的气动抑制效果.

下稳定板是用于改善开口断面主梁气动稳定性常见的气动措施之一，张志田等[11]对某大跨斜拉桥的开口断面主梁增设气动措施进行节段模型试验，试验结果发现下稳定板能有效抑制主梁的涡振.董佳慧等[3]对开口断面边箱钢-混叠合梁开展了系列气动措施研究，发现增设稳定板能改善边箱钢-混叠合梁的颤振性能，但作用效果有限.郑史雄等[5]在开口断面主梁发现软颤振现象，认为在开口断面主梁设置下中央稳定板对软颤振性能的影响不明显.随着计算机技术的快速发展，计算流体动力学（Compu? tational Fluid Dynamics，CFD）也逐渐成为桥梁风致振动问题的研究手段之一，许多学者借助 CFD对桥梁的风致振动问题展开了大量研究[12-14].周志勇等[15-16]采用离散涡方法对开口断面桥梁绕流问题开展了数值模拟研究，CFD 结果与试验值吻合良好并进一步分析了颤振抑振措施的机理.杨光辉等[1]结合风洞试验和 CFD模拟发现下稳定板能改善Π型开口断面主梁的气动稳定性.战庆亮等[2，17]结合风洞试验及 CFD 方法对开口断面主梁开展了研究，结果表明在开口断面桥梁下表面增设下稳定板能显著提高颤振临界风速.杨詠昕等[18]总结了被动气动颤振控制方法对三类主梁（闭口钢箱梁、带挑臂箱梁及开口边主梁）的控制效果，认为中央稳定板能显著提高三类主梁的颤振稳定性能且控制效果与稳定板的位置和高度有关.以上研究对开口断面主梁气动性能及下稳定板的气动优化作用均有所总结，但由于下稳定板高度及设置的位置不同，且每一座桥的气动外形及桥上的附属设施也不尽相同，所以下稳定板对主梁气动稳定性的改善效果也不一，下稳定板设置的位置对开口断面主梁颤振的抑制机理尚不明确.

本文以某开口断面主梁的大跨悬索桥为工程背景，通过对比风洞试验的三分力系数结果验证网格无关性及时间无关性，对比颤振计算结果进一步确定数值计算方法的可靠性，从流场的角度直观地分析原设计开口断面颤振发散原因及不同位置增设下稳定板的抑制效果，研究结果为同类型开口断面桥梁颤振抑振措施的选取提供参考.

1风洞试验概况

对某加劲梁断面形式为开口钢-混凝土结合梁的大跨悬索桥[19]（主跨为838 m）进行节段模型颤振试验，加劲梁断面及部分颤振气动优化措施如图1   比为1∶50，试验主要动力特性参数如表1所示.

原加劲梁断面颤振试验结果表明：+3°攻角下颤振临界风速为31 m/s，低于颤振检验风速，不满足抗风要求[20].为满足颤振稳定性要求，在原设计加劲梁断面增设下中央稳定板和1/4下稳定板（桥梁横断面开口宽度1/4L 处及1/2L 处，稳定板下缘与检修轨道高度平齐）等多种气动措施进行节段模型颤振试验.

2 网格无关性及时间无关性测试

为了保证精度又兼顾计算效率，网格采用分域绘制的方法[14，21-22]，将计算域划分为静网格域、动网格域及刚性域.在断面附近设置一个“刚性域”，主梁断面运动时，刚性域与主梁断面同步发生运动.刚性域内包括边界层以及相应的网格加密，目的是保证桥梁断面周围具有足够的网格精度，以更好地捕捉旋涡的分离和再附.湍流模型采用大涡模拟 Large Eddy Simulation-2d，压力-速度耦合采用 SIMPLEC 算法，整体网格及计算域如图2所示，虚线框内分别为原设计、优化方案1及优化方案2的局部网格示意图，阻塞率小于3%.

在保证计算准确的前提下兼顾计算效率，对网格和时间步进行无关性测试.靠近壁面层第一层网格高度分别取0.04 mm 和0.01 mm，网格数量分别为203996和451415，近壁面第一层网格的YPlus值分别约为0.7和0.2.时间测试步长分别为0.0010 s、0.0005 s 和0.0001 s，以原设计成桥态桥梁断面0°攻角的三分力系数结果为参考来验证网格及时间步长的无关性，测试结果如表2所示.三分力系数定义如下：

式中：CD 是阻力系数;CL 是升力系数;CM 是扭矩系数.模型宽度 B 取0.664 m;模型高度 H 取0.056 m;风速 U 取10 m/s;空气密度ρ取1.225 kg/m3.

网格无关性及时间无关性测试结果表明，原设计成桥态0°攻角下，网格数量为451415和203996的网格在0.0010 s、0.0005 s 及0.0001 s 的時间步长时三分力系数计算结果与风洞试验值吻合良好，网格稳定性良好.综合考虑计算精度和效率，选取时间步长为0.0010 s、数量为203996的网格进行后续其他风攻角三分力系数及颤振分析，网格近壁面YPlus值如图3所示.

图4为成桥态-5°～+5°风攻角下三分力数值模拟结果与风洞试验结果对比图.数值模拟结果与风洞试验结果吻合良好，该数值模拟方法能反映主梁断面的绕流特性，其中，扭矩系数数值模拟结果与风洞试验结果最为接近.

3 颤振稳定性结果对比

节段模型颤振试验结果表明原设计方案的颤振稳定性能较差，不满足规范要求，需采取气动优化措施进一步提高颤振临界风速.风洞试验采取的气动措施包括设置1.4 m、1.5 m 高的上中央稳定板及不同位置的下稳定板.试验结果发现：上、下稳定板均能提高加劲梁断面的颤振临界风速，但上中央稳定板的提高效果较不明显;而在原加劲梁断面设置下中央稳定板和1/4下稳定板的气动措施及其组合措施能较好改善加劲梁的颤振稳定性.风洞试验和数值模拟的颤振临界风速结果如表3所示，原设计断面及优化方案颤振临界风速的风洞试验结果和数值模拟结果吻合较好，数值模拟相比风洞试验的颤振临界风速值整体偏低，在原设计的+3°风攻角上出现最大误差为5.7%.根据抗风规范[20]，当扭转位移标准差达到0.5°时，表明颤振失稳.

风洞试验结果及数值模拟结果均为扭转发散，未发现竖向发散现象，限于篇幅，仅给出最不利风攻角（+3°攻角）下原设计断面、优化方案1及优化方案2的部分工况数值模拟结果的扭转位移时程图，如图5所示.

原设计断面+3°攻角相比0°攻角和-3°攻角的颤振稳定性较差，与文献[2，5]的结果趋势一致，故对原设计断面+3°攻角（最不利攻角）进行优化.风洞试验结果及数值模拟结果表明：优化方案1和优化方案2均有利于改善加劲梁的颤振稳定性.优化方案1相比优化方案2多设置了下中央稳定板，反而降低了加劲梁的颤振临界风速，因此，有必要通过数值模拟可视化流场进一步探讨该开口断面桥梁的颤振发散机理及下稳定板的抑制机理.

4机理分析

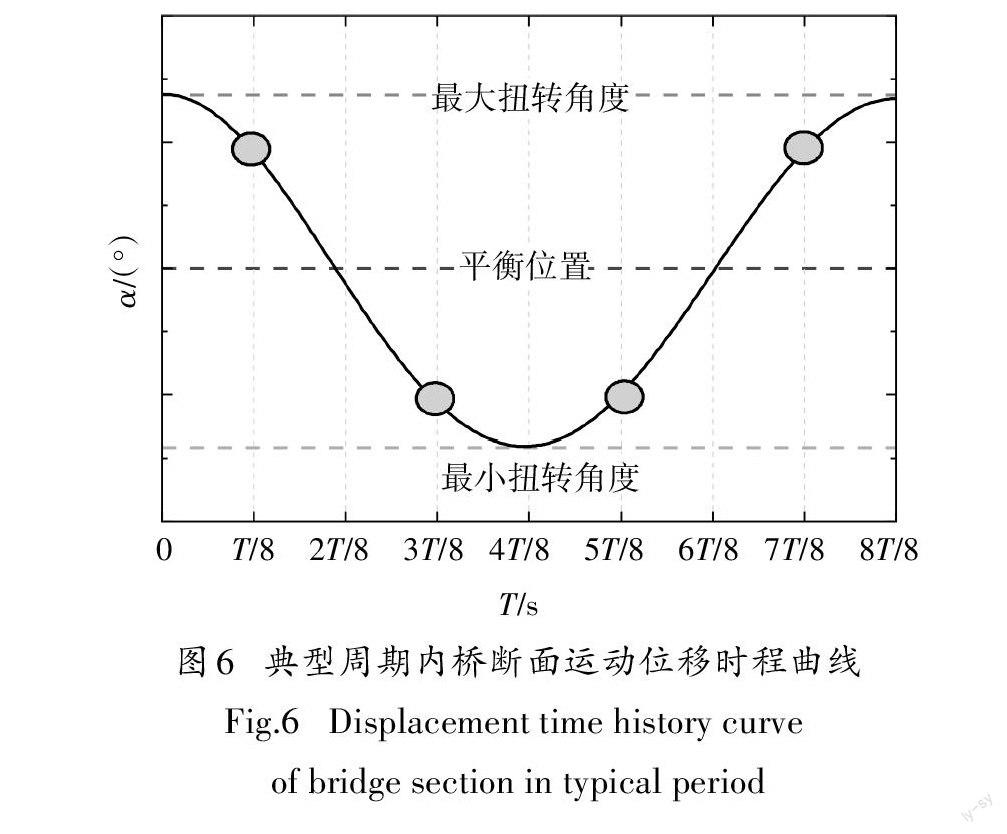
取桥梁断面的一个典型运动周期进行分析[17]，位移时程曲线如图6所示，着重分析 T/8（从最大扭转角度位置运动至平衡位置过程）、3T/8（从平衡位置运动至最小扭转角度位置过程）、5T/8（从最小扭转角度位置运动至平衡位置过程）和7T/8（从平衡位置运动至最大扭转角度位置过程）时刻桥断面附近的流动特性及流场演变过程.

4.1原设计断面颤振发散机理

由表3可知，原设计桥梁断面+3°攻角下，数值计算的颤振临界风速为8.6 m/s，故选取风速分别为8 m/s（未发生颤振）及8.8 m/s（发生颤振）时刻的一个典型运动周期为研究对象，通过桥断面附近压强的变化及流场演变分析颤振发生机理，如图7～8所示.先由压力云图判断上下游气动力方向，若压力云图无法清楚判断气动力方向，则进一步分析速度流线图的旋涡、涡的尺度及其演变判断气动力的方向，图中实心箭头为桥梁断面运动方向，空心箭头为流场对桥梁断面产生的气动力的方向.

成桥态+3°攻角下，风速为8 m/s 时，桥梁断面未发生颤振失稳，一个典型运动周期的压力云图及流线图如图7所示.来流风作用下，在桥梁断面下表面，气流在桥梁断面上游箱室尾部及上游下檢修道处产生分离，形成旋涡脱落，少量小涡在上游箱室及检修道间盘旋.在桥断面上表面，气流在上游栏杆分离，形成旋涡向下游发展，一直运动到尾部脱落.桥梁断面上游的上下表面旋涡相近，总体下表面压强略大于上表面. T/8及3T/8时刻，桥梁断面做顺时针扭转运动.在桥断面上游，气流在风嘴处分离形成大的旋涡使得上表面受负压，下表面交替出现小的正负压区.在桥断面下游，上表面受到上游发展下来的涡的影响，上表面呈负压，下表面均为正压，压差作用下形成竖直向上的气动力，气动力方向与桥梁断面运动方向相反，做负功，耗散振动系统的能量.5T/8及7T/8时刻，桥梁断面做逆时针扭转运动.在桥断面下游，桥梁断面下游上表面虽存在较大的涡，但下表面也存在许多小涡，在下游靠近形心处，上下表面压强较为均衡.在桥梁断面上游，上表面为负压绝对值较大，且下表面基本为正压，上表面涡的尺度略大于下表面.在压差作用下，气动力在上游处方向向上，与桥梁断面的运动方向相反，做负功，耗散振动系统的能量.低风速下，气动力方向与桥断面运动方向相反，气动力在运动过程中做负功，消耗系统能量，桥梁断面未出现颤振失稳现象.

图8为成桥态风速为8.8 m/s 时桥梁断面的一个典型运动周期内部分时刻的压力云图.对比图7可以看出，在高风速下，负压区压强绝对值进一步增大，整个流场的旋涡愈加丰富.T/8和3T/8时刻，桥梁断面做顺时针扭转运动，在桥断面上游，上下表面的旋涡相近，上表面基本为负压，下表面正压占主导，气动力在上游区的方向为竖直向上，与桥梁断面的运动方向相同;在桥断面下游，虽然上表面为负压，下表面为正压，但在箱梁尾部下表面处存在压强绝对值较大的负压区，且对桥断面形心的作用力矩较大，故气动力在下游方向为竖直向下，与桥断面的运动方向相同，气动力做正功，增大系统能量.5T/8和7T/8时刻，桥梁断面做逆时针扭转运动，在桥断面上游，上下表面的旋涡相近，上表面呈现负压，下表面存在正负区，气动力在上游的方向竖直向上;在桥梁断面下游，下表面出现少量涡，上表面存在较大的涡，下游主要受上表面大涡的影响，桥断面上表面基本成负压，气动力在下游的方向竖直向上，但下游上表面的负压小于上游的，下表面正压大于上游的，故下游的气动力大于上游，总的气动扭转方向与桥梁的运动方向相同，气动力做正功，增大系统能量.高风速下，气动力方向与桥断面运动方向相同，气动力做正功，增大系统能量，故桥梁断面发生了颤振失稳.

限于文章篇幅，本文仅给出+3°攻角下，风速为8.8 m/s 时成桥状态的位移时程及气动力矩累积功 W 随时间变化图，如图9所示.随着扭转振幅的增大，气动力做功总体上呈增大趋势，气动力持续做正功，与图8的结果一致.进一步结合图7和图8，在较低风速即8 m/s 下，气动力做负功，方向与桥梁的运动方向相反，桥梁断面未出现颤振发散现象;在较高风速即8.8 m/s 下，气动力做正功，气动扭矩方向与桥梁断面的运动方向相同，增大系统能量，桥梁断面发生颤振失稳.

4.2增设1/4下稳定板抑制机理

由风洞试验及颤振数值模拟结果可知，在原设计桥断面下表面增设1/4下稳定板（优化方案2）能显著提高主梁的颤振临界风速.为探讨1/4下稳定板对颤振的抑制机理，通过对比+3°攻角下8.8 m/s 时原设计断面与优化方案2的流场来进一步分析.

图10为来流风速为8.8 m/s 时增设1/4下稳定板（优化方案2）桥断面在一个典型周期的压力云图及速度流线图.对比图8发现，增设1/4下稳定板后，上游箱室与下稳定板间及两下稳定板间形成了稳定的旋涡，下游下稳定板与箱梁间的旋涡较小，桥断面上下表面的压力差减小，整个流场趋于稳定.

T/8及3T/8时刻，桥梁断面做顺时针扭转运动，桥断面的上下表面交替出现正负压区域，桥断面附近压强较为复杂.流线图表明，两块下稳定板间主梁上下表面的旋涡尺度相近.在桥断面上游，箱梁与下稳定板间存在大量的负压为主的旋涡，而上表面的旋涡主要以正压为主，因此，气动力在桥断面上游的方向为竖直向下，与桥断面的运动方向相反;在桥断面下游，尾部箱梁与下稳定板间旋涡量较少，且上表面存在一个较大的负压区，气动升力在断面下游的方向为竖直向上，气动力扭矩方向与桥断面的运动方向相反，做负功，耗散振动系统的能量.5T/8及7T/8时刻，桥梁断面做逆时针扭转运动，桥断面上下表面的旋涡尺度相近.在桥断面上游，桥断面附近总体表现为下表面正压，上表面负压，气动力在上游方向为竖直向上，与桥断面的运动方向相反;在桥断面下游，上下表面流场较为复杂，体现为正负交替的压强区，上下表面总的压力值较为平衡，气动扭矩与桥断面运动方向相反，气动扭矩做负功，消耗整体系统的能量.

来流风在桥断面上表面的栏杆处分离，并形成旋涡脱落，增设1/4下稳定板后，在桥断面下表面的上游及两下稳定板间形成了稳定的旋涡区，整体流场相对更为稳定.在桥断面运动过程中，气动扭矩的方向与桥梁运动方向相反，气动力做负功，消耗了系统的能量，未出现颤振失稳现象.

4.3增设1/4下稳定板和下中央稳定板的抑制机理

由风洞试验及颤振数值模拟结果可知，在原设计桥断面下表面同时增设1/4下稳定板和下中央稳定板（优化方案1）能有效地提高主梁的颤振临界风速，但优化方案2的作用效果更为明显.为明确该作用效果及其差异，进一步对比+3°攻角下8.8 m/s 时原设计断面、优化方案2与优化方案1的流场来进一步分析.

图11为+3°攻角、来流风速为8.8 m/s 时同时增设1/4下稳定板及下中央稳定板（优化方案1）桥断面在一个典型周期的压力云图.对比图8可以发现，增设1/4下稳定板及下中央稳定板后，桥断面下表面多处形成了稳定的旋涡，旋涡分布较为均衡.进一步对比图10可以发现，在优化方案2的基础上增设下中央稳定板后，上游检修道与稳定板间形成了一个负压值较大的旋涡，成为气动力的主导因素.

T/8和3T/8时刻，桥梁断面做顺时针扭转运动.在桥断面上游，检修道与下稳定板间形成一个大的负压旋涡，气动力在桥断面上游的方向为竖直向下，与桥断面的运动方向相反;在桥断面下游，上表面栏杆分离的旋涡发展到下游形成较大的旋涡，导致下游上表面压强低于下表面，气动力在桥断面下游的方向为竖直向上，气动扭矩的方向与桥断面运动方向相反，气动力做负功，耗散了振动系统的能量.5T/8时刻，桥断面做逆时针转动.在桥断面上游，检修道与下稳定板间的旋涡依旧存在，下稳定板间形成了正压区，上下表面的压力较为平衡;在桥断面下游，下表面均为负压且压力数值较大，上表面同时存在着正负压区，下表面压强明显小于上表面，气动力在桥断面下游方向向下，气动扭矩与桥断面的运动方向相反，气动力做负功，耗散了振动系统的能量.7T/8时刻，桥梁断面做逆时针扭转运动.在桥断面上游，两个下稳定板间的正压削弱，检修道与下稳定板间的旋涡成为气动力的主导，气动力在桥断面上游的方向为竖直向下，与桥断面的运动方向相同;在桥断面下游，上表面尾部存在一个较大的负压区，气动力在桥断面下游的方向为竖直向上，气动扭矩的方向与桥断面的运动方向相同，气动力做正功，系统能量增加.气动力在整个周期内做功的总值仍为负，总体上消耗了系统能量，抑制了颤振发散.

4.4优化措施的抑制机理对比分析

相比只增设1/4下稳定板的优化措施，同时增设1/4下稳定板及下中央稳定板后，上游检修道与稳定板间形成了一个负压很大的旋涡，与上表面的旋涡成为气动力的主导因素. T/8、3T/8及7T/8时刻，上游检修道与稳定板间的旋涡起主导作用，气动扭矩的方向为逆时针;5T/8时刻，由于旋涡的脱落，下游下表面的压力减小，桥断面上游的两个下稳定板间的压力增强，气动扭矩方向为顺时针.在桥断面运动的一个周期内，同时增设1/4下稳定板及下中央稳定板的优化断面在 T/8、3T/8和5T/8时刻气动力做负功，7T/8时刻气动力做正功，气动力做功的总值仍为负，总体上消耗了系统能量，抑制了颤振发散.而只增设1/4下稳定板在整个周期内气动力均做负功，更有利于提高颤振临界风速，这与风洞试验及数值模拟结果相符合.

5结论

对某开口断面桥梁的颤振稳定性进行了数值模拟研究，數值模拟三分力结果及颤振临界风速结果与试验结果吻合良好，验证了数值模拟结果的可靠性，通过数值模拟可视化流场分析颤振发散机理及优化措施的抑制机理.结论如下.

1）探明了开口断面桥梁的颤振发生机理：低风速下，下检修道与上游箱室之间的旋涡及上表面旋涡形成的气动扭矩方向与桥梁断面运动方向相反，气动力做负功，抑制了颤振发散;高风速下，由上表面旋涡主导的气动扭矩方向与桥断面运动方向相同，气动力做正功，促进桥梁断面的颤振发散.

2）在开口断面桥梁下表面增设下稳定板能有效地提高颤振临界风速，作用的效果受稳定板位置及数量影响.增设1/4下稳定板后，在桥断面下表面的上游及两下稳定板间形成了稳定的旋涡区，气动力在周期内做负功，改善了颤振稳定性能.

3）同时增设1/4下稳定板及下中央稳定板的措施增强了下表面上游检修道与稳定板间的旋涡，形成了较强的负压区.气动力在周期内既做了正功也做了负功，但整个周期内总功仍然为负，消耗了系统能量，抑制了颤振发散，但效果相比较只增设1/4下稳定板情形不明显.

参考文献

[1] 杨光辉，屈东洋，牛晋涛，等.π型截面涡激振动风洞试验及气动抑制措施研究[J].石家庄铁道大学学报（自然科学版），2015，28（1）：34-39.

YANG G H，QU D Y，NIU J T，et al. Researches on π-section vortex-induced vibration wind tunnel testing and aerodynamic sup ? pression measures[J]. Journal of Shijiazhuang Tiedao University （Natural Science Edition），2015，28（1）：34-39.（In Chinese）

[2] 战庆亮，周志勇，葛耀君.开口叠合梁断面气动性能的试验研究[J].桥梁建设，2017，47（1）：17-22.

ZHAN Q L，ZHOU Z Y，GE Y J. Experimental study of aerody? namic performance of open cross sections of composite girders[J]. Bridge Construction，2017，47（1）：17-22.（In Chinese）

[3] 董佳慧，周强，马汝为，等.边箱钢-混叠合梁颤振性能及气动措施研究[J].振动与冲击，2020，39（3）：155-160.

DONG J H，ZHOU Q，MA R W，et al. Flutter performance and aerodynamic measures of a suspension bridge with side box steel- concrete composite girder[J]. Journal of Vibration and Shock，2020，39（3）：155-160.（In Chinese）

[4]  TANG Y，HUA X G，CHEN Z Q，et al. Experimental investigation of flutter characteristics of shallow Π section at post-critical regime[J]. Journal of Fluids and Structures，2019，88：275-291.

[5] 郑史雄，郭俊峰，朱进波，等.П型断面主梁软颤振特性及抑制措施研究[J].西南交通大学学报，2017，52（3）：458-465.

ZHENG S X，GUO J F，ZHU J B，et al. Characteristics and sup? pression neasures for soft flutter of main girder with П-shaped cross section[J]. Journal of Southwest Jiaotong University，2017，52（3）：458-465.（In Chinese）

[6]  YOSHINOBU K，KICHIRO K，KENSUKE S，et al. Aerodynamicperformance of improved shallow π shape bridge deck[J]. Journal of Wind Engineering and Industrial Aerodynamics ，2002，90（12）：2113-2125.

[7]  YOSHINOBU K，KENJI S，EIKI Y，et al. Improvement of aeroelastic instability of shallow π section[J]. Journal of Wind Engineer? ing and Industrial Aerodynamics，2001，89（14）：1445-1457.

[8] 董锐，杨詠昕，葛耀君.斜拉桥Π型开口断面主梁气动选型风洞试验[J].哈尔滨工业大学学报，2012，44（10）：109-114.

DONG R，YANG Y X，GE Y J. Wind tunnel test for aerodynamic selection of Π shaped deck of cable-stayed bridge[J]. Journal of Harbin Institute of Technology，2012，44（10）：109-114.（In Chi? nese）

[9] 钱国伟，曹丰产，葛耀君.Ⅱ型叠合梁斜拉桥涡振性能及气动控制措施研究[J].振动与冲击，2015，34（2）：176-181.

QIAN G W，CAO F C，GE Y J. Vortex-induced vibration perfor? mance of a cable-stayed bridge with Ⅱ shaped composite deck and its aerodynamic control measures [J]. Journal of Vibration and Shock，2015，34（2）：176-181.（In Chinese）

[10] IRWIN P A. Bluff body aerodynamics in wind engineering[J].Journal of Wind Engineering and Industrial Aerodynamics，2008，96（6/7）：701-712.

[11]张志田，卿前志，肖玮，等.开口截面斜拉桥涡激共振风洞试验及减振措施研究[J].湖南大学学报（自然科学版），2011，38（7）：1-5.

ZHANG Z T，QING Q Z，XIAO W，et al. Vortex-induced vibra? tion and control method for a cable-stayed bridge with open cross section [J]. Journal of Hunan University （Natural Sciences），2011，38（7）：1-5.（In Chinese）

[12]刘志文，洪涵，梁立农，等.广东江顺大桥抗风性能试验研究[J].湖南大学学报（自然科学版），2015，42（3）：112-119.

LIU Z W，HONG H，LIANG L N，et al. Experimental nvestigation of the wind-resistant performance of Jiang-Shun bridge in Guang? dong[J]. Journal of Hunan University （Natural Sciences），2015，42（3）：112-119.（In Chinese）

[13]祝志文，陈政清，顾明.理论平板及其中央开槽颤振特性的CFD 研究[J].湖南大学学报（自然科学版），2006，33（5）：16-20.

ZHU Z W，CHEN Z Q，GU M. Studies on flutter behaviors of ITP and slotted ITP by using CFD simulations[J]. Journal of Hunan University （Natural Sciences），2006，33（5）：16-20.（In Chinese）

[14]祝志文，夏昌.基于两种湍流模型的桥梁颤振导数识别研究及比较[J].湖南大学学报（自然科学版），2010，37（11）：6-11.  ZHU Z W，XIA C. Comparative study of two turbulence models based on the identification of flutter derivatives of bridges [J]. Journal of Hunan University （Natural Sciences），2010，37（11）：6-11.（In Chinese）

[15] CHEN A R，ZHOU Z Y，XIANG H F. On the mechanism of vertical stabilizer plates for improving aerodynamic stability of bridges [J]. Wind and Structures，2006，9（1）：59-74.

[16]周志勇，陈艾荣，项海帆.涡方法用于桥梁断面气动导数和颤振临界风速的数值计算[J].振動工程学报，2002，15（3）：83-87.

ZHOU Z Y，CHEN A R，XIANG H F. Numerical assessment of aerodynamic derivatives and critical wind speed of flutter of bridge decks by discrete vortex method[J]. Journal of Vibration Engineer? ing，2002，15（3）：83-87.（In Chinese）

[17] 战庆亮，周志勇，葛耀君.开口桥梁断面颤振及气动措施的数值与试验研究[J].同济大学学报（自然科学版），2017，45（4）：466-471.

ZHAN Q L，ZHOU Z Y，GE Y J. Numerical and experimental study of the mechanism of torsional flutter for pen-cross-section composite beams[J]. Journal of Tongji University （Natural Sci? ence），2017，45（4）：466-471.（In Chinese）

[18]杨詠昕，周锐，葛耀君.大跨度桥梁实用颤振控制方法[J].同济大学学报（自然科学版），2014，42（7）：989-997.

YANG Y X，ZHOU R，GE Y J. Practical flutter control method for long-span bridges[J]. Journal of Tongji University （Natural Science），2014，42（7）：989-997.（In Chinese）

[19]华旭刚，陈政清.宜昌庙嘴长江大桥抗风性能研究总研究报告[ R].长沙：湖南大学风工程试验研究中心，2013：18-47.

HUA X G，CHEN Z Q. Study on wind-resistance of Miaozui Yang? tze river Bridge in Yichang City[ R]. Changsha：Wind Engineer? ing Research Center，Hunan University，2013：18-47.（In Chi? nese）

[20]公路桥梁抗风设计规范：JTG/T 3360-01—2019[ S].北京：人民交通出版社，2019：66-74.

Wind-resistant design specification for highway bridges：JTG/T 3360-01—2019[ S].  Beijing：China Communications Press，2019：66-74.（In Chinese）

[21]刘小兵，陈政清，刘志文.桥梁断面颤振稳定性的直接计算法[J].振动与冲击，2013，32（1）：78-82.

LIU X B，CHEN Z Q，LIU Z W. Direct computation method for flutter stability of a bridge deck [J]. Journal of Vibration and Shock，2013，32（1）：78-82.（In Chinese）

[22]刘志文，谢普仁，陈政清，等.大跨度流线型箱梁悬索桥颤振稳定性气动优化[J].湖南大学学报（自然科学版），2019，46（3）：1-9.

LIU Z W，XIE P R，CHEN Z Q，et al. Aerodynamic optimization of flutter stability for a long-span streamlined box girder suspen ? sion bridge[J]. Journal of Hunan University （Natural Sciences），2019，46（3）：1-9.（In Chinese）