连点成线，渗透函数思想

顾文亚 许志君

在正比例教学中渗透函数思想，能有效衔接中小学教学内容，为学生学习函数图像埋下伏笔。“正比例图像”是苏教版数学教材六年级下册的教学内容，本节课主要通过正比例图像的教学，立足生长点，关注细节点，发展延伸点，加深学生对正比例关系中数值变化规律的认识，初步渗透函数思想。

一、复习旧知，锚定起点

师：上节课我们通过研究表格里两种相关联量的数据变化，认识了正比例。谁来具体说说图1中的表格所呈现的路程和时间为什么成正比例关系？

生：因为路程和时间是两种相关联的量，时间变化，路程也随着变化。通过计算，路程和相对应时间的比值一定，也就是速度总是一定。所以表中汽车行驶的路程和时间成正比例关系。

师：谁还记得正比例关系可以用怎样的式子表示？

生：y/x=k（一定）。

师：像图1这样的正比例关系，不仅可以用式子表示，还可以用图像来表示。今天我们一起来学习正比例图像。

【评析】正比例的学习，是学生第一次正式接触“变量”关系，是函数思想在小学阶段的初步渗透。本环节的复习，应用正比例的意义判断两种量是不是成正比例，为正比例图像的认识、理解与绘制做铺垫。

二、化静为动，理解图像

师：我们将表格里的时间栏画成横轴，横轴上一格表示多少小时？（课件演示：从0开始，把横轴向右拉动，动态出示刻度线和相应的数据，如图2所示）

生：横轴上的一格表示1小时。

师：随着时间的变化，路程也随着变化。这里的纵轴表示路程，纵轴上一格表示多少千米？

（课件演示：把纵轴向上拉动，动态出示刻度线和相应的数据，如图2所示）

生：纵轴上的一格表示80千米。

师：横轴和纵轴就表示表中两种相关联的量。

师：如果要用1个点表示1小时行驶80千米。这个点在哪里？你们是怎么找的？

师：如果要用1个点表示2小时行驶160千米呢？5小时呢？

（学生在作业纸上找一找）

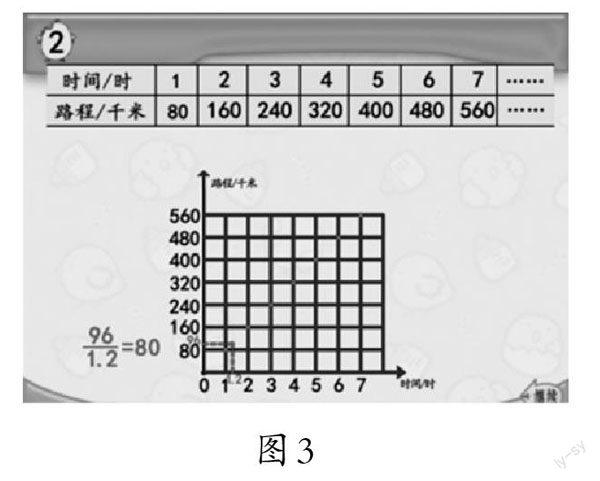
师（指着图3中的一个点）：老师在这张图上也找了一个点，这个点表示什么意思？

生：这个点横轴指向7，纵轴指向560，表示7小时行驶了560千米。

师：是的，我们用一个点就能表示这辆汽车行驶某段时间所对应的路程。你们还能找到像这样的点吗？

（学生同桌交流）

师（指着图3中的点）：其实像这样的点还有很多，比如，这个点，表示汽车1.2小时行驶96千米;这个点，表示汽车1.5小时行驶120千米;这个点，表示汽车4.3小时行驶344千米;这个点，表示汽车4.7小时行驶376千米……

师：把这些点连起来，你们有什么发现？

生：我发现这些点连起来是一条直线。

生：这些点连起来是一条线段。

师：对，这些点都在一条直线上，这条直线可以向两端延长。瞧，这个“0”点，表示汽车处于什么状态？

生：汽车还没有启动，处于静止状态。

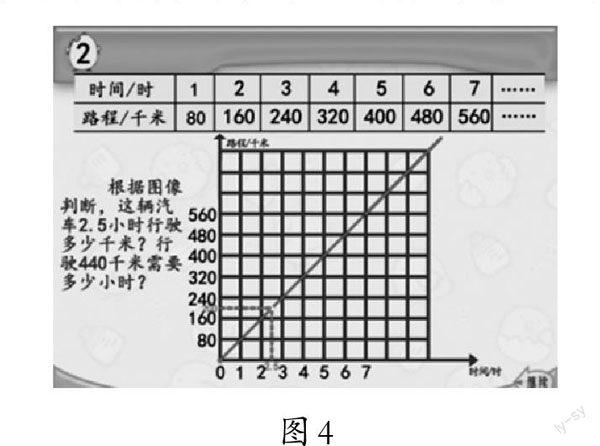
师：是的，这条直线上的每一个点都可以表示一组对应的量。瞧，汽车以同样的速度继续行驶，路程就随着时间的变化而变化。这条直线上的每个点都可以看出汽车行驶的时间和所对应的路程，这个图像就表示了时间和路程的正比例关系（如图4）。

师：根据图4中的图像，你们知道这辆汽车2.5小时行驶多少千米？行驶440千米需要多少小时？你们是怎么知道的？

生：我用直尺画两条虚线，就可以看出这辆汽车2.5小时行驶了200千米。

生：我用三角尺比一比，一条直角边指向横轴上的2.5，三角尺直角的顶点和这条直线相交，然后再看另一条直角边指向几就可以知道2.5小时行驶了200千米。

师：是个好办法。根据已知数值2.5，找到图像上对应的点，再顺着这个点找到相对应的路程。

师：行驶440千米需要多少小时呢？

生：我用三角尺比一比，根据已知数值440，找到图像上对应的点，再顺着这个点找到相对应的时间。440千米需要5.5小时。

师：同学们巧用学具，根据图像找到了相应的数据。接下来，请大家算一算路程和时间的比值是多少。

生：200÷2.5=80，比值是80。

生：400÷5=80，比值是80。

生：我觉得不管选哪个点，只要是在这条直线上，路程和时间的比值都是80。

师：在计算、观察中同学们又有了新的发现和理解，这辆汽车行驶过程中随着时间的变化，路程也随之变化，但是速度不变。看着图4，我们还可以找到、联想到更多这样的点。所以，正比例图像一般是从0开始画一条射线。

师：点（4，160）在这条直线上吗？为什么？

生：我从图上看出，这个点不在这条直线上。

生：这辆汽车每小时行驶80千米，4小时应该行驶320千米，所以这个点不在这条直线上。

生：我也是這样计算的，如果用160除以4，速度只有40，所以这个点不在这条直线上。

师：看来，利用正比例图像，可以帮助我们解决实际问题。

【评析】这一环节的教学既要让学生“看到”这些点在一条直线上，同时让学生通过“算一算”，感受这些数值是特殊的，并通过反例“点（4，160）为什么不在这条直线上”的追问，明确只有当路程和时间的比值是80时，所对应的点才在这条直线上。在画图的过程中，清楚地感受到这条直线所包含的无数个点的共同特征，感知符合不变规律的“每组数”的无限性，即体会直线背后所蕴含的知识内核。

三、生活运用，感受价值

师：第1题（如图5），请同学们自己做一做。

生：根据图像是一条直线，可以知道小玲打字的数量和时间成正比例。

生：我用三角尺帮助看图，根据省略号所绘制的图像可以看出，小玲5分钟可以打250个字，打750个字要超过14分钟。

师：同学们学会了根据图像分析、解决问题，再仔细观察，图6中这两个图像有什么相同的地方？

生：两种量都表示正比例关系，所呈现的图像都是一条射线。

生：每个点所表示的对应量的比值是一定的。

师：对，正比例关系的图像就是像这样的一条直线。上节课我们通过计算比值是否一定来判断两种量是否成正比例，现在我们还可以根据这样的图像直接判断。

师：接下来，你们会根据图7中的图像直接判断吗？

生：图7中的图像是一条射线，所以路程和时间成正比例。

生：用三角尺比画，从图上可以看出，20分钟所行的路程在4千米到8千米之间，更接近4千米，我估计比5千米多一些。

生：行10千米，10正好在8和12的中间，所以，我的三角尺这样摆，顺着另一条直角边看下来，在30分和40分之间，我估计要行35分钟。

师：同学们会使用工具，而且也做出了比较精准的比照和预估，真不错。接下来根据这里的数据，你们能画出图像吗？请同学们自己动手画一画。

【评析】在练习环节，教师安排了三个层次的练习。第1题，以形变数，根据图像直接判断两种量之间的关系;第2题，以数化形，根据表格中的数据画图，理解关系，拓展优化画图方法，进一步凸显图像的本质，渗透函数思想;第3题，形数互变，让学生在解决问题的过程中感受图像的价值，更直观、更清楚，有助于学生分析与推理问题，渗透函数思想。

四、归纳整理，拓展延伸

师：今天我们认识了正比例图像，谁来说说你的收获？

师：如果横轴上的量用x表示，纵轴上的量用y表示，在这样的图像上，可以找到任意一个x所对应的y。同学们，随着以后的学习，这条直线还可以向其他方向延伸，你们觉得会形成怎样的图像呢？课后大家可以继续研究。

【评析】正比例图像是一种特殊的一次函数图像，函数图像既是一个重要的数学概念，又是研究函数的重要工具，对培养学生的函数观念和数形结合思想具有重要作用。

【总析】

1.立足生长点，让正比例关系“看得见”。在正比例图像的形成过程中，“一个点能表示这辆汽车行驶某段时间及相应路程这样一组对应的数值”，这是学生上节课学习的内容，在此基础上教师提问“你们还能找到像这样的点吗”？预估学生找到的都是格点上的点，及时补充“其实像这样的点还有很多”，随机出示格点之间的点，不断增加点的密度，让学生初步感受这些点可能在一条直线上，清晰地看见这条直线上有很多个这样的点，从而感受正比例图像的连续性，渗透函数的连续性。

2.关注细节点，让正比例关系“看得清”。正比例图像是用一条直线把一些特殊的点连接起来。在连点成线的过程中，学生最容易忽视两点：一是对图像起点的认识，二是对图像终点的认识。因此，本节课教学从“横轴和纵轴的出示”“各点位置的确定”到“图像的形成”，都以动态呈现。化靜为动，在教学中关注横轴与纵轴所表示的意思，关注点的位置的确定过程，在逐步呈现的过程中帮助学生经历图像的形成过程，促进学生对点所表示意思的理解，渗透函数思想。

3.发展延伸点，让正比例关系“看得远”。本节课教学从例题到习题的设计，数形结合，动态呈现。连点成线是绘制正比例图像的方法和步骤，体现了正比例图像的工具性。从有数个点走向无数个点，体现了正比例图像的意义。

（作者单位：江苏省无锡市张泾实验小学 ）