以生为本，数形结合领悟深层算理

杨雪芬

[摘要] 在人教版小学数学三年级下册“两位数乘两位数（不进位）”一课的教学中，教师可以通过课前的调查与分析，把握学生的学习起点，找到教学的重点难点，如消除学生对点子图的陌生感及有效运用点子图帮助学生理解算理。在教学的过程中，教师则需要以生为本，通过回顾旧知、用图形探究数学规律、利用数形结合找到数学算理等策略，帮助学生转新为旧、循理入法、以理取法，从而提高学生的数学思维能力。

[关键词] 两位数乘两位数;数形结合;乘法运算;小学数学教学

一、课前思考

数与形是数学学科中两个常见的研究对象，借助一定的手段，可以使数与形之间相互转化。数形结合将直观的图形与抽象的数学语言相结合，把数学问题转化为学生已有的知识经验，以促进新旧知识间的关联与转化，使复杂问题简单化、抽象问题具体化，从而实现知识建构与问题解决。“两位数乘两位数（不进位）”这节课是人教版教材三年级下册课本中的内容，在這之前，学生已经学习了两位数乘一位数的笔算及两位数乘一位数、两位数乘整十整百数的口算。对于三年级学生来说，学习两位数乘两位数的笔算是一次较大的飞跃，因为这一单元是小学阶段四则运算的重要内容之一，不仅是本单元的重点，同时也是今后学生学习三位数乘两位数及小数乘法的必备基础知识。因此，如何运用数形结合理解两位数乘两位数的算理是这节课的重点，也是难点。但在之前的教学实践中发现，学生难以把竖式和点子图中的四部分很好地联系起来，更不用说真正运用数形结合思想来理解竖式中的每一步算理。为了引导学生联结先备知识，辅以图形表征进行沟通，达到理解算理、突破难点的教学目标，我们课题组进行了课前的分析与调查。

其一，学生在此之前学习笔算的经历大多是借助摆小棒来理解算理，且在这个单元的口算学习中也是通过摆小正方体或实物图的方式来帮助理解。而在本节课中，教材安排了借助点子图的方式帮助学生理解算理、探究算法，进而得到乘法算式的过程。点子图相较于摆小棒和实物图要更加抽象，对学生的思维能力要求更高。虽然对于点子图而言，学生以前也接触过，但并不熟悉，所以理解起来会有一定的困难。

其二，为了解学生是否会计算两位数乘两位数（不进位）的乘法，教师让一个班级的学生（37人）在学习本节课前进行了课前小测，以检测学生对两位数乘两位数（不进位）的算理、算法、竖式计算的掌握情况。

通过前测，教师了解到，学生中有19人能正确写出测试题中23×13的笔算过程，占总人数的51.35%。其中，考查算理的一题只有4个学生会填，这说明在上课前有相当一部分学生已经通过各种方式掌握了笔算两位数乘两位数的方法，但大部分学生对两位数乘两位数的算理知其然而不知所以然。

通过对教材和学生知识起点的分析，教师发现，学生第一次接触需要乘两次的情况，部分学生对算法也有一定认识，但对算理并不理解。另外，学生对点子图也不熟悉，对把点子图分成四部分以理解笔算的过程难以接受，教学不容易达到通过数形结合使学生变模糊接受为清晰理解的效果。因此，本节课需要重点研究如何解决以下两个问题：（1）如何消除学生对点子图的陌生感;（2）如何有效运用点子图帮助学生理解算理。

二、教学过程

基于上文的分析，教师做了以下处理与调整。首先，为了消除学生对点子图的陌生感，更好地利用点子图理解笔算两位数乘两位数的算理，教师在前面的“两位数乘一位数”“两位数乘整十数”口算教学中除了使用实物图外，还有意识地逐步过渡到用点子图帮助学生理解口算的算理。其次，教师对运用点子图理解笔算过程的教学过程进行了分层处理，以降低理解的难度。

【教学片段一】回顾旧知，引出新知

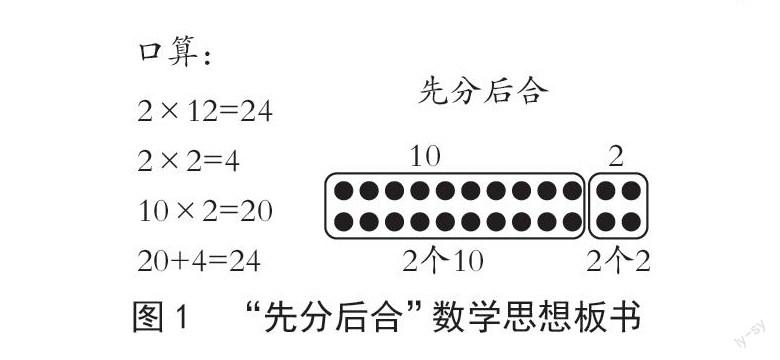
师：你会口算2×12吗？（课件出示：口算2×12）请进行口算，并与同桌说说你的口算结果和过程。

师：我们在学习这个知识的过程中借助了点子图，把12个点分成10个点和2个点，先算2个2，再算2个10，再把他们合起来，也就是先分后合（板书如图1），为什么要先分后合呢？

生：因为要把新学的知识尝试用旧知识来解决。

在教学本单元的乘法口算时，教师有意识地让学生利用点子图来理解口算过程，消除了学生对点子图的陌生感。所以，在复习铺垫环节，教师再次安排用点子图回顾“2×12”的口算过程，此复习环节很流畅，节省了重新学习点子图的时间，同时也为学生学习本节课中利用点子图理解笔算过程的新知打下了基础。

【教学片段二】用点子图探究14×12的口算

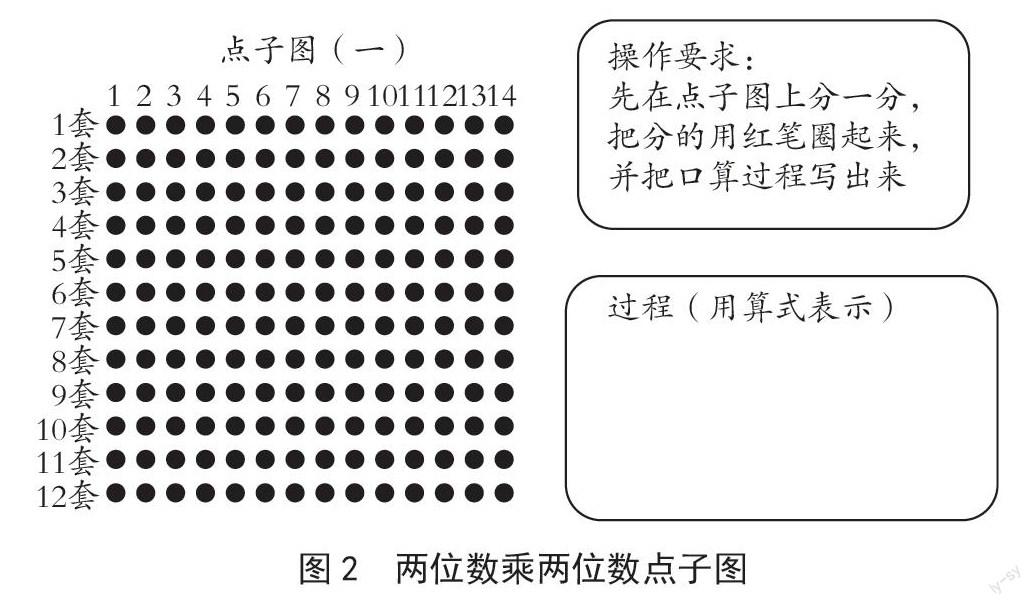
师：我们通过先分后合的方法把新知识转化成旧知识，那么我们在学习今天这些新知识时能不能也利用这些方法呢？（事先用课件把书本转化成电子图）

师：请同学们拿出学习单，找到点子图（如图2），思考：可以把12套书分成几套和几套？提示一下，为的是能转化成我们已学过的知识哦。

师：哪个同学能拿着你的学习单上来展示一下想法？

生1：先把12套分成6套和6套，再用14×6=84（本），2个84，84+84=168（本）。

生2：我是先把12套分成10套和2套，10×14=

140（本），2×14=28（本），再把两份合起来。

师：还有其他想法吗？老师收集了一些同学的方法，我们一起来看看。第一种方法把12套分成了10套和2套，第二种方法把12套分成6×2套，第三种方法把12套分成3×4套，第四种方法把12套分成4套和8套。这些方法五花八门，但他们的方法都用到了先分后合，那这样分的目的是什么？

生：要达到口算的目的。

师：这也是把新知识转化成旧知识。这些都是口算的方法，那两位数乘两位数能不能笔算呢？（板书课题）

教学过程中教师提供给学生直观的点子图作为研究素材，让学生尝试利用已有的知识解决新问题，并要求学生用点子图把自己的方法表示出来，这是让学生经历用图示表征并解释算法的过程。在复习环节中强调运用“先分后合”把新知转化成旧知的数学思想，这为接下来学生尝试解决本节课新知计算“14×12”提供了思考方向。所以，当学生遇到“14×12”这种两位数乘两位数的新问题时，就能自然而然地联想到运用这种方法来解决。解决数学问题的方法虽然有很多种，且这些方法还都不完全相同，但归根结底，它们实际上都是运用了“先分后合”“新旧知识转化”的数学思想。

【教学片段三】数图结合，理解计算方法背后的算理

师：两位数乘两位数该怎样笔算呢？可以继续借助点子图帮我们想一想怎样笔算。笔算列竖式和一位数那会儿是一样的，相同数位对齐。例如，在笔算14×12时，你认为应该先算什么，再算什么？和同桌讨论一下。

生1：我认为应该先算个位即14×2，再算14×10。

生2：我认为应该先算2×14，再算10×14。

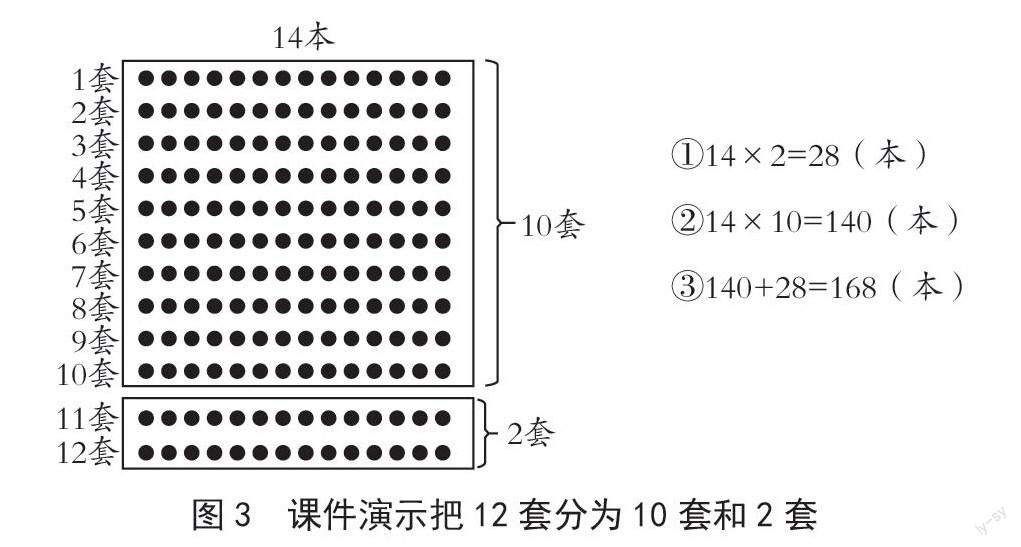
师：大家都是把12分成了10和2，先算14×2。现在请同学们拿出点子图，像老师这样分一分，把 12 套分成10套和2套，再用算式表示出来。（课件演示把12套分为10套和2套，如图3）

通过课件和让学生再分一分、圈一圈，直观而完整地呈现出把图中12套分成10套和2套的过程，并对应是哪个算式。基于此，学生对点子图与算式的联系就能建立起来，而不是分开而独立地理解。

师：这是我们的口算过程，那现在同学们尝试着用竖式把口算過程记录下来。注意，竖式的记录要体现第一步算2套的，第二步算10套的，第三步再合并起来（过程略）。

师：我们来分析一下这位同学写的竖式是否体现了我们刚刚的口算过程。比如，28是怎么来的？

生：14×2，也就是2套书的。

师：那140又是怎么得来的，是图中的哪一部分？

师：第一步先算2套书的本数，第二步算10套书的本数，第三步把两部分合并起来。也就是说这两道竖式都对了。

师：下面我们再来仔细看下每一步算的是什么。第一步算2套的，14×2，大家还记得14×2 是怎么算的？

生：以前学过，是把14分成10和4，先算4×2=8，

再算10×2=20，最后算8+20=28。

师：先算4×2=8，是图里的哪一部分？再算 10×2=20，又指的是图里的哪一部分？

师：再算10套书的，也就是14×10，14×10我们又是把什么分成的？

生：把14分成10和4。

师：先算10套，每套4本书的总本数，也就4×10，谁来指一下？4个10是40，4写在十位，个位这个“0”是否可以不写？为什么？

生：可以不写，应该4写在十位上表示40。

师：再算10套10本的，10个10本是多少？所以百位写“1”，再把两部分合起来，8+0=8，2+4=6，把“1”拉下来，所以14×12=168（本）。现在同学们明白笔算怎么算了吗？请大家一起来说一说笔算过程。

在过往的教学实践中教师发现，如果一口气把点子图划分成四部分来理解算理，学生学起来相当吃力，且多数学生吸收不了。所以，这节课我们进行了分层处理，利用点子图与数形结合思想来帮助学生理解算

理。即：

第一，引导学生计算12套书总本数。教师先把12套书分成10套和2套，再引导学生通过点子图分一分，为的是理解在计算两位数乘两位数时，可以通过先分后合的方法转化成两位数乘一位数和两位数乘整十数，也就是把 14×12分成14×2和14×10，最后把两次的乘积加起来。由于有前面“2×12”口算过程的铺垫，学生理解这一层不难。接着，教师可以引导学生利用竖式来记录口算过程，提示竖式要体现口算的三步。这样，学生就可以初步把竖式计算过程同口算过程、点子图紧密联系起来，再通过图形表征、算式表征与计算方法之间的联系来理解14×12的结果。

第二，利用前面点子图与口算过程的关系，可以实现把点子图和14×2 的笔算过程联系起来以理解算理。具体为，把2套点子图再分成两份，就是把14本分成10本和4本，也就是用2分别与4和10相乘。在教学这部分时，图中的10套虚化处理，为的是突出2套，竖式中12的1也遮挡住，这样也就是与口算的算理及计算过程一致，学生就很容易理解。同时，在教学“14×10”时也一样，两层的处理都需要教师紧密联系口算、点子图与计算过程之间的关系，化新为旧，让学生在操作中从“形”的方面进行具体思考，并渐渐过渡到对“数”的理解，再上升为理解算理的层次。最后，教师需要在点子图中寻找竖式计算的足迹，帮助学生还原最简单、最直观的道理和方法，使算法和算理有机地融为一体。

三、思考与启示

数形结合是小学数学教与学中的一种重要的思想与方法，通过数与形的相互转化及配合来解决数学问题，往往能达到把复杂问题简单化、抽象问题形象化的效果。在数学教学中，教师应当根据学生实际，以学生为本，充分利用这种思想进行课程教学的改进与优化。

第一，关注学生已有的知识经验、促进新旧知识间的关联、把握好学生的学习起点是设计适合学生自主学习的教学过程的基本立足点。教师通过了解学生已有的知识经验，充分利用已有知识为学习新的知识而服务，化新为旧，有效培养学生的数学思维能力。

第二，教师应以生为本，适时调整教学策略。计算教学不仅是要教给学生计算方法，更重要的是要引导学生掌握算理并提升学生的数学思维能力。在小学数学教学的过程中，小学生的思维能力处于从直观到抽象发展的阶段。三年级学生在数学学习的过程中，需要借助较多的动手操作实践和直观表象展示作为支撑。利用数形结合的方法，教师可以有效地将“冰冷”的算法和“神秘”的算理进行深层次融合，启发学生“循理入法，以理取法”，通过道理的引领让法则的建立有根基，通过算理的支持让枯燥的算法丰润起来。例如，教师可以通过借助直观手段（如点子图）与算式相对应，产生数形结合，引导学生亲历建构两位数乘两位数数学模型这一过程。而这个过程必须以生为本，教师除了要全盘考虑知识体系外，还要站在学生的思维角度去思考问题，从学生的实际水平出发，正确把握好教学内容的难易程度，并根据学生的知识水平进行教学策略调整，引领学生厘清数形之间的一一对应关系，以此把握数学问题中的诸多内隐道理与方法，从而达到化难为易和化繁为简的目的。

总之，在计算教学中，教师应该以学生为中心，以最大限度地提高学生的数学思维能力为重，在此基础上打造数形结合的高效数学课堂。

[参考文献]

[1]褚金花.在“形”“数”互变中提高小学生的数学思维能力[J].学周刊，2020（09）：85-86.

[2]方梅珠.基于数形结合理念优化数学学习的教学策略[J].新课程研究（上旬刊），2018（07）：71-72.

[3]陈月初.回归真实“需求”，“点”亮直观建模——以《两位数乘两位数笔算乘法（不进位）》为例[J].山西教育（教学），2021（07）：45-46.