小学数学结构化教学探析
2022-05-30郭葛晨晨
郭葛晨晨
[摘 要] 小学数学结构化教学中,教师应重视结构关联,要求学生不仅要关注数学知识点的结构关联,更要从数学思维和认知层面深入结构关联,从而促进学生深度学习,实现学生核心素养的关联生长。
[关键词] 小学数学;结构化教学;运算定律
随着现代教学实践中工具的使用越来越频繁,学生在学习过程中的信息获取也越来越碎片化。随之影响的是学生的思维习惯和认知深度,学生的思维和认知缺乏整体性和关联性,难以搭建起统一的结构主体。小学数学结构化学习是指基于数学知识,将数学知识结构化,形成知识体系,帮助学生深刻理解数学知识和发展数学思维。基于此,開展小学数学结构化教学,不仅要求教师关注数学知识的结构关联,还要从学生认知和思维层面深入探究实践思路。通过不断探索、有效整合、及时反思,帮助学生经历认知形成和思维重塑的过程,从而建构起学习数学知识的基本思路,为后续的数学深度学习打下坚实基础。
一、探析数学知识点的结构关联
要如何理解“帮助学生搭建知识点的结构关联,有助于学生深刻理解知识,并灵活运用知识”这一结论呢?我们可以从美国著名认知心理学家布鲁纳说过的一句话中找到答案,即“掌握事物的结构,就是以使许多别的东西与它有意义地联系起来的方式去理解它”。具体来说,要想完成小学数学的结构化教学,我们必须从数学知识点出发,通过探究数学知识的结构关联,帮助学生搭建数学知识的完整框架。要想抓住数学知识的本质,我们可以依据教材,从课时内容的各个关键环节出发,探究它们之间的关联性,再分析课时内容与同单元其他章节内容、同板块其他单元内容、同学科其他板块内容之间的关联性,帮助学生从内到外深度理解知识,从外到内循环高效发展思维。
1. 关联分析课时内容的关键部分
从数学知识的本质出发,通过分析课时内容的关键部分完成对知识的分析和建构,从而不断优化教学内容和呈现思路,丰富教学品质,提升教学质量。
【案例】 以“运算定律”这一章节的教学为例,我们可以将这部分内容,拆解成加法定律和乘法定律这两个大的课时,进而分解为加法交换律、加法结合律、加法运算定律的应用、简便运算,乘法交换律、乘法结合律、乘法分配律,复杂问题的多样运算。通过对这些关键知识再排列和再认知,实现数学学习的再创造,从而不断提升学习效果和教学品质。
2. 关联分析课时内容与同单元其他章节内容
课时内容并不是单一孤立存在的,它们是有联系的,相互的联系构成了一个有机整体。因此,教师在完成对课时内容的讲授后,要关注同单元其他章节内容与本课时内容的联系,帮助学生认识课时内容与其他章节内容之间的结构关联,发现它们之间的内在联系,做好互相渗透、衔接、过渡,从而完善学生的认知结构。
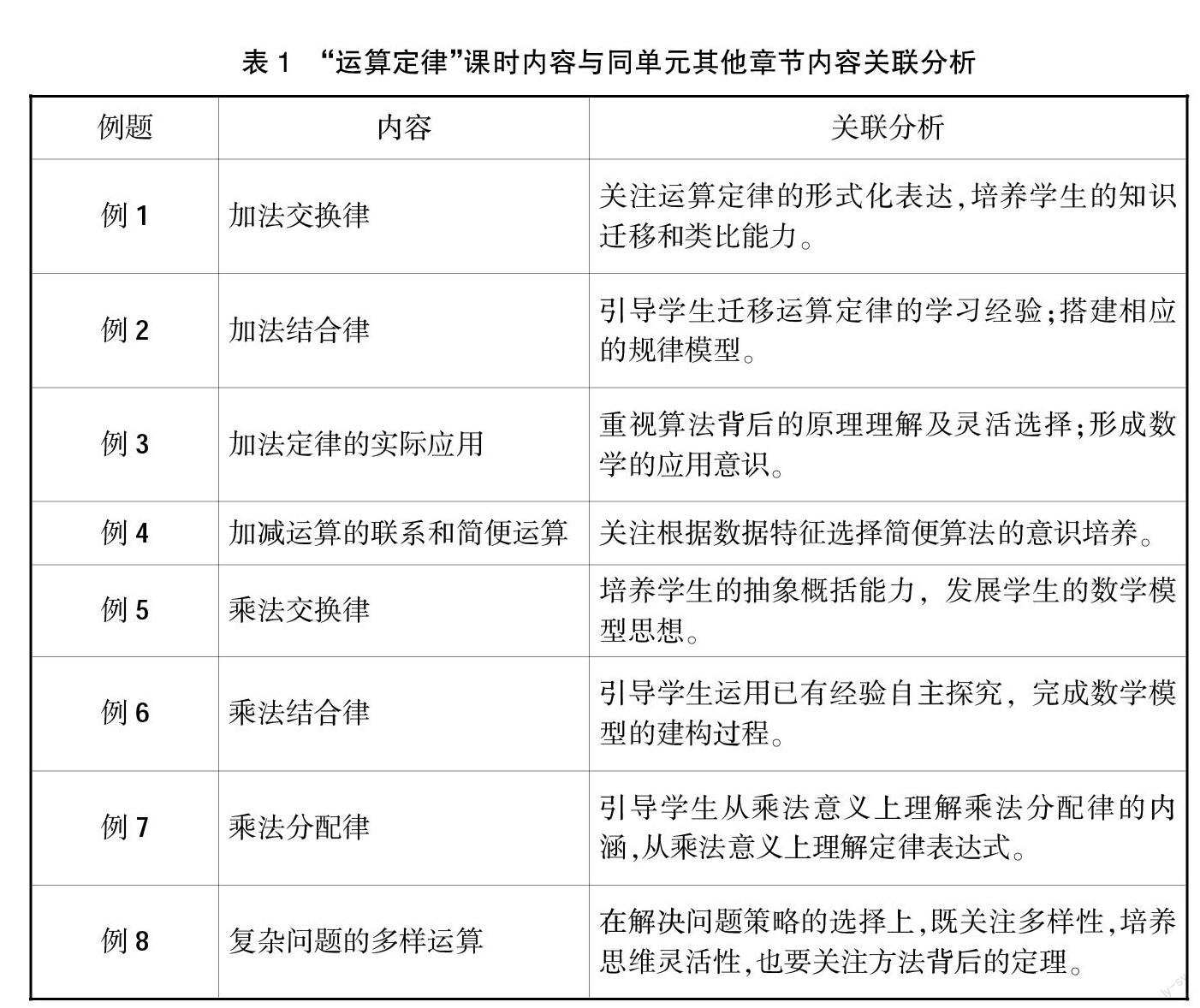
【案例】 以“运算定律”这一章节的教学为例,我们基于教材例题对本章节课时内容与同单元其他章节内容进行对比分析,如表1所示。
从表1中我们可以看出,本课时内容“运算定律”是整个单元的重点,在章节学习中起着重要作用。在这一课时中,学生必须直观并且深刻地了解和认识加法与乘法的运算定律,并将它们延伸至减法和除法,学生需要学会计算复杂问题,并能应用定律解决实际问题。
3. 关联分析课时内容与相关单元内容
如果将课时内容比作一个点,那么单元内容是一条线,相关单元内容即是一个面,由点及线,由线到面,形成知识体系。因此,教师在实际教学活动中,要充分认识课时内容在相关单元内容中的重要性,明确板块教学的要求,努力构建点线面全面覆盖的整体认知结构。
【案例】以“运算定律”这一内容为例,这一课时内容是四则运算的重点,教师除了要联系之前教学实践中总结的经验和规律,帮助学生理解加法或乘法交换律(交换两个加数或因数的位置,不改变计算结果),还要联系后续的小数加减法和乘除法混合运算,帮助学生搭建起有关实数的四则运算的整体知识框架。
二、探析数学认知的结构关联
数学知识是学生在解决数学问题的过程中获得并内化的。在这个过程中,学生依序建构活动程序和对象,最终组织概括成可以理解问题、解决问题的整体架构。学生的数学学习一般要经历以下四个认知阶段:
1. 活动阶段
活动包括具体的外在的动作,例如实验、操作、游戏等,还包括内在的思维活动,如回忆、对比、猜想等。它是帮助学生一步步加深对数学对象的认识印象的有效途径。在实际的教学实践中,教师应当给予符合学生思维的问题情境,引导学生通过相应的活动初步感知数学对象。
2. 程序阶段
当活动经过多次重复而被学生熟悉和认识后,就可以内化为一种被称为程序的心理反应。学生具备这种程序后,就能在头脑中自动化运行而不需要具体操作。经过多次重复的反思后,学生可以逐步剔除数学对象的非本质属性,从而认识数学对象的本质属性。
3. 对象阶段
当学生能将程序作为一个整体进行独立操作和概括总结时,这个程序就变成了一种心理对象,可以帮助学生实现从感性认识到理性认识的飞跃,从而发生质变。通过活动和程序认识,学生可以抽象概括出数学对象的本质属性,从而将其变得形式化或符号化,成为一个可以参与到结构关联中的独立个体。这样学生就可以将其作为一个数学认知带入新的数学活动中,提升数学活动的思维层次,如此往复,学生的数学认知水平将会不断提高。
4. 图式阶段
当学生对活动程序和对象进行有机整合并形成初步的认知结构时,图示应运而生。这个阶段是学生认知的结构化阶段,通过图示可实现数学学习关联结构化。当然,学生的初步图示不可能尽善尽美,还需要在后续的学习和解题实践中不断修正与完善,因此教师在后续的数学教学过程中,要引导学生不断更新和反思认知结构,帮助学生丰富图示的内涵和本质。在具体教学实践中,教师可以通过思维导图、韦恩图、知识结构框架图等让学生学会梳理数学知识,帮助学生总结归纳数学知识,提升学生的建构能力和认知水平。
三、探析数学思维的结构关联
数学思维是数学认知的核心,构建认知结构的目的就是帮助学生发展数学思维,提高解题的灵活性。在小学数学结构化学习过程中,学生的思维发展主要有直观思维、程序思维、抽象思维和形式思维等阶段。教师在实际教学活动中要把握住学生思维发展和认知发展是一一对应的。也就是说,随着学生知识结构的逐步完善,数学认知水平的不断深入,其数学思维也会不断成长,因此,只要做好学生知识点的结构关联和认知水平的基础搭建,学生的数学思维能力就一定会有较大提升。
当然,小学数学的结构化教学,并不仅仅局限于数学知识点的结构关联、数学认知的结构关联和数学思维的结构关联,还包括数学情感和价值观的建立、数学方法的学习。鉴于文章篇幅有限,这里就不一一详述,大家可以根据实际教学经验自行探究分析。
