“微元法”在高中物理解题中的应用探索

张立强

摘要：高中物理的解题教学中，教师需遵循教育的发展要求，注重教育思想的创新，将微元法运用于高中物理的解题教学中，以此使学生更快发现物理题中物理规律的同时，促进学生的解题效率提高.基于此，本文主要对微元法进行阐述，并提出微元法在高中物理解题中的应用策略.

关键词：高中物理;解题;微元法;应用;策略

中图分类号：G632文献标识码：A文章编号：1008-0333（2022）21-0073-03

微元法作为高中物理问题解决的基本思路与方法，将其运用于高中物理的知识体系学习与问题解决中，可通过设定不同的有限元对题干当中的各种量进行表示，并经过将不同量转变成相同量，对题干问题进行有效分析，从而实现复杂物理问题的简单化.在高中物理的解题教学中运用微元法，将物理知识与概念以教学的形式进行表现，并依据教学方式加以处理，不仅能实现解题准确率以及效率的提高，而且还能促进学生的物理成绩提高，从而使学生充分掌握微元法的理论知识与应用技巧的同时，实现物理题的解题实效性提高.

1微元法的概述

所谓微元法，其是分析与解决相关物理问题常用的方法，也是部分至整体的一种思维方法.将微元法运用于较为繁琐的物理试题中，不仅能实现物理题的简便化，而且还能使学生更快的获得正确答案.微元法在具体应用中，其本质就是对问题实施分解，呈现出“元过程”，依据某物理规律，对问题进行研究分解，然后对物理思想和物理方法实施加工与处理，以实现物理问题的有效解决.依据微元法进行物理问题的解决步骤具体为：第一，对需解决的问题进行研究，依据物理题的条件，对微元对象进行明确;第二，将分解后的微元对象与物理模型有效结合，根据物理方式对物理题目的对象进行求解，这对于较为繁琐的物理问题的解决中，通常具有事半功倍的效果;第三，将解题的结构推广至各微元体系当中，通过微元关联引入相关物理方法，并对物理问题进行逐步处理，从而获得正确的答案.将微元法运用于高中物理的解题，则能使原先较为复杂化的物理问题化解成简单问题，从而使学生的解题难度得以降低的同时，实现解题效率的提高.

2高中物理运用“微元法”解题的过程2.1用“微元法”解题，增加解题思路

高中物理的解题中运用微元法，其不仅能够使学生多了一种解题的思路，而且还有助于学生的思维发散.将微元法促进匀加速运动的时间与位移的表达式作为案例，假设物体运动初速度是v其加速度是a，呈匀加速直线运动，通过一段的时间t后，求解物体的时间与位移之间的关系表达式.首先，需根据题意开展微元法首步，即取元，把物体运动的路程分解成不同的小路径，由于在较短的路程中，物体运动时间通常也是极短的，因此，需将物体当做成在小路程中进行匀速直线的运动，以此得出物体处于极短时间中走出的路程具体表示式.然后，对整体路程表达式进行求解，绘制出物体的运动图像，将x轴作为时间t，将y轴作为物体运动的速度v，以求解面积的方式，计算出物体的时间与位移的表达式.

2.2用“微元法”解题，明晰解题过程

将微元法运用于物理解题中，学生只需要依据微元法的实际解题步骤进行逐步计算，就能实现迅速解题，并形成了非常明晰的解题过程.将半径作为R的圆的四分之一平放于光滑水平面上，通过光滑球面，在上面放置个光滑且均匀的钢链，将钢链的一侧固定于光滑的曲面顶点上，此时，钢链另一侧正好不接触桌面，且钢链的密度都是a，求解出钢链顶端所承受的拉力F，由于无法将钢链当做是一个质点实施分析，且每节钢链对于端点的实际拉力却有都不同，因此，依据传统化解题方式是无法有效解决该物理问题的.而通过微元法进行物理问题解决时，首先，需明确分析的对象是钢链，通过微元法进行取元，对钢链上的极小段实施分析，依据受力平衡，求解出小段钢链对于顶端拉力的数值;其次，依据对应的几何关系实施求和，以求解出顶端的拉力值.通过微元法进行物理问题的解决，不仅能够使解题的步骤更加简单，而且还能依据物理题的条件与对应的几何关系，实现物理问题的有效解决.

2.3用“微元法”解题，促进提升题解决物理问题一般是不能把全部的研究对象当做是整体或者一个质点，其中任何部分承受到的力都是有所不同的，学生通常是按照传统的分类讨论的方法对物理问题进行解答.如一条质地相对均匀的绳子，其绳长是a，质量是m，把绳子的一侧固定于一块木板的钉子上，绳子另一侧则由钉子的位置掉落，求取绳子另一侧与钉子的距离是x的时候，钉子对于绳子的作用力为多少？本题主要就是对学生应用“微元法”的能力进行考查，学生需依据微元法的有关步骤加实施解答，可经过建造模型、取元、求和的步骤，进行物理问题的解答，以顺利的得出问题答案.因此，面对些无法解答的物理题，则能通过微元法的运用实现顺利求解.

3“微元法”在高中物理解题中的应用策略

3.1基于“微元法”的电磁感应题求解

电磁感应作为高中阶段物理知识中较为常见且重要的一个知识点，相关知识通常是高考物理试题中考查的重点内容，占据着极高的分值，学生只有充分掌握相关知识点，才能在对电磁感应问题解答时，形成良好的解题思路.而将微元法运用于电磁感应题的求解中，不仅能够使学生充分掌握问题的解答规律，而且还能使学生迅速解决相关类型的物理题.以某个电磁感应题为例：一个金属杆被置于完全平行以及光滑的导轨上，其装置呈现为水平状态，通过m表示质量，已知導轨的间距为L，在导轨的另一侧连接上电阻，其电阻值是R，忽略其他的电阻状况，有垂直导轨以及相对均匀磁场，磁感应强度通过字母B进行表示，请依据金属杆初速度计算出导轨朝着右侧移动所得的最大距离.

3.2基于“微元法”的运动力学求解

在对非匀速运动的力学问题进行处理时，通过一般的运动类题目的解决方法实施解题，不仅会造成运算量的增加，而且还无法解答出正确的答案.但是，通过“微元法”的运用，则能从研究对象的最小部分作为分析进行入手，促进复杂问题的简单化，以促使学生更快的解决运动力学的问题，并获取到正确答案.

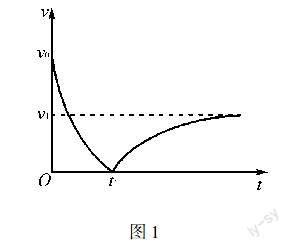
例如，地面上通过v0的速度向上进行竖直抛出某个物体，其质量为m，已知物体的空气阻力和速度是成正比的，物体实际运动的速率如图1.

请问：（1）物体由最初抛出至最终落地，空气阻力共做多少功？（2）物体被抛出来的瞬间，其加速度是多少？（3）物体位于t1时的高度是多少？

解析依据题意可知，物体运动的情形是：最初通过v0的速度逐渐向上进行减速运动，受到向下的重力以及空气阻力的作用，t1到达最高点的时候，其速率通常为0，然后再下一秒进行下落，该阶段，其受到了向上空气阻力以及向下重力的影响，在回到地面时，若物体做匀速运动，落地的速率是v1，此时，可通过“微元法”进行问题解答.

解答：（1）依据动能定理，能够得出：Wf=12mv21-12mv20，因此，空气的阻力做功是：Wf=12mv21-12mv20.

（2）由于空气的阻力是：f=kv;又因为物体在具体落地之前，做匀速运动，所以，mg=kv1;若物体在抛出时初始的加速度为a0，由此可知：ma0=mg+kv0;所以，a0=（1+v0/v1）g.

（3）假設物体上升的过程当中，其速度是v，其加速度是a，那么，-（mg+kv）=ma，即a=-g-vg/v1;通过“微元法”的运用把物体上升的过程分解成多个小过程，假设任意的微小时间Δt中，物体的速度变化是Δv，也就是Δv=aΔt=-gΔt-vΔtg/v1;又因为vΔt=Δh，所以ΣΔv=-gΣΔt-ΣΔh;根据题意可知：0-v0=-gt1-（g/v1）H;由此可解得：物体最大高度是H=v1v0/g-v1t1.

通过“微元法”进行动力学的问题解答，不仅能解决不同的复杂问题，使复杂的物理问题化繁为简，而且还能从局部的问题作为出发点，逐渐解决复杂的物理问题，从而使学生实现快速解题.

3.3基于“微元法”的位移问题求解

对于高中物理的位移问题而言，通过“微元法”进行处理，可以将位移的过程分为无数Δt进行问题简化.高中物理的具体解题中，可通过“微元法”的运用，对光滑平行轨迹上的位移问题进行解决，从而实现物理位移问题的快速解答.

例如，光滑平行的轨道上，有个金属性质的样品，其质量是m，轨道之间的距离为L，其一侧的电阻是R，其平面受到了均匀磁场的垂直作用，且磁感应的强度可以达到B，金属棒通过v0的初速度朝右侧进行水平运动，金属轨道若足够长，其最大的移动距离可到达多少？

解析通过“微元法”的思维，需对金属棒的微元实施单独分析，明确研究对象的具体运动情形，以此明确物理问题的解答思路.金属棒受合力朝左，因此，朝右进行减速运动，在微小的时段Δt中，可被认作是匀速直线的运动.

3.4基于“微元法”的做功问题求解

做功问题的求解属于高中物理解题中的常见问题，通过“微元法”的运用，就能将做功的全过程划分成多个阶段，以实现问题简化的目标.

例如，已知力F的大小不变，在圆的边缘进行做功，圆半径是R，力F顺着圆周进行做运动，其作用方向和圆周切线的方向一致.在一圈运动完成之后，回到原先的出发位置之后，力F共做多少功？

综上所述，高中物理的内容相对逻辑化且抽象化，通过“微元法”的运用，不仅能为高中物理的解题明确方向，促进学生的思维空间延伸以及物理问题的解决，而且还能通过微元法的应用，促进学生对于物理知识的内化与巩固，并深化对物理知识与技能的了解，从而使学生的解题效率得以提高的同时，促进学生的综合素养提升.

参考文献：

[1]曹志扬.微元法在高中物理解题过程中的应用分析[J].中学生数理化（高考理化），2017（9）：1.

[2]姜凯元.高中物理学习中应用微元法进行解题的实践分析[J].数理化解题研究，2018（12）：61-62.

[3]张海军，唐安全.微元法在高中物理解题中的应用探究[J].中学生理科应试，2019（8）：3.

[4]乔永.微元法在高中物理解题中的应用探讨[J].试题与研究：教学论坛，2019（4）：78.

[5]王鹏.微元法在高中物理解题中的运用实践研究[J].知识文库，2017（14）：152-153.

[责任编辑：李璟]