初中数学课堂教学中建模思想的渗透
2022-05-30林凯国
林凯国

用数学方法构建数学模型解决问题的素养,是数学学科的核心素养之一。将数学建模作为核心素养并融入课程内容中是课程改革的一项重要举措,能够有效地改变教师教学方式和学生学习方式,为数学联系现实世界提供了一种有效方式。
一、初中数学渗透建模思想的意义
初中数学渗透建模思想的意义主要体现在两个方面,一是数学建模培养了学生的抽象能力。构建数学模型,从问题所包含的诸多要素中选择建构某个数学概念或规律所需的要素,再对这些要素之间的关系进行综合分析,将这些关系用数学的语言和方法,通过抽象、简化的手段描述出来。二是建立数学模型解决问题就是让学生对已学的知识进行合理应用,有利于学生应用能力的提升。事实上,数学源自生产实践,与现实生活密切相关,几乎所有科学领域都要用到数学知识。用数学思想方法解决现实问题,更加简约、便捷和有效,数学建模的本质是用数学的思维思考世界。
二、初中阶段常用的数学模型
1.方程(组)模型。将题目条件用数学语言转化成方程,通过解方程解决实际问题。方程模型是最基本的数学模型之一,学生学会建立方程模型,就可以基于数量关系的角度对现实中貌似复杂实有规律的各种问题形成准确、清晰的认知。通常工程问题、行程问题都可以通过方程模型描述出来。
2.不等式(组)模型。从数量关系的角度分析问题,比方程模型更具有普遍性。不等式模型将题中的相关数据转化成不等式问题,用以研究这些数量之间的大小关系和变化规律,不等式模型除了需要根据题意列出相关的代数式,常常还需要对代数式的值进行适当的缩小或放大,构建不等式模型解决实际问题。常见的方案选择、市场营销问题都可以通过构建不等式模型来解决。
3.函数模型。通过函数模型学生可以更好地理解数学问题中变量的变化情况,初步预测变量的变化规律。最大(小)值问题和大多数的动态图形面积、动点运动问题、营销策略问题都可以借助函数模型解决。
4.几何模型。通过对图形、图形关系的抽象,运用几何公式、定理进行运算、推理论证,研究它们的空间形式,构建几何模型,表达现实世界的本质、关系和规律。
5.概率模型。用来描述各种事件发生的可能性的大小,包括古典概率、统计概率和图形概率三种模型,用途非常广泛。抽奖、博彩问题常用概率模型求解。
三、初中数学渗透建模思想的基本原则
教师在日常教学中渗透数学模型思想要遵循两个原则。第一个原则是要充分了解数学思想方法、学会数学思维。数学思维包括两种,一种是再现性思维,即对所学的知识进行复现,思考的结果是學生比较熟悉的或者是已知的;另一种是发现性思维,即需要针对所学知识有所创新。第二个原则要充分依托教材,重视数学活动的教学。教材是建模思想的基础,欧几里得几何学本身是对现实世界的空间形式所提出的一个数学模型。教师要结合学情对教材进行加工整理、归类,总结提炼解决问题的方法,在课堂上进行数学建模的指导,教会学生应用数学思维解决实际问题,从建模角度引导学生了解数学概念、公式的实际应用方法及数学思想背景,提高其知识应用能力。
四、初中数学课堂教学中建模思想的渗透策略
(一)培养学生的建模思想
构建数学模型是一个复杂的过程,初中教学中涉及需要建模的问题较少,学生还未产生将题目中多种不同的已知条件与要求整合起来进行分析的意识,因此教师要针对这一情况,由易到难建构数学模型,逐步培养学生的建模意识和思想。比如针对“销售问题”,笔者设计了这样一个题目:
“足球专卖店中有一种足球的标价为150元,店家为了增加销量,开展促销活动,打八折出售,其销售利润为20%,求足球的进价是多少?”
学生开始解题时会直接用足球的价格乘以0.8计算出打折后的销售价:150×0.8=120(元),再根据20%的利润计算进价:[1201+20%]=100(元)。利润与进价的问题在初中阶段十分常见,这种解题思路就是一种典型的再现性思维,是对以往知识的复习与再现。教师可以借助数学模型培养学生的发现性思维。
分析题目中的已知条件“足球的定价为150元,促销活动是打8折销售,利润为20%。”指出“20%”实际上是商品销售的利润率,其计算公式(利润率模型)为:商品销售的利润率=[售价-进价进价×100%]。利润率模型是一种常见的简单数学模型,因此教师可以引导学生利用这个模型求解。设足球的进价为 x 元,根据利润率模型列出方程:
[150×0.8-xx]=20% ,解得 x=100.
这种解法可以将已知的条件直观地呈现出来,学生通过已知条件构建模型,能更深刻地体会到应用方程解决实际问题的实用性。
接着,对题目进行变式拓展处理,把题目中的“足球的销售利润为20%”改为“这种足球的销售利润降低了30%,但其销量提高了2倍”,问题改为“打折后店家的收益是增加了还是减少了?”或者进一步改变为“这种足球的销售利润降低了30%,为保证店家的利润不降低,销售量需要提高到原来的多少倍?”
改变后的题目,将“进价”隐性化,提高了解题的难度,但对应用利润率模型解题的影响不大,衬托出模型的有效性、通用性,引导学生联系生活,增加学生的经济知识和经营意识。
(二)设计创新性的数学问题,营造良好的课堂氛围
问题是激活学生思维的重要手段,科学的问题设计可以引导学生开阔思维,更好地推进教学活动的开展,因此教师在备课时就要吃透教材,立足教材,结合学生的认知发展情况,设计出具有开放性、启发性的数学问题,引导学生在探索问题过程中强化自身的建模意识。比如下题:“已知市电视台在学校的南偏西54°方向,发射塔建在电视台的正北方向80km处的山上,小陈在学校测得发射塔在学校的北偏西36°方向,求学校到电视台的距离。”
学生解题前,教师先做出提示:“本题中已知条件有哪些?是否能够根据这些已知条件对题目进行简化?”经过思考,学生可以意识到该问题是一个几何模型,要先作图得出一个直角三角形,再运用直角三角形知识求解。这类问题通过构建几何模型使抽象的问题变得直观、简洁,学生理解起来更加容易,解决问题也更高效。
(三)强化学生应用数学模型解决现实问题的意识
数学源于生活又回归生活,初中数学课程涉及很多日常生活中的实际问题,与生活息息相关的数学模型可以强化学生的建模意识,使其认识到数学知识的实用性,激发其学习兴趣。比如在学习不等式的相关内容时,教师可以这样设计题目:
“学校组织学生参加社会活动,旅游公司有大、小两种客车可供租用,每辆50座的大客车日租金为500元,40座的小客车日租金为400元。学校计划租用5辆客车,且要求租金不超过2200元,问:(1)最多可租多少辆大客车?(2)如果参加活动的师生一共205人,请设计出一个合理的租车方案。”
该题目具有多个已知条件,知识点分散,对于学生而言有一定难度,因此教师可以利用表格将已经条件呈现出来。
设租用50座客车 x 辆,根据租金的限制,学生可以列出不等式
500x+400(5-x)≤2200,解得x≤2
根据不等式的解集和实际意义的限制,可确定x的取值范围为0≤x≤2 ,由此得到第(1)题的答案。
第(2)题要考虑人数的要求,可直接利用(1)的模型,列出不等式
50x+40(5-x)≥205,解得x≥0.5
自然数x满足的条件为1≤x≤2,从中可以得出合理(费用最低)方案。
接着,教师可提醒学生注意本题中数据的特殊关系:“两种客车的座位数之比等于租金之比”,只要构建一个不等式模型就可以同时回答两个问题。
[20510]≤5x+4(5-x)≤[2200100],解得1≤x≤2
这种设计既提高了课堂教学的趣味性,又能强化学生的建模意识。
五、初中数学教学渗透建模思想的应用实例
为更好地说明建模思想渗透于初中数学教学中的方法,下面以“解直角三角形”一课为例进行分析。
其一,进行复习回顾,通过复习直角三角形的边角关系引出课程内容,使学生初步了解模型。其二,教师因势利导,抛出以下问题:如何解直角三角形?求解时至少要知道直角三角形中的哪些元素?通过问题引出本节课的教学内容,启发引导学生参照直角三角形全等的判定条件展开讨论,通过对以前学过知识的重新认知,帮助学生充实直角三角形相关的知识体系,梳理和重构相关知识链,为后续构建数学模型打下基础,起到承上启下的作用。其三,教师进一步通过下面的例题设置情境,构建模型。
示例:学校需要测量旗杆的高度,可供使用的工具只有一卷皮尺和一个可测角度测角仪,测角仪的高度为1.5m,请设计一个测量方案并绘制出原理图。
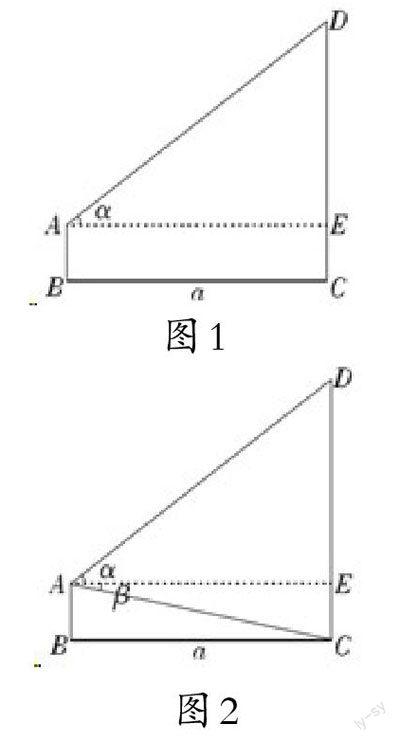
学生容易设计出如图1所示的测量方案:用皮尺测量测角仪AB与旗杆CD的距离CD=a米,用测角仪测得旗杆顶端D的仰角α,由此算出旗杆的高度为(1.5+atanα)米。
这个方案中用到了“已知一角一边解直角三角形”,学生还能设计出其他的测量方案,如测量旗杆底端C的俯角β,通过“atanα+atanβ”计算出旗杆的高度(如下图2所示)。
最后,教师进一步扩建模型:在同样的条件下,你能够测量出上海东方明珠塔的高度吗?
虽然用第一种方案在理论上可以测量出东方明珠塔的高度,但是测角仪的高度仅有1.5m,与东方明珠塔高度相差悬殊,测量仰角和俯角时,会出现仰角过大或俯角过小的问题,产生较大的测量误差,导致测量结果不具有参考意义,而且周边建筑的遮挡也会直接影响测量结果。学生能思考到测量误差的问题,说明学生已经考虑到方案的测量环境的限制,教师继续引导:如果抬高测角仪的位置是否可行?学生容易想到,将测角仪放在另一座高楼楼顶,采用第二种方案进行测量,既减少了误差,又可避免受其他建筑遮挡的影响。
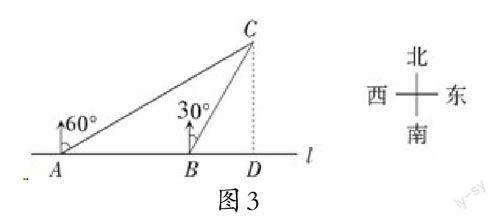
随着对问题的深入探究,学生了解了通过解直角三角形解决实际测高问题的方法,加上环境条件的限制可以引导学生优化测量方案,使学生感受到数学的实用性。此时,教师还需要注意引导学生由解单直角三角形向解具有一定联系的双直角三角形模型过渡,适时引出以下问题(如下图3):
如图3,海岸线上有A、B两个观测点,B在A正东方向20海里处。有一渔船C分别位于A、B的北偏东60°、30°方向上。如果渔船以50海里/小时的速度靠近海岸线,求渔船到达海岸线的最短时间 ([3]取1.7,结果保留一位小数)。
题中隐藏着两个共边的直角三角形,根据双直角三角形的邊角关系,应用方程模型不难求解。教师通过改变点C的位置,可以引出“共边双直角三角形”这一基本图形在实际应用中常见的两种模型(图4)。
有了上面的建模知识储备,教师就可以组织学生开展课后数学活动:用卷尺和测角仪测量电视台建在山上的发射塔的高度,或者仿照上述海岸线观测站观测行船只的情况,利用所学知识设计一套检测汽车行驶速度的方案。最后,组织方案评价活动,评选最优方案。
这一系列问题环环相扣,步步推进,学生真正地体会到解直角三角形相关知识在实际测量中的可操作性和实用性,学生通过参加数学建模实践,获得课堂教学中无法得到的活动经验,促使他们更好地应用数学。
综上所述,在指导学生进行数学建模时,教师要善于引导学生发现现实中与数学相关的问题,帮助他们尝试并最终用数学的语言对问题进行描述,合理选择恰当的数学模型进行刻画和解决问题,帮助学生积累和感悟数学实践的经验,培养学生的科学精神和创新意识。
注:本文为莆田市教育科学“十四五”规划2021年度立项课题“核心素养视角下提升学生数学建模能力的实践研究”(立项批准号:PTKYKT21145)的阶段性研究成果。(作者为课题核心成员)
(邱瑞玲)
