聚焦关键课例 发展关键能力
2022-05-30邓颖洁宋显庆
邓颖洁 宋显庆

《义务教育数学课程标准(2022年版)》(以下简称“新课标”)提出,课程内容重点是对课程进行结构化整合,探索发展学生核心素养的路径。课程结构化整合的背后潜藏的关键词是关联、整体、结构、知識本质。笔者认为,关键课例的研究是落实“新课标”这一变化的脚手架,它不仅是一堂课,更是一种理念,最后落地成一种行为。
一、关键课例的破与立
数学作为一门知识体系严密的学科,我们可以把它看作一棵大树,外在茎干分明,内在脉络通达。如果把这棵树看作意义不同的课,就像特级教师俞正强所说,有一些课“其莳也若子”,需要厘清脉络,有一些课“其置之若弃”,应让学生充分自主学习。那么“其莳也若子”的课,就是有研究价值的关键课例。
关键课例,一般源自知识的起点、节点和拐点,它承载的使命是夯实基础,生长数学思维,发生知识结构关联。或者一句话概括,关键课例的本质就是可供迁移、可供生长。那么,如何来梳理有价值的关键课例呢?一般可以有两个视角:单元视角和知识领域视角。
(一)单元视角
教师在教学中往往会纠缠于碎片化的知识点,存在平均用力、均衡用时的情况。这样就会出现处处是重点、处处又不是重点的情况。教学中,我们可以运用单元视角,锚准单元内容的逻辑顺序,构建符合学情的内容结构,紧抓单元的核心概念,融入基本思想方法。它像一棵富有生长力的种子植根于课堂,生长于学生的头脑中,以操作、体验、交流、感悟等学习方式为主,以结构、方法、思想为目标。比如,人教版数学教材五年级上册“多边形的面积”自然单元中包含平行四边形、三角形、梯形和不规则图形的面积等内容。探究这些内容的过程中都要运用转化的数学思想,在平行四边形面积计算公式推导中,关键的问题是“怎样将一个平行四边形转化为长方形”,但在实际教学中学生的瓶颈问题是“怎么产生平行四边形转化为长方形的想法的”“平行四边形可以转化成长方形是怎么发现的”,这两个问题才是学生的认知症结,也是探究的价值所在。所以在这个单元中,“平行四边形的面积”无疑就成为关键课例,学生在这节课上把问题弄明白了,后续遇到其他图形的面积问题乃至不规则图形的面积问题,就能有效迁移、推理、探究。
(二)知识领域视角
我们可以从鸟瞰知识的角度,了解一个知识板块的来龙去脉、前因后果。小学阶段,由于知识及学情等因素,数学知识在低、中、高年段呈现螺旋上升的形式,这些拆分的知识有些内容相近、结构相似、方法相通,我们可以从跨学段的角度去整体关联、融通,以“瞻前顾后”的策略去思考知识与经验连接的契合点、知识与知识连接的关键点,这些契合点与关键点就是我们需要精雕细琢的关键课例。比如,在“数的认识”这一知识体系中,从自然数到小数、分数等逐渐发展建构。在这个知识体系中,我们梳理出3个关键课例,分别是 “10的认识” “分数的初步认识”和 “用字母表示数”。这3个课例是学生对数的认识发展的不同跨越:10的认识——第一次将学过的数字组合成新数,第一次有“位值”的概念,是自然数认识中知识技能的关键点;用字母表示数——数由确定状态变成了一种未知状态,字母可以用来表示多种情况的数,这是算术思维向代数思维过渡的联结点;分数的初步认识——把一个物体或多个物体看作一个整体,并量化为整数“1”,而这个“1”与自然数“1”的意义的认知跨度是分数认识的起始点,也是数的认识的发展点。
在教学实践中,我们对人教版数学教材进行“全景扫描”,构建单元结构、知识板块图谱,在小学阶段的数学课程内容中梳理出几十个关键课例。在对关键课例的破解中,厘清梳理问题的脉络,形成我们自己的教学主张。
二、关键课例的舍与得
浅显易懂的教学内容,投入时间不需要太多;关键、深刻的教学内容,投入时间往往会多些。随着关键课例实践的深入,对时间的投入问题我们也有了一些新的思考。
(一)舍时间,得顺其自然
关键课例因其在知识结构中的特殊位置和特殊价值,教学时间投入自然相对较多。以“乘法计算”为例,教材编排循序渐进,从乘法口诀、表内乘法、多位数乘一位数到多位数乘两位数,我们把这些内容进行分类(如表1)。
这样分类的数学思考是:第一层次是学习乘法的意义,利用乘法口诀计算乘法。第二层次体现分与合的思想,学生自主将拆数转化为学过的表内乘法,再明确拆成十几和几最简便,最后学习用竖式记录计算过程,充分体会十进位值的意义及其简洁性。第三层次借助积的变化规律将小数乘法转化成以前学过的整数乘法。
所以两位数乘一位数可以看作这个知识体系的关键课例,以“两位数乘一位数”为例,我们这样定位教学目标:
1.理解笔算乘法的算理,学会用竖式计算的方法进行笔算。
2.在多种方法对比中,体会数位和十进位值制在笔算中的重要作用,能够自主选择简洁的方法进行计算。
3.在解决实际问题中学习笔算乘法,感受共性,积累经验,用分与合的方法解决新问题。
教学中,我们设计了以下教学活动:
(1)学生尝试计算 12×3,经历算法多样化。
①12+12+12=36;②2×3=6,10×3=30,30+6=36;
③9×3=27,3×3=9,27+9=36;
8×3=24,4×3=12,24+12=36;
7×3=21,5×3=15,21+15=36;
6×3=18,6×3=18,18+18=36。
通过交流发现:怎么分都可以,都是把 12 分成两部分,分别乘3,再合起来。
(2)出示对比算式:13×3,学生继续自主尝试交流,并逐渐发现:拆成其他数不方便计算,最后发现拆成十和几最好算。
经历了这样不断推翻和建立的过程,学生体会到:在分与合中,按十进位值制去分更简洁,从而帮助学生理解算理。最后通过比较横式与竖式,不断从感官上加强学生对位值的感悟,学生在对比中对笔算乘法的算理逐渐清晰,让思维走向深刻。
关键课例的课堂教学看似花了大量时间,实则为日后学习类似内容储备知识、经验和思维方法。当下的慢是为了将来的快,舍了时间,但争取到了思维生长的顺其自然。
(二)舍功利,得溯源本真
知识分为看得见的知识和看不见的知识。看得见的知识学生摸得着,教师多用讲授的方式,也可以通过练习获得反馈结果。但看不见的知识没有清晰的知识点,学生难以通过自学习得,像“空间观念”之类,教师不能讲,即使讲了,学生也不一定明白。但看不见的知识往往是思想、观念,是素养。在关键课例中应该明确看得见的知识用什么知识点来落脚,看不见的知识靠什么活动去支撑。比如,在“长方体和正方体”单元中,由于长方体的表面积、体积计算的源头是对长方体核心概念的理解以及长方体特征的建构,所以长方体、正方体的认识可作为带动整个单元的关键课例。这个课例中的显性知识不用多说,除此之外,该课还是培养学生空间观念的好时机。教学中除常规活动外,教师还可以拓展以下两个体验活动。
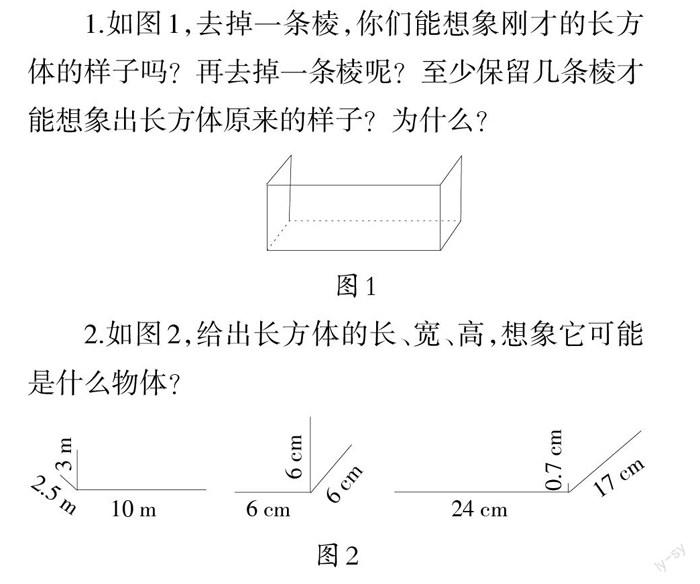
1.如图1,去掉一条棱,你们能想象刚才的长方体的样子吗?再去掉一条棱呢?至少保留几条棱才能想象出长方体原来的样子?为什么?
2.如图2,给出长方体的长、宽、高,想象它可能是什么物体?
如果错失了对空间感的体验,表面上看不会影响学生解决长方体表面积、体积问题,但潜在地会使学生今后主动学习的能力和意识缺失。一个关键课例,舍了功利,抵达了数学的本质。
(三)舍让位,得自主发展
学生是带着已有知识经验走进课堂的,所以读懂学生是关键课例的精髓。我们以关键课例为突破口,以学生的已有知识储备、经验和认知水平为研究对象,对每一个关键课例进行课前测,收集数据并做好数据分析,构建关键课例的学情库。有了数据分析,教师的心中才真的装有学生,才真的懂得让位的智慧。
课堂上,学生已经会的,我们不讲,教师只做“投石人”,去激活与关联。让学生寻找知识与经验、知识与知识的联结点,学会推理迁移,归纳建模。关键课例的课堂上是有声音的:“我是小讲师”体现学生的数学表达,“课堂辩论场”上学生为自己的观点勇敢发声。关键课例的课堂上是有表情的:思考问题时学生眉头紧蹙,动手操作时专注凝神,豁然开朗后眉头舒展。关键课例的课堂上是有思想的:学生圈圈画画,用语言或符号让自己的思维可视化。关键课例的课堂上是有体验的:寻找圆心,自制长方体……我们发现,教师的心里有多少储备,学生的迁移就能激活多少力量;教师手中有多少评价标准,学生的个性就能有多少种呈现形式。
三、关键课例的践与行
如果说关键课例为学生的成长提供了力量,那么,它也赋能教师“破茧成蝶”的专业修养进程。我们构建“3+X+Y”的梯队模式开展课例研磨。“3”是学校导师,“X”是骨干教师,“Y”是青年新秀,不同层级的教师共同磨透一节课,以一节课启发关联课,以一节课磨炼一群人,形成每节关鍵课例的磨课方式:诊断起点(畅聊对教材的理解、对前后知识点的分析),分组研讨(组内研讨、破解疑惑、寻求策略),初磨课堂(在课堂中实践预案),反思重构(反思课堂、策略重构),复盘再上(二次教学、对比分析),集中反馈(以说课的方式集中研讨、分析得与失),形成案例(完善教学资源包,效果不好重回第三环节)。
整个过程人人参与,谁也不是协助者,谁也不是旁观人。就这样,我们“拉长”研课时空,把握教学预设的大方向,积极解决课堂生成中的小问题。同时汇编《“研”近旨远》《“研”为心声》《“研”无止境》等多本专辑,清晰教师专业化成长的轨迹,凝练教师教学素养的培养方法,摸索出一条“以关键课例带动系列课”的特色研究路径。经过打磨,我们给学生提出的问题大胆了一点,让学生学习的步子迈大了一点,给学生思考的时间长了一点,错误中成长的机会多了一点。就这样一点、一点的变化,我们的团队借助彼此的微光去照亮彼此的课堂。经过多年的探索,我们从寻找答案的人,努力变成书写答案的人。
“双减”政策下,如何“提质增效”?关键课例给予了最好的回答。“关键课”不是一堂课,而是一种教育的姿态,也是我们指导学生学习的有效途径。
(作者单位:江西省南昌市站前路学校教育集团 江西省教育厅教学教材研究室)
投稿邮箱:405956706@qq.com
