依托教材资源 浸润传统文化
2022-05-30王宗直
王宗直
教师要注重中华优秀传统文化在数学“综合与实践”领域的渗透,让学生在中华优秀传统文化的浸润中感受文化魅力,培养他们热爱祖国的思想感情。笔者以人教版数学四年级下册《鸡兔同笼》的教学为例,谈谈依托教材资源浸润中华优秀传统文化的教学策略。
一、以史激趣,感受中华优秀传统文化的魅力
上课伊始,笔者以《孙子算经》中的数学趣题切入,以史激趣,激活学生思维:从古到今,我国有许多人喜欢数学并成了了不起的数学家,创造了举世瞩目的数学成就。1500年前,一部名为《孙子算经》的数学著作中记载了许多有趣的数学问题。今天我们一起来研究其中的一道数学趣题——“鸡兔同笼”问题。
然后,笔者利用多媒体课件出示教科书第103页的主题图及“鸡兔同笼”原题:今有雉兔同笼,上有三十五头,下有九十四足,问雉兔各几何?这道题一共有24个字,却像诗歌一样娓娓道来,表达简洁明了,问题要求明确。笔者让学生读一读题目,感受古文的魅力,并尝试说一说题目的意思。
本节课用数学史料导入,笔者在介绍《孙子算经》时,暗示学生本节课要研究书中记载的许多趣题中的一道。这个暗示不但激发了学生的学习兴趣,而且使学生感受到我国数学文化的源远流长、丰富多彩,增强了学生的文化自信和民族自豪感。
二、合作探究,体现中华优秀传统文化的价值
在这个环节,笔者引导学生围绕“鸡兔同笼”问题展开讨论、交流,体验数学建模的过程;引导学生在题型结构、解题方法上进行分析、比较和推理,感受古代数学的趣味性及其文化影响力。
首先,笔者出示例题1,鼓励学生用自己的方法尝试解答:“笼子里有若干只鸡和兔,从上面数,有8个头,从下面数,有26只脚。鸡和兔各有几只?”
汇报时,学生分别展示了如下3种解题方法。
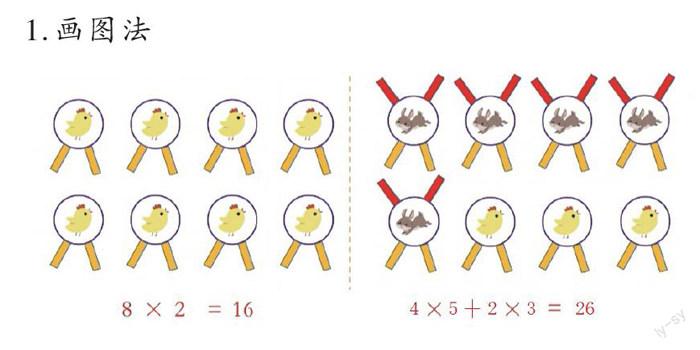
1.画图法
学生甲汇报:“我用画图的方法算出了鸡和兔各有几只。先画8个圆表示鸡和兔的头数,假设全部都是鸡,就在圆下面画2只脚,结果总共只有16只脚,比题干上的26只脚少了10只,说明不全是鸡,还有兔。然后我就在5只鸡的圆上分别添上2只脚,把5只鸡变成了5只兔子,这样8个头、26只脚都凑齐了。由此得出有5只兔和3只鸡。”
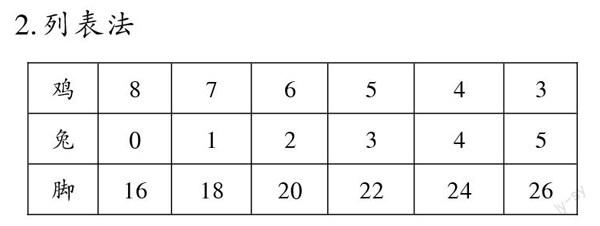
2.列表法
学生乙汇报:“我们小组共同用表格法找到了答案。如果是8只鸡、0只兔,则共有16只脚,不符合题目条件;如果是7只鸡、1只兔……直到有3只鸡、5只兔,共有26只脚,才符合条件。所以从表格中就可以看出鸡和兔各有多少只。”
3.假设法
学生丙这样阐述:“我用的是假设法,可以假设全是鸡,也可以假设全是兔,我这里假设全是鸡,但8只鸡只有16只脚,看来假设有误,其中有一些不是鸡而是兔。用多少只兔来换鸡才能将16变成26呢?因为1只兔换1只鸡,增加2只脚,现在16与26相差10,所以要用5只兔来换5只鸡,进而求出鸡有3只、兔有5只。我先计算‘26-8×2=10,再求出兔的只数是‘10÷(4-2)=5只,鸡的只数是‘8-5=3只。”
笔者对学生的汇报进行总结后,再次呈现开课时《孙子算经》里的题目,让学生选择喜欢的方法自主解答:“今有鸡和兔关在同一个笼子里,从上面数有35个头,从下面数有94只脚。问鸡和兔各有多少只?”学生有用画图法和列表法的,也有用假设法直接求解的。交流时,学生发现题中的数目变大了,用画图法与列表法解答很麻烦。那么,古人是用什么方法解决这一问题的呢?笔者结合教材内容给出相关资料,引导学生阅读并提问:800年前,元朝数学家丁巨在他的《丁巨算法》中提到假设法,不过古人那时候用的假设法与我们今天的方法不一样,你知道他是用什么方法解决的吗?一名学生回答:“从资料内容看是‘半足法,就是先把脚数除以2,这样兔就剩下一半的脚,兔的脚数就是只数的2倍;鸡也剩下一半的脚,与鸡的只数相同。用总只数减去总头数就可以得到兔的只数,进而得出鸡的只数。”
笔者充分利用教材的辅助资源,挖掘其文化内涵进行教学,既深化了学生对“鸡兔同笼”问题的理解,又凸显了古人解决数学问题的智慧,体现了数学的育人价值。
三、总结提升,弘扬中华优秀传统文化的内涵
方法的习得只是这一节数学实践课的浅层要求。学生知其然,但未必知其所以然,所以,揭示其算法的本质才是这节课高层次的要求,能引导学生从完成建模到能力塑造。
笔者首先介绍:“我们用今天的方法解决了古人提出的‘鸡兔同笼问题。大家可曾知道这享誉古今中外的趣题、趣法传到日本后,问题的主角從鸡和兔变成了仙鹤和乌龟,演变成了日本的‘龟鹤算问题。看来‘鸡兔同笼问题的主角不一定就是鸡和兔。”然后,笔者出示一道类似的题目让学生尝试完成:一个停车场有小汽车(四轮)和摩托车(两轮)共24辆,这些车共有86个轮子,小汽车和摩托车各几辆?这道题和“鸡兔同笼”有什么相似之处呢?笔者引导学生分析题目信息发现:所求的两个问题答案之和都是已知的,题目都从不同角度给出了与两数之和相关的信息,题目中暗藏了一个差数(如小汽车与摩托车车轮数之差),这个差数是解决问题的关键条件。通过笔者的进一步引导,学生明确:古人的“倍头法”和“半足法”就是要造成一个新的差数,新差数与题目中差数相除即可求解。也就是说,假设把每辆车都拆掉两个轮子,那么摩托车没轮子了,汽车只剩下两个轮子,总轮子数减去拆掉的轮子数就是汽车所剩的轮子数,再除以“2”就可得到汽车有“(86-24×2)÷2=19”辆,进而得出摩托车有“24-19=5”辆。最后,笔者揭示:研究“鸡兔同笼”的一般解决方法,并把它作为一个模型,就可以解决生活中更多类似的问题,如租船问题、购物问题、植树问题等。
中华优秀传统文化博大精深,要将其融入数学课堂,教师需要根据教学内容对其进行精心选择、精心设计,恰如其分地渗透,让文化触及学生心灵、启迪学生智慧,增添学生学习数学的信心。
(作者单位:松滋市陈店小学)
责任编辑 张敏
