弘扬数学文化 彰显育人价值
2022-05-30周静
周静
数学文化既可指数学的思想、精神、方法、观点、语言,以及它们的形成和发展过程,也包含数学史、数学美、数学与人文的交互、数学与各种文化的关系等。把数学文化融入数学教学中,可以使数学课堂拥有更加深厚的文化底蕴,激发学生学习数学的兴趣,培养学生的文化素养,强化学生的数学理解,促进学生形成正确的数学观。本期,我们来讨论如何将数学文化更好地融入数学教学中。
《义务教育数学课程标准(2022年版)》强调“关注数学学科发展前沿,继承和弘扬中华优秀传统文化与数学文化”。在素养导向下,数学教学更需要凸显数学文化的价值。如何将数学文化融入初中数学教学中,彰显文化的育人价值呢?
一、引入数学史料,丰富文化内涵
中华民族孕育了灿烂的数学文化,历史上出现过刘徽、祖冲之、赵爽等伟大的数学家,有《九章算术》《孙子算经》《周髀算经》等经典之作。教师充分利用这些资源,将与教学内容有关的数学史话和故事融入教学中,有助于学生了解数学知识生成的过程,感悟古人智慧,丰富自身文化内涵。
如在《正多边形和圆》的教学中,教师在引导学生探究圆周率时,向学生介绍了刘徽发明的“割圆术”(刘徽推算出π约等于3.14)。学生理解了“割圆术”后,教师引入阅读资料“公元5世纪,祖冲之进一步推算出π值在3.1415926与3.1415927之间……他是第一个将圆周率精确到小数点后7位的人,这比欧洲早了一千多年”,使学生感悟到我国古人的智慧,强化了民族自豪感。在拓展环节,教师播放介绍圆周率计算的发展及应用的视频,使学生了解到“21世纪初,科学家已经计算出π的小数点后超过万亿的位数”,“π的计算成为测试超级计算机性能的方法之一”等,明确了圆周率是无限不循环小数,借助它可以进行关于圆和球体的各种计算,其数值的“准确性”直接影响有关计算的精确度,这就是人类求索圆周率的原因。丰富史料的引入,使学生开阔了眼界,丰富了对圆周率的认识。
二、传承经典游戏,促进文化理解
教师在教学中融入经典数学游戏,有助于学生提升学习兴趣、巩固所学知识、深化对知识背后文化内涵的理解,能促进学生数学核心素养的提升。
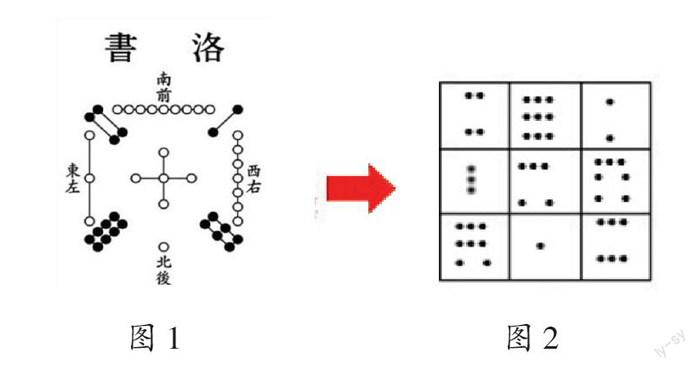
为了使学生更好地掌握有理数的加法运算、进一步理解相反数的意义,在教学“有理数的运算”相关内容后,教师设计了实践活动课,向学生介绍了关于幻方的历史,并组织学生开展了填幻方游戏。课上,教师出示世界上最早的幻方图——“洛书”数字图(如图1),以及由“洛书”数字图演化而来的幻方图(如图2,每一行、每一列以及两条对角线上的格子中点数的和都是15),引导学生照样子将“-4、-3、-2、-1、0、1、2、3、4”分别填入9个空格中,使处于同一行、同一列及两条对角线上的3个数相加都得0。
学生自主填幻方并交流后,汇报了多种填法,同时他们发现:虽然数字填写的方案不唯一,但正中间格子中的数一定是“0”,且经过“0”的那一行、那一列及两条对角线上的另外两个数互为相反数。学生在浓厚的文化浸润中学习数学,深化了对知识及其背后数学文化的理解和运用。
三、强化数学探究,感悟文化价值
教师要重视学生获取知识的思维过程,帮助学生经历知识的“再创造”,体会数学的发展既是数学本身的需求,也是社会发展的需要,进而感悟数学文化的价值。
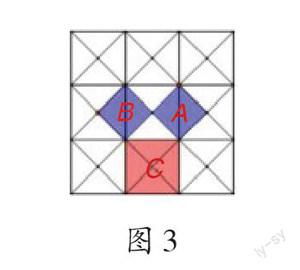
如教学《勾股定理》时,教师设计了“地砖探秘”“填表猜想”“拼图证明”三个数学活动,逐步引导学生探究勾股定理。教师首先从毕达哥拉斯的“地砖探秘”引入,出示图3(假设图中每个小三角形都是等腰直角三角形且面积为1)并提问:图中三个正方形A、B、C的面积分别是多少?它们的面积之间有什么等量关系?学生观察发现“[SA=SB=2]、[SC=4]”,得出“[SA+SB=SC]”。
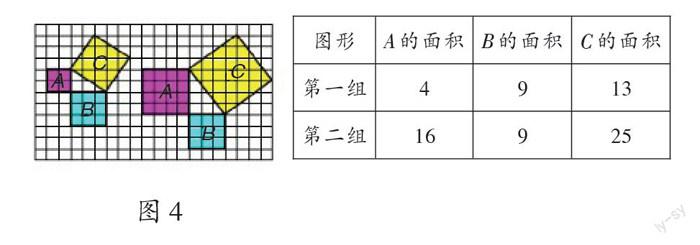
接着,教师提问:由这三个正方形的边长构成的等腰直角三角形的三条边的长度有怎样的关系?学生计算后发现“A的边长与B的边长的平方和等于C的边长的平方”。这个关系是在特殊的直角三角形的条件下得到的,为了引导学生经历由特殊到一般的推理过程,教师质疑:“如果是一个任意的直角三角形,这个结论还能成立吗?”教师出示格子图(每个小方格的面积均为1),引导学生在格子图上确定一个任意直角三角形,以直角三角形的三条边(a、b、c)为边长向外作三个正方形A、B、C,并探究这三个正方形面积之间的等量关系。学生探究后,教师呈现学生的两个作品(如图4),并将学生完成的两组数据填入下表。
学生通过分析得出“[SA+SB=SC]”,并利用面积关系推算出直角三角形的三边关系“a2+b2=c2”,归纳出“直角三角形两直角边的平方和等于斜边的平方”。
为了验证这一猜想的正确性,教师让学生拿出课前准备好的4個全等的直角三角形纸片(两条直角边边长分别为a、b,斜边长为c),引导学生用这4个直角三角形拼一个正方形,观察拼的正方形中是否含有以c为边的正方形。学生小组合作探究,呈现了多种拼法,如方法1(图5)与我国古代数学家赵爽“弦图”的证法相同,方法2(图6)与外国数学家毕达哥拉斯的证法相同。
展示过程中,教师乘机引入对赵爽和毕达哥拉斯证明方法的介绍,使学生明确了“勾股定理”的由来。此外,教师还出示了毕达哥拉斯根据“勾股定理”画出来的树形图——“毕达哥拉斯树”,丰富学生的认知。这样教学使学生像古代数学家一样发现并证明了勾股定理,感悟到数学文化的价值。实际上,勾股定理还有很多种证明方法,教师可引导有兴趣的学生收集相关资料,加深对勾股定理的理解。
四、渗透数学之美,尽享文化魅力
数学具有独特的美学价值,在数学教学中融入多方面、多角度的美学展示,能让学生感受数学知识背后丰富的文化内涵,感悟数学文化的魅力。如:教学《黄金分割》时,教师可引入“蒙娜丽莎的微笑”“希腊帕特农神庙”“埃及金字塔之谜”等相关素材,让学生直观感知“黄金分割”所带来的美感;教学《轴对称图形》时,教师可引入剪纸作品、京剧脸谱等学习资源,引导学生发现传统艺术中的对称美;教学《投影》时,教师可让学生欣赏皮影戏视频,感悟皮影艺术中蕴含的数学知识及其美学价值。
(作者单位:黄冈市外国语学校)
责任编辑 刘佳
