应用知识空间理论探究中学生的关键学习路径

陈文梅 陈博

摘要： 应用知识空间理论构建学生在化学方程式知识的关键学习路径，了解不同类型学校九年级493名学生中大单元“化学方程式”构建知识结构的层级关系。研究发现，不同类型学校的学生群体的关键学习路径有所差异，专家期望的知识结构与学生实际知识结构之间存在差异。最后建议教师应了解学生潜在知识状态并给在学习路径末端的概念适当补救教学，降低学生概念层级。

关键词： 知识空间理论; 关键学习路径; 化学方程式

文章编号： 10056629（2022）09002405

中图分类号： G633.8

文献标识码： B

1 问题的提出

Doignon和Falmagne[1]在1985年提出的知识空间理论（Knowledge Space Theory，简称KST）是一种基于组合和概率模型、被用来评估学习者学习状态的理论，它既融合了测量学的部分内容，又融合了心理学的相关内容，被视为当前研究的热点问题。

国外研究者已应用知识空间理论进行一些教学研究，但研究数量较少，研究侧重于物质结构和化学计算方面[2，3];国内研究者曾应用知识空间理论用于高中的氧化还原反应和离子反应的新课研究[4]，尚未见应用知识空间理论对初中的学生进行研究，也尚未见应用知识空间理论研究学生在复习课后的知识结构。化学方程式既是初中化学启蒙教育阶段学生应该掌握的最重要化学用语，又是化学反应的具体表现形式，更是学生学习化学的重要工具。因此，有必要应用知识空间理论分析九年级学生在复习课中化学方程式的学习情况。

2 知识空间理论

知识空间理论是由心理学家Doignon和Falmagne基于数学的集合和心理学所提出的一种诊断知识和能力的理论，主要包括学习路径（Learning Path）、知识状态（Knowledge State）、知识结构（Knowledge Structure）、知识空间（Knowledge Space）等基本概念[5]。

Doignon和Falmagne等人认为知识在学生认知结构中的组织是通过良好的知识结构来描述的，他们将某领域的知识看成学生具备该领域的必备知识和关键能力才能解决的问题，某领域为相关问题的集合Q，考查单一或需要了解、记忆等低阶思维便可以解决的问题称为低层次问题，而考查高度概括化的知识或需要推理创新等高阶思维活动才可以解决的问题称为高层次问题。知识间具备较强的逻辑关联性，假如学生可以解决高层次的问题，可以推测学生可以解决低层次的问题，这种关系称为问题间的推测关系。

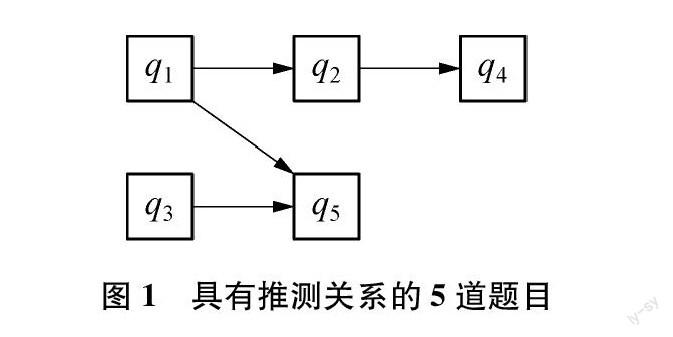
以Doignon和Falmagne等人的例子进行简单地阐释，现在有5道具有推测关系的数学题（见图1），箭头表示由低层次的问题指向高层次的问题，第4题是第2题的高层次问题。这些问题可以按照任何排列顺序让学生去作答，学生正确回答的一组问题称为知识状态。例如，正确回答问题1、 2和4的学生处于知识状态[1， 2， 4]，所有问题都回答错误记为空集，所有问题回答正确记为全集Q。对于测试493个学生，最多有493个响应状态，但通常只观察到10～15个知识状态。

从所有可能的知识状态中，KST使用χ2分析拟合并识别出大约10个知识状态的子集称为知识结构，该子集代表了所有的学生作为一个整体。其中每个知识状态（除了空集和全集Q之外）都有一个前一状态和一个后续状态，并且每个连续状态都比前一个状态多一个问题即结构必须具有良好的分级，如以、{q3}、 {q1， q3}、 {q1， q2， q3}、 {q1， q2， q3， q4}、 Q这种在具有在知识逻辑性基础上依次增加一道题的方式构成一条路径称为学习路径;然后从最密集的知识状态开始，加减知识状态以最小化χ2拟合值，知识状态最后构成多条学习路径从而形成一个知识空间（Knowledge Space）的示意图（见图2）。

图2能够清楚地反映作答者的心理知识构建的先后次序，作答者先解决低层次问题，再解决高层次問题。知识空间理论将所有作答者的作答情况进行概率计算，在知识空间示意图中出现次数最多、概率最大的，称为关键学习路径，即在学习过程中最可能出现的学习路径。该学习路径在开展后续研究以及生活中有着重要作用。知识空间理论（KST）可以测量学生在建立基本化学原理或基本概念之间逻辑联系的能力。知识空间理论还可以用于不同的学科，便于教师了解学生的知识状态，对于后续教学的评估起着举足轻重的作用。

3 研究方法

3.1 研究对象

根据广州市最近几年各初中中考成绩，笔者将广州市初中划分为3个类型的学校，不同类型的学校的学习成绩具有显著差异，第一类初中是中考成绩非常优秀的初中，其他类型的学校依次次之。同一类型初中培养出相近能力的学生群体，不同类型的初中培养出不同能力的学生群体。为了解广州市不同类型九年级学生在化学方程式知识的学习结果，笔者使用群体抽样的方法，在第1～3类初中，每个类型随机选取2～3所学校，在每所学校中随机抽取九年级2个班，每班男生和女生人数相近。最后，7所初中14个普通班共493名学生作为研究被试，本测试的时间临近中考，复习课正在进行中，每个学生的掌握程度不同。因此，学生复习专题测试的表现，可以视为学生学习化学方程式的最终学习结果。

3.2 研究工具

组织3位专家（1位化学教研员，2位广州市初中化学中心组成员）共同研讨，根据学生的认知发展顺序、教材的编写顺序和知识逻辑结构的顺序，整理出“化学方程式”大单元的核心概念。即节点1： 理解质量守恒定律;节点2： 化学方程式的意义;节点3： 判断化学方程式书写是否正确;节点4： 书写简单的化学方程式;节点5： 书写复杂的化学方程式;节点6： 化学方程式中的定量关系;节点7： 化学方程式的计算。

笔者与3位专家共同研讨，提出一个体现学生化学方程式知识和能力发展顺序（即以难度增加顺序对问题进行排名的原理）、可能经历的化学方程式学习过程，最终得出专家认为的关键学习路径为1→2→3→4→5→6→7。认为质量守恒定律是正确书写化学方程式及利用化学方程式计算的基础;化学方程式的计算是前几个概念的上位概念，学生应该是从单一的概念到关联性的概念发展，从定性到定量、宏观到微观的认知发展，逐渐建立宏观、微观、符号和数量的之间的关联性。比较专家期望学生所拥有的知识结构与学生在考试中展示的真实知识结构之间的差异，了解知识空间，有助于教师、新课标和教科书等对概念组织或教学策略进行调整。

笔者与3位有丰富九年级化学教学经验的中学高级教师严格按照课程标准、中考要求和研究目标来编制测试题，测试题目一共7道，遵循从简单问题到复杂问题的分级过程，后一个问题基于前一个问题的理解，以遵循学生的认知组织顺序，分别对应化学方程式关键学习路径的7个节点，测试题的难度与课标学业要求和中考要求相对应，科学设置试题的难度，体现较好的区分度。试题内容符合九年级学生的学习要求，有较好的内容效度。通过用SPSS软件分析测试题各题得分与总分均存在显著相关（p<0.001）。

3.3 研究流程

本研究使用化学方程式测试题，收回测试题后，先进行批改，以二进制方式对答案进行评分，如果是正确答案的代码，赋予1分，如果是错误答案的代码，赋予0分。接着导入SPSS软件中计算各道题的答对率和总分，用方差分析比较总分是否有显著性差异且用卡方检验比较各类型初中的学生在答对、答错的人数的分布上是否有显著性差异。

3.4 数据统计

将学生在每道题的得分情况用0和1表示为有序的数字组合，得到每个学生的作答的反应模式，例如1011001、 1101011、 1111011等，然后统计不同反应模式类型的数量及相应出现的次数，记录于TXT文件中（如图3所示，其中Q1， Q2， Q3等分别代表问题1、 2和3等，“1”代表正确答案，“0”代表错误答案，N是相同回答状态的学生人数），为KST的程序构造第一个输入文件（KST1.TXT）;例如在第三类型的学校中，共有28种反应模式类型，其中1000000有1人次，1011000有16人次，应用麦裕华等人[6，7]自主开发的KST统计程序软件包读取KST1.TXT文件的数据后，得到KST程序中的输出文件，统计学生反应模式的种类、出现概率和推断出必要的反应模式，计算出各类型初中的知识空间图和关键学习路径。

笔者利用以上的数据和图形分析比较学生实际的关键学习路径与专家的关键学习路径的差异，得出学生化学方程式的学习结果。

4. 结果与讨论

4.1 学生的答题情况

本次测试题的总分是7分，如表1所示，不同类型学校的平均分在4.82～5.92之间，其中平均分按照第一、二、三类型学校的顺序依次降低，体现了不同类型学校的差异性。对各个学校的测试总分进行方差分析得出F=44.110， p<0.001，结果显示三个类型学生的知识结构有显著差异，第一类型学生群体的知识结构比第二类型和第三类型学生群体的知识结构好，第二类型学生群体的知识结构比第三类型学生群体的知识结构好。结果启示教师要引导学生从微观角度孤立分析化学方程式的基本概念上升到联系的角度，从定性层面上升到定量层面，逐渐完善学生的认识思路和思维方式。

4.2 学生的关键学习路径

应用KST统计程序分别计算出不同类型学校学生的关键学习路径，结果如表2所示，其中箭头代表知识层级间从低到高发展，逗号代表知识在学生脑海中的层级间属于平等关系。

根据表2分析，在不同类型学校的学生群体的关键学习路径中，后半部分表现出一致性的特点，说明学生认为定量的认识方式是定性认知方式的高层次问题;前半部分存在较大的差异性，第一类型学校的学生群体先是掌握理解质量守恒定律（节点1），然后是同时掌握判断化学方程式是否正确（节点3）和简单的化学方程式的书写（节点4），说明这两个概念在学生群体的脑海层次结构中处于同等的独立的认知结构;而第二类型学校的学生群体先是掌握简单的化学方程式的书写（节点4），然后学会判断化学方程式书写是否正确（节点3），再掌握理解质量守恒定律（节点1）;第三类型学校的学生群体先是掌握理解质量守恒定律（节点1），再掌握简单的化学方程式的书写（节点4），最后学会判断化学方程式书写是否正确（节点3）。

第三类型学生群体的节点1和节点4与第二类型在关键学习路径中的出现次序相反;其原因可能是不同类型学校的学生群体的学习能力不同、教师的教学方式不同、教师的学科知识不同和学习素材不同。最后的四大节点中，三个类型学校的学习顺序都相同，先出现节点7，而专家认为节点7应该在掌握前面6个节点之后再出现，学生需要在掌握前6个节点的基础上才能解决节点7，因为它要求学生经历解题和设不带单位的未知量，写出相应正确且已配平的化学方程式，接着是分析题干、计算并写出相关物质的相对分子质量和已知量、未知量，并标在化学式和相应相对分子质量下面，然后是列比例式求解，最后是简明地写出答案，专家认为以上解题步骤复杂需要最多的心理加工过程，而节点7在学生的认知结构中出现得较靠前，可能是因为学生已通过大量的练习或者采用机械记忆的方法去学习它。接着出现的是节点6，它要求学生找准已知量，列相关的比例式解答。学生先掌握简单化学方程式的计算（节点7），再学会化学方程式的定量关系（节点6），其原因可能是学生对有固定模式的题目训练多，且是中考必考的题型，而在抽象化学方程式下确定定量关系在中考中出现的少，学生训练得少，虽然解决节点6和节点7这两个问题的思路是相似的，但节点7要求学生在正确书写出相关的化学方程式的情况下才可以进行计算，这一点在节点6没有体现。

通过与专家的关键学习路径进行比较，笔者发现，各类型学生的关键学习路径和专家的关键学习路径不同，说明学生脑海里的知识结构和专家的知识结构不一样;学生认为节点5学会书写复杂的化学方程式是最难掌握的知识点，而专家认为节点5应在节点6前掌握;节点5要求学生能够理解复分解反应的条件下采用类比的思想进行解答，这要求学生具有较多的心理技能和较高的高阶思维能力。由此可见，专家期望的知識结构与学生的实际知识结构之间存在显著差异，建议教师在了解学生的潜在知识状态的基础上，对出现在路径末端的需要心理加工程序较多和繁杂的概念及时通过模型构建、类比策略等方式降低学生的概念层级，提高学生在心理加工过程中融会贯通的思维能力。

5 结论与启示

5.1 研究结论

研究构建广州市三个类型共7所学校的九年级493名学生的化学方程式知识的知识结构，发现不同类型学生在化学方程式的核心知识上有不同的表现，在测试总分上存在显著差异，在知识状态的数量、知识空间的结构上存在较大差异;不同类型学生关键学习路径的节点出现顺序不相同，表现出不同的关键学习路径，且和专家的关键学习路径不相同。

5.2 教学启示

针对广州市不同类型初中学生的关键学习路径不同，可以说明不同类型的学生的能力各异。因此，补救教学需正确对待学生群体的差异，建议教师在备课期间，可以参考关键学习路径进一步调整和优化教学顺序。能力欠佳的学生在学习书写化学方程式时，难以将其化学式书写出来，而判断化学方程式是否正确需要的心理加工过程较少，因此教师在计划复习课教学时，把在知识节点排位靠后的概念作为复习的重难点，可采取模型认知、类比和大概念等策略进行教学，巩固学生的认知路线。如在化学方程式教学中，应将书写复杂的化学方程式作为复习的重难点。

5.3 研究展望

研究所选取的对象仅限在广州市的研究被试，仅静态地反映学生在复习课期间学习化学方程式的知识结构及其内在关系（概念之间是怎样联系的）。研究仅采取一次测试，并未充分反映学生在教师进行补救教学后学习化学方程式过程中动态的知识结构的变化过程（通常涉及概念转变），探究教师进行补救教学的策略的有效性。在未来的研究中可以通过前、中、后多次测试反映学生的知识状态、知识空间图动态变化过程，以跟踪学生的概念理解的发展，检验教师的补救策略的效果;也可研究不同地域、不同年级的学生学习的结果，还可以探究初中生在化学方程式知识掌握上是否存在性别差异。

此外，题目的难易程度会影响学生路径结果，造成误差。因此，如何选择并优化基本的属性层级，以提供更加精确的诊断结果，也是一个值得深入探讨的问题。

参考文献：

[1]Doignon J-P， Falmagne J-C. Spaces for the assessment of knowledge [J]. International Journal of Man-Machine Studies， 1985， 23（2）： 175～196.

[2]Segedinac M. T， Horvat S， Rodic′ D. D， Ronc evic′ T. N， Savic′ G. Using knowledge space theory to compare expected and real knowledge spaces in learning stoichiometry [J]. Chemistry Education Research and Practice， 2018， 19（3）： 670～680.

[3]Falmagne J-C， Albert D， Doble C， Eppstein D， Hu X （Eds）. Knowledge spaces： applications in education [M]. Berlin： Springer-Verlag， 2013.

[4][7]何庆辉， 麦裕华， 基于知识空间理论的高一学生离子反应关键学习路径[J]. 化学教学， 2018， （7）： 12～17.

[5]Falmagne J C， Koppen M， Villano M， et al. Introduction to knowledge spaces： How to build， test， and search them [J]. Psychological Review， 1990， 97（2）： 201～224.

[6]課程教育研究所， 化学课程教育研究开发中心.义务教育课程标准实验教科书·化学（九年级上册）[M]. 北京： 人民教育出版社， 2012： 99～101.