SOLO分类理论在我国数学教育研究中的应用述评

2022-05-30高瑞荣霍庭芸

数学教学通讯·高中版 2022年10期

高瑞荣霍庭芸

［摘要］对国内数学教育研究领域应用SOLO分类理论的96篇（2000—2020年）文献进行文献计量与内容分析，发现：该理论经过介绍引进、尝试应用、融合创新阶段后，在数学认知水平评定、开放题研究、中高考题研究、问题提出与解决能力研究、课堂教学实践指导等方面有广泛应用. 已有的研究广度有余、深度不足，对相关工具的信度和效度分析不够. 未来应重视将理论在认知研究中的成果与数学课程、教学目标进行整合，加强理论与数学教学实践相结合的行动研究，提升数学教学实践者应用SOLO分类理论的能力.

［关键词］ SOLO分类理论；数学认知水平；数学开放题；数学问题提出与解决；数学课程与教学目标；数学教育评价

[?]问题提出

SOLO（Structure of the Observed Learning Outcome）意为“可观察的学习成果的结构”，是澳大利亚学者比格斯（Biggs，J.B）和科利斯（Collis，K.F）创建的一种描述学习者在学习过程中的思维结构框架［1］. 在此基础上形成的SOLO分类理论，是研究者根据学习者的学习成果对其思维结构进行质的分类评价方法的理论基础. 该理论引入国内以来，许多研究者以此开展了大量的理论介绍和实证研究，并就国内相关研究进行述评［2-3］.

随着数学教育研究者对该理论的全面介绍、了解、尝试应用以及数学新课程改革对学生学习过程评价的重视等因素的影响，SOLO分类理论应用于数学教育领域的研究成果逐渐增多. 本文拟对SOLO分类理论应用于数学教育的研究进行系统总结，分析其研究现状，厘清存在的问题，为SOLO分类理论能在数学教育实践和学术研究中有更广泛的推广和应用提供启示.

[?]SOLO分类理论简介

比格斯等认为人的认知不仅在总体上具有阶段性的特点，在对具体知识的认知过程中也具有阶段性的特征，从而在皮亚杰的认知发展阶段论基础上进行扩充形成SOLO分类理论（SOLO TAXONOMY）. 研究者依据该理论可将学习者的学习成果的认知结构由低到高具体划分为前结构、单结构、多点结构、关联结构和抽象扩展结构五种层次，分别代表被评价者对知识的掌握水平和理解层次［4］. 具体说明如表1所示.

同时，由于SOLO分类理论模糊的结构概念会导致分类的不稳定和发生将“扩展抽象”认为是“前结构”的误会. 伯内特（Burnett）对比格斯等的SOLO理论进行了改进，在SOLO分类理论的多点结构和关联结构中各加入了三个次层次，将学习成果划分为九个层次（见表2）［5］. 这使SOLO分类理论的评价功能更加准确和完善.

SOLO分類理论作为一种学习结果的评价工具，以更微观的视角对学生学习过程的思维层次进行评级，这为研究者通过评价学习者的具体学习成果而展开更广范围的研究提供了坚实的理论基础.

[?]研究方法

本文拟采用文献计量法和内容分析法，通过中国知网数据库，具体以“SOLO分类理论”或“SOLO分类法”或“SOLO”为检索主题词并含“数学”“数学教育”进行精确数据检索. 依据搜索结果发现，我国对SOLO分类理论在数学教育中的应用研究成果在期刊中较早出现于2002年，发文量逐年呈递增趋势，与研究的相关主题不断扩展. 本文将文献筛选年份设定为2000年1月至2020年12月，通过反复查询筛选权威期刊文献、学位论文和会议论文，剔除重复研究、书目公告，共获得96篇文献，其中期刊论文30篇、硕博士学位论文66篇. 通过对文献内容的整理与分类，拟从SOLO分类理论在数学教育中应用研究的趋势、层次与内容进行分析.

[?]研究结果

1. 应用研究的趋势分析

通过梳理研究指定年份内发表的文献对SOLO分类理论在数学教育中的应用研究成果，从年份文献量指标来看，20年内相关研究的文献量整体呈上升趋势. 从应用历史来看，大致可分为“引进介绍”“尝试应用”与“融合创新”三个阶段. 自SOLO分类理论引进国内数学教育研究领域以来，研究者较多致力于“理论+案例”的介绍工作［6-7］，通过对案例的分析，加深数学教育工作者在数学教育中应用SOLO分类理论的认识与理解；“尝试应用”主要表现为研究者通过第一阶段的认识与理解，结合个人经验，对SOLO分类理论在数学教育中的应用进行更为深入的探究［8-10］；随着时间的推移，“融合创新”的应用研究成果明显增多，从认识与理解到深入探究，研究者对于该理论的研究分析逐渐转向实践层面，将SOLO分类理论作为自己的研究理论基础之一展开规范研究.

2. 应用研究的层次与内容分析

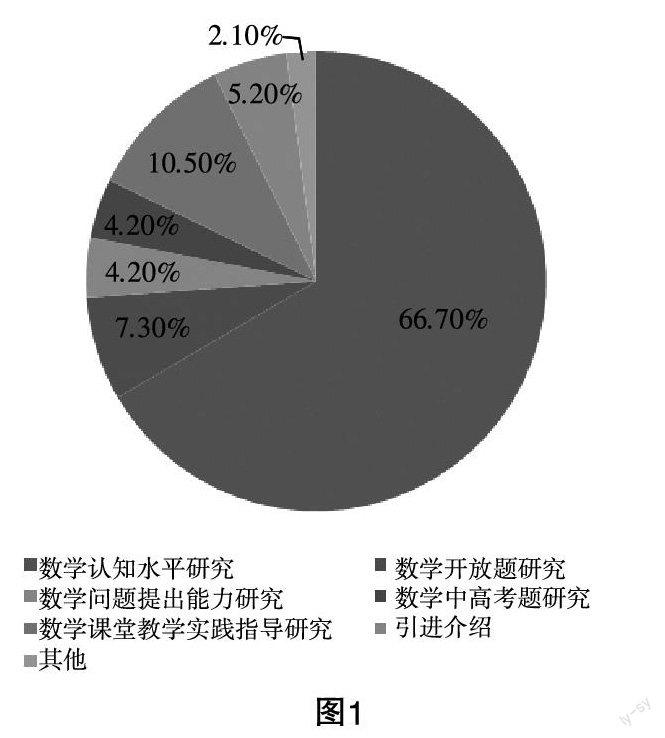
应用研究的层次与内容具体指SOLO分类理论在不同数学教育研究领域中的具体分布. 通过对96篇文献的分析，具体分布如图1所示.

从内容分布来看，SOLO分类理论在数学认识水平、数学开放题、数学问题提出能力、数学课堂教学实践指导、数学中高考题等研究领域均有应用；从数量分布来看，SOLO分类理论在数学认识水平研究领域居多，其次是数学课堂教学实践指导、数学开放题和数学中高考题等领域的相关研究.

（1）应用于数学认知水平的研究

基于具体知识、观念和素养发展过程的阶段性特征假设，研究者依据SOLO分类理论来编制测试工具以及划分和评定被研究者的数学认知水平，进而获取相关数据开展研究. 如较早对概率认识水平［11］和数学解释水平的研究［12］；随后对导数理解［13］、向量概念［14］、算法［15］、函数［16］等一系列数学基础教育内容的认知和理解水平的研究，甚至涉及数学高等教育内容如群概念的理解水平等［17］. 研究者也借助SOLO分类理论在如空间观念［18］、数据分析观念［19］、数学实验观念［20］等认知领域建构观念测量框架，体现了对SOLO分类理论的融合创新应用. 同时，依据SOLO理论的数学认知水平研究涉及对象包括少数民族学生［21］、师范本科生［22］、在职数学教师群体；除去具体数学内容外，对数学素养［23］、数学史素养［24］等素养水平的研究均以SOLO分类理论为理论基础. 这些研究有对SOLO五层次模型的直接应用，也有嫁接选择三层次、四层次乃至七层次的研究框架. 研究成果对数学教学、教师专业发展均可提供一定启示.

当然，以SOLO分类理论为理论基础的数学认知水平实证研究需要良好的研究设计，在测试工具与评分过程乃至数据处理方面需要严格要求. 这样才能对研究成果再吸收，才可以展开学术对话.

（2）应用于数学开放题的研究

数学开放题是一种条件和答案开放的数学问题形式. 它对训练、考查学生数学思维的灵活性和创造性有独特优势. 但传统的评价方式的低区分度等问题困扰着数学开放题的推广和应用. 研究者选择SOLO分类理论作为数学开放题编制、评分和解决能力评价的理论基础. 如依据SOLO分类理论对数学开放题评分［25-26］、通过SOLO层次与知识点数目的关系评价数学开放题难度［27］、基于SOLO分类理论的数学开放性问题评价系统建构的尝试［28］以及数学开放题认识水平的研究.

事实上，SOLO分类理论在开放题编制与评分方面是其应用强项. 通过设计符合该理论的数学开放题，分析答案的SOLO层次和设定有层次的评分标准，以便对学生的回答进行分类评价. 尽管数学开放题为思维方式和过程提供了更多空间，利用开放题的质化评价是未来数学评价的方向［29］，但现有研究主要是理论加案例的简单介绍居多，具有SOLO层次的数学开放题编制、题库建设、成熟的测试工具等深层次基础研究缺失.

（3）应用于数学问题提出能力的研究

随着数学教育对学生提出数学问题的重视，对问题提出能力的研究逐渐增多. 相关应用研究依据SOLO分类理论对学生问题回答的结果进行了水平划分，以此反映學生提出问题的能力. 如问题提出能力的研究［30］、教师课堂提问对学生问题解决能力影响因素的研究［31］、数学提问能力与认知方式的相关性研究［32］、问题提出能力与元认知的相关性研究［33］等. 实际上，数学问题提出能力与数学开放题编制、数学问题解决都有密切的联系，已有研究在以上方面均有涉及，无形中增加了研究难度，这很难保证在工具编制与测试评分方面的信效度.

（4）应用于数学中高考题的研究

数学中高考题的质量评价是数学教育评价领域关注的焦点. 可将SOLO分类理论应用于知识点和试卷层次结构作为第三方评价的理论基础. 如应用SOLO分类理论从知识点考查的视角来评价中高考数学试题，试图了解高考试题对相关知识点考查的力度［34］；依据SOLO理论制定符合高考要求的评分标准，将数学高考题划分为四个结构层次来考察试卷的能力结构和SOLO分布层次［35］；还有依据SOLO五个结构层次来考察数学中考试卷的难度［36］，考察中考试题的SOLO结构［37］. 上述研究成果为数学中高考题编制、评分、元分析提供了新视角，也为数学教学“以评促教、促学”提供了理论工具，对研究涉及的评分标准、工具的信效度要求较高.

（5）应用于数学课堂教学实践的研究

除上述数学认知水平、数学开放题、数学中高考题研究为数学教学提供指导外，具体的数学教学实践如数学教学设计、数学教学评价等，教师依据SOLO分类理论对教学目标、教学重难点和课堂提问等关键步骤进行了指导［38-39］. 同时在更具体方面，如学生数学解题能力［40］、变式训练［41］、教学评价［42］、数学日记评价［43］、作业评价［44］等也借助SOLO分类理论进行了研究.

数学教师对SOLO分类理论的应用已经超越以往单纯的“理论+数学教学案例”的介绍模式，更关注与实际教学活动紧密联系的教学评价活动，在某种程度上能切实扭转结果性评价的弊端，同时提升数学教学质量.

[?]讨论与建议

1. SOLO分类理论应用于国内数学教育研究的问题

上述的应用研究为SOLO分类理论在揭示数学学习心理、参与数学问题的编制与评分、指导数学课程教学等方面提供了理论基础，具有重大的理论和实践参考价值，但也暴露出了一些问题，主要表现在：

（1）研究广度有余、深度不足

文献梳理结果显示，已有的应用研究内容涉及数学内容多，研究对象和层次广. 以数学认识水平研究为例，涵盖小学、中学、大学主要数学内容，研究对象包括不同年龄段、学段的数学学习者. 但我们也看到，有部分研究虽集中于某一数学内容模块的认知现状，但都停留于划分数学学习者的认知水平，未能更进一步整合研究成果. 如对数学课程目标、教学目标从了解、理解、掌握等不同程度的精确划分上提供更加明确的研究支撑.

一线数学教师的研究虽然逐渐增多，但时有研究仅是基于经验积累对SOLO分类理论的尝试性应用，研究成果很有启发性但缺乏规范性. 如变式教学与SOLO分类理论相结合进行高效数学教学研究对数学教学“减负增效”很有参考价值. 但囿于研究者能力、研究方法和过程的规范性缺失而导致低层次研究较多.

在具体实施过程性评价时，依据SOLO理论对开放题的质化评价、学生课堂提问、数学日记等具体评价研究成果较多. 但依据SOLO分类理论编制的数学试题乃至相应题库的建设成果较少，这也是未来实施过程性评价应该努力的方向.

（2）对相关工具的信度和效度重视不够

在SOLO分类理论中对信度的关注焦点是交互判断的一致性，即不同研究者在评定同一回答时一致性如何［45］，这也会影响SOLO工具及其理论本身的信度. 基于SOLO理论的应用研究难点主要在各个水平判断方面，一般处理方法是多人评价. 许多研究并没有采取这一可能影响其评分信度的方式，研究结果未对此有专门讨论，无形中影响了研究质量. 效度指基于SOLO的测试结果与其他指标如学习成绩的相关性［46］. 尽管比格斯等人的研究结果显示SOLO与学生学习成绩相关，部分研究并没有通过类似指标检验研究结果的效度，研究完善度欠缺考虑. 总之，研究者对由SOLO分类理论编制的测试工具的信效度的探讨不够，一定程度上削弱了研究结果的影响力，可能阻碍学术成果的交流. 未来研究若能提升测量工具的信效度，有助于工具的成熟化和学术对话便捷.

2.对SOLO分类理论的应用研究的若干建议

（1）重视认知研究成果与基础数学课程、教学目标的整合

SOLO分类理论可为课程目标的设计、课程表现的等级评价等提供理论基础. 当前，我国基础数学课程目标和相对应的数学教学目标中的要求层次划分都存在泛化现象，具体教学实践指导乏力. 因此，依据SOLO分类理论划分数学认知水平之余应深入结合课程目标的不同层次明确不同层级的具体表现，课程目标清晰化、层次化是今后应用SOLO分类理论研究的重点.

（2）加强理论与数学教学实践相结合的行动研究

SOLO分类理论强大的生命力在于通过过程性评价切实改善教学实践、提升教学质量，这在已有的应用研究成果中有所体现. 如SOLO分类理论与变式教学相融合，对应对题海战术、提升学习效率大有裨益；在教学设计中可帮助教师明确教学目标、分析学生学情，能为例题、习题设计提供指导.

已有研究显示，与其他测量工具相比，SOLO分类理论更能深刻考查学生的能力，可在更广泛的层面被教师运用. 在数学教育评价很难摆脱重结果对错、唯分数论的纯量化模式下，SOLO分类理论评定数学学习结果时可定位学生学习的思维层次，更具有针对性地帮助教师发现教与学的问题，及时调整教学，敏感学生反馈，真正实现过程性评价功能.

3. 提升数学教学实践者应用SOLO分类理论的能力

SOLO分类理论的应用与研究者个人评价能力分不开. 广大教师是评價的主要力量，他们是否有能力和精力运用SOLO分类进行学生学习质量评价，在可操作性方面将面临挑战［47］. 如何根据学生回答的结果去判断和识别不同的结构也是技术性难题. 通过高校研究者与中学数学教师的合作研究帮助教师提升其理论应用水平是一种方式，同时在数学教师学习、培训等过程中提供学习SOLO分类理论的机会，以便增加和熟知相关知识，切实提升数学教师的理论应用能力.

综上所述，SOLO分类理论从一种学习结果评价工具成为一种揭示认识水平、指导测评题目编制和评分的工具，已经从单一的教育评价功能延伸至构建数学认知结构、指导高效课堂教学、改变教师的评价观和教学质量观等领域. 同时，从已有研究［48］推测，SOLO分类理论与其他测试工具和理论如PISA、TIMSS、APOS、范希尔理论等对数学学习认识过程的揭示可能出现某种类似对应. 这些多元理论能否在更高层次展开学术对话，能否在横向与纵向维度实现融合并应用于数学教育研究的诸多领域，也是未来研究可尝试的方向.

参考文献：

［1］［4］［45］［46］约翰 B.彼格斯，凯文 F.科利斯. 学习质量评价：SOLO分类理论（可观察的学习成果结构）［M］. 高凌飚，张洪岩，译. 北京：人民教育出版社，2010.

［2］赵利霞. 国内SOLO分类评价理论研究文献综述：1998-2008［J］. 江苏教育研究，2010（19）：10-14.

［3］冯翠典，高凌飚. 现状与反思：SOLO分类法国内应用研究十年［J］. 教育测量与评价，2009（11）：4-7+11.

［5］周超. 八年级学生数学认知水平的检测与相关分析［D］. 华东师范大学，2009.

［6］［47］刘京莉. 以SOLO分类为基础的学生学习质量评价初探［J］. 教育学报，2005（04）：41-45.

［7］李祥兆. 学生思维评价的新视角——SOLO分类评价理论评述［J］. 教育科学研究，2005（11）：20-22.

［8］蔡永红. SOLO分类理论及其在教学中的应用［J］. 教师教育研究，2006，18（01）：34-40.

［9］王传兵. SOLO分类评价理论及其在高中数学教学中的应用［J］. 中学数学教学，2007（04）：9-12.

［10］吴有昌. SOLO分类法在数学教学评价中的应用［J］. 中学数学教学，2011（04）：18-20.

［11］李俊. 学习概率中认知的发展［J］.数学教育学报，2002，11（04）：1-5.

［12］程龙海. 中学生数学解释的研究［D］. 华东师范大学，2003.