分设不同任务，体验方法多样性和多变性

周二伟

［摘 要］苏教版教材中“不规则物体体积的测量”这节课是要让学生“经过实践与探究，寻求解决问题的多种途径” 。教材只编排了“排水法”测量土豆体积的实验，教学时如果照本宣科，则方法单一，容易钳制学生的思想，制约学生的思维。文章给出了更多切实可行的测量方法，以增加实验操作的乐趣，增强学生学习数学的自信心。

［关键词］不规则物体体积的测量；排水法；多样性

［中图分类号］ G623.5［文献标识码］ A［文章编号］ 1007-9068（2022）32-0061-03

“不规则物体体积的测量”是苏教版教材第十一册的教学内容，教学目标是“经历测量土豆体积的过程，探究总结出测量不规则物体体积的基本原理和技巧”。教学这一部分内容，绕不开让学生亲手测量这一环节，而教材中测量土豆体积的方法过于单一，容易束缚学生的思维。测出结果不是终极目标，重点是让学生了解和掌握整个探究测量的过程，鼓励学生大胆创新、打破常规。因此，为了使实验更加接地气，充满生活气息，让更多切实可行、触手可及的测量方法走进学生的视野，同时增强实验操作的乐趣，笔者给学生提供了不同的测量任务，待测物品也是多种多样。

一、情境引入，抛出问题

教师首先利用多媒体给出一些生活物品的图片，有形状规则的（如长方体、正方体）、轮廓趋近标准的几何体，也有形状不规则的（如木雕、鹅卵石、橡皮、硬币、墨水瓶、肥皂、蚕豆和海绵等），然后提出问题：（1）上述物品中，哪些可以通过量得的尺寸直接计算体积？运用什么公式计算？（2）哪些物品无法通过相关数据直接测算体积？说出你的理由。

对于第（1）题，学生迅速说出只有形状为立方体的物品可以直接测算出体积，并脱口而出计算公式，正确无误。对于第（2）题，学生都支支吾吾地说“凹凸不平的”“表面不平滑的”“没有相关公式的”“不知道测量哪些数据的”等。面对学生的七嘴八舌，教师及时进行归纳总结，统一称之为“形状不规则的物体”，在教师的循循善诱下，学生纷纷追问：“如何计算不规则物体的体积呢？”

数学教学应“尊重学生的最近发展区，创设有利于学生自学的情境”。在本环节中，学生在抢答的氛围中积极展开思考，在教师的督导下，学生的好奇心被激发，自己提出问题“不规则物体该如何计算体积？”，为下一环节的教学开了个好头。

受先入为主的观念影响，学生在学习了规则几何体的体积公式后，就会形成思维定式，认为求物体的体积都是有计算公式的，这种观念越深，学生对体积概念的理解越是存在偏见，遇到不规则的物体，他们就会认为这些物体没有体积，这显然不符合体积概念的原始定义。不规则物体到底有没有体积？要说没有体积，它却确实占据了一定的空间大小；要说有体积，它却无法完美分割成若干个正方体的体积单位，那么“不規则物体的体积到底如何计算”就会成为萦绕在学生脑海中的一个谜题，在对这个谜题进行思考时，学生会自动重新审视和反思体积的概念。

二、任务各异，合作探究

1.组织讨论测量的方法

教师提出问题“既然没有现成的公式可以应用，那么能不能运用学过的技巧测量出不规则物体的体积呢？”后播放“乌鸦喝水”动画短视频。学生看完短视频后，先展开联想，然后分组研讨交流，最后集中汇报展示成果。

有了动画视频的启迪，学生各种新奇的想法喷涌而出，个个踊跃发言，主要分为两派：一派支持“升水法”，即把整个物体完全浸没在水中，盛水的容器必为长方体透明容器，容器中的水始终未溢出，测量物体浸水前后的水位高度差，用“容器的底面积×水位高度差”即可轻松求出浸水物体的体积大小。另一派支持“溢水法”，虽然还是要将物体浸入水中，但不同的是，容器中的水满至容器口，物品一旦浸没水中，容器中的水就会溢出，将排出的水倒入一个有刻度的量杯中，读取倒入的水的体积，这个体积即是浸没物体的体积。

令人赞赏的是，有的学生竟然使用逆向思维，反其道而行之，提倡用“降水法”，即先测量浸没物体后的水位高度，取出物体后，再次测量水位下降后的水位高度，算出两次测量的水位高度差，然后乘以容器底面积大小算出体积。此言一出，立马招来其他学生的质疑和反驳，理由是取出物体后，物体表面会沾上水，从而让取物后的水量减少，引起实验误差。最后，师生共同磋商并达成共识：“升水法”和“溢水法”都是运用“等积代换”的原理，即“不规则物体的体积=物体排开水的体积”。

2.分小组动手实验

教师将全班学生分成8个学习探究小组（每个小组分别从木雕、鹅卵石、木偶、硬币、肥皂、蚕豆和海绵中选择一样作为测量对象），并给出实验目标：

（1）规划好测量方案和详细步骤，再动手操作，小组成员要分工协作，全员参与，各司其职。

（2）容器中的水要适量，待测物体务必完全浸没水下，不得有半点露出水面。

（3）读数时，玻璃杯要放平，视线应与液面的凹面底部相平。

（4）同一物体要分别独立测量三次，测得的数据取平均值，如实地记录实验数据，填好实验记录单（如表1）。

（5）实验时要注意安全和卫生，非必要不得脱岗串岗，不许交头接耳、左顾右盼。

学生操作的方法五花八门，虽然每个小组只选择一种方法来实验，要么是“升水法”，要么是“溢水法”，但是具体做法各不相同。有的小组操作起来一帆风顺，有些小组阻碍重重。比如有一个小组选择的物品是木雕，由于浮力作用，木雕很难浸入水中；还有的小组测量结果误差很大，比如一个小组选择的待测物是肥皂，而肥皂会溶化在水中，从而导致测量结果有误差。教师要求各小组针对自己遇到的具体困难，自行寻找化解方法。经过一番冥思苦想，有的小组成功找到应对之策，有的小组还是一筹莫展。

3.活动交流与总结

在小组交流反馈过程中，学生归结出三大疑虑：第一，蚕豆和硬币体积都太小，浸入水里后看不出水位有什么明显变化，怎么测量？第二，木雕和海绵会浮在水面上，不靠外力很难稳定持久地浸入水中，如何化解？第三，肥皂容易溶解在水中，导致实验结果出现重大误差，怎么办？教师并没有直接给出答案，而是把“皮球”踢给学生。出人意料的是，学生居然想出一条条妙计：针对第一个物品体积小的难题，学生想出“聚集法”测量，比如多放一些硬币（如100枚）到水里，测出总体积，再计算出一枚硬币的“微体积”；对于第二、第三个问题，有的学生提议用面粉代替水，来个“偷梁换柱”，用“埋沙法”进行测量，以及在肥皂表面包裹一层保鲜膜……学生脑洞大开，灵感迸发，各种奇思妙想层出不穷。随后，教师对这些方法给予表扬和小结，重点解说“聚集法”和“埋沙法”的操作原理，并明确指出这些方法与“升水法”如出一辙，都是利用“等积代换”原理。最后，教师要求中途遇阻被迫终止实验的小组采取新办法继续实验，直至得出满意的结果。

在本环节中，学生经历了“发现疑难—寻找出路—制定方案—实践检验—交流反馈”的探究流程，尽管在实验的过程中发现客观存在的问题，但能够大胆质疑，通过独立思考、小组合作等形式寻找出路，寻求破局之道，形成综合运用知识的能力。

学生根据体积的原始定义——物体占据空间大小就是物体的体积，找到了测算不规则物体体积的有效途径，不规则物体的外表没有规则可言，无法形成固定的体积计算公式，但是，它又确确实实占据了空间，因此，可以将不规则的空间转化为规则的空间。将不规则物体的体积等量转化为规则物体的体积，这个转化过程必须依靠可流动的介质完成，而变化无穷的流体就成为首选，水就是没有固定形状的，但可以转化成任何形状，因此将不规则物体转化成等体积的水，然后装进规则容器里，就可以借助计算水的体积间接求出不规则物体的体积。

三、解题应用，拓展延伸

教师出示实验任务单，要求学生小组合作完成。

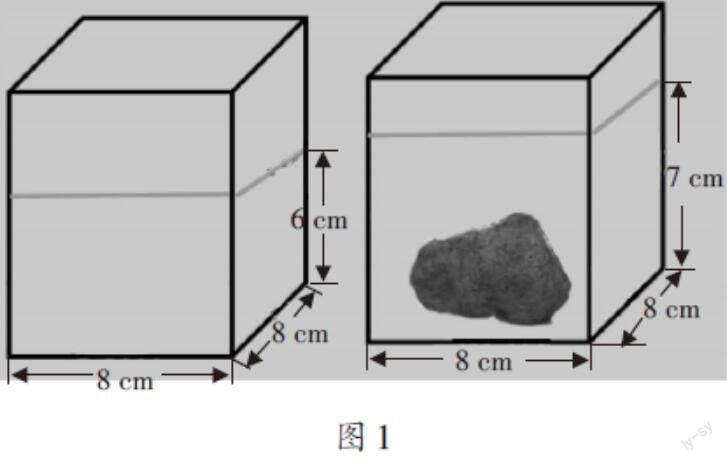
任务一：仔细看图1，说说石头的体积是多少。

任务二：一个圆柱体玻璃容器内有1.2升水，水面高15 cm，把一个番茄浸没水中，水位高变为16.5 cm，试着求出番茄的体积。

任务三：课外阅读“阿基米德鉴定皇冠”的故事，尝试揭示其中的道理。

任务四：说一说本节课学习了哪几种测量物体体积的方法？各种方法的操作流程是怎样的？

对于任务一，学生的完成情况十分可喜。对于任务二，许多学生清醒地意识到要事先求出容器的底面积，然后才能求出排开的水的体积，这是常规做法。也有学生另辟蹊径，如：前后水位高度差是1.5 cm，1.5 cm是15 cm的十分之一，因此番茄排开的水的体积应是原有體积的十分之一，也就是1.2升的十分之一，即0.12升，为120立方厘米。教师对该想法十分赞赏，鼓励学生积极探索简便巧妙的算法。任务三和任务四则是允许学生畅所欲言，各抒己见，教师及时点评。

设计实验任务单的主要目的有二：一是让学生巩固新知，学会运用；二是让学生尝试独立攻坚克难，独立应对问题。这些任务由学生先独立思考然后集体交流，目的是锻炼学生的组织能力和领导能力。

“排水法”是计算不规则物体体积的常用方法，但是教师在教学“排水法”的时候，往往浅尝辄止，只讲解物体完全浸没水中这一特殊情况：物体完全浸没在水中，水位升高，升高的水柱的体积等于物体的体积，而容器的底面积是已知的，这样就可以顺利求出升高水柱的体积。但是，如果物体刚好浸入水中，水面刚好将物体淹没，怎么计算体积？如果物体浸入水中后，水位升至容器口，还有部分水漫出容器外，那么此时的体积又该如何计算？这些都是平时教学中鲜有涉及的，而让学生尝试在不同的溢水情况下测算不规则物体的体积，可以加深学生对体积转化法的理解。

大多数教师教学这一课时，教了“排水法”就鸣金收兵，学生虽然懂得其中道理，也会做题，但是不会变通，也不知其中深意，一旦更换待测物，定会不知所措。因此，教师很有必要提供多种物品，让学生多体验几种测量方法。而采用每个小组完成不同任务的做法，避免了实验单调重复的弊端，极大地保护了学生的学习积极性，使学生在观察、思考、操作、计算、推理等一系列的探究过程中，大胆思考、大胆怀疑，感悟解决问题方法的多样性和丰富性，实现发现、分析和解决问题的连锁式反应，从而获取知识，提高数学思考力，让“做中问”“做中想”“做中学”的宏大目标得以实现。

［ 参 考 文 献 ］

[1] 章威维.如何更好地探索不规则物体体积的测量方法[J].小学数学教师，2021（Z1）：149.

[2] 方苏云.基于SOLO分类理论的数学理解能力测评与诊断：以“求不规则物体的体积”为例[J].小学数学教育，2021（05）：15-18.

[3] 李巍巍，孙铁.“巧求不规则物体的体积”教学实录与评析[J].小学数学教育，2020（Z1）：85-87.

[4] 郭勇.浅议游戏化学习的教学价值：以“不规则物体体积的测量”教学反思为例[J].小学教学研究，2018（29）：58-60.

（责编 金 铃）