紧扣价值悟特性 抓住关系来抽象

陈素华　冷满红

什么是数学？简单来说数学就是符号加逻辑。数学符号因其精确、严谨、可以参加运算等特征而具有自身的特殊性。如何引导学生经历符号的抽象过程，知道符号表达的现实意义，能够初步运用符号表示数量、关系和一般规律，感悟表达的结论具有一般性，并为过渡到代数式的运算、方程的教学等奠定基础？本文以“用字母表示数”第一课时的教学为例进行探讨。

一、在遵循历史中梯度推进，体会抽象必要性

从数学的发展历史来看，用字母表示数经历了漫长而曲折的过程，大致可以分为三个阶段：一是用算术算式表示数，二是用文字语句来表示数，三是用字母表示数。遵循这一历史进程，学生要从用自然数等表示数量多少的数字符号表达走向用字母表示一般数量与关系的概念符号表达。为了实现这一目标，一方面，需要唤醒学生算术表达的经验，在反复表达中引导学生反思，意识到算术表达的局限性；另一方面，需要让学生通过归纳推理，用已知推断未知，从而实现从具体走向一般。

为此，在引导学生用小棒摆三角形，并用算式表示所需要的小棒根数之后，教师可以引导学生思考：（1）你会用算式表示了吗？你还能继续写这样的算式吗？写得完吗？（2）你写的算式中，能否找到一个算式可以表示这里所有的情况？（3）观察一下你写的算式，什么变了，什么没变？（4）你能用一句话来描述三角形的个数与小棒根数之间的关系吗？这句话可以表示出这里所有的情况吗？（5）如果让你选，你会选择这些算术算式还是这句话来表示刚才的情况，为什么呢？（6）刚才的算式真的写不完吗？你能不能想想办法，用一个式子来表示所有的情况呢？（7）小棒的根数是用一个新的字母表示，还是用含有字母的式子表示更好呢？为什么？（8）这三种表达方式，如果让你选，你会选哪种呢？为什么？

在书写算术算式的活动中，学生一方面适应用一个算式表示结果（小棒的总根数），一方面积累一定数量的算式为后续经过归纳推理，抽象得出一般结论提供探究素材。对书写过程的反思，促使学生意识到：这样的算术算式有无数个，这些算术算式都有相同的结构，即都是用三角形的个数乘3；在这些算式中，任何一个单独的算式都不能表示所有的情况。活动中，不断变化的数量为抽象成用字母或含有字母的式子表示数提供了必要性，不变的数量关系为学生经历由抽象走向一般的过程提供门径。

这样的教学过程，与数学史上有关符号抽象的发展历程基本吻合，體现了知识的“再发现”过程。学生在梯度推进中感悟用字母表示数的概括性、简洁性特点，体会到抽象的必要性与进行抽象的基本方法。

二、在变与不变中聚焦关系，感悟抽象关键点

从学生的数学现实来看，在本课之前，学生已具备用字母表示数的一些经验。与旧知对比，本课学习的难点应是从用符号表示单个数量，走向用“字母式”表示相关数量与数量关系。要突破其中的难点，完成抽象过程，需要继续引导学生学会抓住“关系”来表达。为此，可以设置如下教学环节。

结合线段图出示：甲、乙两地之间的公路长280千米，一辆汽车从甲地开往乙地。然后引导学生思考交流：（1）汽车可能在哪个位置？已行的路程是哪一段？未行的呢？（2）不管汽车在哪个位置，什么数量不会发生变化？（3）如果汽车已经行驶了50千米，剩下的路程是多少？你会用算式来表示吗？如果已行了74.5千米呢？200千米呢？（4）在刚才所写的算式中，什么变了，什么不变？这样的算式写得完吗？（5）已行的路程有多少种情况，该怎么表示，用字母a表示可以吗？用字母b表示可以吗？（6）剩下的路程该怎么表示，用字母c来表示可以吗？280-a与c相比，在表示剩下的路程上，有什么优势呢？（7）在这个式子中，字母a表示的数量最小是多少？最大呢？

从线段图的直观感知——在变化之中寻找关系，奠定抽象的具象基础；到用数字符号计算——在计算中体会关系，丰富抽象的运算经验；到用概念符号来表达——在概括中书写关系，用符号表达抽象结果。在这个教学过程中，教师始终围绕着不变的数量关系来做文章，为学生从具象到抽象提供了思考问题的视角与思路，使其感悟抽象关键点，积累数学抽象的活动经验。

三、在分层练习中逐步进阶，提升抽象表达能力

抽象的主要对象是现实生活中的数量与数量关系、图形与图形关系，抽象形成了数学的研究对象，并用定义或符号加以表达。面对具体情境中的数量关系，学生能否正确运用符号进行表达，是学生抽象水平的外在表现。如果说前面的教学实现了对抽象特点的感悟与表达门径的理解，那么接下来的练习环节则应带领学生具体运用符号表示数量、关系和规律，从而形成表达的一般策略。

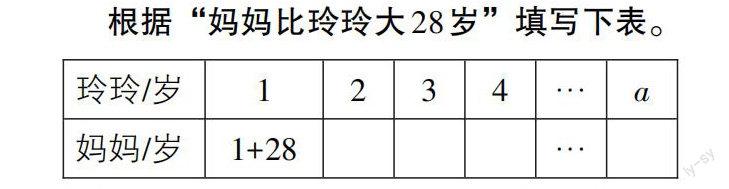
1. 基本练习——直面本课知识内核。

学生独立完成后，展开师生交流：表格中什么在变，什么不变？问题引导直指本课教学的核心内容——抓住关系来表达，帮助学生形成基本技能。

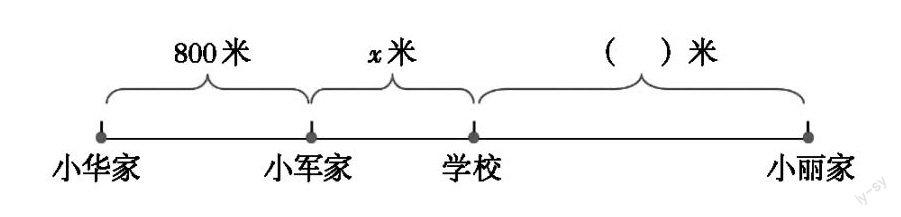
2. 变式练习——构造矛盾，完善结构。

在练习中，教师适时引导学生思考：x米表示的是哪段路程？小丽家到学校的路程可不可以用x米或者含有x的式子来表示？如果知道小丽家到学校的路程比小军家到学校的路程多300米呢？“800+x+y”表示的是从哪里到哪里的路程？一系列的追问，引领学生深度感悟用字母表示单独数量与用字母式表示相关数量的不同，在辨析中提升符号表达的能力。

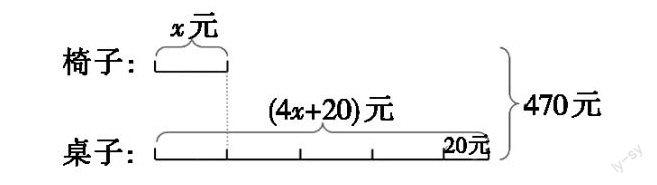
3. 拓展练习——变化关系，体会不同。

（1）出示：椅子的价格线段、桌子的价格线段。提问：这里椅子的价格是未知数，该怎么表示？桌子的价格呢？ （2）将桌子的价格线段均分为四等份，且每份和椅子的价格相等。接着引导思考：桌子的价格现在你还想用y来表示吗？为什么？ （3）桌子的价格再增加20元。提问：现在还能用4x来表示吗？该如何表示呢？（4）增加条件：一共470元。提问：你能用一个等式来表示这道题中的数量关系吗？

四个问题，指向抽象的不同层次，从表示没有关系的两个数量，到有关系的数量表达，到最后用“方程”表示等量关系，在逐层进阶中提升学生的抽象表达能力。

（作者单位：安徽省潜山市余井中心学校 江苏省苏州市相城第一实验小学）