运算教学中的数学语言转换

李海东

摘 要：培养小學生的运算能力是教师的重要教学任务之一。数学语言转换能有效帮助学生明晰运算对象、理解运算算理、掌握运算方法、发展推理能力，促进学生发展和提升数学运算能力。

关键词：运算教学；运算能力；数学语言转换

在小学数学教学中，培养学生的运算能力是教师的重要教学任务之一。《义务教育数学课程标准（2022年版）》指出：“运算能力主要是指能够根据法则和运算律进行正确运算的能力。能够明晰运算的对象，理解算法与算理之间的关系；能够理解运算的问题，选择合理简洁的运算策略解决问题；能够通过运算促进数学推理能力的发展，形成规范化思考问题的品质，养成一丝不苟、严谨求实的科学态度。”数学教学也就是数学语言的教学。因此，数学运算教学离不开数学语言转换。在有效的数学语言转换中，学生可以明晰运算对象、理解法理关系、选择运算策略、发展推理能力、规范思考品质……教师要引导学生正确、迅速地进行数学语言转换，才能有效培养学生的运算能力，提升学生的数学运算水平。

一、阅读中转换，明晰运算对象

阅读是学生用数学眼光观察世界的有效方法之一，也是学生获取数学信息的基础，更是学生形成运算能力的前提。有效的数学阅读有助于学生明晰运算对象。教师要引导学生在阅读中了解运算信息，并在去伪存真、由表及里中准确把握运算对象的本质。有时，学生对运算对象的内涵、名称等未必熟悉或理解。教师要鼓励学生积极思考，努力对关键信息进行数学语言转换，尽量用自己熟悉或容易理解的数学语言表述运算对象，为正确运算做好充分准备。

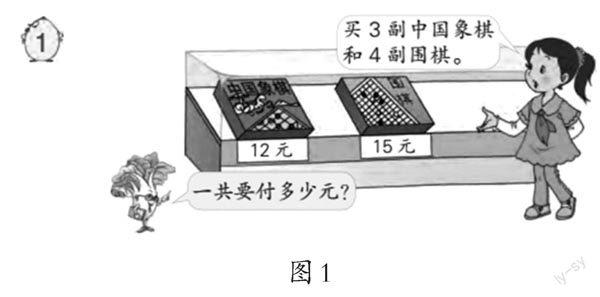
比如，苏教版数学教材四年级下册“整数四则混合运算”例1的情境图（如图1）。

学生仔细观察情境图，很容易发现一些数学信息：买一副中国象棋要12元，买一副围棋要15元，买了3副中国象棋和4副围棋。问题是一共要付多少元。要求购买中国象棋和围棋两种棋的总费用，需要先求出买两种棋各用多少元，再把这两种数相加。可以分步列式，也可以列综合算式解决问题。这是在三年级学习两步运算的基础上学习的新知识。区别在于三年级只要先求一种商品的费用，这里要先求两种商品的费用。

明晰运算对象就是要弄清题意，知道题目想干什么。能否明晰运算对象的本质是学生数学阅读水平的重要标志，也是培养学生运算能力的前提条件之一。通过数学阅读，学生可以把生活问题数学化，情境图可以逐渐抽象为3个12元和4个15元的和是多少。明晰运算对象的过程就是把图形语言（情境图）转换为文字语言的过程。这样转换，学生就能整体认识运算对象，弄清题意，把握知识本质。准确进行数学语言转换，为学生有效地理解运算对象奠定了基础。

二、探究中转换，理解算理与算法关系

引导学生理解算理、掌握算法是培养学生运算能力的关键：算法能帮助学生解决“怎样算”的问题，算理能帮助学生解决“为什么要这样算”的问题。算理和算法都需要学生在运算教学过程中独立探究和自主发现。苏教版小学数学教材一般不直接揭示运算方法，而是通过一些提示语，如“在小组里说一说，乘法可以怎样算？”，引导学生在探索和交流中逐步抽象、概括运算法则。因此，教师要“设计必要的数学活动，让学生通过观察、实验、猜测、推理、交流、反思等，感悟知识的形成和应用。”经历探究活动过程时，教师要引导学生在数学语言转换过程中正确理解算理与算法的关系，帮助学生逐步形成运算技能。

教学苏教版数学教材六年级上册“分数乘法”时，教师出示例题（如图2）。

做一朵绸花要用[310]米绸带。

1.小芳做3朵这样的绸花，一共用绸带几分之几米？

2.小华做5朵这样的绸花，一共用绸带几分之几米？

解决问题1时，学生可以列加法算式[310]+[310]+[310]，或乘法算式[310]×3。从图中学生可以看出3个[310]是[910]米，即[310]×3=[910]米，也可以根据加法算式求出[310]+[310]+[310]=[3+3+310]=[910]米。因此，[310]×3=[310]+[310]+[310]=[3+3+310]=[910]米。

教师追问学生：“[3+3+310]为什么等于[910]？”有的学生认为[310]+[310]+[310]=[3+3+310]=[3×310]=[910]米，有的学生认为[310]×3表示3个[110]×3就是9个[110]，也就是[910]米。学生从中不但能了解分数乘整数的算理，而且能初步感知分数乘整数的运算方法。

解决问题2时，个别学生列加法算式[310+][310+310+310+310]，多数学生列乘法算式[310]×5，并根据刚积累的经验，类比出[310]×5=[3×510]=[1510]=[32]米，知道[310]×5表示3个[110]×5，就是15个[110]，也就是[1510]，即[32]米。学生在独立思考和小组交流中理解了分数乘整数的算理，并归纳出运算法则——分数和整数相乘，用分子和整数相乘的积做分子，分母不变。

分数乘整数的算理和算法对学生而言都很抽象。教师要引导学生借助直观图理解算理、探究算法。学生把同分母分数加法的算理和算法顺利迁移到分数乘整数的运算过程中，知道了[310]×3为什么可以写成[3×310]。根据题意列式并求出结果的过程是学生把图文结合的图形语言（情境图）转换为符号语言（算式）的过程，讲算理、说算法是把符号语言转换为自然语言，最终用文字语言概括出运算法则。学生不但需要借助直观图经历探索和感悟过程探究算法，而且需要根据算法进一步理解算理。在有效的数学语言转换中，学生能主动、积极地经历运算法则的形成过程，从而在经历“分数乘整数”知识的“再创造”过程中逐渐理解算理、掌握算法，并沟通两者之间的关系，在“法”“理”和谐中“知其然且知其所以然”。

三、理解中转换，选择运算策略

理解运算问题就是要弄清楚运算教学的目的和问题的本质。正确理解运算问题，学生才能确定合理的运算思路，才能选择正确、合理、简洁的运算策略去解决问题。运算策略的选择决定了学生解决运算问题的过程是否高效快捷，体现了学生自身运算水平。如果选择的运算策略比较简洁，学生的运算过程就会比较简洁，运算速度就会比较快；反之，学生的运算过程就会比较繁杂，就会事倍功半。在理解运算问题的过程中，学生需要不断进行数学语言转换。学生理解运算问题越深刻，数学语言转换就越迅速，选择的运算策略就会越简洁、越合理。

比如，苏教版小学数学教材五年级下册“解决问题的策略”的例2是求[12]+[14]+[18]+[116]。很多学生会按照从左往右的顺序依次通分相加，即[12]+[14]+[18]+[116]=[34]+[18]+[116]=[78]+[116]=[1516]；也有的学生会一次性通分，即[12]+[14]+[18]+[116]=[816]+[416]+[216]+[116]=[1516]。两种运算方法无疑都是正确的，但比较麻烦，而且反映了学生没有真正理解运算问题。因为教材的设计是希望学生通过转化策略迅速、简洁地解决问题。学生只有能正确理解运算问题，才有可能想到转化的策略，才能联想到“分数意义”中把一个圆、一个正方形或一个线段看作单位“1”的知识，才会想到用转化的策略画图（如图3）解决问题，即[12]+[14]+[18]+[116]=1-[116]=[1516]。

无论是整数、小数还是分数四则混合运算教学中，教师只有引导学生正确理解运算思路，并且关注学生的差异化运算思路，才能启发诱导学生想到用不同的运算策略去解决相同的运算问题，才能引导学生优化运算策略，才能提高学生的运算速度和运算能力。如果学生想不到转化策略，教师可以引导学生思考例1中的不规则图形是怎样进行比较的，学生就会想到转化策略，就会联想到分数意义中的单位“1”。学生理解运算问题的过程要把符号语言转换为文字语言，选择运算策略的过程要把符号语言转换为新的符号语言或图形语言。通过有效转换，学生才能正确选择运算策略，才能使解决问题的策略更简洁、更合理。

四、推理中转换，形成运算品质

思维品质是学生思维的个性特征，反映了学生个体智力或思维水平的差异，主要包括思维的深刻性、思维的灵活性、思维的独创性、思维的敏捷性和思维的批判性。运算能力和推理意识是小学生数学思维的主要表现。运算教学中的推理主要以归纳或演绎的方式存在，具有一定的严密性和逻辑性，这种严密的逻辑思维就包括分析能力、类比归纳能力、推理论证能力、抽象概括能力等。在运算教学中，教师虽然不要求学生具体说出自己是如何进行推理的，但学生说算理或运算程序的过程包含了数学推理。当然，学生在推理过程中需要不断进行数学语言转换。教师要恰当引导，促进学生在推理中形成良好的运算品质。

学生探究规律的过程往往要经历归纳推理的过程。教学“加法交换律”时，教师先引导学生根据情境图（如图4）中的跳绳问题，列式28+17=45或17+28=45，得出28+17=17+28后，再寫出几个类似的例子，如1+2=2+1，123+321=321+123等，再引导学生在观察中归纳出算式中蕴含的规律——两个数相加，交换加数的位置和不变，也有的学生用甲数+乙数=乙数+甲数、○+□=□+○、?+◎=◎+?……表示规律，最后引导学生抽象概括出用字母表达的加法交换律——a+b=b+a。学生归纳加法交换律的过程中多次进行了数学语言转换：分析情境图，要把图形语言转换为符号语言（算式）；把算式中蕴含的规律用文字语言或符号语言表述出来，要把符号语言转换为文字语言或新的符号语言；把规律用a+b=b+a表达，就统一转换为符号语言了。引导学生迅速归纳概括规律，能有效培养学生的思维敏捷性；鼓励学生用不同形式表达规律，能有效培养学生的思维独创性……

竖式计算和简便运算过程中蕴含了演绎推理，也是培养学生良好的数学思维品质的有效途径。在简便运算3.2×1.25时，只要教师能充分提供思考时间和空间，学生会出现很多不同的方法：用乘法分配律包括3.2×1.25=（4－0.8）×1.25=4×1.25－0.8×1.25=5-1=4或3.2×1.25=（3+0.2）×1.25=3×1.25+0.2×1.25=3.75+0.25=4；用乘法交换律和结合律包括3.2×1.25=4×0.8×1.25=（4×1.25）×0.8=5×0.8=4或3.2×1.25=0.4×8×1.25=0.4×（8×1.25）=0.4×10=4等。无论哪种方法的运算过程中都蕴含了演绎推理。用乘法交换律和结合律进行简便运算的推理过程如下：大前提是乘法交换律和结合律，小前提是3.2=0.4×8或3.2=0.8×4，结论是3.2×1.25=（4×1.25）×0.8=5×0.8或3.2×1.25=0.4×8×1.25=0.4×（8×1.25）=0.4×10。学生在演绎推理中多次进行了数学语言转换：递等式是把符号语言转换成新的符号语言，交流不同的运算思路或运算方法要把符号语言转换为文字语言。鼓励学生用不同方法进行简便运算，能有效培养学生思维的灵活性、独创性和深刻性，学生只有对运算律有深刻认识，灵活运用运算律，才能想出不同方法，甚至想到比较独特的运算方法；鼓励学生把自己的思路表达出来，能有效促进学生进行严密的推理论证，从而促进学生规范化思考问题，帮助学生养成一丝不苟、严谨求实的科学态度。

总之，在数学运算教学中，教师要引导学生学会“用数学的眼光观察现实世界、用数学的思维思考现实世界、用数学的语言表达现实世界”，以便学生在运算中明晰运算对象，理解运算“法”“理”，选择运算策略，形成思维品质，从而有效培养和发展数学运算能力。当然，培养小学生的运算能力不是一蹴而就的事，需要教师在长期的运算教学中持之以恒地进行引导，促进学生逐步养成从数学角度观察现实世界的意识与习惯，逐步养成讲道理、有条理的思维习惯和理性精神。有效的数学语言转换是培养和发展学生运算能力的有效保障。

（作者单位：江苏省泰兴市南沙小学）

参考文献

[1]中华人民共和国教育部.义务教育数学课程标准（2022年版）[S].北京：北京师范大学出版社，2022：8.

[2]中华人民共和国教育部.义务教育数学课程标准（2011年版）[S].北京：北京师范大学出版社，2012：63-64.

[3]刘晓萍.素养立意下小学运算教学的价值与策略[J].课程教学研究，2019（9）：35-40.