AP1000安全壳在大型商用飞机撞击下的动力响应分析

汪大洋， 汪秀清， 杨 强， 张永山， 吴成清

(1. 广州大学 土木工程学院，广州 510006; 2. 悉尼科技大学 土木与环境工程学院，悉尼 2007)

核能作为一种清洁且高效的重要能源，已经成为电力工业发展一种必然趋势。然而，随着恐怖袭击的日益猖獗和现役飞机数量的迅速增加，核电厂正面临越来越多的蓄意和意外飞机撞击威胁。特别是“9·11”事件以来，大型商用飞机对核电站的撞击成为关注焦点，我国国家核安全局发布HAF 102—2016《核动力厂设计安全规定》[1]明确要求核电站考虑商用飞机恶意撞击。核电安全壳是核燃料反应堆最后一道安全屏障，其重要性不言而喻。

在试验研究方面，1993年美国Sandia国家实验室同日本Kobori研究所联合进行F4“鬼怪式”战斗机原型撞击钢筋混凝土厚板试验[2-4]，得到飞机冲击平面靶板的撞击力时程曲线，将其同利用Riera模型的理论计算结果进行对比，验证了Riera模型的正确性，该试验也是全球目前唯一一个足尺模型试验。孔建伟等[5]将CPR1000核电站安全壳作为研究对象，设计了1/20安全壳模型，采用16 kg混凝土块模拟质量为13 t的新舟600客机，用质量为140 kg的铁制圆筒模拟质量为40 t的波音737-800客机，研究了飞机模型撞击下安全壳结构的动力响应和损伤破坏现象及其过程。

在仿真研究方面，左家红等[6-7]采用ADINA软件对秦山核电站进行了动力响应分析研究，讨论了安全壳撞击区域的非线性行为。Kukreja[8]对PHWR核电站的双层安全壳进行了简化非耦合数值模拟，结果表明该安全壳有足够的承载能力来抵御B707-320和A300B4-200飞机撞击。Iqbal等[9]和Sadique等[10]采用ABAQUS软件建立了1.2 m厚钢筋混凝土安全壳有限元模型，分别将5种不同飞机的撞击荷载时程曲线直接加载到安全壳结构上，研究分析了结构的动力响应。曹健伟等[11-14]建立了新舟MA600飞机、空客A320飞机和预应力钢束钢筋混凝土安全壳有限元模型，开展了耦合与非耦合有限元仿真研究。本文课题组针对AP1000核电站结构的地震动性能展开了相关研究[15-18]，对其安全壳结构及其力学性能有较深入理解。

由于试验复杂、费用巨大，试验研究难以对大型商用飞机撞击下的核安全壳的整体动力响应进行详细分析。随着有限元快速发展，数值模拟成为一条重要研究途径，并取得了较多的成果。本文以波音737 MAX 8大型商用飞机和AP1000安全壳为研究对象，进行安全壳在不同初始撞击速度和撞击高度下的动力响应分析，研究安全壳的损伤破坏机理，其结果可为后续安全评估和结构设计提供参考。

1 有限元模型

1.1 AP1000安全壳

根据西屋电气公司关于AP1000的设计文件和团队现有AP1000安全壳结构[19]进行建模，AP1000安全壳是一个自由直立的圆柱形钢制容器，带有椭球形的上封头和下封头。钢制安全壳容器被完全包容在一个混凝土屏蔽体中。直径39.62 m，总高度65.63 m，其中圆柱形筒壁高度54.16 m(地下部分为12 m)，圆形穹顶高度11.47 m。圆柱形筒壁钢板厚度44.45 mm，圆顶钢板厚度41.27 mm，如图1所示。

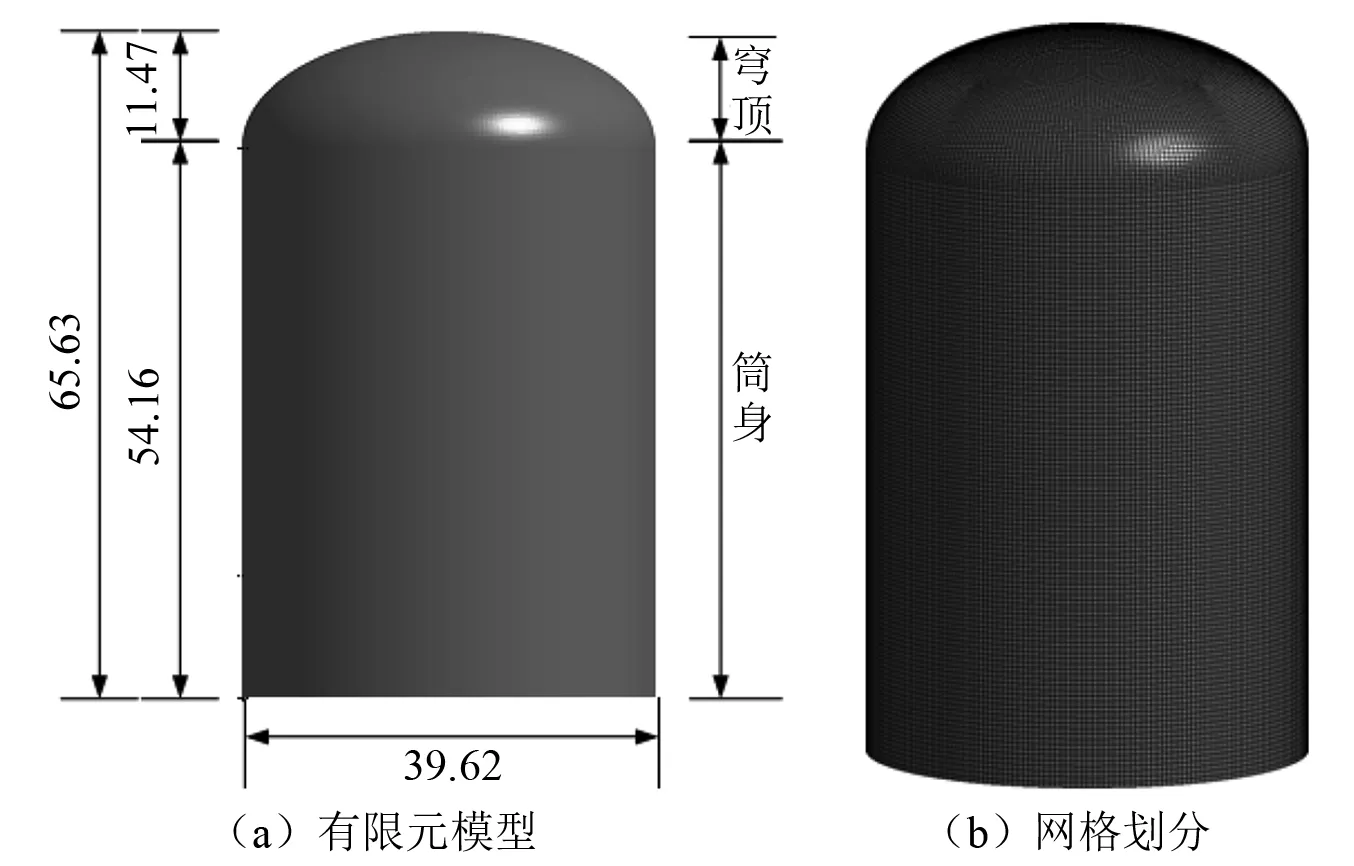
图1 安全壳有限元模型及网格划分(m)Fig.1 Finite element model of containment and meshing(m)

采用壳单元(SHELL163)仿真建模，单元厚度为结构各部分实际厚度。单元尺寸统一500 mm×500 mm，单元总数55 808。钢制安全壳SA738-B型钢材，密度7 870 kg/m3，弹性模量2.0×105MPa，泊松比0.2，屈服应力415 MPa，切线模量1.0×103MPa[20-21]。钢材本构模型选用*MAT_PLASTIC_KINEMATIC，在关键字文件中打开应变率。在飞机撞击安全壳过程中使用*CONTACT_AUTOMATIC_NODES_TO_SURFACE模拟飞机机身、机翼和引擎部件与安全壳之间的接触，罚函数系数取1.0确保合理接触。通过关键字文件*HOURGLASS在不同部件(*PART)上执行沙漏控制。

1.2 波音737 MAX 8飞机

波音 737 MAX 8[22]总质量约80 t，其中两台引擎质量约10 t。总长度约39 m，翼展长度约36 m，机身直径约3.88 m，如图2和图3所示。由于文件资料有限，故现根据已经掌握的设计文件资料对飞机模型进行简化：①几何形状与实际飞机相同；②考虑飞机蒙皮等主要结构，包括机身、机翼和引擎，所有尺寸均与实际相同，未考虑飞机内部连接和构造；③仅建立飞机结构模型，未考虑飞机燃料、货物和乘员状况。

采用壳单元(SHELL163)对飞机建模，采用MATLAB软件计算飞机几何模型机身、机翼及引擎的面积，再根据飞机材料密度，求得机身壳单元厚度约为32 mm，左右大翼壳单元厚度约为36 mm，引擎壳单元厚度取19 mm。Boeing 737 MAX 8飞机引擎为超级钢材料，机身与机翼为铝合金材料。飞机材料本构模型均采用*MAT_PLASTIC_KINEMATIC，考虑了材料失效、塑性流动，模拟金属材料在撞击过程中的动力响应，其具体的材料参数如表1所示。根据文献[23-24]对材料失效应变分析，确定机身铝合金材料的失效应变为0.05，机翼铝合金为0.01，引擎超级钢为0.1。单元尺寸统一为500 mm×500 mm，单元总数3 459个，其中铝合金材料单元个数3 075，超级钢384个。飞机各部件之间采用共节点处理。

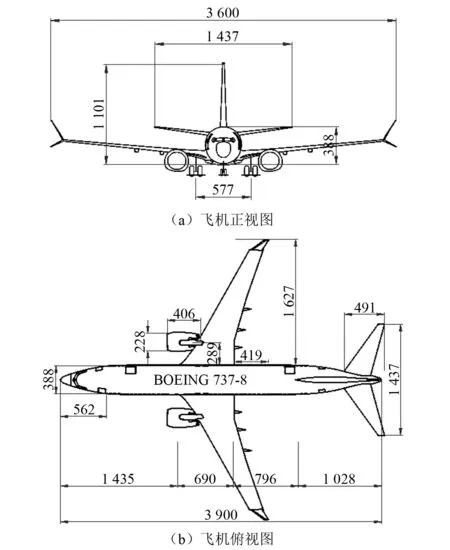
图2 波音737外形及几何尺寸(cm)Fig.2 Shape and geometric of Boeing 737 (cm)

图3 波音737 MAX 8Fig.3 Boeing 737 MAX 8

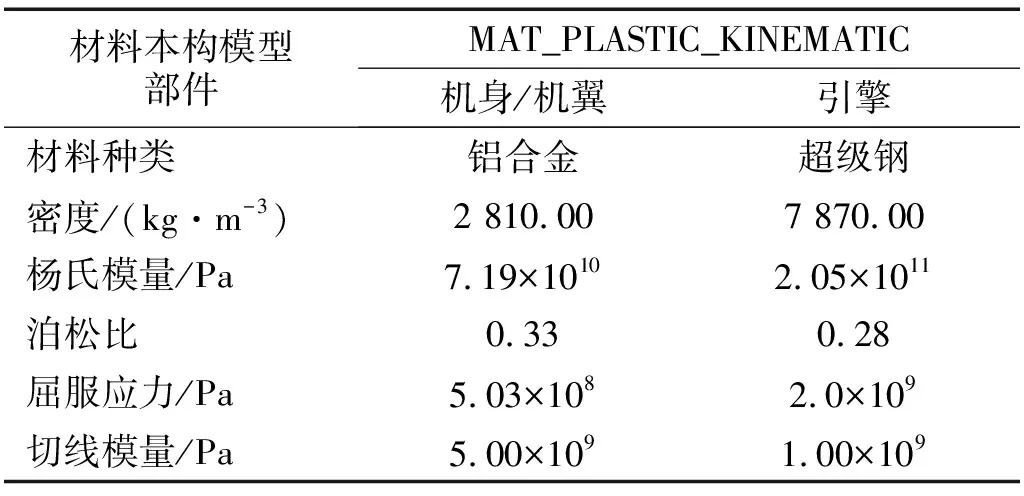
表1 飞机材料参数Tab.1 Aircraft material parameters

2 基于Riera法的飞机模型验证

首先通过Riera法计算得到大型商用飞机波音737 MAX 8撞击刚性墙的撞击力时程曲线和冲量时程曲线，然后利用ANSYS/LS-DYNA建立飞机和刚性墙模型并进行撞击过程仿真，最后对比分析撞击力的理论数值模拟结果来验证飞机有限元模型的准确性。

2.1 Riera法计算撞击力

设t=0开始撞击刚性墙，在t时刻速度为V(t)，质量为M(t)，机头到压碎位置距离X(t)，飞机质量密度μ[X(t)]。由动量定理可得撞击力F(t)计算公式

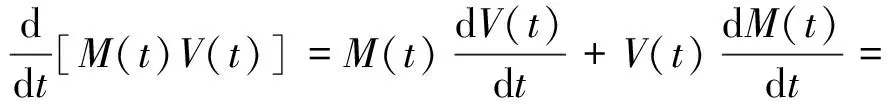
(1)

假设Pc(X)为飞机压碎力，在撞击处由于假定飞机材料为刚塑性，因此撞击处材料一维杆内力为Pc(X)，并对未撞碎区域取隔离体，由牛顿第二定律可得

Pc(X)=M(t)a(t)

(2)

因此Riera法可写成

P(t)=Pc[X(t)]+μ[X(t)]V2(t)

(3)

式中：P(t)飞机总撞击力；Pc[X(t)]飞机在该位置压碎力；μ[X(t)]飞机单位长度质量，不考虑撞击过程质量损失；V(t)飞机未压碎部分剩余速度。

根据文献[25]，飞机初始撞击速度取200 m/s，μ为1。Riera法理论计算出的撞击力曲线，如图4所示。

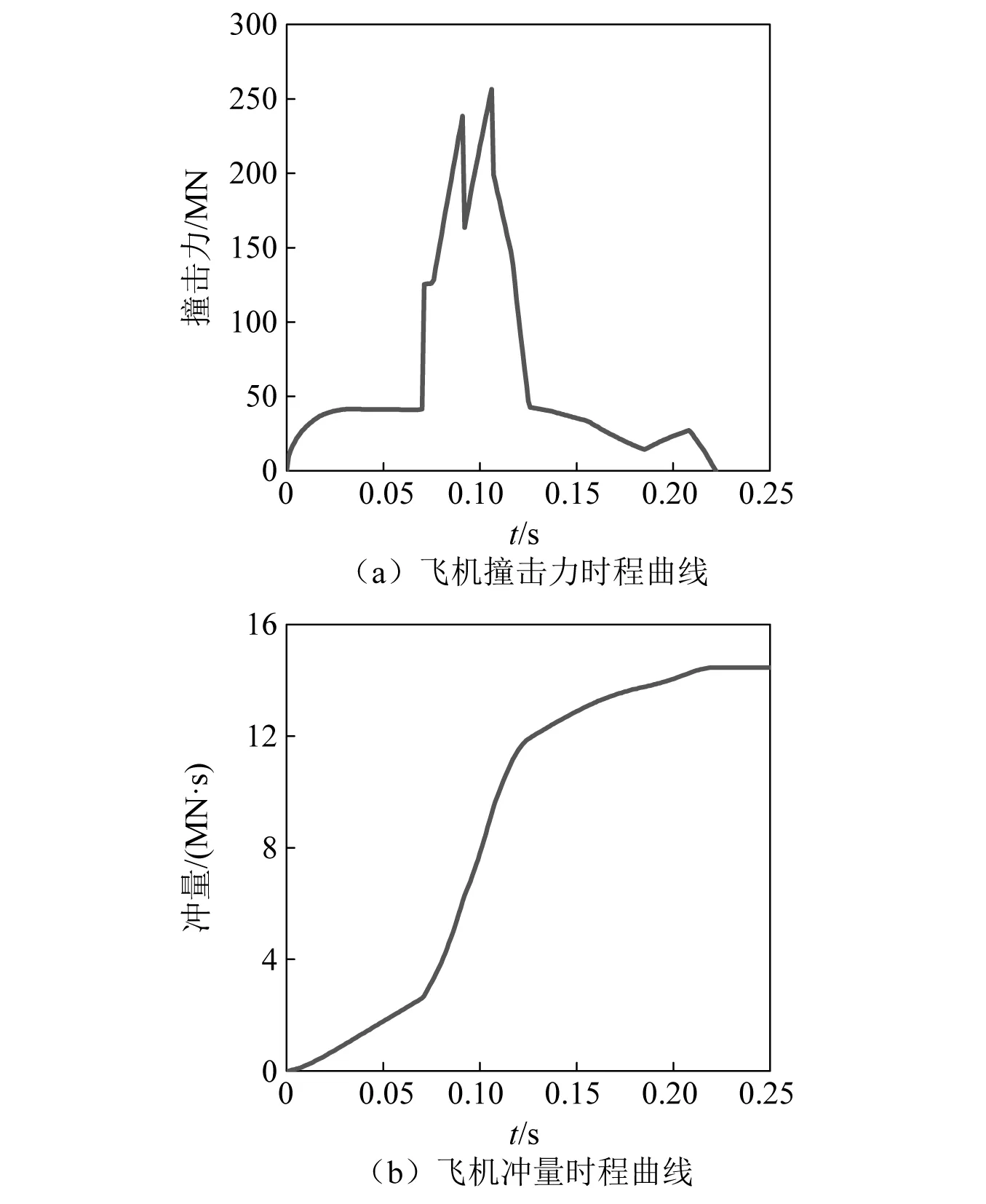
图4 Riera法理论计算结果Fig.4 Theoretical calculation result of Riera

2.2 基于Riera法的飞机模型验证

飞机初始撞击速度200 m/s，飞机垂直撞击刚性墙。有限元模型如图5所示，在墙体中心位置进行撞击，考虑飞机翼展长度和撞击区域的长度，墙体长度和宽度均取50 m，厚3.5 m，墙体四周固定约束。采用实体单元SOLID164建模。在墙体长和宽度方向上，单元尺寸取500 mm，厚度方向等分10份。墙体为素混凝土，在ANSYS/LS-DYNA软件中采用关键字文件*DEFORMABLE_TO_RIGID将墙体定义为刚性墙。

图5 飞机撞击刚性墙有限元模型(m)Fig.5 Finite element model of impacting the rigid wall(m)

Riera法理论和仿真结果对比，如图6所示。对比分析可得，两者的飞机撞击力时程曲线和冲量时程曲线的趋势基本一致，且飞机撞击力峰值最大误差为1.11%，飞机冲量最大误差为3.73%。可知，所建模型和相关参数设计是合理的，可以用于后续分析。

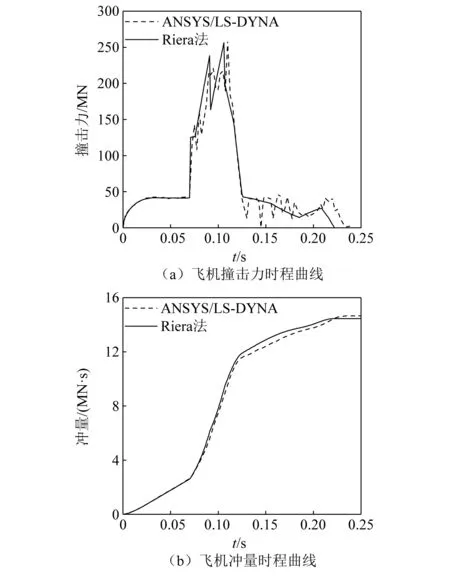
图6 Riera法理论计算结果与数值模拟结果比较Fig.6 Results comparison between Riera’s theoretical calculation and numerical simulation

3 撞击计算结果及分析

根据目前民航飞机在起飞和着陆的所有速度及现有飞机坠毁记录，飞行速度约100 m/s。波音737 MAX 8巡航速度约233 m/s。考虑到飞机坠毁、劫机或恐怖袭击时的蓄意撞击，将飞机初始撞击速度设为100 m/s，150 m/s，200 m/s，250 m/s和300 m/s。同时为研究撞击高度对安全壳动力响应的影响，撞击高度设为P1(30 m)、P2(39 m)、P3(47 m)、P4(54 m)、P5(65 m)，其中：P1(30 m)和P3(47 m)分别为钢安全壳内部等效钢梁筒身处，P2(39 m)为两个等效钢梁之间的非等效钢梁筒身处，P4(54 m)为安全壳筒身与穹顶交界处，P5(65 m)为安全壳穹顶位置，如图7所示。飞机撞击工况表如表2所示。撞击全过程分4个阶段：第一阶段，机头和前部机身；第二阶段，中部机身、引擎和机翼；第三阶段，中部机身和机翼；第四阶段，后部机身和尾翼。依次定义为T1、T2、T3、T4，同时将撞击末时刻定义为T5。为节省计算时间，仅考虑计算单侧撞击面的撞击作用，由于撞击速度不同，飞机撞击单侧面的作用时间依次定义为0.40 s，0.35 s，0.25 s,0.20 s,0.15 s。

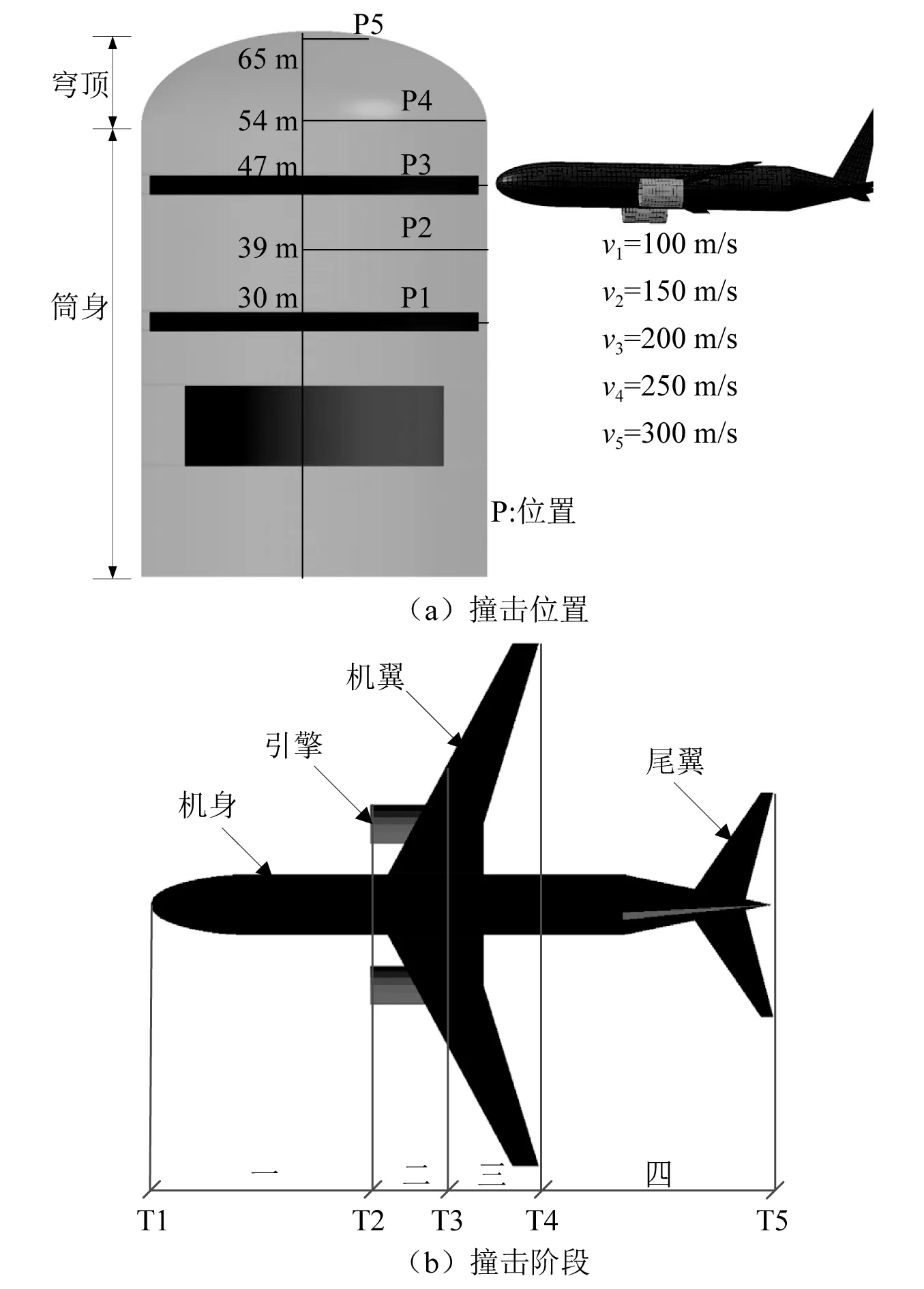
图7 撞击位置及撞击阶段示意图Fig.7 Diagram of impact position and impact stage

表2 工况表Tab.2 Investigation cases

3.1 飞机动力响应分析

3.1.1 飞机撞击破坏现象

由图8(a)可以看出P3V1工况中的飞机撞击破坏现象。在t=0.08 s时，飞机机头撞击到安全壳压屈破坏，后面的主要机身以及引擎和机翼未发生明显的变形，机身未进入安全壳内部；在t=0.16 s时，飞机引擎撞击到安全壳，机身后面的部位未发生明显的变形，飞机机身亦未进入安全壳内部；在t=0.24 s时，飞机的进一步破坏，引擎变形加大且已与机翼分离，靠近机身的机翼根部已经完全压屈破坏，飞机机身未进入安全壳内部；在t=0.32 s时，飞机剩余的机身未进一步破坏，但靠近机身的机翼根部已经完全破坏，飞机机翼尾的尾部发生断裂飞出，分布在安全壳两侧，引擎破坏情况没有明显加剧，但是其发生翻转，剩余飞机机身未进入安全壳内部；在t=0.40 s时，飞机剩余的机身仍未进一步发生破坏且未进入安全壳内部，剩余的引擎和机翼部分在安全壳外部发生了反弹；由图8(b)可以看出，P4V1工况中的飞机撞击破坏现象，在t=0.08 s时，机头已经进入安全壳内部且机身未发生明显变形，从t=0.16～0.32 s，机身继续进入安全壳，此时飞机引擎和机翼也完成了撞击，引擎完全破坏，靠近机身的机翼机翼根部进入安全壳内部，机翼尾部沿安全壳两侧飞行；由图8(c)可以看出P5V1工况中的飞机撞击破坏现象。在t=0.08 s,t=0.16 s和t=0.24 s时，飞机未发生明显变形，都是从安全壳穹顶外侧飞过，未进入安全壳内部；在t=0.32 s时，靠近引擎的部分机翼发生变形，其他部位未发生明显变形，飞机仍未进入安全壳内部；在t=0.40 s时，飞机引擎发生变形，机翼的变形加大，飞机机身未见明显变形，飞机未进入安全壳内部，以上三种工况的飞机破坏现象为飞机撞击的典型现象。

3.1.2 飞机撞击力

飞机撞击力时程曲线如图9(a)～图9(e)所示。可知，在整个撞击过程中，撞击力呈先增大后减小趋势。在不同撞击速度下整个过程都可分为4个阶段，①T1-T2撞击阶段，撞击作用较为稳定，撞击力在某个值附近波动；②T2-T3撞击阶段，撞击力突然显著增大，图中曲线的斜率接近90°，短时间内达到撞击力峰值，各个初始撞击速度下等效钢梁筒身处和非等效钢梁筒身处撞击力峰值相较于第一阶段都增大3～4倍；③T3-T4当引擎完成撞击，仅有中部机身和剩余机翼与安全壳发生撞击，撞击力明显减小；④T4-T5撞击力曲线保持稳定波动，该时间段内与安全壳发生撞击的飞机部位为仅为后部机身。值得一提的是，P5位置处飞机与安全壳之间接触非垂直作用，飞机在撞击安全壳后飞行方向发生了向顶上偏移，与安全壳间的撞击作用较小，因此没有上述现象的发生。

图9(f)给出了所有工况下的飞机撞击力峰值。由图可知，各个位置下撞击力峰值随着速度的增加呈线性增加，对于筒身来说，P1位置撞击力峰值增加幅度为20%,23%,38%,73%，P2位置处撞击力峰值增加幅度为71%,78%,106%,150%。不同初始撞击速度下，筒身等效钢梁和非等效钢梁处的撞击力峰值差异有所不同，当速度为150 m/s时，P3处撞击力峰值比P2处大17%，在初始撞击速度为300 m/s时，筒身等效钢梁处P1和P3撞击峰值最大值达到了221.2 MN较筒身非等效钢梁P2处大30%，P4处大71%，P2和P4处的差异是由于P4位置处于筒身和穹顶的交界处，当飞机撞击时接触情况不同所导致。

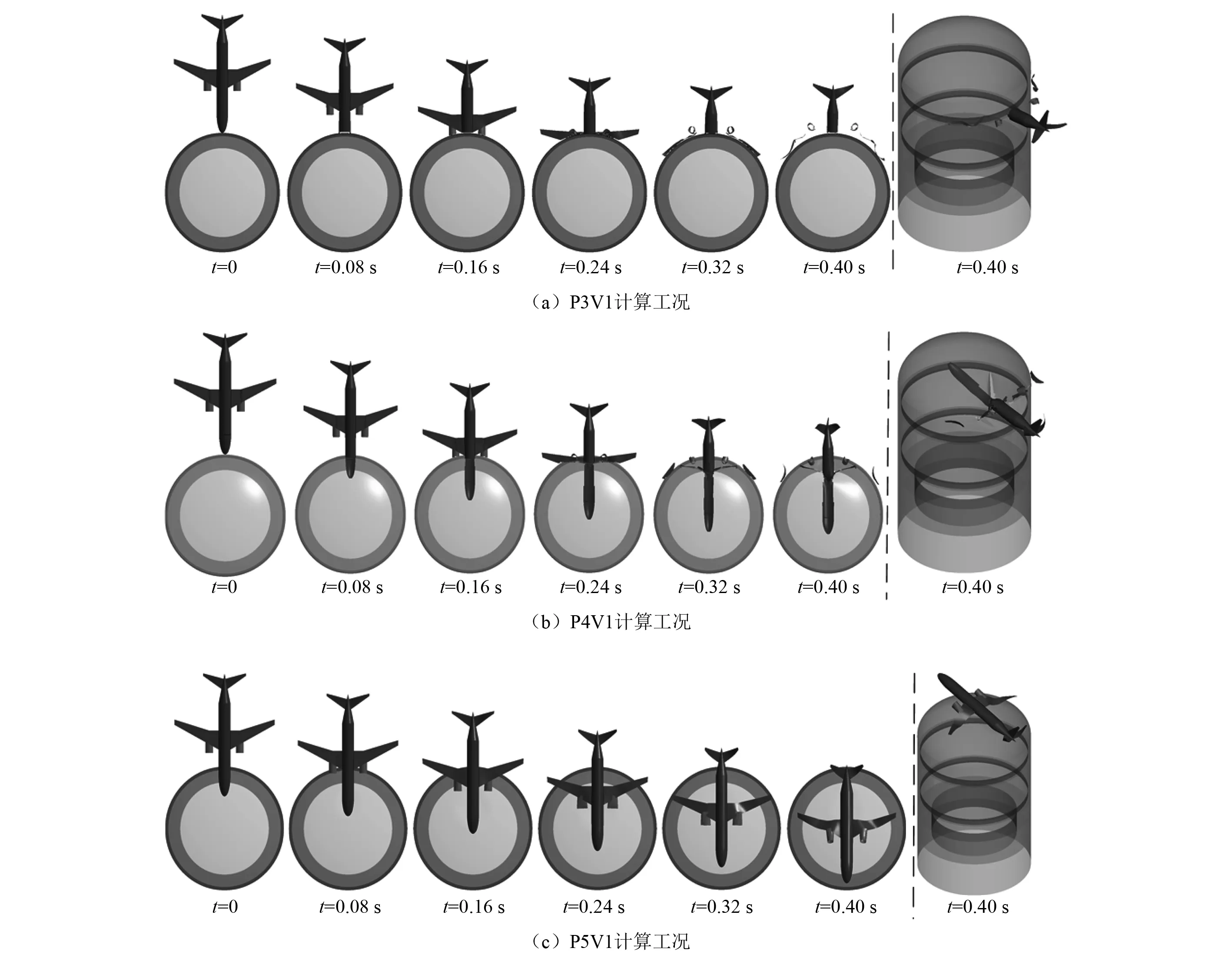
图8 飞机撞击破坏现象Fig.8 Aircraft crash damage

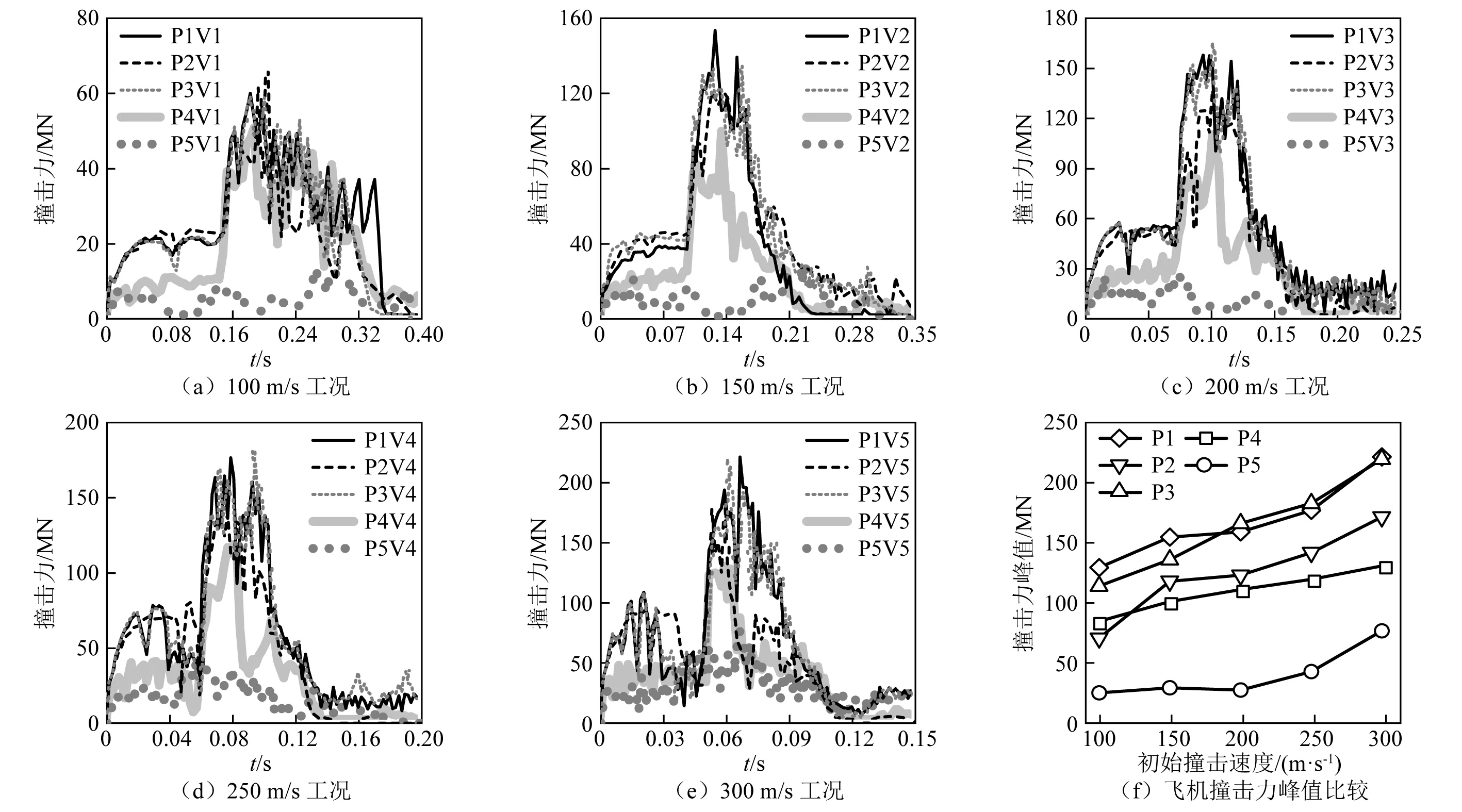
图9 飞机撞击力时程曲线及撞击力峰值比较Fig.9 Aircraft impact force-time history curve and comparison of maximum impact force

3.1.3 飞机动能分析

飞机动能时程曲线如图10(a)～图10(e)所示，对应不同初始撞击速度和撞击高度下的撞击末时刻的动能比较如图10(f)所示。由图可知，对于筒身来说，当初始撞击速度相同时，筒身安全壳钢梁位置(P1和P3)处的动能变化曲线几乎重合，在速度小于或等于200 m/s时，动能在撞击末时刻都几乎降为0，且动能损失速度要明显快于非钢梁位置(P2和P4)，P4位置在速度达到150 m/s时，末时刻仍有3×108N·m动能，当初始撞击速度达到300 m/s时，筒身等效钢梁处两条曲线几乎重合仍保持较快的动能损失，但筒身非等效钢梁处几乎和穹顶P5位置的曲线重合，说明该速度下筒身非等效钢梁处对飞机的阻碍作用非常小，以上都说明等效钢梁对于飞机的撞击有较好的抵抗效果。对于穹顶来说，飞机与安全壳接触面之间非垂直作用，与安全壳间的撞击作用较小，飞机有一定的速度损失，但在撞击末时刻仍能够离开安全壳上空继续飞行。由图10(f)撞击末时刻T5动能随初始撞击速度的变化情况也可以得到，筒身等效钢梁处对飞机的抵抗效果是最好的，在速度为300 m/s时，T5时刻飞机撞击筒身等效钢梁处的动能仅为其他撞击位置处的1/2。

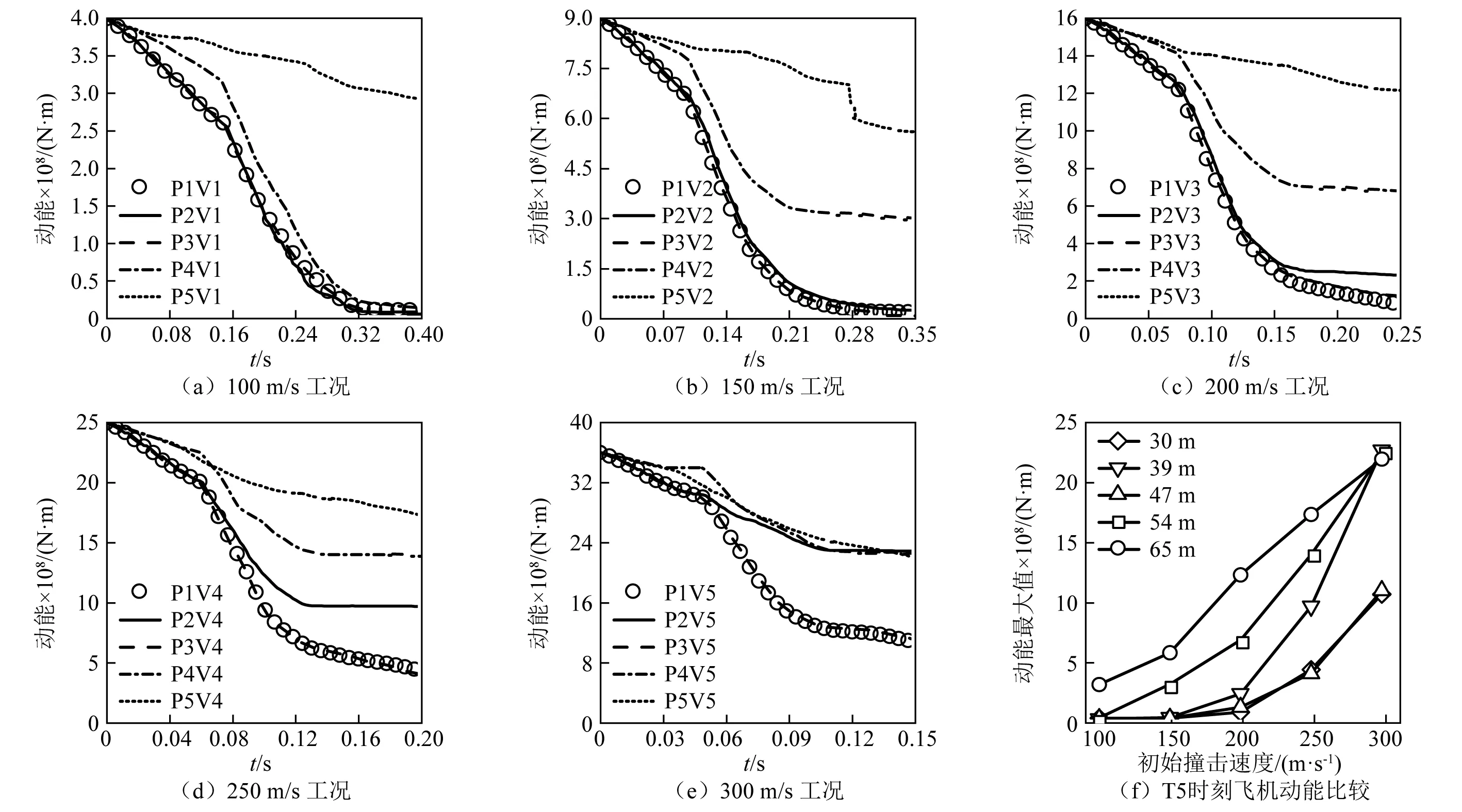
图10 飞机动能时程曲线及T5时刻动能比较Fig.10 Aircraft kinetic energy-time history curve and kinetic energy comparison at T5

3.2 安全壳位移响应及撞击区域破坏情况分析

3.2.1 位移响应分析

图11给出了不同初始撞击速度和撞击高度下，飞机撞击面沿安全壳高度分布的飞机撞击方向上水平位移峰值。由图11可知，在不同初始撞击速度和撞击高度下AP1000安全壳正面外壁水平向位移峰值均在各工况的飞机撞击所在位置处出现最大值，且随着初始撞击速度的增加而增大，其上下相邻高度处的正面外壁水平向位移峰值也均大于其他位置处，随着远离撞击中心，撞击位移逐渐衰减。在初始撞击速度小于等于150 m/s时，安全壳筒身等效钢梁部位P1(30 m)和P3(47 m)的撞击位移较小，最大只有1.62 m，筒身非等效钢梁处P2(39 m)和P4(54 m)的撞击位移较大，最大达到6.1 m，为前者的3.8倍。而当速度增加到200 m/s，情况正好相反，等效钢梁处P1和P3的撞击位移发生激增，30 m处的撞击位移最大达到了12.6 m。撞击穹顶处所有计算工况下的安全壳正面外壁水平向位移峰值在结构高度60 m及以内保持在很小值且均小于其他所有计算工况，可见此时安全壳撞击位置以下的安全壳筒体外壁沿飞机撞击方向未发生明显位移。

3.2.2 撞击区域破坏情况分析

安全壳在撞击区域的贯穿尺寸是安全壳动力响应和破坏情况的最直观反映。安全壳的具体环向和竖向贯穿尺寸结果，分别如表3和表4所示。部分工况撞击的安全壳撞击区域破坏情况图示，如图12所示。结果分析表明，在撞击高度为65 m的所有工况下，飞机撞击安全壳穹顶，穹顶外壁发生变形，但其均未发生贯穿。除上述未贯穿的计算工况外，飞机初始撞击速度为100 m/s时，安全壳等效钢梁位置处，安全壳的外壁钢板均发生内凹变形，但均未发生贯穿破坏，其余计算工况均发生贯穿破坏，且当撞击高度为54 m时，安全壳环向和竖向贯穿尺寸均大于同初始撞击速度下的尺寸，最大环向贯穿尺寸达到了29.68 m，最大竖向贯穿尺寸达到了17.86 m，可知钢制安全壳的最危险位置为安全壳圆筒形外壁与其穹顶的交界处，即高度为54 m处。根据不同速度下筒身等效钢梁位置和非等效钢梁位置的撞击破坏现象可知，筒身非等效钢梁处在速度为100 m/s时，就会发生贯穿破坏，环向贯穿尺寸为3.95，竖向贯穿尺寸为5.95，而等效钢梁处在速度达到150 m/s时，才会发生贯穿，且环向贯穿尺寸为2.71，竖向贯穿尺寸只有2.73，贯穿尺寸为前者的1/3；当初始撞击速度从100 m/s增加到250 m/s时，安全壳的环、竖向的贯穿尺寸都随之增加，在初始撞击速度为250 m/s时达到最大，但当初始撞击速度增加到300 m/s时，贯穿尺寸反而减小。

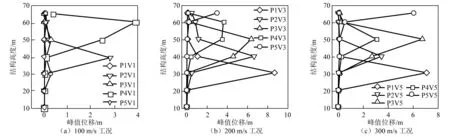
图11 AP1000安全壳正面沿撞击方向的位移峰值Fig.11 Peak displacement of AP1000 containment along the impact direction

图12 T5时刻的安全壳破坏情况图示Fig.12 Diagram of containment damage at T5

表3 安全壳环向贯穿尺寸Tab.3 Circumferential dimensions of containment

表4 安全壳竖向贯穿尺寸Tab.4 Vertical penetration dimension of containment

3.3 安全壳等效应力分布

图13为AP1000核岛结构安全壳P3和P4在不同初始撞击速度下的等效应力云图，选择这两个位置的原因是，P3为等效钢梁位置，P4是非等效钢梁位置，可以比较两者的应力发展情况，且由前面的分析可知，P4是贯穿破坏最严重的区域。为了更加明确和比较钢制安全壳的应力集中现象和安全壳的失效，应力云图统一为最大应力边界条件。观察图12中AP1000安全壳外壁等效应力云图可以看出，在不同撞击位置处，安全壳的等效应力主要集中在正面区域，安全壳正面的损伤破坏区域形状基本相同，等效最大应力最开始出现于撞击中心区域，机身撞击区域呈圆形，随着撞击的继续进行，安全壳上最大等效应力范围先是沿高度方向扩展，当引擎和机翼撞击安全壳时，安全壳上最大等效应力范围开始沿水平方向扩展，且撞击中心区域最大等效应力分布范围增大。等效应力的最大值都是出现在安全壳撞击中心区域处，且此处外壁钢板产生的最大等效应力均已超过安全壳钢材的屈服应力415 MPa。由等效应力图的发展情况来看，当初始撞击速度相同时，P3位置等效应力影响范围要明显大于P4位置，P4的撞击等效应力更为集中，在t2和t3时刻，P3位置对整个安全壳正面都有一定的影响，在P1位置处都有一定的钢材达到屈服应力，而P4位置都集中在撞击点附近。

图13 安全壳等效应力云图Fig.13 Equivalent stress contours of the containment

4 结 论

基于已验证的波音737 MAX 8大型商用飞机和AP1000安全壳，采用ANSYS/LS-DYNA软件进行了25种工况下飞机撞击安全壳全过程数值模拟，分析了飞机和安全壳结构的动力响应、安全壳的局部破坏和等效应力分布。结论如下：

(1)基于弹-靶体接触耦合分析方法能有效预测飞机撞击动力过程与效应，与Riera法理论计算结果相比，飞机撞击力峰值和冲量的最大误差仅为1.11%，3.73%。

(2)飞机撞击力时程曲线先增大至峰值后减小，其峰值出现在第二阶段，且该阶段的整个撞击力主要由引擎撞击贡献，撞击力峰值相较于第一阶段增大3～4倍。

(3)不同初始撞击速度下，筒身等效钢梁处的撞击力峰值较非等效钢梁处大，最小为后者的117%(速度为150 m/s)，最大达到了后者的171%(速度为300 m/s)。

(4)等效钢梁能够很好地抵御飞机的撞击作用。在初始撞击速度为100 m/s时，筒身非等效钢梁处已经贯穿破坏，环向贯穿尺寸为3.95 m，竖向贯穿尺寸为5.95 m，而等效钢梁处在初始撞击速度达到150 m/s时才发生贯穿破坏，且环向、竖向贯穿尺寸分别为2.71 m，2.73 m，贯穿尺寸仅约为前者的1/3，且撞击等效钢梁后飞机动能下降最快，在T5时刻飞机撞击筒身等效钢梁处的动能仅为其他撞击位置处的1/2(初始撞击速度为300 m/s)。

(5)安全壳筒身段与穹顶的交界处为安全壳结构的最危险位置(54 m高度处)，在各个初始撞击速度下都发生了贯穿破坏，且在此位置处安全壳环向和竖向贯穿尺寸均大于同初始撞击速度下其他位置的贯穿尺寸，最大环向、竖向贯穿尺寸达到了29.68 m，17.86 m。安全壳穹顶在所有工况的飞机撞击下均未发生贯穿破坏(撞击高度为65 m)，撞击使飞机的飞行方向发生变化，均向安全壳斜上方飞出。

(6)当飞机撞击速度超过150 m/s时，安全壳撞击的钢板等效应力影响范围随初始撞击速度的增加而减少，且撞击等效钢梁处的安全壳等效应力分布范围相对于撞击非等效钢梁处的更大。