细长圆柱构件表面扰流降噪机理的研究

2022-05-30张石宸王春江孙向东

振动与冲击 2022年10期

张石宸，王春江，孙向东，常邑

(1.上海交通大学船舶海洋与建筑工程学院，上海 200240；2.中车青岛四方机车车辆股份有限公司，山东青岛 266111)

钝体绕流现象普遍存在于工程领域，已有研究大多针对扰流流动特性，针对绕流引发噪声研究相对较少。绕流诱发噪声为气动噪声，其成因与尾流涡脱相关，当涡旋从钝体上脱落，引起钝体表面反方向的环流，改变表面压力诱发气动噪声。目前气动噪声研究常见亚声速或声速的交通、电力领域，如高速列车受电弓、飞机起落架、风力发电机和输电线等。此外，绕流引发气动噪声与速度6～8次方相关，亚声速或声速下噪声声压较大，严重影响人们的生活，因此降低钝体绕流气动噪声尤为重要。

1 钝体绕流降噪措施

考虑钝体绕流噪声与速度的相关律，降噪减噪显得十分重要，过去20年间提出了一些主动和被动降噪技术。主动降噪方面，Hao等[1]数值仿真证明了涡流发生器可以有效地控制圆柱表面流动，降低绕流噪声。Siozos-Rousoulis等[2]以圆柱-翼结构为对象，对旋转振动圆柱对翼型气动噪声的影响进行了数值研究。Du等[3]和Ma等[4]研究了受迫振动圆柱的绕流噪声与振动参数的关系。被动降噪方面，多孔介质覆盖经数值[5]和试验[6-7]验证是非常有效的降噪措施。文献[8]在光滑圆柱表面引入不同形式的凸环结构，发现一些仿生结构对钝体绕流噪声有抑制作用。Li等[9]试验研究了螺旋凸环对串联圆柱气动噪声的控制效果，试验结果表明，螺旋凸环能有效降低圆柱气动噪声，串联布置时，控制前柱或者同时控制前后柱均可以获得较好的降噪效果。李鑫等[10]建立了二维翼型的单点多目标优化设计系统降低翼型气动噪声。

众多研究结果表明，许多降噪技术对钝体绕流噪声均有较好的抑制作用，但是关于降噪的工作大多是对钝体气动噪声的试验测量或数值计算，获得降噪规律，研究较少涉及钝体附近湍流流场特征分析，关于降噪技术包含的降噪机理仍不清楚，需要进一步的研究。本文通过数值仿真研究不同高度的双侧扰流条对圆柱钝体绕流噪声的影响，可以获得圆柱附近详细的流场信息，旨在分析扰流条的降噪机理，并确定最优的扰流条截面高度直径比。

2 数值模拟设置

2.1 声流场模拟方法

本文通过大涡模拟获得圆柱表面压力脉动信息，作为声源项并通过FW-H积分方程计算出圆柱绕流远场噪声。大涡模拟采用商用软件Starccm+作为求解器，大涡模拟采用壁面适应局部涡黏模型(wall-adapting local eddy-viscosity,WALE)模型。

LES计算域展向长度受到计算资源限制，因此数值模拟声学验证中，本文分别应用Kato公式[11]和Perot公式[12]修正FW-H测点声压级(sound pressure level,SPL)与Casalino等的试验SPL对比。Kato公式引入展向相关尺度Lc考虑相位偏移的影响，将声压叠加分为三类：

当Lc≤Lz时，

当Lz≤Lc≤L时，

(1)

当L≤Lc时，

而Perot等给出了与展向相关尺度无关，与接收点至声源距离R相关的修正公式，

(2)

式中：SPLs为FW-H测点声压级；SPL为公式修正声压级；Lz为计算域展向长度；L为试验圆柱展向长度。展向相关尺度Lc与流场中位置和频率相关，但为了简单起见大多数文献在关注频率范围内采用相同Lc，本文计算工况与文献[13]一致，因此本文展向相关尺度取其试验值Lc=6.5D。

2.2 圆柱仿真设置

圆柱仿真几何参数和网格拓扑如图1(a)所示。x方向与来流速度U∞方向相同，y方向垂直于来流方向，z方向沿着圆柱轴向。本文中圆柱横截面直径D=0.016 m。

计算域为三维圆柱形域，流域半径R=25D，设置自由流边界条件，U∞=20 m/s，Mach∞=0.06，雷诺数Re约为22 000，Re=U∞D/υ。展向长度Lz=2D，根据文献[14]的建议，侧向边界设置为对称边界条件，若应用周期边界条件会人为限定计算中展向相关尺度Lc的范围。网格划分方式采用结构化网格，圆柱上第一层壁面网格厚度为0.008 mm，其y+≤1，增长比取为1.15，边界层网格厚度为2 mm。近壁面加密区网格尺寸为0.5 mm，尾流加密区网格尺寸为1 mm，网格总数约为220万；时间步长采用1×10-5s，满足CFL (courant-friedrichs-lewy)数在计算域小于1的要求[15]。

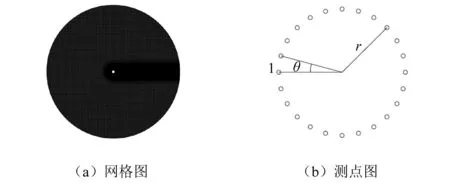
图1 网格拓扑和测点布置图Fig.1 View of mesh

FW-H声学测点位于过圆柱中心的x-y平面上，测点与圆柱中心距离为r=1.38 m，相邻测点间夹角θ=15°，0°测点编号为1，顺着逆时针方向编号依次增大，如图1(b)所示，共24个声学测点。压力测点的平面、角度间隔以及编号与噪声测点相同，位于圆柱表面上。数值模拟在上海交通大学36核工作站机上运行，以光滑圆柱算例为例，计算共采用18个处理器，以稳态雷诺时均(reynolds-averaged navier-stokes equations, RANS)计算结果作为大涡模拟(large eddy simulation, LES)初始条件，LES模拟个4×103时间步后流场达到稳定后，再运行1.2×104个时间步进行流场及声学数据的采集。

2.3 仿真模型设置验证

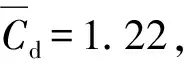
图2 升阻力系数时程(T=tU∞/D)Fig.2 Time history of lift and drag coefficients

图3 光滑圆柱压力脉动系数均方根Fig.3 Root mean square of pressure fluctuation coefficient around cylinder

根据Casalino等研究中声学测点布置及声学结果，把声学测点1的数值模拟结果与试验结果对比分析，如图4所示，数值仿真得到的修正声压值与试验值吻合较好。

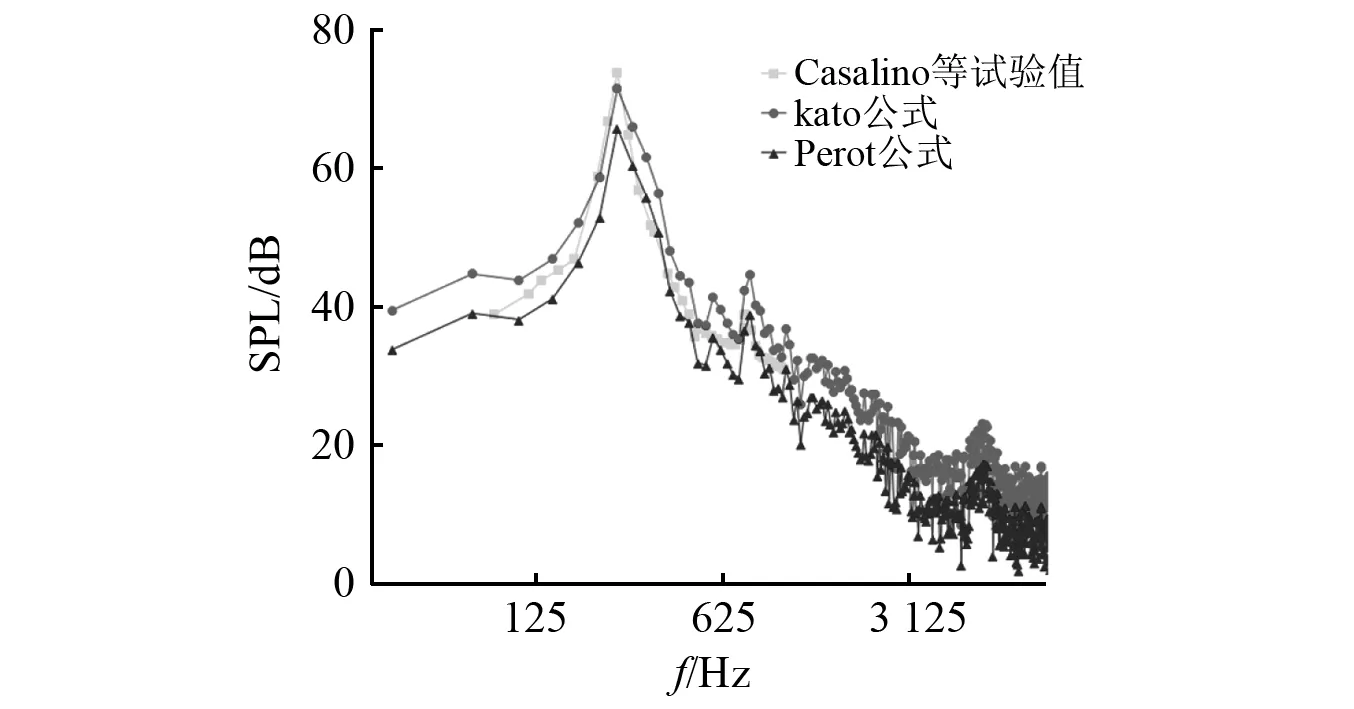
图4 SPL对比图Fig.4 Comparison of SPL

3 圆柱流场分析

为了更好理解圆柱表面附近流场和气动噪声特性，本章对流场计算结果进一步分析。

3.1 光滑圆柱流场

图5为某个涡脱周期内升力系数达到最大值时圆柱中心处x-y平面瞬时速度云图和流线分布图，发现光滑圆柱尾迹中回流具有向上游发展的趋势。

图5 光滑圆柱流线图和速度云图Fig.5 Streamlines and velocity contours around cylinder

图6(a)、图6(b)、图6(c)分别为圆柱中心y-z平面Z轴瞬时涡量图，X轴瞬时涡量图和Y轴瞬时涡量图。从Z轴瞬时涡量图中可以看出，圆柱尾流中分布着沿流向的条带结构，这与圆柱上下表面交替脱落的涡旋相关，表明尾流区具有较强的展向相关性。而尾流中X轴涡量和Y轴涡量分布比较无序，相比于Z轴涡量，涡量幅值较小。

图7(a)、图7(b)、图7(c)分别为尾流区域湍流强度Tux,Tuy,Tuz分布规律，发现湍流集中在圆柱下游1D～2D中，并呈现出明显的对称性。自分离点开始，流向湍流强度Tux随着分离剪切层的发展逐渐增大。当涡旋脱落时，Tux达到最大幅值49.52%。横向湍流度Tuy和展向湍流度Tuz最大幅值分别为73.53%和30.43%。

根据Farassat提出的声压积分公式，荷载噪声与积分面的压力脉动变化率相关，压力脉动变化越快，辐射噪声能力越强。参考图3所示的圆柱表面压力脉动系数均方根图，可以看出，圆柱上表面70°～90°区域内压力脉动系数均方根较大，其中上表面处压力脉动系数均方根最大为0.36左右，上表面80°处为雷诺数Re=22 000时圆柱绕流分离点。在0°～70°区域，即圆柱分离点前区域，压力脉动系数均方根急剧减小，在0°处减少为0。

图6 光滑圆柱瞬时涡量分布(s-1)Fig.6 Distribution of instantaneous vorticity around cylinder(s-1)

图7 光滑圆柱湍流强度(%)Fig.7 Turbulence intensity around cylinder(%)

根据Achenbach[17]对光滑圆柱气流绕流模式的研究，在亚临界区，圆柱绕流流动有相近规律，气流在70°～90°分离，分离剪切层失稳形成涡团脱落，导致圆柱体表面气压脉动力震荡，辐射噪声。若采取降噪措施，如多孔材料涂层、仿生学改型、边界层吸气或吹气等，根据降噪措施作用机理的不同，应设置在圆柱表面不同位置。

3.2 扰流圆柱流场

为抑制分离剪切层失稳，在圆柱绕流分离点后140°和220°处引入截面为长方形扰流条作为表面扰流装置，鉴于Casalino等指出扰流条降噪效果主要与截面高度直径比H/D相关，本文中扰流条截面宽度直径比W/D=1/4。通过改变截面高度直径比H/D探究扰流条对圆柱流场以及表面声源位置的影响。

图8为涡脱周期升力系数达到最大值时x-y平面的瞬时速度云图，发现扰流条圆柱绕流形成的分离泡长度增加，说明扰流条推迟了涡旋脱落位置。当扰流条的高度直径比H/D从1/8增加为1/4时，扰流条恰好接触圆柱分离剪切层下表面，随着扰流条高度继续增加，剪切层在扰流条表面再附着。

图8 扰流条圆柱瞬时速度云图(m/s)Fig.8 Comparison of instantaneous velocity around cylinder with strips(m/s)

图9为扰流条圆柱涡脱周期升力系数达到最大值时y-z平面的瞬时Z轴涡量云图。与光滑圆柱尾流涡量相比，近尾流区域三个方向涡量幅值下降，原因是扰流条使涡旋核心向下游移动，远离圆柱。当H/D由1/8变化为1/4时，Z轴涡量图中条带结构反而贴近圆柱；当H/D>1/4时，随着扰流条高度增加，Z轴涡量图中条带结构逐渐远离圆柱。此外，虽然扰流条圆柱尾流中仍存在沿流向分布的条带结构，但条带结构扭曲，说明扰流条破坏了大涡结构的展向相关性，使得圆柱表面压力脉动存在较大相位差。

为进一步分析扰流条对圆柱绕流涡结构的影响，图10(a)以H/D=3/8扰流条圆柱为例，给出了扰流条圆柱尾流Q准则等值面图(Q=7×106s-2)。同图10(b)对比可知，随着扰流条高度增加，大尺度涡旋未明显削弱，只是形成位置向下游偏移。在大尺度涡结构和圆柱之间的尾流区域，分布着许多小尺度涡旋。因此，相比于光滑圆柱，扰流条圆柱尾流中涡量略微增大。Powell涡声方程认为涡是气动发声的根源。因此扰流条圆柱近尾流区域大量小涡团形成，会引起高频段辐射噪声的增加。

图9 扰流条圆柱瞬时Z轴涡量分布(s-1)Fig.9 Distribution of instantaneous Z-axis vorticity around cylinder with strips(s-1)

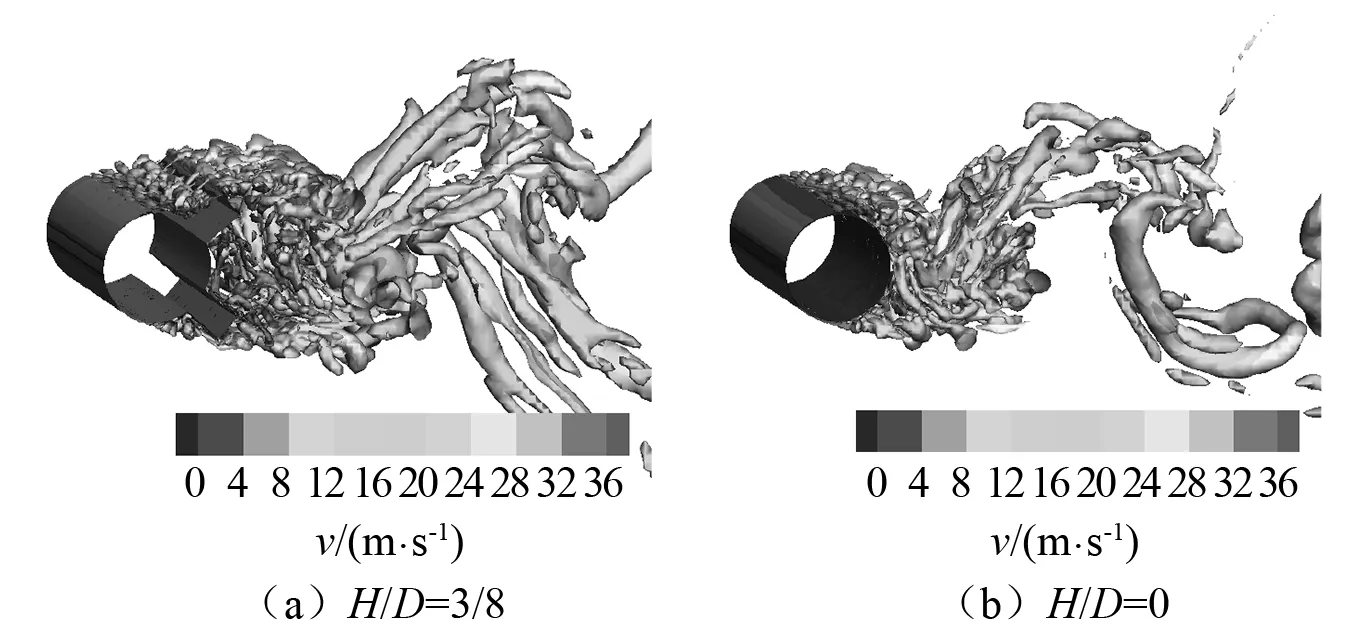
图10 Q准则等值面图(Q=7×106 s-2)Fig.10 Iso-surfaces of Q criterion(Q=7×106 s-2)

圆柱近尾流中的湍流脉动对圆柱表面的压力脉动存在直接影响，因此图11～图13分别给出扰流条圆柱x-y平面湍流强度Tux,Tuy,Tuz云图。与光滑圆柱相比，当扰流条H/D<1/2时，扰流条圆柱附近流域中流向、展向以及横向湍流度均明显降低，其中H/D=3/8扰流条圆柱附近湍流强度最小。然而，当分离剪切层接触扰流条或者再附着在扰流条上时，扰流条会增加分离剪切层中流体动能，因此当H/D>1/8时，尾流区域中湍流度增强。对比H/D=1/4扰流条圆柱与H/D=3/8扰流条圆柱，发现后者湍流强度反而小于前者湍流强度，原因是当H/D=1/4时，扰流条恰好与剪切层下表面接触，促进了边界层的不稳定增长，而当H/D=3/8时，虽然剪切层再附着在扰流条上游，但是附着距离较短，补充动能较少。当H/D=1/2时，再附着距离增大，对下游剪切层增长提供了大量动能，圆柱尾流区域湍流度显著增大。

图11 扰流条圆柱流向湍流强度Tux (%)Fig.11 Comparison of turbulent intensity Tux around cylinder with strip(%)

图12 扰流条圆柱流向湍流强度Tuy (%)Fig.12 Comparison of turbulent intensity Tuy around cylinder with strip(%)

图13 扰流条圆柱流向湍流强度Tuz (%)Fig.13 Comparison of turbulent intensity Tuz around cylinder with strips(%)

图14给出了扰流条圆柱中心x-y平面上压力脉动均方根分布。结合图8可以看出相对于光滑圆柱，扰流条阻碍了尾流中的回流向上发展，并在上游形成滞留涡结构，抑制了圆柱上下表面压力脉动，其中H/D=3/8扰流条圆柱表面压力脉动最小，其次是H/D=1/2扰流条圆柱，H/D=1/8扰流条圆柱和H/D=1/4扰流条圆柱；在扰流条表面以及扰流条下游，H/D=1/8扰流条圆柱和H/D=3/8扰流条圆柱表面压力脉动较小，而H/D=1/4扰流条圆柱和H/D=1/2扰流条圆柱压力脉动略大于光滑圆柱表面压力脉动，原因是前两工况下尾流分离涡内不仅包含主涡旋，还在扰流条和圆柱尾缘附近分布有涡旋，降低了扰流条下游湍流强度，抑制了圆柱表面压力脉动。

图14 扰流条圆柱压力脉动系数均方根Fig.14 Root mean square of pressure fluctuation coefficient around cylinder withstrips

图15给出了圆柱表面90°处展向相关系数规律，可以看出引入扰流条后，圆柱表面展向相关性下降，当H/D=3/8时，圆柱上下表面压力脉动几乎不相关，说明扰流条破坏了三维大尺度涡结构的展向相关性，从而削弱了圆柱表面噪声辐射。

图15 圆柱表面展向相关系数Fig.15 Spanwise correlation coefficient on cylinder

4 圆柱声场分析

图16给出了90°方向上的7号噪声测点获得的各工况下噪声频谱对比图。由图16可知，光滑圆柱自然频率为250 Hz，其对应声压值为56.59 dB，圆柱双侧添加高度直径比H/D分别为1/8, 1/4, 3/8, 1/2扰流条后，自然频率分别改变为349.28 Hz,257.34 Hz, 209.57 Hz, 190.66 Hz，声压值分别为42.26 dB,45.40 dB,38.42 dB, 41.62 dB。在圆柱两侧添加截面为长方形的扰流条，导致圆柱绕流噪声频谱中波峰频率发生改变，当H/D=1/8时，圆柱自然频率增加；当H/D>1/2时，扰流条高度增加，圆柱自然频率减小。关于声压，四种高度扰流条对圆柱绕流噪声中的单音噪声成分均有显著的抑制作用，并且由于圆柱近尾流区域大量小涡团形成引起涡量增加，一定程度上增加了高频段宽频噪声幅值。特别地，H/D=3/8的扰流条对圆柱绕流的单音噪声抑制效果最佳，噪声降低达到18.17 dB。根据第三章不同高度扰流条圆柱流线图以及表面压力脉动均方根分布，本文认为扰流条的引入改变了圆柱流动特性，破坏了圆柱绕流的展向相关性，减弱了大尺度涡结构。同时扰流条上游出现滞留涡，抑制了圆柱上下表面压力脉动。然而，扰流条增加，分离剪切层在扰流条表面发生再附着现象，为剪切层在扰流条下游失稳卷曲补充动能，因此当扰流条H/D由3/8增加到1/2时，扰流条表面压力脉动均方根增大，削弱扰流条降噪效果。

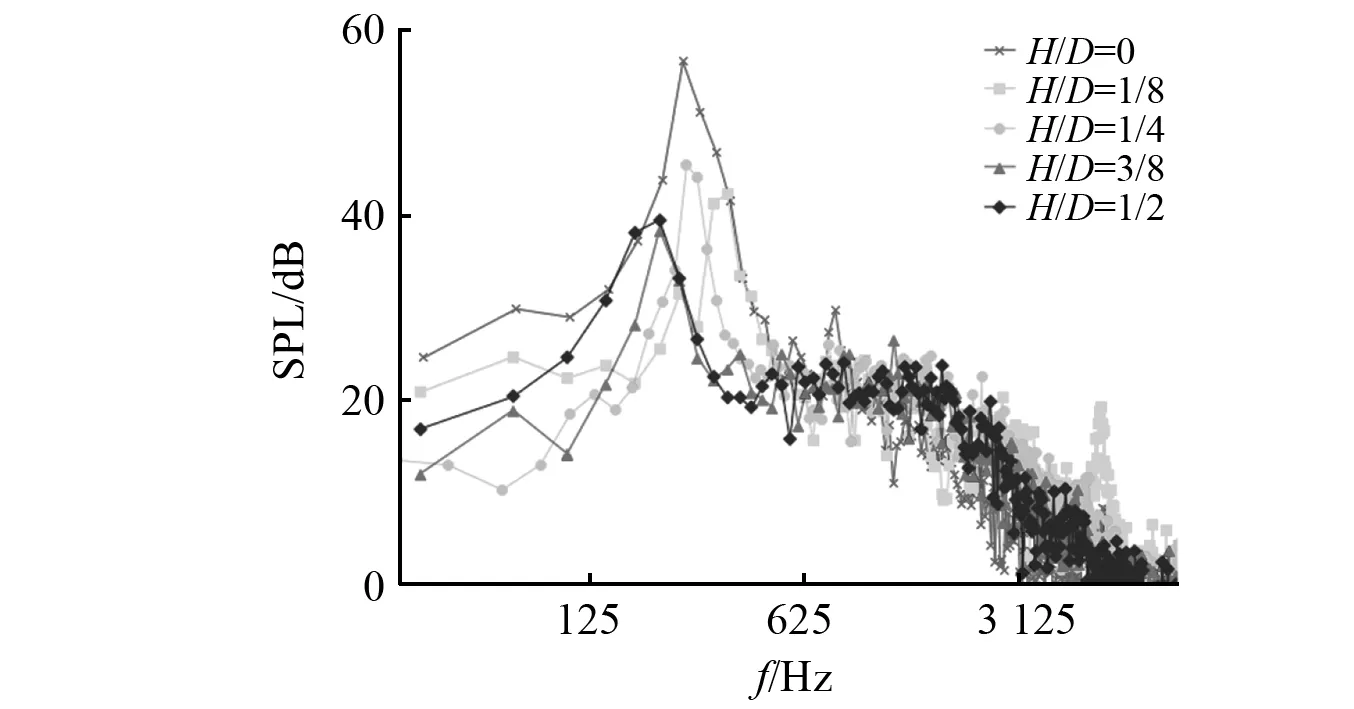
图16 不同工况SPL图Fig.16 SPL of different cylinders

图17为5种工况下圆柱辐射噪声指向性图，光滑圆柱表现出明显的偶极子噪声指向性，不同指向总声压级(overall sound pressure level，OASPL)的最大差值为15.5 dB，噪声辐射次要方向(0°,180°方向)对应声压与噪声辐射主要方向(90°,270°方向)对应声压相比，次要方向声压可以忽略不计；圆柱双侧添加扰流条措施后，圆柱噪声的偶极子噪声指向性特征逐渐消失。当H/D=1/8或H/D=3/8时，扰流条对任意方向噪声均有降噪效果；当H/D=1/4或H/D=1/2时，在和噪声辐射区间，扰流条仍保持较好的降噪效果，但在噪声辐射次要方向噪声，扰流条增加了噪声声压值2～4 dB，这与扰流条表面显著增大的压力脉动相关。综上所述，本文认为扰流条引入降低了圆柱绕流噪声，特别地，当扰流条高度直径比H/D=3/8时，扰流条的降噪效果最好。