黏性剪切阻尼器性能频率依存性对斜拉索多模态阻尼影响研究

孙利民， 孙浚杰， 陈 林

(1. 同济大学 土木工程学院，上海 200092；2. 同济大学 土木工程防灾国家重点实验室，上海 200092)

缆索承重结构具有卓越的跨越能力，在土木建筑结构中受到了广泛地运用，常见的包括斜拉桥、悬索桥等。对于斜拉桥，拉索作为主要传力构件，对桥梁的安全至关重要。近几十年来，随着桥梁跨径的逐渐增大，目前斜拉索长度已经接近600 m。然而，作为一种细长构件，由于拉索横向刚度小、自身阻尼低的特点，在风及风雨耦合作用下常出现明显振动，甚至是大幅振动。常见的风致振动包括抖振、涡振、驰振和风雨激振等，其中属风雨激振最为剧烈，具有自激和发散特性[1-2]。风雨激振最早在日本Meiko-Nishi桥上观察到，后来在美国休斯顿的Fred Hartman大桥、中国上海的杨浦大桥、丹麦的Faroe大桥上均有发现[3]。风雨激振发生时的风速较低，通常在8～15 m/s左右；振动频率一般小于3 Hz，此频段内涵盖了拉索的多个低阶模态；振动幅值约1 m，甚至可引起相邻拉索的碰撞，严重危害索及锚固结构的疲劳寿命和桥梁的适用性。

为了控制拉索的振动，工程中常采用的控制方法有：①对索表面进行气动措施处置，目的是打破拉索与风雨的耦合机制；②在索端安装阻尼器，增大对横向振动的耗能效果[4]；③在索间设置辅助索，提高索的整体刚度和耗能效果[5]。其中，在索端安装阻尼器的方法能显著增加索的模态阻尼，对拉索不同机理和模态的振动均有抑制效果，是目前拉索振动控制最为有效，研究得最为透彻的方法之一[6]。对于拉索阻尼器系统，早期研究均将索模拟为一根张紧弦，将阻尼器考虑为理想的黏滞阻尼器，关注索的一阶阻尼。例如，Yoneda等[7]结合工程经验，近似得到了阻尼器安装在拉索锚固的一阶模态阻尼比。随后，Uno等[8]引入了无量纲参数的分析方法，极大简化了阻尼器设计计算。Pacheco等[9]运用伽辽金法计算了理想张紧弦-黏滞阻尼器系统的模态阻尼比，得到了通用的阻尼器设计曲线。他们的结论是，对于参数一定的拉索，最大附加阻尼比仅与阻尼器安装位置有关；同时，通过自由衰减试验发现试验所得最大模态阻尼比远小于理论值，猜测极有可能的影响因素来自于阻尼器的非线性、刚度等特性。

此后，模拟真实拉索阻尼器系统得到了学界更多的关注，对相关特性进行了大量研究。Xu等[10]用混合法研究了实际拉索的垂度的影响，Tabatabai等[11]研究了考虑拉索抗弯刚度的阻尼器减振效果。所得结果表明，抗弯刚度对所获得的模态阻尼比有较大影响，但拉索垂度主要对一阶模态阻尼比有影响。进而，Krenk等[12]推导了拉索模态阻尼比的解析表达式，并给出了前几阶模态阻尼比的渐近式；采用同样的方法，Krenk等[13]进而考虑了索垂度对系统动力特性的影响。Main等[14]详细分析了阻尼器位于索上任意位置时对索频率和阻尼的改变作用，他们进而考虑了索抗弯刚度的影响[15]。通过实索阻尼器试验，周海俊等[16-17]发现阻尼器及其连接支撑性能对其减振效果有显著影响。周亚刚等[18]进而建立了拉索-三单元Maxwell模型考虑阻尼器内刚度和支架柔度的影响，发现两者均会显著削弱阻尼器的减振效果；周海俊等[19]通过复模态理论分析，得到了考虑阻尼器的内刚度索模态阻尼比表达式。同时，Fujino等[20]综合考虑了索刚度、阻尼器刚度和支撑柔度的影响，Duan等[21]探讨了额外阻尼器质量的影响。梁栋等[22]研究发现主梁振动会削弱安装在索梁间的阻尼器对拉索的减振效果。Sun等[23]采用分数阶模型扩展现有拉索-黏滞阻尼器系统，更好地模拟了索阻尼器力与位移的普遍规律。同时，阻尼器的非线性对其阻尼效果的影响也受到了研究者的关注[24-26]。

为了提升阻尼器对拉索的阻尼效果以解决超长拉索的振动控制问题，较多研究提出了基于磁流变阻尼器的方案和算法[27-28]，近年来，更多的研究关注被动阻尼器减振效果的提升策略，例如Chen等[29]提出采用负刚度阻尼器实现阻尼效果的提升，李寿英等[30-31]研究了多种黏滞惯性质量阻尼器对拉索的减振效果。

前述所涉及的文献主要关注阻尼器对索特定模态的阻尼效果及对应的阻尼器参数。实际工程中的阻尼器设计需要针对索多阶振动模态[32]，比如针对拉索 0～3.0 Hz易出现风雨振的低阶振动模态。假定阻尼器性能参数不受频率影响，如果阻尼器针对某一特定模态设计，其在此模态下达到最佳性能，则在高阶模态下将会过于刚性，而在较低模态下则会过于柔弱。同时，现有多种阻尼器的理论和试验研究中，发现绝大多数阻尼器的性能都表现出频率依存性的特点。例如在日本和中国广泛应用的拉索减振阻尼器中的黏性剪切阻尼器(viscous-shear damper，VSD)，在固定位移幅值下，随着振动频率的增大其等效阻尼系数变小而刚度系数增大[33-34]。注意到，阻尼系数随频率增大而减小是有利于拉索的多阶振动控制的，因为高阶振动的最优阻尼系数小于低阶模态对应的最优阻尼系数。但是，刚度系数的增加则会削弱高阶振动的阻尼性能。然而，截至目前，对于阻尼器性能的频率依存性还没有得到充分的考虑，因此，本文考虑阻尼器性能频率依存性的减振研究就表现出了明显的实用性。

针对上述问题，本文通过阻尼器单体试验、理论分析和实索试验验证三个方面，对比研究阻尼器性能频率依存性对拉索多模态振效果的影响，并提出了一套实用的考虑阻尼器性能频率依存性的设计方法。

1 黏性剪切阻尼器单体性能试验研究

1.1 黏性剪切阻尼器

黏性剪切阻尼器在斜拉索振动控制中应用广泛，典型的VSD包括两个主要部分，即装有黏性介质的箱体和一个浸入黏性介质的可移动剪切板，如图1所示。当剪切板相对套箱移动时，由于黏性介质的抗剪作用将会产生一个反力。同时假定移动板和套箱边板之间的黏性介质厚度在运动过程中保持一致，那么反力的大小主要取决于介质的黏性、剪切板之间的黏性介质厚度和总剪切面积。从图1可知，VSD不同于常见的油阻尼器、液压阻尼器，其结构简单，没有诸如密封圈、阀门、活塞、球铰等高费用且脆弱的部件，因此具有良好的经济性、耐久性和易维护性。拉索参数如表1所示。

图1 黏性剪切阻尼器构造图Fig.1 A schematic diagram of the viscous-shear damper

表1 拉索参数表Tab.1 Cable parameters

1.2 阻尼器单体测试试验

针对表1苏通大桥的一根斜拉索，本研究设计制作了一个VSD，首先在实验室的液压伺服机上进行试验，如图2所示。利用最大出力10 kN的由计算机控制的作动器对VSD施加正弦强迫位移。考虑到后续实桥测试中能激起的拉索振幅一般较小，阻尼器的变形幅值较小，因此测试关注阻尼器的变形幅值约为5 mm时的性能。试验中同步记录阻尼器的变形和对应的阻尼器出力，采样频率为100 Hz。强迫振动的频率根据对应拉索的振动模态频率选取。

图2 实验室内测试时的阻尼器Fig.2 The viscous-shear damper in laboratory testing

VSD的试验结果如图3所示。图3(a)为VSD在确定振动幅值下，四种不同频率的强迫正弦位移加载条件下的出力-位移曲线；图3(b)为相应的出力-速度曲线。从图3(a)可知，在最初的几个周期中有明显的出力衰减并且在几个周期后稳定。在试验中，为了使出力曲线稳定，每次试验进行10个周期的加载。

图3 单体试验示例Fig.3 Examples of laboratory testing results of the viscous-shear damper

1.3 阻尼器性能的频率依存性

阻尼器性能试验得到的出力-位移曲线近似为一倾斜的椭圆，见图3。表明阻尼器表现出弹簧的力学行为，即阻尼器具有内刚度作用。因此，选取Kelvin-Voigt模型模拟VSD的动力特性，其出力公式为

(1)

对于每个固定频率和振幅的测试工况，根据最后一个加载周期的出力和位移利用最小方差法拟合其等效刚度系数kd和阻尼系数cd。图4对比了根据Kelvin-Voigt模型识别出的参数和强迫位移、速度时程得到的出力-位移曲线和出力-速度曲线与图3中的实测曲线。注意图4只绘制了实测的最后一个周期的曲线用于对比。从图4可知，Kelvin-Voigt模型在给定位移和速度下足以精确地推算出VSD阻尼器的出力。

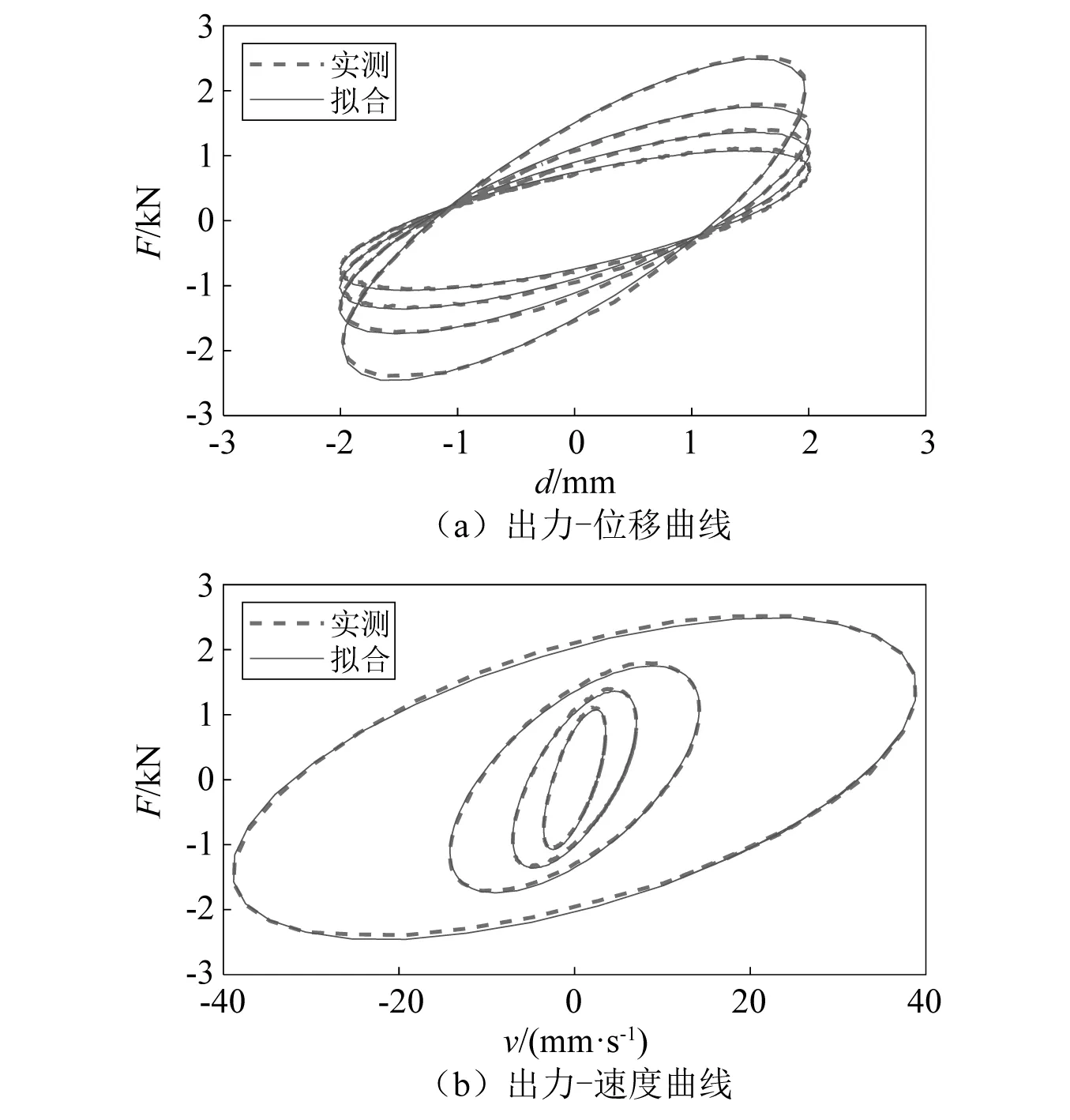
图4 试验结果与识别结果对比Fig.4 Comparison of laboratory testing results and the fitted model

固定阻尼器的变形幅值，发现在不同频率下，阻尼器的刚度系数、阻尼系数随着频率变化而出现显著变化。分别采用如下近似关系描述VSD刚度和阻尼系数的频率依存性

(2)

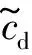
(3)

图5绘制了拟合函数在频率0～6 Hz拟合的VSD刚度和阻尼系数，实测的结果在图中采用星号表示。

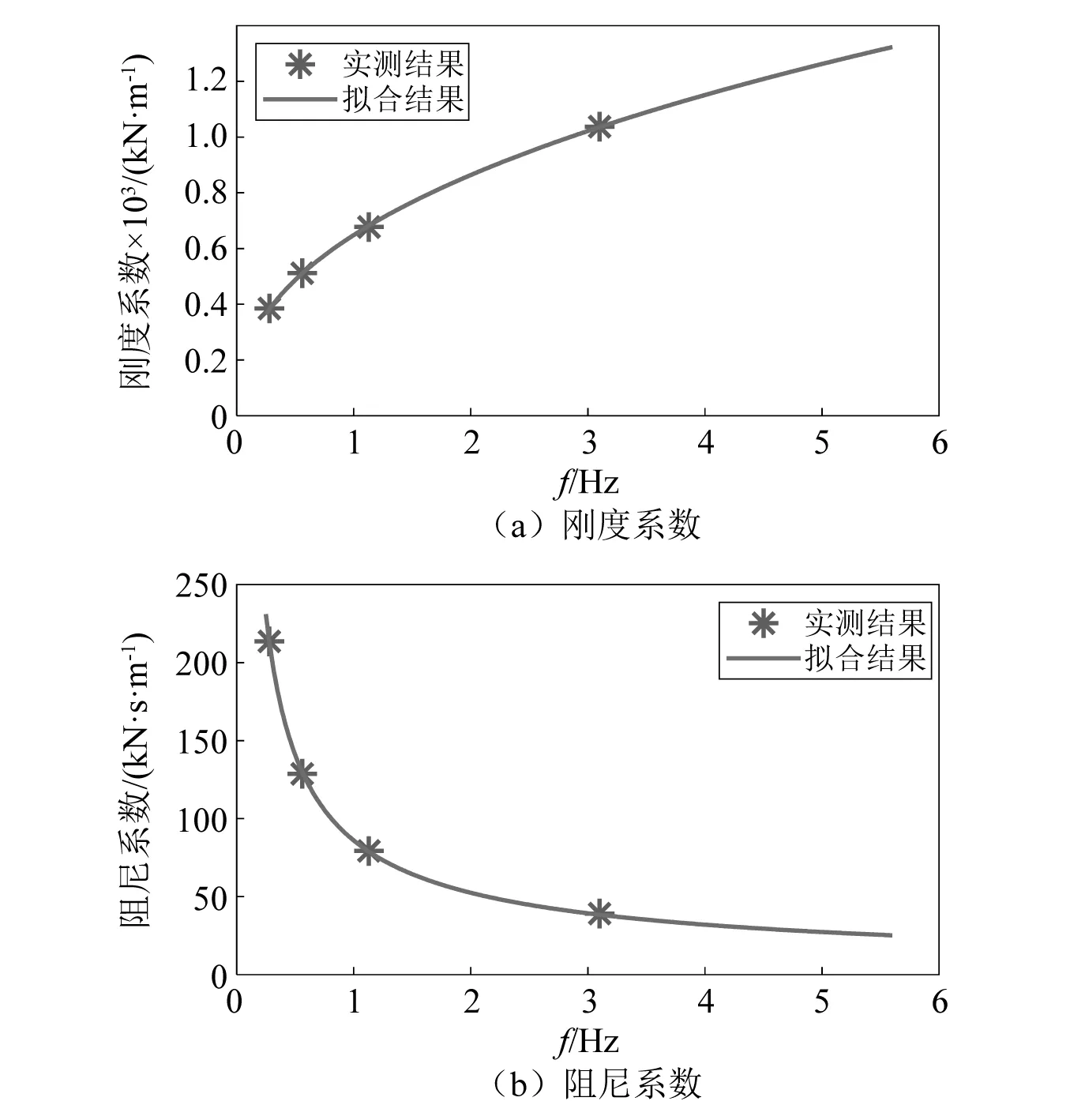
图5 阻尼器性能实测值与拟合对比Fig.5 Comparison of the identified mechanical properties and the fitting result

2 斜拉索-阻尼器系统复模态分析

采用复模态分析方法建立斜拉索-阻尼器系统的动力方程，并给出方程的求解方法，为分析阻尼器的实索减振效果奠定基础。考虑将图4所示的Kelvin-Voigt阻尼器安装在一根小垂度拉索近锚固端的位置，系统理论模型如图6所示。拉索水平放置，l为弦长，m；Le为拉索受力伸长后的长度，m；H为拉索张力，kN;m为单位长度质量,kg/m;g为重力加速度,9.81 m/s2;EA为轴向刚度，其中，E为拉索的弹性模量,GPa；A为拉索的有效截面面积，m2；kd为阻尼器刚度，kN/m;cd为阻尼系数,kN/m/s。本文关注外置阻尼器带来的附加阻尼，故其抗弯刚度和自身阻尼的影响可以忽略不计。为了描述拉索的静位移和动位移，采用图6的坐标系。以拉索弦线为x轴，y(x)和v(x,t)分别表示拉索的静位移(静止状态形状)和相对静位移的动位移。

图6 拉索-阻尼器系统模型Fig.6 A shallow cable equipped with a damper

此处系统特征方程的推导，在Krenk等[13]研究的基础上考虑了拉索的垂度效应(见图6)。有垂度拉索在距离支承点a的位置安装阻尼器，用一个横向阻尼力f(t)模拟。假设拉索为小垂度拉索，可采用垂索模型进行模拟。即，其静位移可以假定为抛物线函数

(4)

式中：d为拉索跨中垂度，m;x为拉索轴向坐标(见图6)。拉索的动位移用v(x,t)表示(见图6)，由微分方程确定

(5)

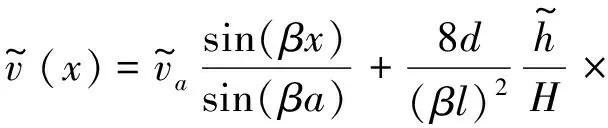
(6)

(7)

在表达式中，带波浪符的变量为时间变量的幅值。其中x′表示以远离阻尼器安装处的拉索锚固端为起点的拉索轴向坐标，阻尼器与该锚固端的距离为a′=l-a。式(6)和式(7)中波数β与拉索圆频率ω有如下关系

(8)

在频域中表示拉索弹性延伸方程，将时间函数exp(iωt)在等式两侧消去后得到

(9)

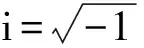
(10)

式中， 垂度系数λ2为

(11)

式中，θ为拉索的倾角，(°)。将式(6)和式(7)代入式(10)得

(12)

(13)

索在阻尼器安装位置的内力平衡条件在频域中可以表示为

(14)

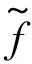
(15)

cot(βa)+cot(βa′)+

(16)

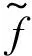
(17)

将式(17)代入(16)并简化，特征方程变为

(18)

其中，

(19)

将式(18)中的α用iη代换可以将垂索的特征方程简化成Krenk等研究中的形式。为了本文研究的整体性简要讨论了公式的推导。式(18)可以简化为类对称和类反对称模态。对于类对称模态，如式(20)所示

(20)

而对于类反对称模态可以得到

(21)

以上两式可以采用Krenk等提出的不动点迭代方法求解。

拉索第n阶模态阻尼比ζn可以通过求解复模态波数获得

ζn=I(βnl)/|βnl|

(22)

由于阻尼器靠近拉索锚固端，可以得到

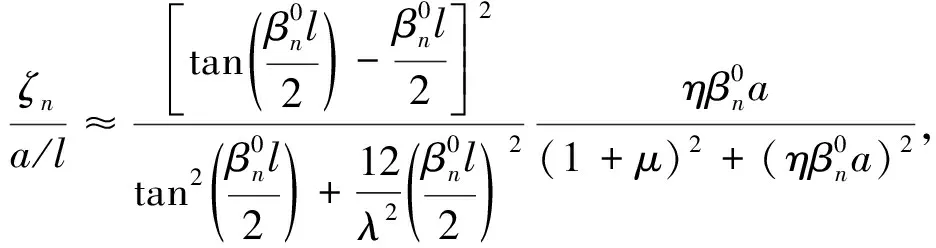
(23)

(24)

3 考虑阻尼器性能频率依存性的拉索多模态阻尼效果分析及实索验证

3.1 理论分析

采用第2章给出的复模态的分析方法，结合第2章测得的阻尼器参数，分析阻尼器对拉索的多阶模态阻尼效果。首先，根据表1所示的拉索参数得到索无阻尼器安装时拉索的第1阶～第12阶、以及第15阶和第20阶模态的振动频率，代入阻尼器力学特性的拟合函数式(3)，得到索各阶振动时，阻尼器近似的力学特性，如表2所示。然后，将表中的刚度系数和阻尼系数及对应的模态阶数代入迭代式(20)或式(21)，即可求解得到对应的模态阻尼比，如表3所示。

3.2 实索试验验证

将该阻尼器安装在目标拉索上进行实索试验，采用自由衰减实测试验方法评价阻尼器的实索多模态阻尼效果。实测试验工况可分为两组：①安装有针对设计的VSD试验组；②无外置阻尼器的对比组，目的是得到目标拉索的内阻尼。基本流程如下，根据目标模态对试验拉索进行激励，在振动幅度达到特定要求后，使拉索自由衰减，并通过其响应计算得到模态阻尼比；试验方案如图7所示。激振器、加速度计安装在桥面以上约13 m处；钢绳用于对低阶模态的人工激励。传感器、激振器和VSD的安装，如图8所示。

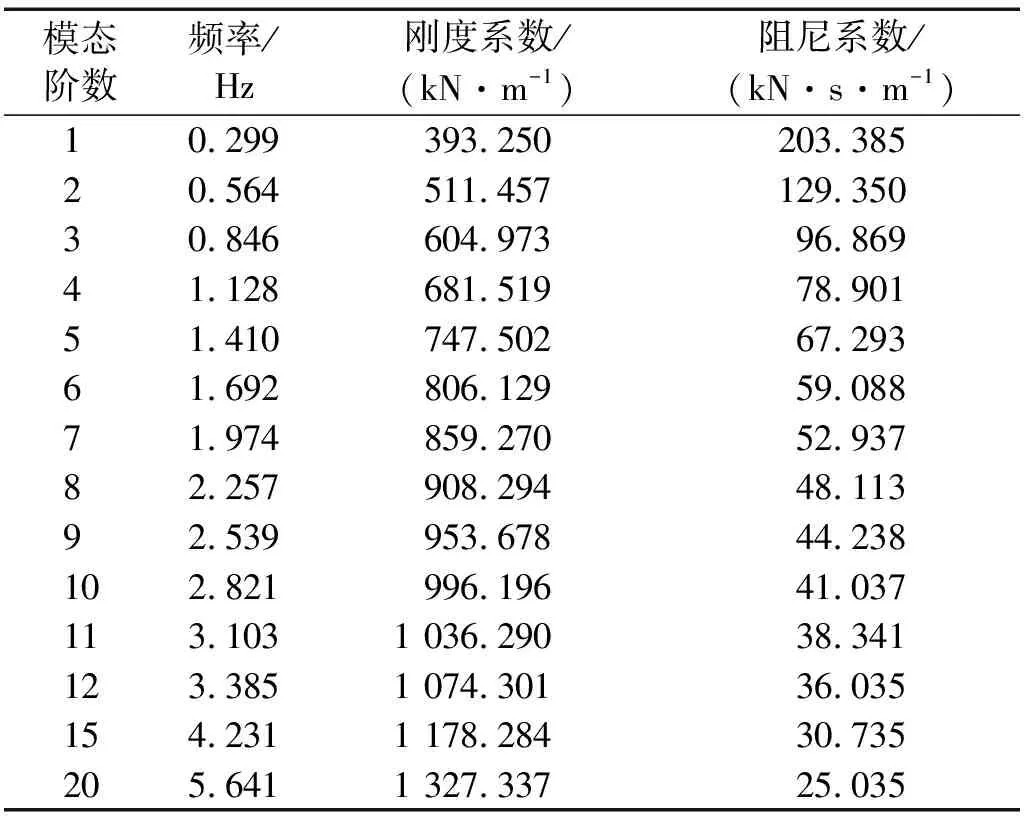
表2 基于试验结果插值得到阻尼器在不同频率情况下的刚度和阻尼系数Tab.2 Interpolation results based on the test for the stiffness and damping coefficients of the damper at different frequencies

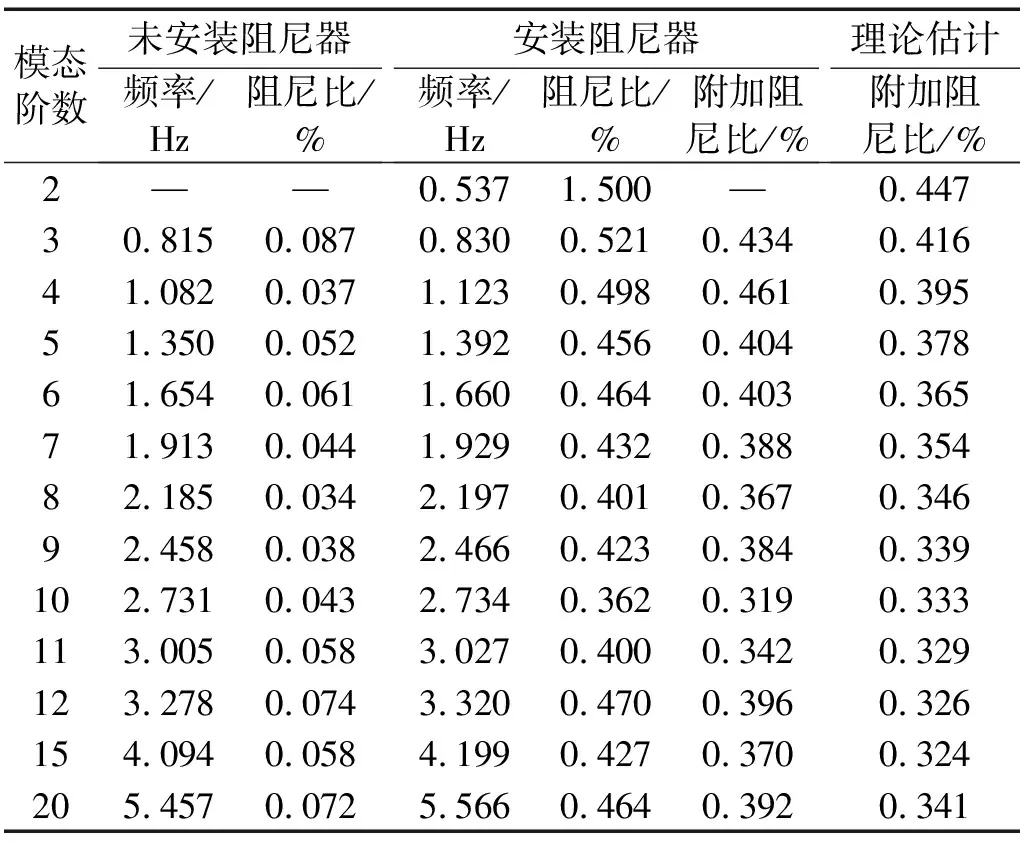
表3 示例拉索的现场实测结果Tab.3 Field test results of the example cable

图7 试验方案示意图Fig.7 Schematic diagram of field testing

图8 仪器安装照片Fig.8 Photos of installed sensors and oscillator in the field testing

现场试验中首先采用人力或者激振器对索的单阶振动进行激励，然后停止激振得到对应模态的自由衰减。实测的索单阶起振和自由衰减期间的加速度时程，如图9所示。

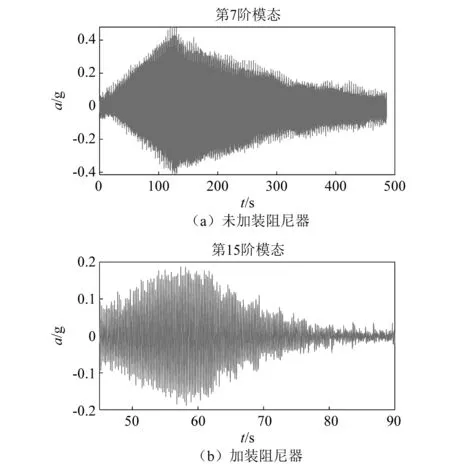
图9 实索试验加速度时程Fig.9 Acceleration time history of cable testing

然后对自由衰减部分的信号进行滤波和拟合处理，进而得到索该阶振动的模态阻尼比。以图9(b)中第15阶模态为例，信号处理的完整过程，如图10所示。

图10 信号处理过程Fig.10 Signal processing process

首先进行傅里叶频谱分析，得到拉索的模态频率，本例为第15阶(见图10(a))；然后运用巴特沃思带通滤波器在模态频率附近正负0.2 Hz区间内进行滤波处理，结果见图10(b)；然后，对滤波后时程的波峰波谷进行绝对化处理，并采用下式拟合阻尼效果：

(25)

同时，实测的模态阻尼比和根据前述的考虑阻尼器频率依存性的理论分析得到的索模态阻尼比，如图11所示。实测中，由于索激振点只能布置在索靠近梁端的位置，因此未能成功激起索的第1阶和第2阶振动。对于测试的索第3阶～第12阶、以及第15阶和第20阶振动，实测结果和理论预测较为吻合。作为对比，考虑阻尼器的刚度和阻尼系数均为定值的情况(采用单体试验第一阶结果，刚度系数384.763 kN/m，阻尼系数213.619 kN·s/m)，然后分析拉索各阶模态阻尼比，分析结果同样绘制在图11中。可见，不考虑阻尼器性能的频率依存性，理论分析会出现很大误差。

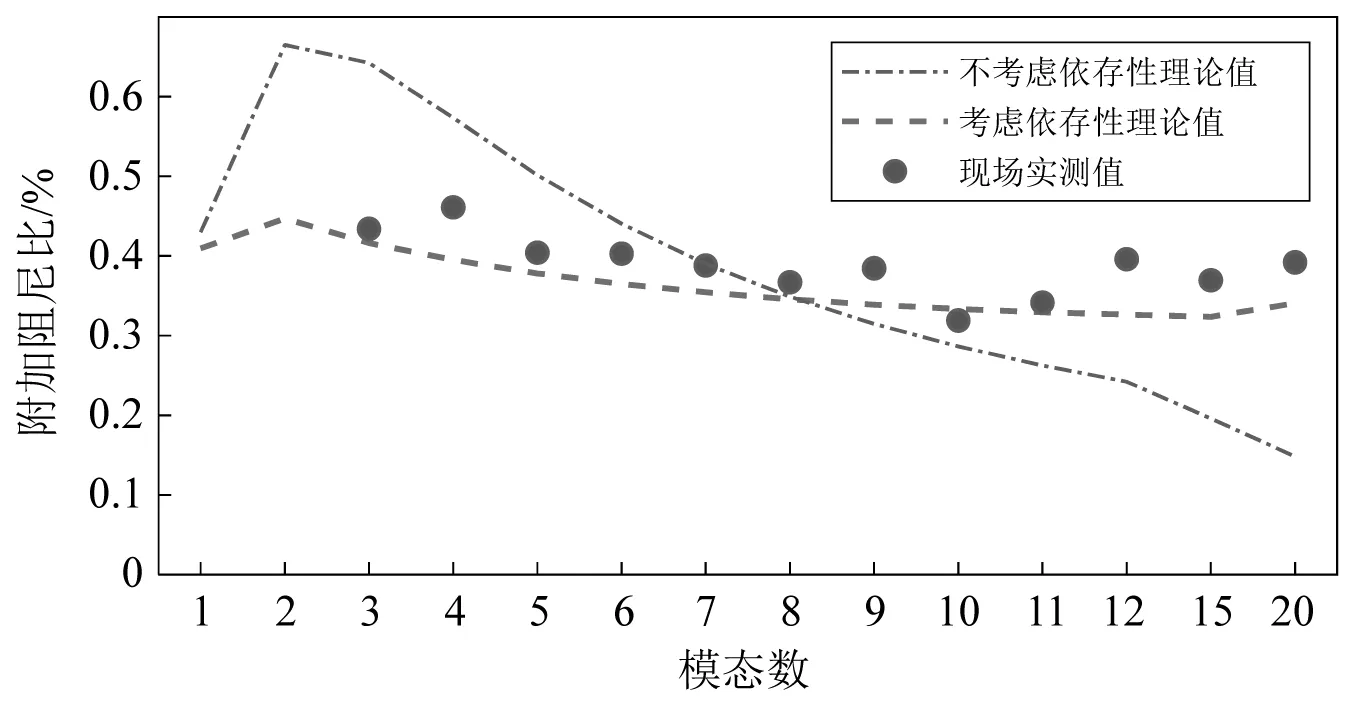
图11 考虑阻尼器参数频率依存性得到的多模态附加阻尼值与实测对比图Fig.11 Comparison of the multimode additional damping value obtained by considering the frequency dependence of the damper and the actual measurement

3.3 实用设计流程

为便于对工程减振设计的指导，根据本文研究结果，提出了一套实用的考虑阻尼器性能频率依存性的设计方法，流程如图12所示。

图12 考虑频率依存性的实用设计流程图Fig.12 Practical design flow chart considering a damper with frequency-dependent properties

4 结 论

本文以一根长454.1 m的超长斜拉索为研究对象，设计制作了一个工程中常用的VSD。首先开展了阻尼器单体性能试验，测试了阻尼器在不同频率的正弦强迫位移作用下的力学特性，结果表明阻尼器的刚度和阻尼均具有明显的频率依存性；进而，研究采用指数函数拟合试验结果得到了阻尼器特性与频率之间的近似关系。然后，研究建立了小垂度拉索附加有内刚度的阻尼器后系统的频率方程，推导了数值迭代求解表达式。最后，研究将制作的阻尼器安装在目标拉索上进行试验，测试了阻尼器对拉索10多阶模态的阻尼效果，与理论分析进行了对比和总结，可以得到如下结论：

(1) 斜拉索常用的VSD的力学特性具有显著的频率依存性，其刚度和阻尼系数与频率之间的关系可以采用指数函数来近似描述。

(2) 超长拉索振动控制需要考虑多阶模态，此时需要考虑阻尼器的频率依存性分析阻尼器对索多阶模态阻尼效果，忽略阻尼器的频率依存性会引起较大估计误差，会导致对低阶模态阻尼比的高估和对高阶模态阻尼比的低估。

(3) 基于阻尼器多频率下的单体性能试验和本文提出的索-阻尼器理论分析模型，提供了一种实用和准确的考虑阻尼器性能频率依存性的设计方法。