不确定大气分数阶混沌系统的自适应滑模同步

王春彦, 邸金红, 毛北行

(1. 郑州航空工业管理学院 智能工程学院, 郑州 450015；2. 郑州航空工业管理学院 数学学院, 郑州 450015)

目前, 混沌同步已引起人们广泛关注[1-2], 随着分数阶微积分的引入, 分数阶系统的同步研究已取得了较多成果[3-4], 由于分数阶系统比整数阶系统更贴近模型本身和实际情况, 因此在系统建模时可将系统建模为分数阶微分方程. 分数阶系统同步在生物、 化学、 医疗卫生、 通讯和物理等领域应用广泛. 由于滑模方法具有良好的鲁棒性, 因此将其引入混沌同步中, 并已取得很多研究成果[5-8], 其中： 文献[5]研究了三维分数阶混沌系统的自适应滑模同步; 文献[6]研究了分数阶高维混沌系统的滑模同步; 文献[7]研究了分数阶多混沌系统的滑模同步; 文献[8]研究了Victor-Carmen分数阶混沌系统的滑模新方法. 在实际应用中, 由于存在建模的不确定性和外部扰动, 使系统性能变差, 甚至使系统瘫痪, 因此必须考虑这些不确定因素的影响: 文献[9]研究了大气混沌系统的动力学行为与系统仿真, 对大气混沌现象进行了研究和系统描述; 文献[10]研究了分数阶大气混沌系统的比例积分滑模同步. 但利用自适应边界层理论对分数阶大气混沌系统的研究尚未见文献报道, 基于此, 本文给出分数阶滑模面的设计及控制器的构造, 从而得到大气混沌系统取得自适应滑模同步的两个充分条件.

1 主要结果

Stenflo的大气热对流混沌系统[11]可描述为

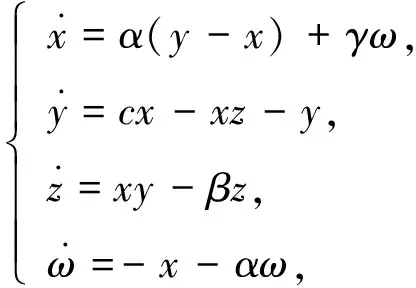
(1)

其中α,β,γ,c为常值参数, 当α=1,β=0.7,γ=1.5,c=26时, 系统(1)的混沌吸引子如图1所示.

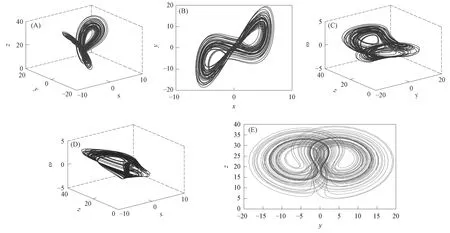
图1 系统(1)的混沌吸引子Fig.1 Chaotic attractors of system (1)

以系统(1)为主系统, 设计从系统为

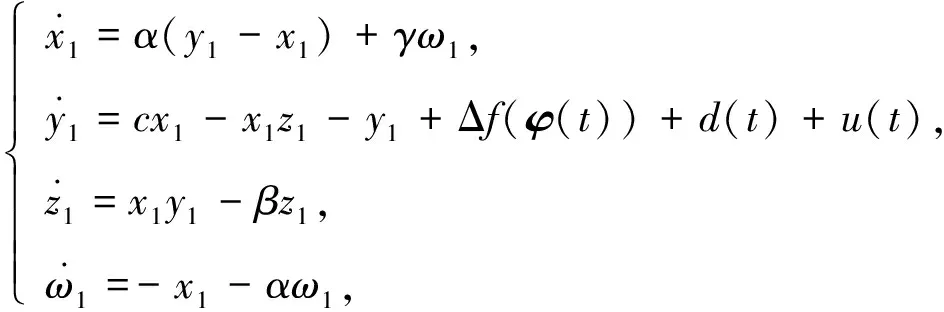
(2)

其中φ(t)=(x1,y1,z1,ω1)T, Δf(φ(t))为不确定项,d(t)为有界的外部扰动, 定义e1=x1-x,e2=y1-y,e3=z1-z,e4=ω1-ω, 可得

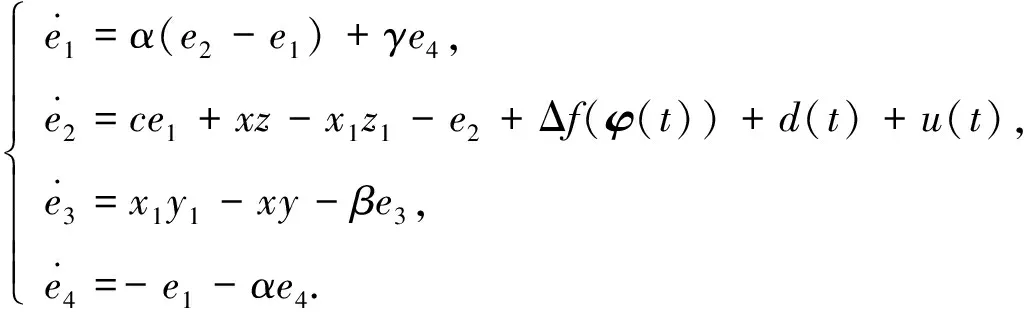
(3)

假设1设不确定项Δf(φ(t))和外部扰动d(t)有界, 即存在未知参数m,n>0, 使得|Δf(φ(t))|≤m, |d(t)|≤n.

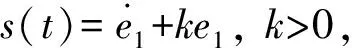
适应律为

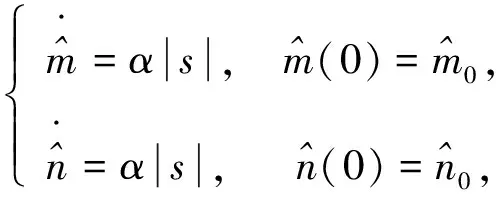
(5)

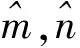
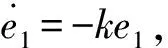
x1y1-xy=(x1y1-x1y)+(x1y-xy)=x1e2+ye1,

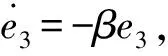
当不在滑模面上运动时, 设计

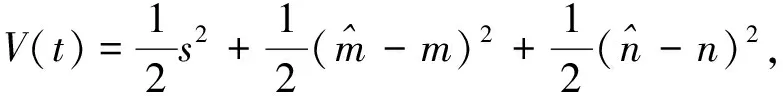
(6)

根据引理1对式(6)求分数阶导数可得

两边积分,

由引理1可得s(t)→0.

定义1[13]Caputo型分数阶微分定义为

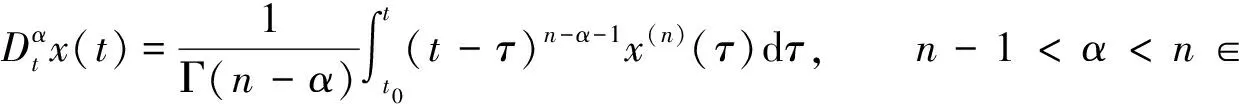
分数阶大气混沌系统[10]可描述为

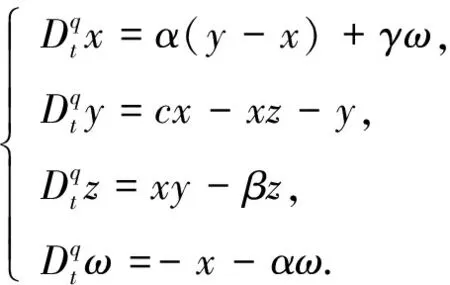
(7)

设计从系统为

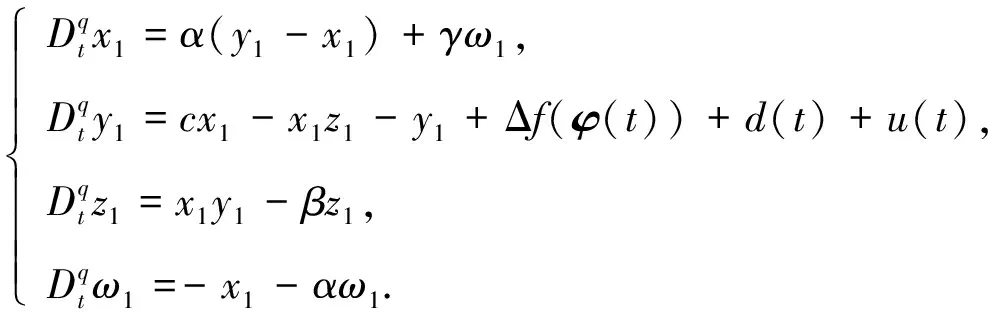
(8)

定义

e1=x1-x,e2=y1-y,e3=z1-z,e4=ω1-ω,

可得误差方程为

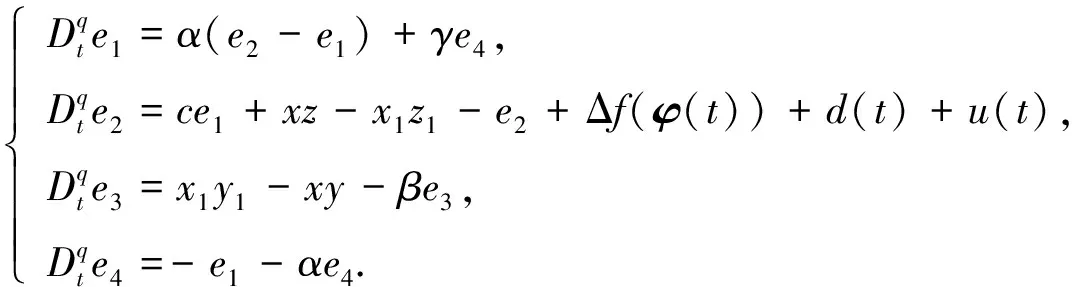
(9)

引理2[13]若x(t)为连续可微函数, 则有

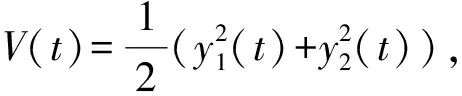
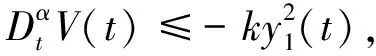
则

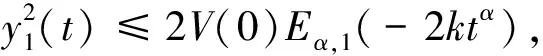
即‖y1(t)‖→0, 其中Eα,β(g)表示双参数Mittag-Leffler函数.

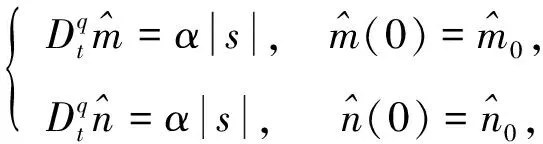
(10)

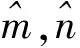
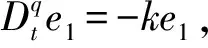
x1y1-xy=(x1y1-x1y)+(x1y-xy)=x1e2+ye1,

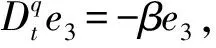
当不在滑模面上运动时, 设计

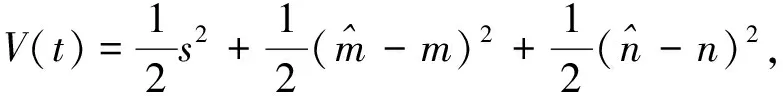
(11)

根据引理2对式(11)求分数阶导数, 可得

由引理3可得s(t)→0.

2 数值仿真

用MATLAB仿真程序进行仿真, 参数为α=1,β=0.7,γ=1.5,c=26,q=0.947,η=2, 初始值设为

(x(0),y(0),z(0),ω(0))=(3.2,8.5,3.5,2.0),

Δf(φ(t))+d(t)=0.1sin(t)x1+0.1cost,

定理1和定理2中的系统误差曲线分别如图2和图3所示.由图2和图3可见, 系统误差在初始时相差较大, 且距原点较远, 一段时间后逐渐趋近于原点, 表明大气混沌系统取得了滑模同步.该问题的解决为进一步了解和掌握大气混沌运动及气象预报具有重要作用.

图2 定理1中的系统误差曲线Fig.2 Systematic error curves of theorem 1

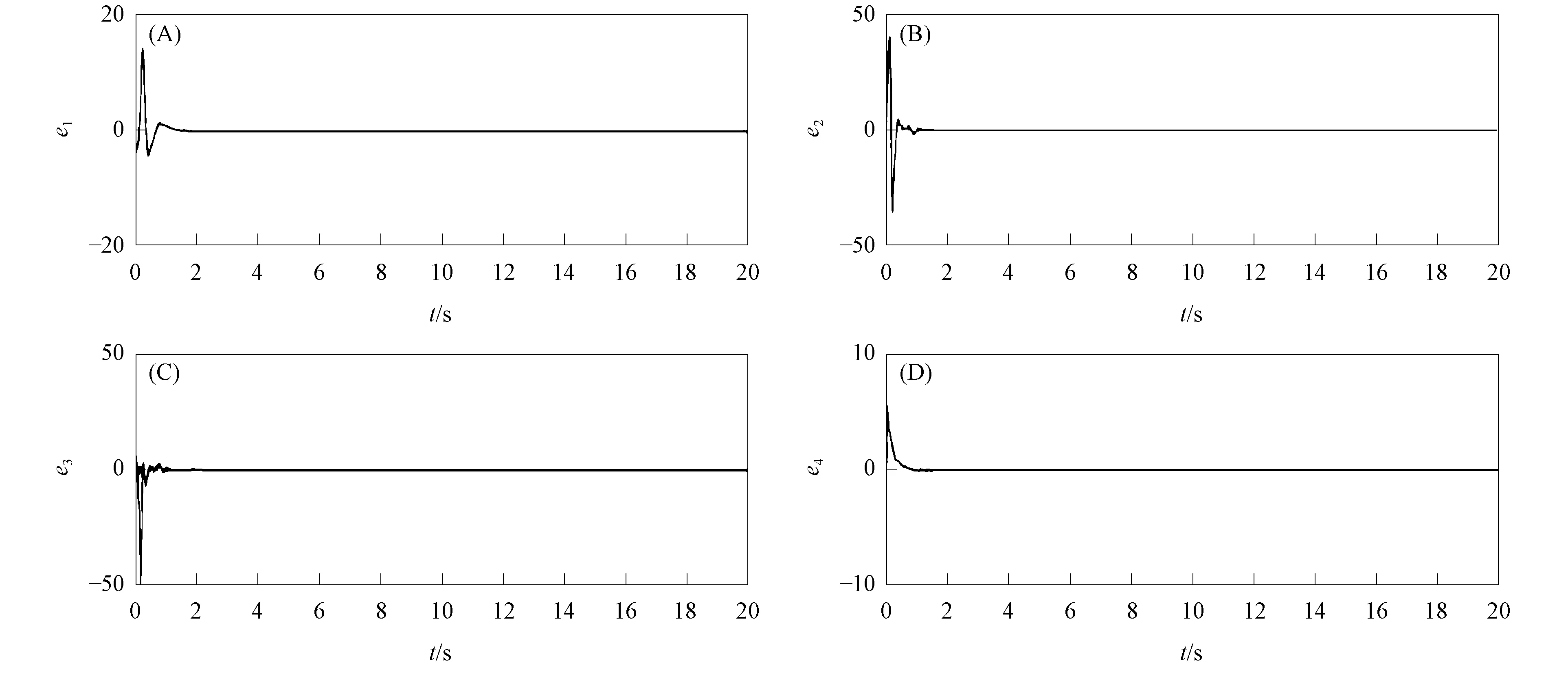
图3 定理2中的系统误差曲线Fig.3 Systematic error curves of theorem 2

综上, 本文研究了大气分数阶混沌系统的滑模同步, 利用控制理论和分数阶微分将系统建模为分数阶微分方程, 得到大气混沌系统取得自适应滑模同步的两个充分条件.结果表明, 大气混沌系统在一定的假设条件下可取得自适应滑模同步, 并将整数阶系统的结论推广到分数阶系统, 对掌握大气运行规律和大气对流气象具有一定的指导作用.