Burr Ⅻ部件相依屏蔽数据系统的可靠性分析

李 玥, 冶继民

(西安电子科技大学 数学与统计学院, 西安 710126)

在某些实际问题中, 为了解系统的失效原因和随时间变化系统的退化情况, 需要在试验的不同阶段将部分未失效系统移离试验, 即逐步截尾试验. 逐步截尾方案通常分为逐步Ⅰ型截尾方案(progressively Type-Ⅰ censored scheme, Type-Ⅰ PCS)和逐步Ⅱ型截尾方案(progressively Type-Ⅱ censored scheme, Type-Ⅱ PCS). 逐步Ⅰ型截尾是指在预先给定的间隔观察时刻点, 将预先给定数量的未失效系统移离试验, 直到试验终止时刻结束试验. 逐步Ⅱ型截尾是指每当观测到系统失效时, 将预先给定数量的未失效系统移离试验, 直到有预先给定数量的系统失效时结束试验. 逐步截尾方案比传统的Ⅰ型和Ⅱ型截尾方案更灵活, 且Type-Ⅱ PCS与Type-Ⅰ PCS相比, 可以保证至少观测到给定数量的失效系统, 从而提高试验的准确性[1-2].

系统寿命数据包括失效时间和失效原因两方面. 在工程实践中, 引起系统失效的原因多种多样, 但由于测试环境、 测试时间等因素的限制, 有时可能无法识别导致系统失效的确切部件, 而只能将其归咎于一些可能导致系统失效的部件集合. 此时, 系统的失效原因被屏蔽, 这种数据称为屏蔽数据, 相应的系统称为屏蔽数据系统. Usher等[3]采用极大似然方法研究了串联屏蔽数据系统的可靠性; Sarhan[4-5]研究了当部件寿命服从Weibull分布和Pareto分布时, 屏蔽数据系统模型的统计推断; 蔡静等[6]研究了Burr Ⅻ分布串联屏蔽数据系统的可靠性; Sarhan等[7]讨论了并联屏蔽数据系统的部件可靠性评估问题.

上述研究均假设系统部件寿命变量相互独立, 但在工程实践中, 系统部件之间通常不独立, 部件失效存在一定的相关关系. 例如, 一架双引擎飞机, 当其中一个引擎出现故障时, 另一个引擎的工作状态会发生变化, 从而维持飞机能正常飞行. 因此, 研究部件之间的相依关系及其对系统可靠性的影响有一定意义. Feizjavadian等[8]和Bai等[9]利用二元Marshall-Olkin Weibull分布描述失效原因之间的相依结构, 对相依串联系统模型进行了统计分析； Cai等[10]基于二元Marshall-Olkin Weibull分布对相依串联屏蔽数据系统进行了统计分析； 付倩娆等[11]讨论了二元Marshall-Olkin指数分布下含有屏蔽数据的相依串联系统的可靠性分析问题. 上述研究均采用多元分布刻画相依结构, 适用于系统部件寿命变量具有相同分布的结构. 但在复杂结构的情形下, 多元分布对变量之间的不对称性和尾部相依性的计算较困难. Copula函数因其灵活性可以很好地解决上述问题, 本文选择Copula函数进行相依结构的建模. Hsu等[12]基于Clayton Copula函数研究了在Ⅰ型截尾试验下多部件相依串联系统的可靠性评估问题； 蔡静等[13]基于Clayton Copula函数讨论了相依并-串联屏蔽数据系统的可靠性分析问题.

Burr Ⅻ分布[14]是一种重要的连续寿命分布. 由于其失效率函数的非单调形式, 使其适合代表许多产品的寿命, 具有很好的灵活性, 广泛应用于可靠性工程、 通信工程、 质量控制、 航空航天等领域. Burr Ⅻ分布作为一种失效模型, 关于其应用和统计性质目前已有许多研究结果. 但基于Burr Ⅻ分布对相依屏蔽数据系统的研究报道较少, 因此, 本文针对部件寿命变量服从Burr Ⅻ分布的情形, 通过引入Copula函数建立部件寿命变量之间的相依结构, 并讨论在逐步Ⅱ型截尾试验下相依串联屏蔽数据系统的可靠性. 首先, 推导出模型参数及系统可靠度函数的极大似然估计(maximum likelihood estimations, MLEs)； 然后, 基于渐近正态性理论和bootstrap抽样算法分别构造出参数的渐近置信区间(asymptotic confidence intervals, ACIs)及偏差校正的百分位bootstrap置信区间(bias-corrected percentile bootstrap confidence intervals, Boot-BCP CIs)； 最后, 用仿真模拟和真实数据分析验证所提出统计方法的可行性和有效性.

1 Copula理论

1.1 Copula函数

Copula函数是描述多元随机变量间相依结构的一种函数, 它可以将多元随机变量的联合分布函数与其边际分布函数联系起来. 下面简要介绍二元变量情形下Copula函数的基本理论[15-16].

失效Copula函数是一个多维联合分布函数, 其定义域为[0,1]×…×[0,1]. 根据Sklar定理[15], 它可以连接多个随机变量的边际分布构造联合分布. 对于二元变量的情形, 其可表示为

H(z1,z2)=C(F1(z1),F2(z2)),

(1)

二元生存Copula函数和二元失效Copula函数的关系为

1.2 相依性度量

通常的相依性度量如Spearman’sρ和Kendall’sτ都可采用Copula函数表示[15]为

1.3 Archimedean Copula族

由于Archimedean Copula族可以准确地描述非对称随机变量之间的尾相关性, 因此在实际生活中应用广泛. 二元Archimedean Copula族函数定义[15]为C(μ,ν)=φ-1(φ(μ)+φ(ν)), 其中生成函数φ(·)是一个严格单调递减的凸函数, 满足φ(μ)+φ(ν)≤φ(0),φ(1)=0,μ,ν∈[0,1],φ-1(·)是φ(·)的逆.

Clayton Copula隶属于Archimedean Copula族, 其Copula函数为

CC(μ,ν)=[μ-θ+ν-θ-1]-1/θ,θ∈[-1,∞){0}.

Clayton Copula适用于描述下尾相关、 上尾渐近独立随机变量之间的相关性, 由Kendall’sτ及相应Copula函数的关系可得τ=θ/(θ+2), 当θ→0时, 随机变量趋于相互独立.

2 模型描述和基本假设

2.1 模型描述

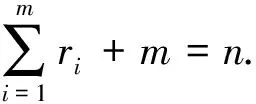
由于某些系统的失效原因并不确切, 因此用Ki(i=1,2,…,m)表示系统i可能失效原因的集合,ki是Ki的观测值.ki={1}表示系统i失效是由部件1导致的；ki={2}表示系统i失效是由部件2导致的；ki={1,2}表示系统i的失效原因被屏蔽.因此, 观测到的系统寿命数据为(t1,k1,r1),(t2,k2,r2),…,(tm,km,rm).

2.2 基本假设

1) 设Z1,Z2分别表示部件1和2的失效时间, 各部件的失效时间Zv(v=1,2)服从参数为γv,α的Burr Ⅻ分布, 简记为Zv～BX(γv,α), 其中γv>0,α>0.系统的失效时间为各部件失效时间的最小值, 即T=min{Z1,Z2}.

部件v失效时间的累积分布函数(cumulative distribution function, CDF)、 概率密度函数(probability density function, PDF)、 生存函数(survival function, SF)(也称可靠度函数)分别为

2) 假设系统由两个相依的部件串联而成, 且其失效是由最先失效的部件所致.为考察数据间的下尾相依性, 本文选择Clayton Copula刻画各部件之间的相依关系, 则系统的SF为

S(t)=SZ1,Z2(z1,z2)|(t,t)=P(Z1>t,Z2>t)=[(1+tα)γ1θ+(1+tα)γ2θ-1]-1/θ.

3) 等概率假设： 屏蔽的发生与失效原因无关, 即

P(Ki=ki|Ti=ti,Vi=v′)=P(Ki=ki|Ti=ti,Vi=v), ∀v′,v∈{1,2},

其中,Ti和Vi分别表示系统i的失效时间和确切失效原因,p≜P(Ki=ki|Ti=ti,Vi=v)表示屏蔽概率.为计算简便, 本文基于等概率假设进行讨论, 也有部分研究放宽了该假设[12,17-18].

3 极大似然估计

由部件1导致系统i失效的PDF为

由部件2导致系统i失效的PDF为

则失效系统的似然函数可表示为

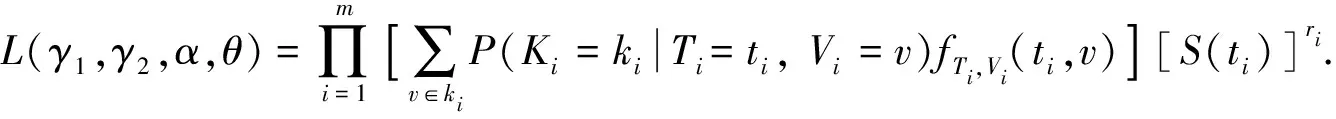
(4)

为简化似然函数, 定义失效原因示性函数为

定义辅助示性函数为

因此基于假设3), 似然函数可表示为

对数似然函数为

对lnL(γ1,γ2,α,θ)关于γ1,γ2,α,θ求一阶导数并令其等于0, 可得似然方程为

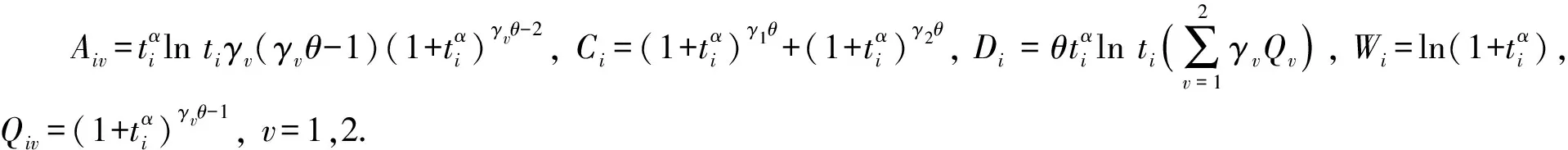
由于很难得到模型参数的显式表达式, 因此本文考虑迭代算法, 如Newton-Raphson迭代算法或其他迭代算法求解γ1,γ2,α,θ的MLEs.则系统可靠度函数的估计可表示为

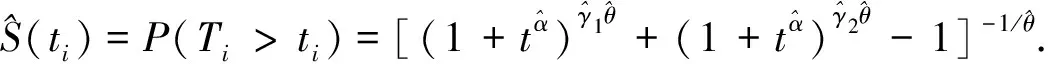
(11)

4 区间估计

4.1 渐近置信区间

记参数γ1,γ2,α,θ的Fisher信息矩阵为

其中,L(·,·)表示lnL(γ1,γ2,α,θ)对参数γ1,γ2,α,θ的二阶偏导数, 其中,

则参数γ1,γ2,α,θ的100(1-ε)%双侧ACIs为

其中Zε/2是标准正态分布的ε/2分位数.

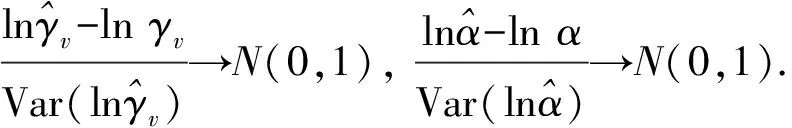
4.2 Bootstrap置信区间

在现代制造业中, 由于时间和成本的限制, 样本量通常不大, 基于大样本数据的统计方法可能并不合适, 有时甚至会产生误导. 因此, 本文采用bootstrap抽样算法构造参数的置信区间.

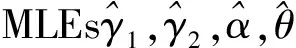
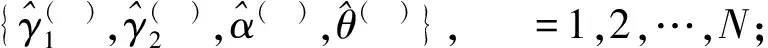
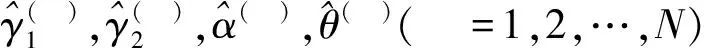
5) 参数γ1,γ2,α,θ的100(1-ε)%双侧Boot-BCP CIs为

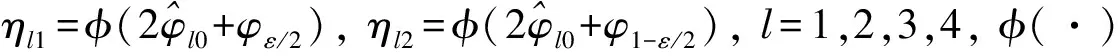
φ-1(·)是φ(·)的逆函数,I(·)表示示性函数.

5 仿真模拟

下面利用Monte Carlo仿真模拟评估上述统计方法的性能并分析模拟结果. 考虑一个具有两个相依部件的串联系统, 假设部件的寿命分布服从Burr Ⅻ分布, 利用二维Clayton Copula函数刻画其相依性. 选取参数γ1=1,γ2=1.2,α=1, 给定样本量n和失效系统数m以及截尾方案{r1=r2=…=rm-1=0,rm=n-m}, 在不同的屏蔽概率(p=0.3,0.5)和不同的相依关系(θ=2,4)下, 重复试验5 000次, 并计算各参数的MLEs、 均方误差(mean square errors, MSEs), 以及ACIs和Boot-BCP CIs的平均宽度(average widths, AWs)、 覆盖率(coverage probabilities, CPs), 结果分别列于表1～表3. 当时间t=1,2,3时系统的可靠度分别为0.347 6,0.213 4,0.152 8.

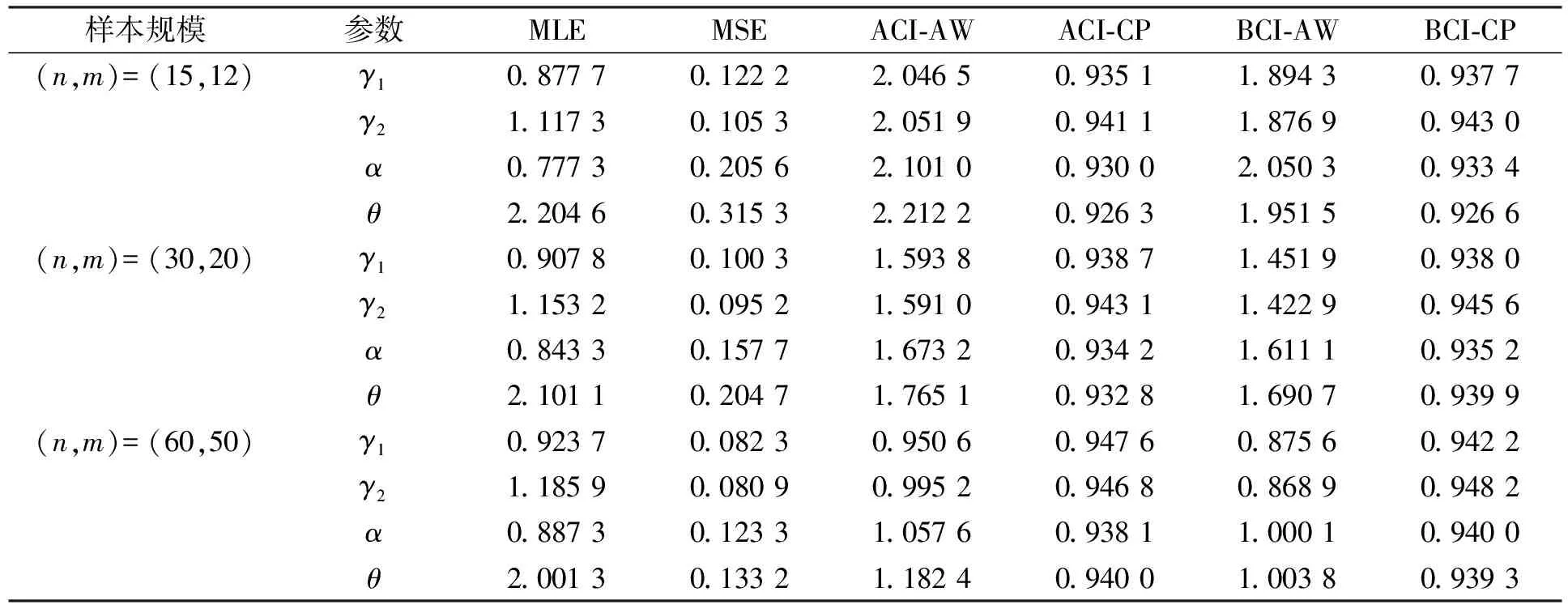
表1 当p=0.3, θ=2时, 不同样本量下模型参数的点估计和区间估计

表2 当p=0.5, θ=2时, 不同样本量下模型参数的点估计和区间估计

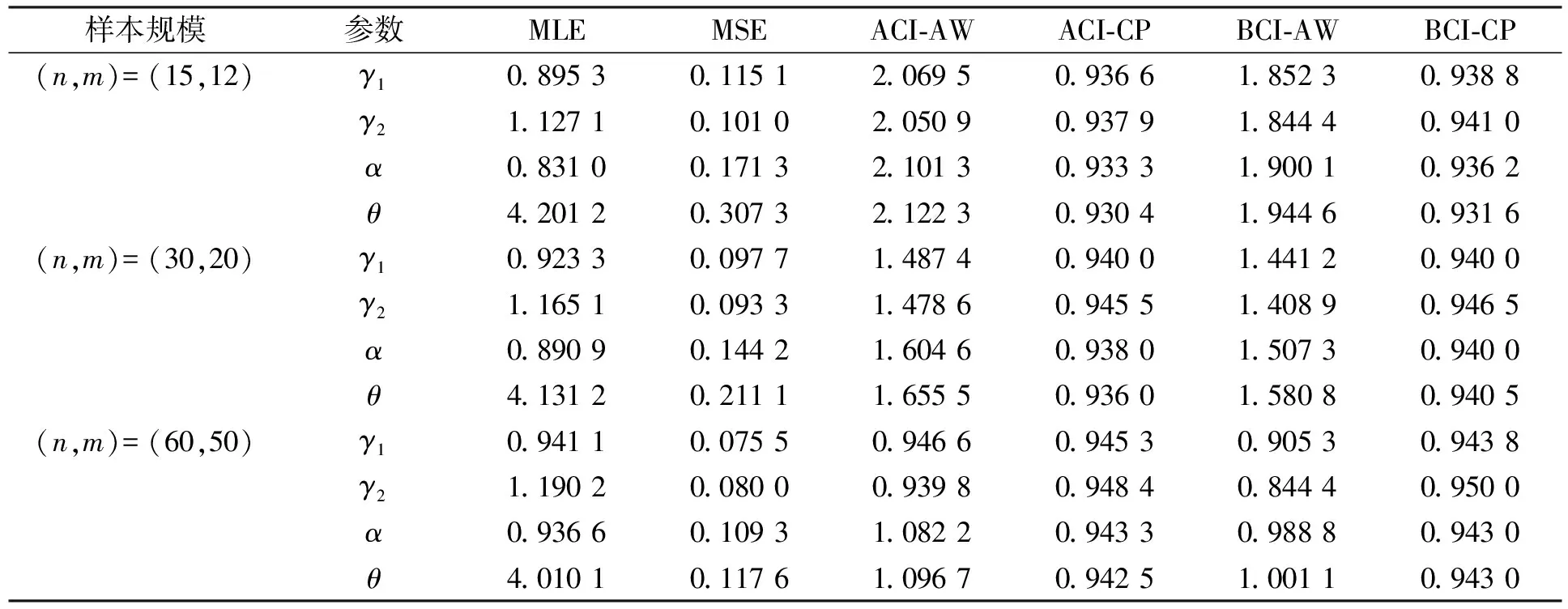
表3 当p=0.3, θ=4时, 不同样本量下模型参数的点估计和区间估计

由表1～表3可见: 随着样本量的增大, 点估计中参数的MLEs逐渐接近真值, MSEs逐渐减小； 区间估计中, ACI-AWs和BCI-AWs逐渐减小, ACI-CPs和BCI-CPs逐渐增大, 这是因为随着n或m的增加, 试验得到的有效样本量增多, 从而估计结果更准确. 随着屏蔽概率的增大, MSEs,AWs和CPs的结果表明, 参数点估计和区间估计的准确性都会降低, 这是因为屏蔽数据越多, 试验得到的有效信息越少, 因此在分析寿命数据时, 屏蔽数据的存在不可忽略. 随着部件寿命变量之间相依性的增强, 参数的MLEs接近真值, ACI-AWs,BCI-AWs都减小, ACI-CPs,BCI-CPs都增大, 表明在一定程度上考虑部件寿命变量之间的相依性是必要的.

为进一步说明屏蔽概率对系统可靠度估计的影响, 表4列出了当p=0.3和p=0.5时系统可靠度估计值以及其与真实值的误差.由表4可见, 随着样本量的增加, 系统可靠度估计值越来越接近真值.屏蔽概率的增大会导致降低系统可靠度估计的精度.

表4 当p=0.3和p=0.5时系统可靠度的比较

当p=0.5,θ=2时, 删除失效原因被屏蔽的数据, 基于失效部件明确的数据构造参数的极大似然估计, 所得结果列于表5. 对比表2和表5可见, 参数极大似然估计的MSE增大. 表明忽略屏蔽数据将导致增大参数估计的误差, 因此, 屏蔽数据的存在不可忽略.

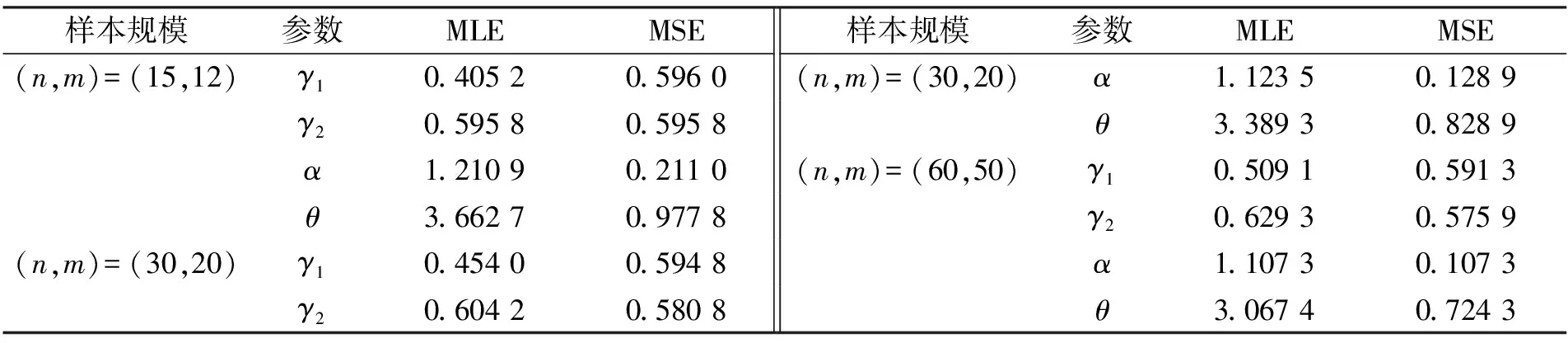
表5 当p=0.5, θ=2时, 删除屏蔽数据后模型参数的估计

6 实例分析

考虑用文献[21]中对36个小型电器进行寿命试验的实际寿命数据集验证本文方法的可行性. 在该数据集中, 失效原因被分为18种不同的模式, 观察到的大多数故障都是由模式9引起的, 因此本文将失效模式9视为失效原因1, 将其他所有失效模式视为失效原因2. 给定n=36,m=30以及截尾方案{r1=6,r2=r3=…=r30=0}, 得到含有屏蔽数据的逐步Ⅱ型截尾数据列于表6.

表6 含有屏蔽数据的逐步Ⅱ型截尾数据

基于含有屏蔽数据的逐步Ⅱ型截尾数据, 模型参数γ1,γ2,α,θ相应的MLEs,ACIs和Boot-BCP CIs列于表7. 由表7可见, ACIs和Boot-BCP CIs均包含相应的点估计, Boot-BCP CIs在区间长度上性能优于ACIs.

表7 模型参数估计

为检验本文模型的拟合优度, 采用Kolmogorov-Smirnov(K-S)检验的K-S距离和p值(表8)以及如图1所示的Quantile-Quantile(Q-Q)图说明Burr Ⅻ分布的拟合情况. 由表8可见, 当选取置信度为0.05时, 原因1和原因2的K-S距离均小于相应的临界值, 且相应的p值均大于0.05. Q-Q图也表明, 拟合的Burr Ⅻ分布是一个合适的分布. 因此, 本文提出的模型可行且有效.

表8 K-S检验

图1 Q-Q图Fig.1 Q-Q plots

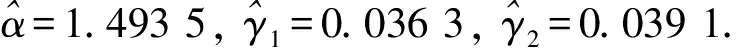
表9 Copula模型与独立模型的比较

综上所述, 本文针对部件寿命变量服从Burr Ⅻ分布的情形, 基于Clayton Copula函数, 讨论了含有屏蔽数据的相依串联系统的可靠性, 得到了模型参数及系统可靠度函数的MLEs, 并基于渐近正态性理论和bootstrap抽样算法构造了模型参数的ACIs和Boot-BCP CIs. 仿真模拟和真实数据分析验证了所提出统计方法的可行性与有效性. 在小样本情形下, 建议采用偏差校正的百分位bootstrap方法进行区间估计. 在系统寿命试验的分析中屏蔽数据的存在不可忽略, 随着屏蔽概率的增大模型参数估计的精度逐渐降低.