基于突变级数和改进AHP的系统故障状态等级确定方法

崔铁军,李莎莎

(1.辽宁工程技术大学安全科学与工程学院，辽宁 葫芦岛 125105;2.辽宁工程技术大学工商管理学院，辽宁 葫芦岛 125105)

研究系统故障过程的切入点很多，但系统故障往往是从一些事件或元件故障开始的，期间经历了各种宏观偶然、微观因果关系的变化过程，最终达到系统整体故障，丧失系统功能或功能下降。系统故障的可能原因往往难以确定，一旦系统进入故障过程将会受到各种事件、因果关系及因素的影响，将使系统故障过程千变万化，具有多样性。本文将这种系统故障过程定义为系统故障演化过程(System Fault Evolution Process，SFEP)[1-4]，其建立了从系统故障基本原因到系统故障发生过程的桥梁。在SFEP基础上研究系统故障过程的特征，需要了解引起系统故障的基本元件或事件的故障状态，了解它们在SFEP中的重要性，最终确定系统故障状态的等级。也可进一步根据系统故障状态的等级和引起系统故障的基本原因制定对应措施来阻碍系统故障的演化，这是保障系统安全可靠的重要途径之一。

目前确定系统故障过程和系统故障等级的研究方法很多，但其中大部分集中于电力、电子和电气方面的研究和应用，如双极-地制高压直流输电系统故障传递机制[5]、离网光伏发电系统故障诊断[6]、高速公路机电设备智能维护[7]、智能电能表故障预警系统[8]、电力系统风险决策的连锁故障模型[9]和弱送端系统安全稳定性分析[10]等；还有其他领域的研究和应用，如系统引发火灾概率安全评估模型[11]、利用扩展的安全失效事件网络分析铁路危险货物运输系统[12]和机着陆系统安全性能的模糊智能故障模式[13]等。另外，也有系统层面的一些方法研究，如不确定随机系统的风险评估故障树分析[14]、面向预防性维修的多状态系统可靠性模型[15]和具有多故障准则的多状态平衡系统分析[16]等。这些方法在各自领域中起到了积极的作用，为系统故障过程研究和系统故障等级的确定提供了有力支持。但SFEP包含了经历事件、影响因素、逻辑关系和演化条件等诸多要素，上述方法无论在具体领域还是系统层面方法上都难以通过故障表象找到系统故障基本原因与系统故障等级之间的关系，这给系统故障状态等级评估、系统安全分析与系统故障预防带来了较大的困难。

为了解决上述问题，本文从导致系统故障的基本原因出发，考虑系统故障过程，提出一种基于突变级数和改进层次分析法的系统故障状态等级确定方法。该方法先将系统故障过程抽象为SFEP，进而转化为空间故障树(Space Fault Tree，SFT)[17]，最终转化为经典故障树；然后在经典故障树树型结构的基础上，使用改进层次分析(Analytic Hierarchy Process,AHP)法确定各事件相对权重，再使用突变级数法确定各事件分值；最后根据改进AHP法和突变级数法确定的各事件权重和分值，确定了系统故障状态的等级。

1 系统故障演化过程描述

系统故障过程受到诸多因素的影响，内在的因素包括元件故障特性和元件组成系统的结构，外在的因素包括使元件故障特性改变的所有因素，因此描述系统故障过程至少要考虑元件故障特性、系统结构和影响因素。系统故障过程中的各种事件是相互作用的，宏观上在特定因素影响下伴有随机性地向特定系统故障发展，微观上事件间存在因果作用，从而导致了系统故障过程以网络结构形式存在。由于系统建成后元件和结构固定，其故障过程主要取决于因素影响，因此本文在文献[1]～[4]中针对因素影响，将系统故障过程定义为SFEP。SFEP由各种事件和传递组成，其中事件代表对象产生的动作和状态改变；传递代表原因(动作和状态改变对象发起的)事件导致结果事件的关系。多原因事件可以联合以某种逻辑关系导致结果事件。进一步地本文提出采用空间故障网络(Space Fault Network,SFN)来描述SFEP,进而转化为空间故障树和经典故障树，见图1。

图1(a)为设定的某SFEP的SFN。SFN由节点和有向线段(连接)组成，节点为SFEP中的事件，有向线段代表传递。其中，e1～5为边缘事件(SFEP的开始)；E1～4为过程事件；T为最终事件(SFEP的最终结果)；q1～10为传递概率，箭头方向为传递方向，表示由原因事件指向结果事件；事件下标“+”、“·”表示导致它发生的原因事件之间的“或”、“与”逻辑关系，当然还有更复杂的逻辑关系，见何华灿教授[18-19]提出的泛逻辑理论中的柔性逻辑。

图1(b)为由SFN转化得到的空间故障树(SFT)。SFN分析采取两种方式：一是SFN转化为SFT，可借助已有研究；二是SFN的结构化表示方法，有利于计算机处理。本文采用第一种分析方式得到图1(b)，图中的虚线圆代表同位事件，与被同位事件表示同一事件，只用于SFN转化后填补逻辑事件。

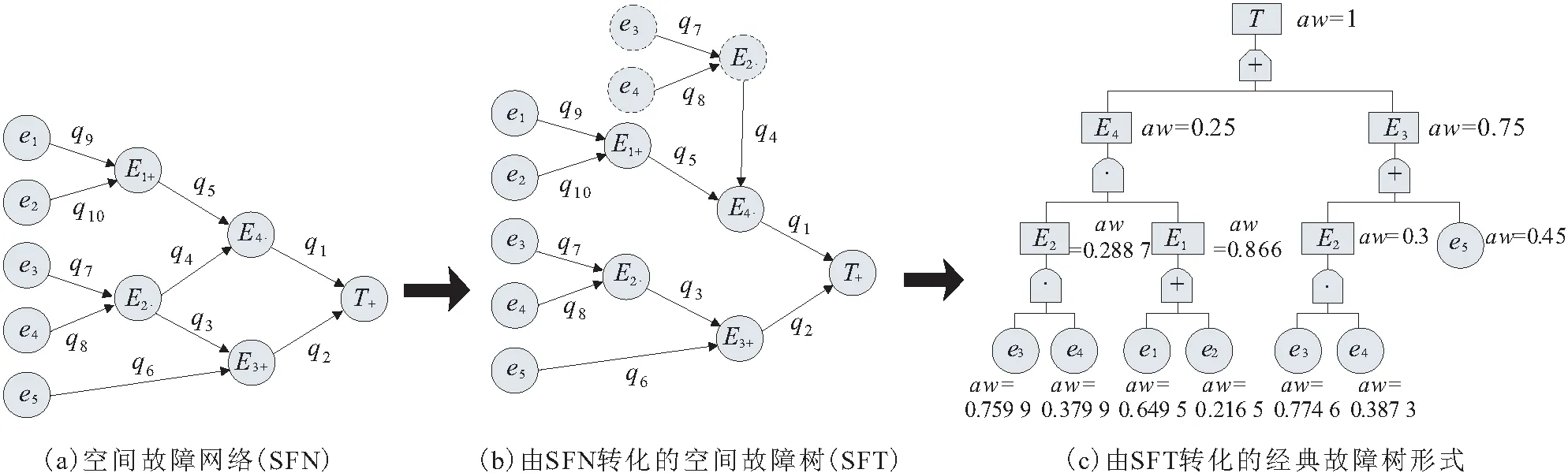
图1 某实例系统故障演化过程(SFEP)

图1(c)为应用改进AHP法和突变级数法，将SFT转化为经典故障树形式。利用该树形结构确定事件的权重和分值，而不是进行原有的定性和定量计算。

2 改进层次分析确定事件重要度

传统AHP法使用九标度进行分析，其优点是当比较对象较多时，可以详细分辨出对象之间的重要关系；缺点是当比较对象较少时，难以把握对象重要性比较的具体标度值，易造成对比结果的夸大或缩小。因此，本文针对少事件比较使用三标度进行分析，即0代表小于、1代表相等、2代表重要。同时，根据文献[20]～[22]，引入最优传递矩阵来计算判断矩阵的拟优一致性矩阵，不需要进行判断矩阵的一致性检验，使计算过程复杂度降低、速度加快且精度满足要求。采用改进AHP法确定事件权重的过程如下：

(1) 确定被分析的比较矩阵Q；

(2) 计算重要性排序指数L:

(1)

式中：i表示Q的行号；j表示Q的列号;n为Q的列数。

(3) 建立判断矩阵V:

(2)

(4) 计算最优传递矩阵H:

(3)

(5) 计算拟优一致性矩阵O:

O(i,j)=10H(i,j)

(4)

(6) 计算最大向量值和归一化的最大特征向量，得到事件权重ω:

ω=[ω1,ω2,…,ωn]

(5)

通过上述过程建立的改进AHP法，可确定由SFT转化的经典故障树同层事件的权重，并进行逐层分析，进而根据获得的同层各事件权重，再使用突变级数法按照事件权重排序对同层各事件分值进行归一化处理，得到同层各事件归一化分值。

3 突变级数法确定事件分值

突变理论是法国数学家 Rene Thom 于20世纪60年代提出的。突变理论的势函数包含两类变量，即状态变量和控制变量，它们是矛盾问题的两个方面[23-24]，控制变量决定突变类型。突变类型在理论上存在多种，但由于归一化等原因，在控制变量数超过5时，数值过小可以忽略。由于指标体系特点，控制变量数为1且状态变量数为1的情况不存在，因此本文给出控制变量数为2～5且状态变量数为1的突变类型、势函数、分支点集方程和归一化公式，见表1。

表1 各突变类型、势函数、分支点集方程和归一化公式

利用突变级数法确定同层各事件归一化分值和上层事件归一化分值的步骤如下：

(1) 确定本层事件及其分值，分值在[0,1]内。

(2) 事件数即为控制变量数，选择突变模型。

(3) 根据改进AHP法得到的事件权重排序，对各事件分值进行归一化处理。

(4) 根据互补和不互补原则计算上层事件归一化分值。

互补原则是同层事件对上层事件起相互补充作用，可取各事件归一化处理后分值的平均值[25]，对应于事件间逻辑关系的或关系。不互补原则是同层事件对上层事件不起互补作用，可取各事件归一化处理后分值的最小值，对应于事件间逻辑关系的与关系。

4 系统故障状态等级的确定

系统故障状态等级的确定方法为：首先利用SFN表示SFEP，然后转化为经典故障树；由于对比事件较少，使用改进AHP获得事件权重；使用突变级数法根据事件权重排序法，选择突变模型，归一化处理事件故障状态分值，逐层计算并最终确定系统故障状态等级。其具体步骤如下：

(1) 确定SFEP。

(2) 将SFEP转化为SFN，确定边缘事件e=[e1,…,eN]、过程事件E=[E1,…,EM]和最终事件T，以及各事件之间的逻辑关系(“+”、“·”为“或”、“与”关系)。

(3) 将SFN转化为经典故障树。

(4) 设定系统故障状态等级范围D和各边缘事件分值P=[p1,…,pN]。系统故障状态等级范围D可用下式表示：

D={[d0,d1],[d1,d2],…,[dθ-1,dθ]|d0

(6)

(5) 根据改进AHP法计算故障树中各层各边缘事件e和过程事件E的权重。

(6) 利用突变级数法对各层事件根据边缘事件评分P和重要度ω确定上层事件归一化分值。

(7) 循环上述第(5)和第(6)步骤，直到得到系统故障状态分值。

(8) 以故障树层数减1作为突变次数，使用突变系数法将原始系统故障状态等级范围D转换为D’。

(9) 当出现边缘事件在不同层时，从系统总权重1向下，根据各层事件相对权重和逻辑关系，逐层向下确定所有事件权重aw，如有重复事件则权重相加，最终得到边缘事件权重aw归一化后的权重ew。

(10) 根据边缘事件被转化的次数确定系统故障状态等级范围，并乘以这些边缘事件权重之和；同理确定其他边缘事件权重与对应系统故障状态等级范围之积，得到所有系统故障状态等级范围的交集即为系统故障状态范围;最终确定系统故障状态的等级。

5 实例分析

采用本文建立的基于突变级数和改进AHP的系统故障状态等级确定方法，对某实例的系统故障状态等级进行分析，其具体步骤如下：

(1) 使用SFN表示的实例SFEP如图1(a)所示，由SFN转化得到的SFT如图1(b)所示。

(2) 确定边缘事件e=[e1,e2,e3,e4,e5]、过程事件E=[E1,E2,E3,E4]和最终事件T。

(3) 由SFT转化得到的经典故障树如图1(c)所示，对图1(c)进行分析。

(4) 设定系统故障状态等级范围D{其中，D=[0,0.2)，表示极易故障；D=[0.2,0.4)，表示较易故障；D=[0.4,0.6)，表示一般故障；D=[0.6,0.8)，表示较少故障；D=[0.8,0.1]，表示不故障}和各边缘事件的分值P=[0.6,0.7,0.8,0.85,0.9]。

(5) 根据改进AHP法计算各边缘事件e和过程事件E的权重，计算结果见表2和表3。

表2 层次分析法权重计算的相关矩阵

表3 各事件的权重

(6) 根据表3得到的各层各事件权重，结合各边缘事件初始分值，可计算系统故障状态归一化分值，其计算结果见表4。

表4 各事件归一化分值

(7) 由表4可知，系统故障状态分值为0.969 7，但这并不是系统真实的故障状态等级。这是因为突变级数法通过小于1的变异次数计算分值，随着变异次数的增加，分值逐渐向1靠近，因此需要对原始系统故障状态等级范围D进行突变系数法转换，转换次数为树形结构层数减去1的值。

(8) 由图1(c)可知，从边缘事件到最终事件(系统故障)共有4层，则需要转换3次，转换后的故障状态等级范围见表5。进一步考虑图1(c)，e5被转换了2次，其余边缘事件被转换了3次。表4中系统故障状态分值T=0.969 7，转换2次和3次都属于极易故障状态。

表5 转换后的系统故障状态等级范围

(9) 根据系统权重1分配各事件相对权重，即图1(c)中各事件的aw值。例如：T=1，E3和E4是或关系，且相对权重为0.75和0.25，故E3和E4的权重分别为0.75和0.25；又如E4的权重为0.25，E2和E1是与关系，且相对权重为0.25和0.75，故E2和E1的权重分别为0.288 7和0.866。因此，边缘事件权重为aw=[0.649 5,0.216 5,1.534 5,0.767 2,0.45]；边缘事件权重aw归一化后的权重为ew=[0.179 5,0.059 8,0.424 2,0.212 1,0.124 4]。由于第2次和第3次转化后的系统故障状态分值均在极不安全状态，因此与各边缘事件的权重无关。

本文建立的基于突变级数和改进AHP法的系统故障状态等级确定方法的特点在于：SFN提供了故障起始原因与系统最终故障之间的关系，提供了可分析的树形结构；改进AHP法适合于对比事件较少的情况，且无需对判断矩阵进行一致性检验，能确定各事件相对权重；突变级数法根据事件权重和起始原因事件分值，逐层计算得到系统故障状态分值，并通过转换系统故障状态等级值域，最终确定系统故障状态等级。显然基于SFN的上述方法经过耦合达到了理想的效果，各方法优势互补，降低了计算量且精度满足要求，为从原因故障状态得到系统故障状态等级提供了有效方法。

6 结 论

本文建立了一种基于突变级数法和改进AHP法的系统故障状态等级确定的方法，得到主要结论如下：

(1) 空间故障网络(SFN)可作为系统故障演化过程(SFEP)分析的基础。系统故障过程用SFEP表示，SFN用于描述和研究SFEP；将SFN转换为空间故障树(SFT)，再进一步将SFT转化为经典故障树。该过程具有一定的可行性，解决了SFN分析方法存在的问题，为进一步使用突变级数法和改进AHP法创造了条件。

(2) 结合SFN，给出了突变级数法和改进AHP法的具体步骤和作用。改进AHP法适合比较事件较少的情况，无需对判断矩阵进行一致性检验，能确定各事件相对权重；突变级数法根据事件相对权重和初始原因事件分值，可计算系统故障状态分值。因此，将SFN与突变级数法和改进AHP法相结合可建立系统故障状态等级的确定方法。通过实例说明了该方法的计算过程和所得结果，验证了该方法的正确性。

虽然本文提出的方法能解决系统故障状态的等级确定问题，但由于使用了SFN对SFEP进行分析，也导致该方法存在一定的局限性：一是需要基于SFEP进行系统故障描述，进而建立SFN，这需要了解系统故障过程经历的事件、影响因素、逻辑关系和演化条件；二是在具体数据确定过程中虽然尽力避免了人为因素，但仍需要专家对数据的认可。