一种确定目标域多目标优化算法NSGA/P

马畅畅，汪 坤，鹿晓梦，陈未如

(1.沈阳化工大学 计算机科学与技术学院，辽宁 沈阳 110142；2.辽宁省化工过程工业智能化技术重点实验室，辽宁 沈阳 110142)

0 引 言

在现实工程中，会遇到一些多目标优化问题。在这类问题中，需要同时满足两个或者更多的目标要求，但是极不可能出现每个目标同时都能达到最优的情况，一个目标的改善可能会引起另一个或者几个目标指标的降低。因此，寻求绝对最优解是不现实的，但存在一个Pareto最优解集[1]。

由于进化算法能够有效解决多目标优化问题，所以通过对多目标优化问题和进化算法相结合的多目标进化算法[2](multi-objective evolutionary algorithm，MOEA)成为当下热门的研究方向。目前解决多目标问题的几大方式主要有：基于Pareto支配关系的算法[3]、基于分解的算法[4]和基于评价指标的算法，其中最经典、最具影响力的算法是MOEA/D[5]和NSGA-II(nondominated sorting genetic algorithm II)。

NSGA-II是2002年Kalyanmoy Ded等人提出的基于支配关系的多目标进化算法。随着进化算法[6]的不断发展，通过对NSGA-II与其他多目标优化算法[7]进行比较和分析，发现NSGA-II算法容易早熟，算法运行效率不够高，种群收敛性不够好并且全局搜索能力一般，尤其是在超多目标优化问题的求解上更显不足[8]。

因此一些研究人员在NSGA-II基础上提出了一些改进算法，如NSGA-III[9]，其中NSGA-II中的快速非支配排序算子、拥挤度比较算子[10]以及精英保留策略保留了下来，NSGA-III算法在精英保留策略的基础上采用参考基准的思想替换拥挤距离选取办法，能够在满足解分布的条件下解决超多目标优化问题[11-12]。

针对NSGA-II的缺欠，该文借鉴基于投影面的多目标进化算法MOEA/P[13]的投影面思想，改进NSGA-II，从而提高该算法的计算效率、收敛性与解的分布性。

1 确定目标域的多目标问题概述

以最小化问题为例，一般情况下，确定目标域的多目标优化问题(MOP with definite object domains)是求一组决策变量,使其不仅满足g、h约束条件,并且使m个目标函数在确定域内最优化，数学表达如下：

minimizeF(X)={f1(X),…,fm(X)}T

Subject toG(X)={g1(X),…,gj(X)}T,gj(X)≥0,j=1,…,J

H(X)={h1(X),…,hK(X)}T,hK(X)=0,k=1,…,K

X={x1,…,xn}T∈Ω

F∈Φ

(1)

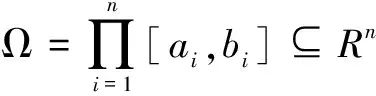
对于确定目标域的多目标优化问题求解可以采用常规MOP算法，然后在解集中选取满足目标域需求的解；也可以把目标域确定范围作为约束条件，将问题转为一般带约束的MOP。前一种方法是在全局范围内进行求解，求解效率和求解质量相对较低；第二种方法将目标与作为约束条件，大大降低了求解效率。然而，目标函数确定域作为一种特殊的约束，一定存在某种方法比常规算法有更好的性能。由于目标函数确定域的各目标函数的取值范围是指定的，所以该文提出NSGA/P算法，它可以限定种群进化方向，进一步提高算法运行效率。

2 NSGA-II算法

NSGA-II算法是在NSGA基础上做出了改进。首先父代种群Pt通过交叉变异操作生成子代种群Rt，利用快速非支配排序根据每个个体的非劣解水平对种群进行分层。先找出种群中的第一层非支配解集，并将这个解集从群体中删掉，接着找出剩下群体中第二层非支配解集，不断找出下一层非支配解集，重复这个过程，直到群体都被分层。分到同一层中的个体要根据个体拥挤距离进行排序。规模为N的父代种群和子代种群会组成一个规模为2N的新种群，根据快速非支配层及拥挤距离排序选择出N个优秀个体成为新父代。这一过程如图1所示。

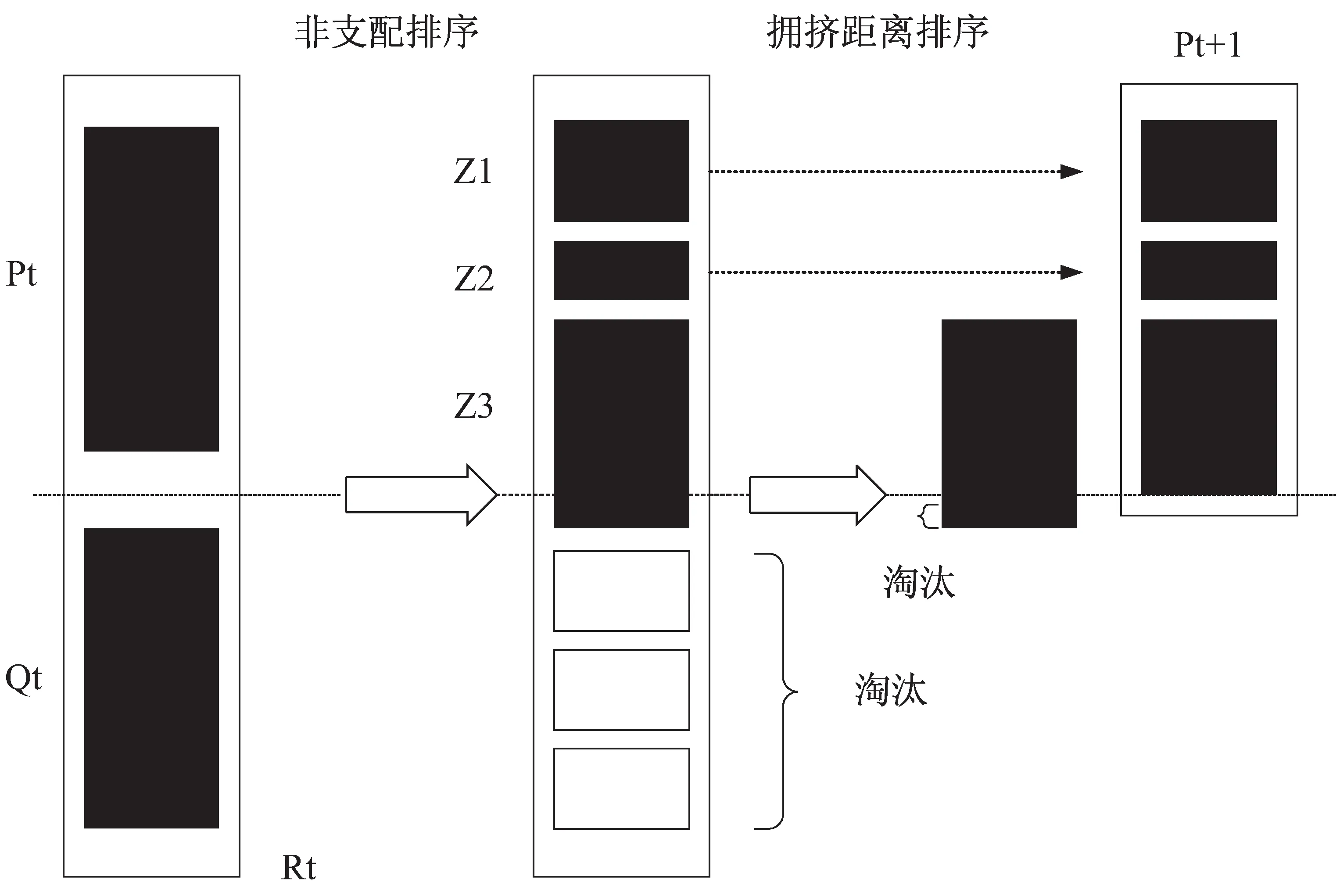
图1 NSGA-II算法过程图

NSGA-II算法通过增加精英保留策略、计算拥挤度距离和快速非支配排序策略[14]，解决了NSGA算法计算复杂度高，运行效率低，多样性和收敛性不够好等缺点。然而，由于NSGA-II算法的核心是根据支配关系进行个体的排序，在超多目标优化问题中，这种排序策略对个体的优先次序分辨度明显不足。

3 基于投影面的多目标进化算法MOEA/P

基于投影面的多目标进化算法MOEA/P可以面向目标决策支持，在指定方向上进行专门有效的求解。MOEA/P本质上采用的是基于分解的多目标进化算法思想，该算法与其他基于分解的多目标进化算法的不同之处是以降维方式将多维目标进行分解处理。它将目标空间划分为两部分：投影面和自由维，并且把投影面分割成多个投影格，然后在各个投影格上求解自由维的最优值，在求解最优值过程中，采用合适的适应度函数和空间压缩的进化算法，将种群个体压缩到投影目标空间内，从而得到多目标优化问题的最优解。这种方式既能够保证求解的精度，还能大大提高算法求解效率，又能够满足用户决策支持需求。

该文提出的确定目标域多目标优化算法NSGA/P是将NSGA-II算法与MOEA/P算法思想结合在一起。MOEA/P算法目的是对多目标优化问题进行降维处理，把目标空间分解成自由维和投影面两部分，以确定目标域为投影面，根据设置的目标域求解范围来求解最优值，采用NSGA-II算法在投影面目标域求解范围内对自由维进行相应的优化求解。这种求解方式不仅缓解了全局计算的压力，在保证求解效率的同时还保证了解集质量，又满足了用户的决策需求，从而逐步得到目标域限定下多目标优化问题的最优解。

投影面设置是NSGA/P算法主体的第一步，它将确定目标域作为一个投影面。例如在三目标优化问题上，决策者可以在第一个决策目标和第二个决策目标有期望范围，即选取前两维作为投影面，采用固定的投影格边长对投影面进行均匀分割。投影格是由相应的投影格标识向量表示，在投影格中确立求解方向，采用空间压缩进化方法，将种群进化中的个体向投影目标空间压缩，进而求出多目标优化问题的Pareto最优解。

4 NSGA/P算法框架

该文重点研究确定目标域的多目标优化算法NSGA/P。

(1)首先生成一组个体数量为N的随机种群，确定好目标域。

(2)将目标域所在的目标维组成投影面，其余维作为自由维。

(3)对投影面的根据目标域范围进行投影格分割，如图2所示。

(4)在各个投影格上，分别通过NSGA-II算法求解自由维的解集。

此处，NSGA/P算法与NSGAII算法的区别就在个体的排序上。NSGAII完全是根据个体的Pareto支配关系对个体进行排序分层，而NSGA/P同时考虑个体与投影格间的距离及个体间的支配关系。

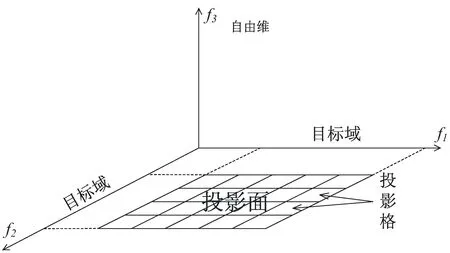
图2 目标域投影格

为此，NSGA/P算法设置两个队列。第一队列是按个体与投影格距离排序的队列。所有没有落到投影格范围内的个体在此排队；第二队列是根据Pareto支配关系及拥挤距离按NSGAII的方法进行分层排序的队列。所有落入相应投影格内的个体在此排队。进化过程中个体在这两个队列间转换，从最初的大多在第一队列逐步转移到第二队列。

(5)根据精英保留策略，每个队列都选取排序前N的个体。

(6)达到进化终止条件，整个进化过程结束，输出第二队列中当前Pareto等级最高的所有个体，即为问题求解的最优解集。

NSGA/P算法框架

输入:

·确定目标域的多目标问题MOP；

·DS:目标决策空间(投影面)设定；

·E:最大进化代数；

·N:初始种群大小。

输出:目标解集RS

过程：

步骤1：目标空间归一化。

步骤2：在投影面上求非支配解。

步骤2.1 初始化种群：

初始化大小为N的种群G，构造种群中个体并初始个体基因序列，对种群G每个个体进行初始计算，得到相应的目标函数值。保证所有个体满足MOP约束条件：如果不满足MOP，重新生成，直到G.size=N。

步骤2.2 确定目标域及投影面，并进行参考点[15-16]的选取：

根据DS确定投影面和目标域，均匀分割目标域并设置参考向量[17]。

步骤2.3 种群进化：

如果已经进化E代，或达到其他结束条件，转步骤2.4；

分别对种群G中的个体进化操作；

父子代合并后，计算个体与在最近的参考向量的距离，将该距离与个体间的支配关系组合，据此进行快速排序；

选取排序前N的个体，组成新的G。

重复步骤2.3。

步骤2.4 提交进化结果：

将G中所有非支配个体提交到RS，并保证不与RS中任何现有个体相互Pareto支配。若存在Pareto支配关系对，从RS中删去被支配的个体。

步骤3：输出RS。

5 NSGA/P算法过程图

NSGA/P算法过程图如图3所示。

6 实验及讨论

6.1 测试用例

该文选取了广泛应用的ZDT系列和DTLZ系列[18]作为测试函数，主要是ZDT1-ZDT4、ZDT6及DTLZ1-DTZL4对该算法进行测试。

通过实际最优解与真实的Pareto前沿进行对比，可以验证出NSGA/P算法的收敛性与分布性。采用Java语言，在Intel Core i5-10210U CPU @1.60 GHz环境下运行。为了简洁方便，本实验全部采用最后一维作为自由维，其余目标维构成投影面。

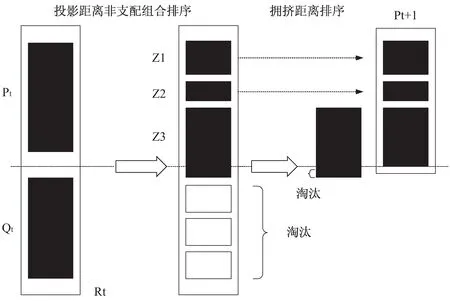
图3 NSGA/P算法过程图

对于ZDT的二目标问题，采用投影的思想将第一维设置为投影维，在确定目标域内进行实际的求解。第一维函数f1的取值设置在[0.2，0.8]这个区间，对第二维函数f2取值不约束。将实验种群大小设置为N=60，最大进化代数E=250。算法运行结果如图4所示。

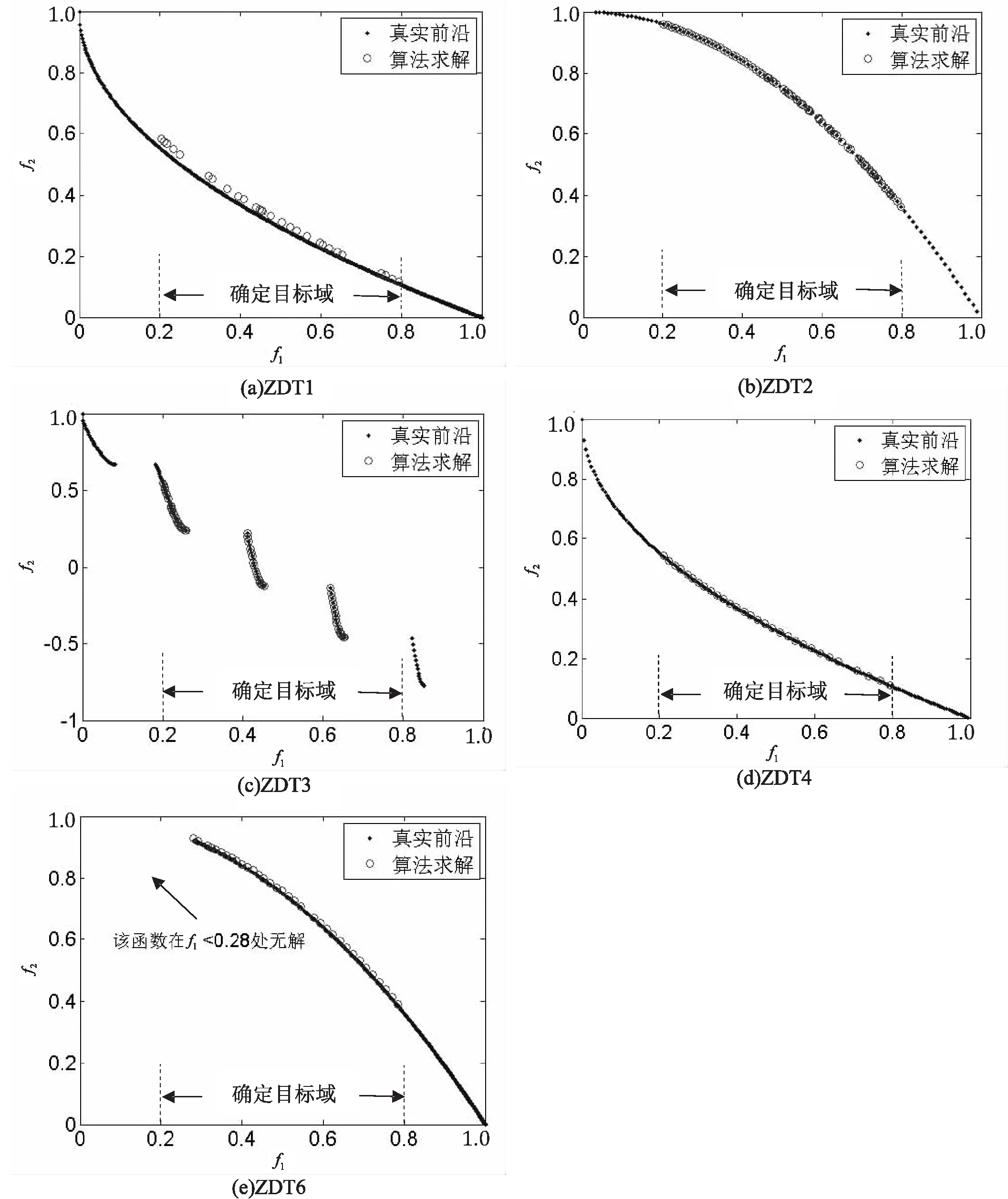
图4 NSGA/P算法对ZDT1、ZDT2、ZDT3、ZDT4、ZDT6的求解结果

通过对ZDT测试案例上的实验结果进行比较分析，得出基于投影的NSGA/P算法在确定目标域的范围内所求的最优解与真实的Pareto前沿逼近，算法收敛性效果较好，求得的最优解分布性也较好。

针对DTLZ问题，先求取三目标问题，将第一维和第二维设置为投影维，将第三维设置为自由维，接下来在投影面上进行求解。将第一维f1和第二维f2取值设置在[0.2,0.8]区间，对第三维f3取值不做约束。将实验种群大小设置为N=100，进化代数设置为E=250，运行结果如图5所示。

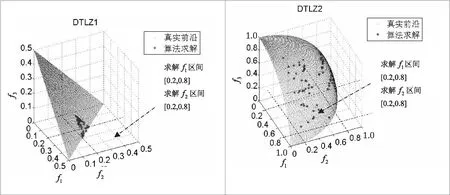
图5 NSGA/P算法对DTLZ1、DTLZ2的求解结果

通过对DTLZ测试案例上的实验结果进行比较分析，得出本算法在三维目标上也满足了求解的精度，分布性和收敛性都表现良好。

6.2 性能评价指标

为了验证算法性能，选用了CPU运行时间作为考察依据。并且选择了反向迭代距离IGD指标[19]作为评价算法的分布性和收敛性的重要依据。其中P*代表真实的PF解集，P是近似解的集合。IGD计算P*到P的平均距离公式如下：

(2)

在超多目标问题中，并且无真实Pareto前沿的情况下，NSGA/P算法借鉴了MOEA/P算法中特有的评价指标自由维误差和投影误差，使NSGA/P算法性能分析更有意义。相关指标如下：

自由维误差δd：算法求得近似解集ND中的非支配解的自由值与理想值距离的算术平均值：

(3)

其中，f和r分别表示解对应自由值和相应的理想值对应的自由维向量值，D是自由维向量数。算法所求的解与理想解越近越好。

投影误差δp：目标个体与其投影点附近所有理想值之间的平均距离：

(4)

其中，Dp是投影维个数。投影误差δp可以同时反映算法的多样性和收敛性。

6.3 算法测试结果

6.3.1 种群大小对算法性能的影响

在进化代数E=250，种群大小N在20～100范围内，目标域f1[0.2，0.8]，测试算法运行时间以及IGD评价指标结果，如表1所示。

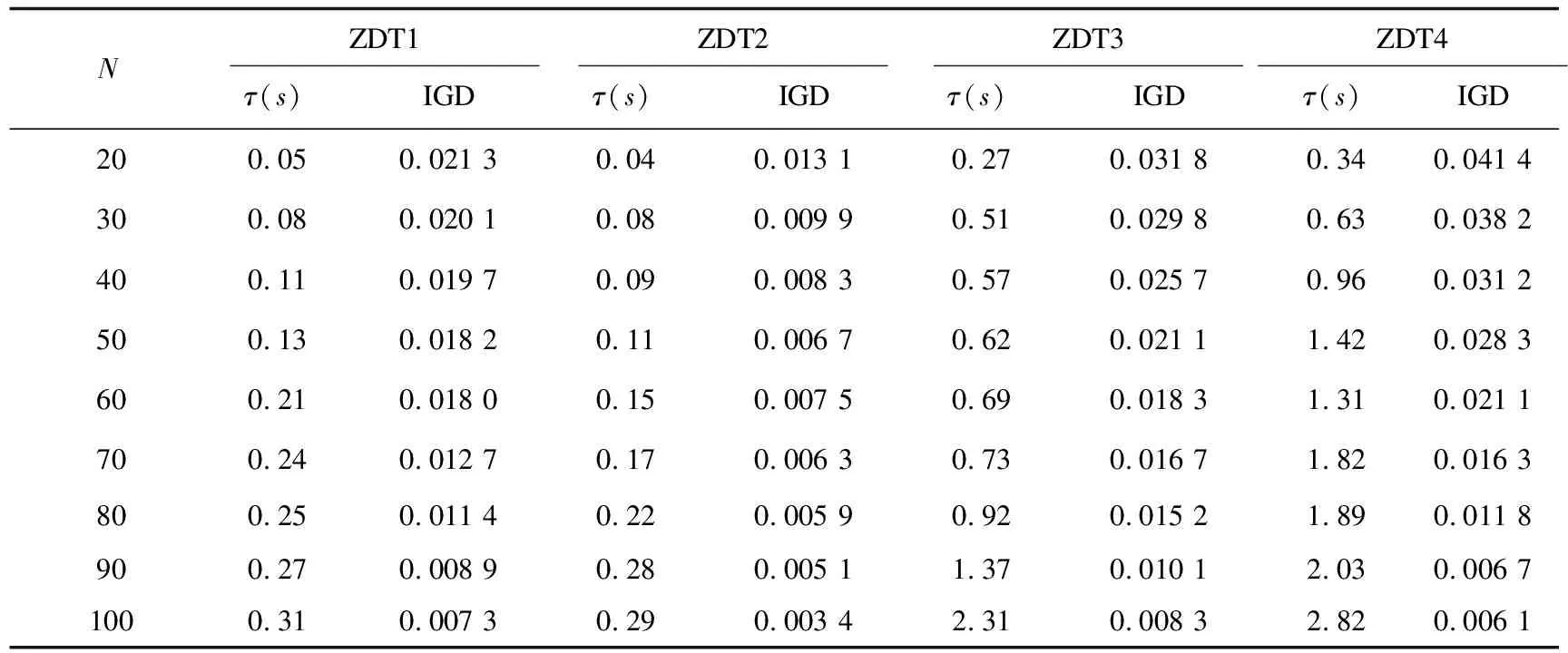
表1 种群大小对CPU时间(秒)、反向迭代距离的影响值

测试结果表明种群大小直接影响算法效率和解的质量，算法运行时间与种群大小成正比，与IGD评价指标成反比。尤其在ZDT3和ZDT4测试问题上，随着种群的增大，IGD表现得越优秀，解的分布性和收敛性越好。

6.3.2 进化代数对算法性能的影响

在进化代数E分别为50～300，种群大小N=60，目标域f1[0.2，0.8]的情况下，通过实验进行相应比较分析，测试结果如表2所示。

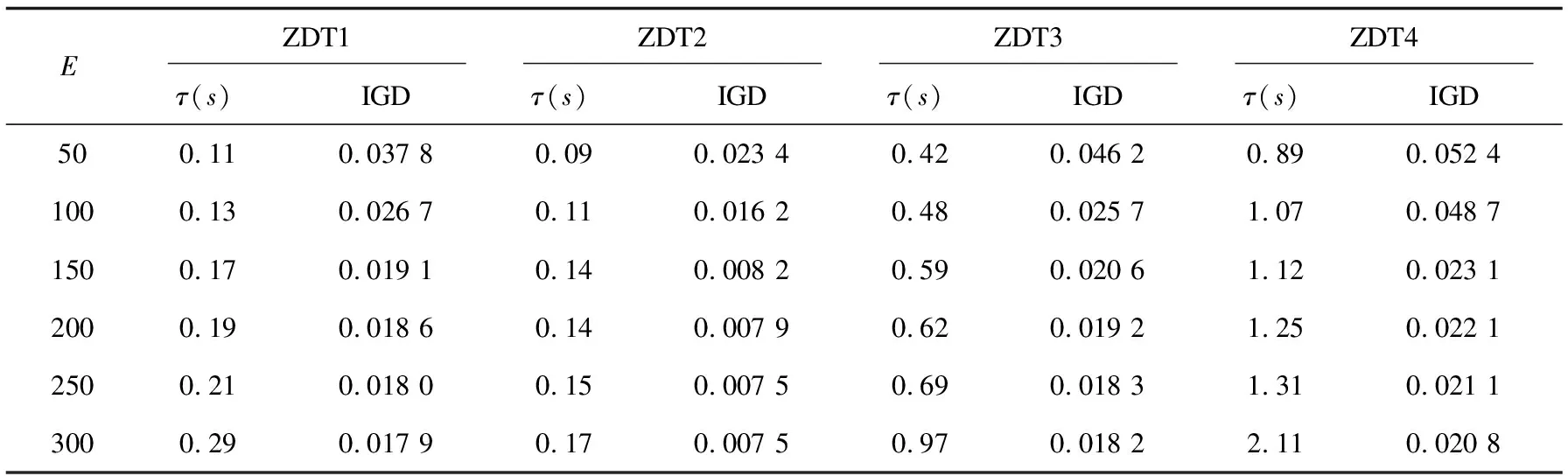
表2 进化代数对CPU时间(秒)、反向迭代距离的影响值

测试结果显示算法运行时间基本上与进化代数呈线性关系，IGD值随种群增大而减小，最后趋于一定值，并在进化到大概150代的时候，基本实现最优解的求取。

6.3.3 确定目标域范围对算法性能的影响

在种群大小N=100，进化代数E=250，不同目标域范围内进行实验。本次测试三目标问题，在f1、f2上设置同等的决策空间，分别为S1[0，1]、S2[0.1，0.9]、S3[0.2，0.8]、S4[0.3，0.7]，S5[0.4，0.6]五种范围进行测试，结果如表3所示。

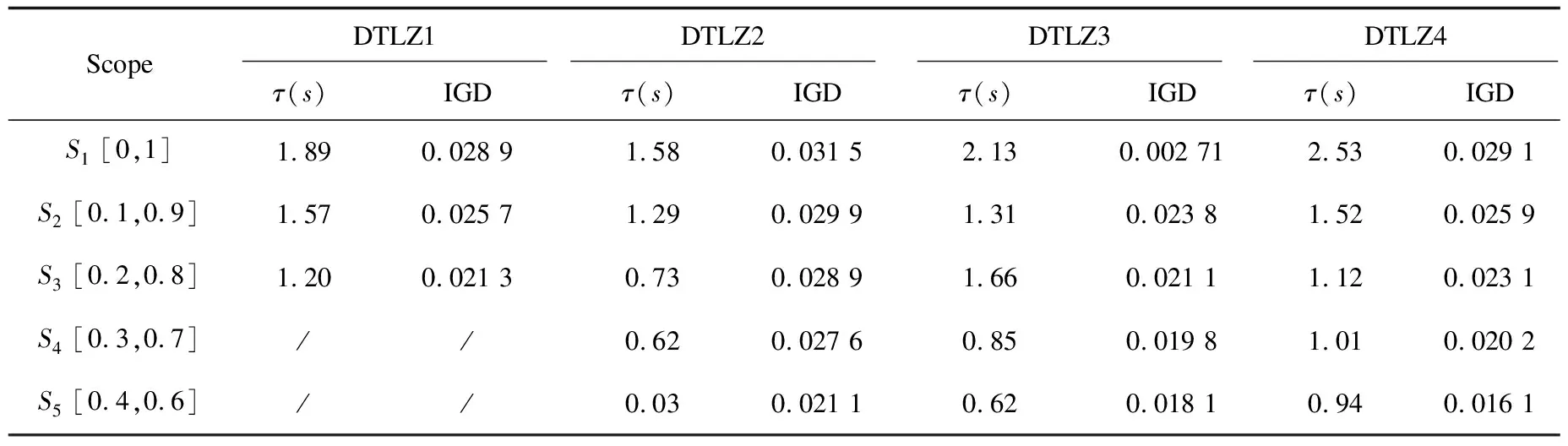
表3 目标域范围对CPU时间(秒)、反向迭代距离的影响值

实验结果表明，相同种群大小在越小的目标域内所得的最优解集质量越高(计算IGD时，在真实解集上同样选取目标域范围内的解进行计算，由于DTLZ1测试问题在S4和S5范围内取不到真实解，因此不做这两个实验)。

接下来使用测试函数DTLZ(1～4)进行超多目标实验，实验初始种群N=500，最大进化代数E=500，目标域为[0,1]。依次测试目标个数M为4到8时的最优化求解情况，每组实验均将前两维f1、f2作为投影面，剩下各维设为自由维，实验主要考察求解质量、求解效率和投影误差，全部运行10次取均值作为实验结果。实验表明随着目标个数的增加，投影误差值逐渐增大，但投影误差仍在一个较小的范围内，同时随着目标个数的增加求解时间也有所增长，这是超多目标问题下难以避免的情况。CPU时间与误差δd的运行结果如表4所示。

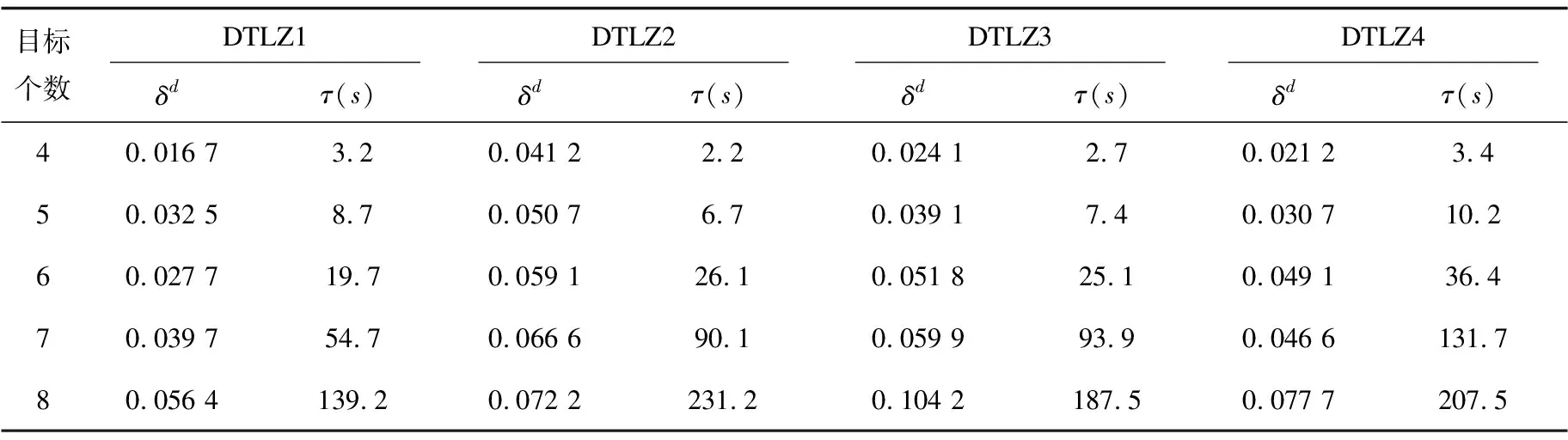
表4 超多目标优化问题解的投影误差δd值、CPU时间

6.3.4 实验对比

对比现有的一些求解超多目标算法MOEA/P，NSGA-III和MOEA/D进行超多目标问题实验，每种算法种群大小N=500，最大进化代数E=500，在目标域为[0,1]进行测试，对比实验求解的IGD值和CPU运行时间结果如表5所示。

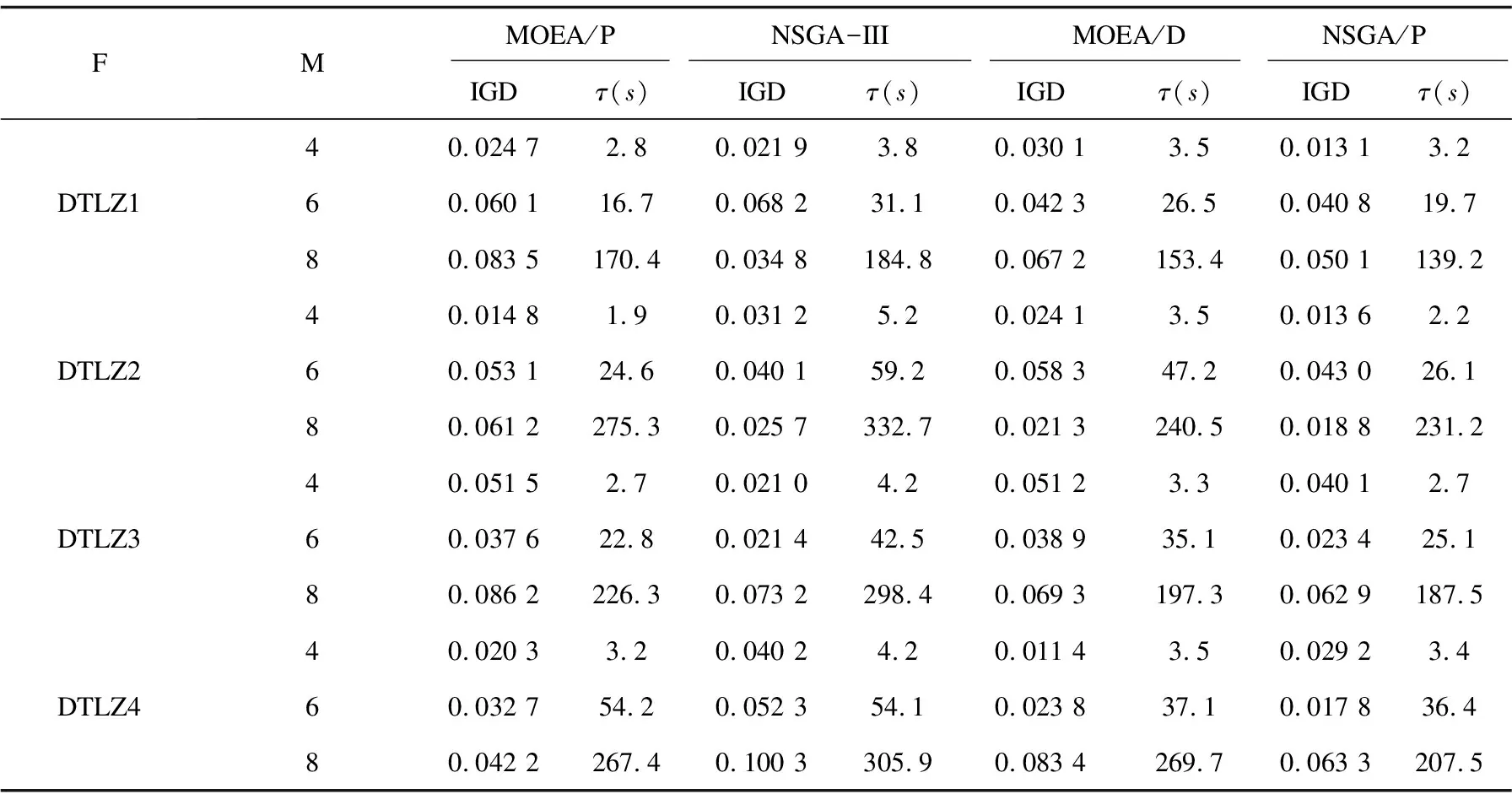
表5 超多目标算法求解IGD值、CPU时间

实验结果显示NSGA/P的求解质量普遍优于其他算法，在时间效率上也优于NSGA-III和MOEA/D，但在某些测试问题上时间效率稍微落后于MOEA/P。

通过以上实验对比发现，NSGA/P算法总体效果表现良好，具有很好的鲁棒性，适用于解决多目标优化问题，也证明了NSGA/P在求解超多目标问题的有效性。

7 结束语

通过分析并改进多目标进化算法，在NSGA-II和MOEA/P算法基础上提出了确定目标域的NSGA/P投影算法。通过对目标空间进行划分，利用降维的思想成功将高维多目标问题转化为单目标问题，再根据决策者限定的范围进行求取最优。

通过在大量的测试函数上运行算法，对实验数据进行验证及分析，所设计的NSGA/P算法有很好的收敛性和分布性，运行效率也较高，可以有效求解各种多目标优化问题，并且在求解超多目标问题上也存在一定的优势。

但NSGA/P算法同样存在不足，以后的研究方向从以下几个方面进行展开：在某些测试函数上NSGA/P的性能稍微落后于MOEA/D以及MOEA/P算法，还需要不断完善；投影后参考点的选取可能导致解的选取有很大的不同，后期应该注重参考点的选取数量以及如何设置参考点；该文根据常规的ZDT和DTLZ函数来测试NSGA/P算法，没有考虑到实际的应用问题，后期可以将该算法应用到实际的生产生活中。